问题导向 自我建构 渗透素养——以“函数复习课”为例

周 杰

(江苏省泰州市姜堰区溱潼中学，225508)

《普通高中数学课程标准(2017年版)》突出了贯穿高中数学课程的主线内容,函数作为四大主线之一,集中体现了德国数学家克莱因“函数的灵魂应该成为中学数学教学的基石”的理念．同时,新课标明确要求学生会“用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界”．那么,怎样在函数的教学中渗透数学核心素养呢?

2019年暑假期间，笔者参加了南京晓庄学院举办的“江苏省骨干教师培训班”,培训中观摩了一节“函数的复习”示范课．整节课在教师的引领下,充分发挥学生的主体性,以问题为导向,培养学生自己发现问题,提出问题,并且找到解决问题的一般方法．本文选取该节课一些教学片断,以及自己的思考与感悟整理成文,与大家交流．

一、教学片断

1.小题练习,复习回顾

课前练习:

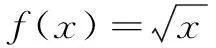
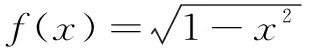
(4)函数f(x)=|x-a|的图象关于x=3对称，则a=______.

分析通过一组课前练习,达到知识或方法的回忆、识别和归类,这组练习难度低,切口小,“口答”即可解决,有利于高效归纳知识或方法,帮助学生“唤醒”知识的记忆以及掌握函数问题的通解通法．

2. 问题引导,研究函数

分析初中我们学习了一次函数、二次函数以及反比例函数．高中继续学习了指数函数、对数函数、幂函数以及三角函数等．通过回忆,让同学们认识函数贯穿了整个学习过程,同时,体会课程标准中将函数与方程作为四大主线的意义．

“对勾函数”是同学们经常遇到的函数,同学们对它的性质、图象都掌握得很好．但是,在平常教学中,很少关注它的起源．在熟悉图象、性质的基础上,反过来研究它的构造方法,不仅加深了对函数的认识,同时得到复杂函数的构造方法．

问题2我们研究这些函数的哪些方面的知识?

分析通过回忆函数的学习过程,归纳总结出函数的一般性研究方法，即函数的概念包括定义域、值域、解析式;函数的性质:单调性、奇偶性、对称性、周期性;函数的图象的作法．同时,通过引领,对函数知识进行系统归纳、总结,自主构建函数的思维导图．

分析通过学生的讨论交流,如对单个函数取绝对值没有什么意义,因为本身恒为正;又函数本身是开方形式,再开方没什么意义;取对数,函数变得更简单等,考虑这两个函数的四则运算即可．

3.变式训练,自主编题

问题4“对勾函数”是由一次函数与反比例函数相加而成,现在我们用二次函数与反比例函数组合,并尝试自主命题．

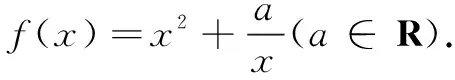
(1)判断函数的奇偶性;

(2)若f(x)在区间[2,+∞)是增函数，求实数a的取值范围.

变式题2已知二次函数y=f1(x)的图象以原点为顶点且过点(1，1)，反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8，f(x)=f1(x)+f2(x).

(1)求函数f(x)的表达式；

(2)证明：当a>3时，关于x的方程f(x)=f(a)有三个实数解.

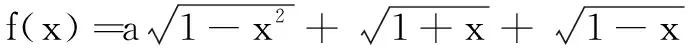
(2)求g(a).

分析通过函数组合的方式,尝试自主命题,变式题1是含参逆向问题,变式题2结合函数零点问题,变式题3是高考真题．这三道题层层递进,从不同的角度考察函数,使同学们认识到高考题来源于平时的练习中,同时养成自主学习的意识．

4.课堂小结

(1)对于给出解析式的函数,一般研究它的哪些方面?研究的思路是什么?

(2)哪些方法可以将简单函数“组合”成复杂函数?具体研究时又该如何处理?

(3)从“命题”的角度,可以提出哪些方面的问题?有什么小窍门?

(4)通过这节课的学习,你对数学(函数)学习有什么感受?

分析通过一连串的问题，包括自编的变式题,对函数知识与研究方法进行总结,帮助学生进行知识构建,形成认知结构．同时,通过课堂小结,让学生从学到会学,从做题到编题,从知识的学习升华为数学学习的情感态度与价值观．

二、教学启示

1.思维导图,纵观全局

复习是全面系统地巩固、整合知识,从而形成知识网络的重要环节．复习课不是简单地将知识点进行罗列,更不是机械地死记硬背,教师要引导学生去构建函数的知识网络结构框图．学生要将函数的思维导图构建在自己的头脑中,这样才能整体把握函数的基础知识和思想方法,有效地培养学生的逻辑思维及逻辑推理等数学核心素养,同时还可以培养和提升学生的能力．本节课通过一组小题,让学生在解题的过程中对函数知识进行回忆,对函数的方法进行归纳总结．再通过一组问题,让学生自己去构建函数的知识网络,构建思维导图．

2.问题引领,突出思想

课程标准指出,基于核心素养的教学,要特别重视情境的创设和问题的提出．在进行教学时,要树立问题意识,以问题为导向,在知识能力提升的同时,让学生形成问题意识,培养学生发现问题,提出问题,分析问题,解决问题，激发学生的兴趣,训练学生的探究意识和创新意识．本节课通过对函数的复习,归纳总结出函数的一般性研究方法,由熟悉的“对勾函数”的构造,让学生得到复杂函数一般的组合方式，从而自主编题,体会高考函数题的构造过程,养成研究函数的一般性方法的习惯．课程标准特别强调知识的通性通法,

通过简单函数的不断组合,促进学生解题思维能力的提升．

3.自主建构,渗透素养

新课程标准强调学生为本是方向,立德树人是根本,核心素养是聚焦点．数学课程必须解决好所有的人和不同的人学习数学的问题,而这一问题在高中数学课程实践中尤为重要．

本节课对函数的复习没有将函数的知识面面俱到,也没有人为地增加难度,而是在学生自主学习的基础上,以人为本,让所有的学生参与知识的构建过程,从而把握数学的本质．从学生都很熟悉的对勾函数出发,引导学生探究了复杂函数的构造方式．通过类比,让学生按照同样的方法自主编题．在编题的过程中,引入了参数、零点等问题,逐层推进,最终落脚于高考真题．通过这样的方式,不仅使学生摆脱了题海战术,增加了学习的兴趣,同时,让学生认识到高考来源于平时的学习,增加了学生学习的动力．

总之，本节课让学生自己动手,自主学习,适当引导,自主编题,提升了学生的自主意识、创新意识、反思意识、合作与分享意识．体现了课程标准中强调的教师要树立以发展学生数学学科核心素养为导向的教学意识．