完全对称式最值问题求解的“误区”*

孙 永 武瑞雪

( 江苏省睢宁高级中学，221200) (江苏省睢宁县第一中学，221200)

有一类最值问题,其条件式和待求式属于完全对称式.完全对称式指在含有n个变元x1,x2,…,xn的式子中,若将任意两个变元xi,xj(i,j=1,2,3,…,n,i≠j)交换位置后,所得结果仍与原式相同,就称该式是关于x1,x2,…,xn的完全对称式[1].这样的对称式问题在竞赛中经常出现,高考题目中也屡见不鲜.现将我校一位教师A在高三二轮复习时一堂题为“‘秒’解客观题中‘完全对称式类最值问题’”的公开课教学实录、点评与反思整理如下,以飨读者.

一、教学过程

1.开门见山，呈现案例

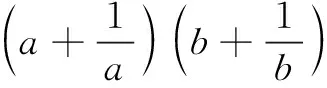
留下足够时间思考后,分别让学生板演.

师:请大家仔细检查,看看生1与生2做得对不对?

师:很好,在使用均值不等式时,一定要注意“一正、二定、三相等”的条件.生1共使用几次均值不等式?

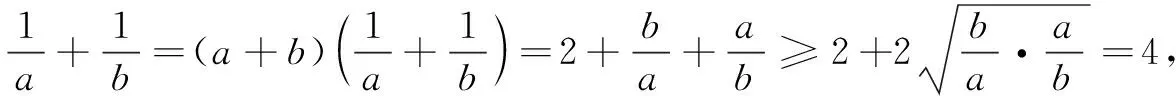
师:很好！使用“整体1代入法”可避免两次使用均值不等式.

2. 问题探究，形成规律

生4:可以,因为a=b就是等号成立条件.

生5:(立刻站起反驳)不可以,这是巧合,如果都可以,就没必要学习均值不等式了.

师:为什么会出现令a=b得到的最值与利用均值不等式得到的最值相同?这其中隐含了什么奥秘?请大家开动脑筋,大胆探索.

生6:已知等式和待求式中两个量a,b交换位置之后,没有改变.

师:把已知等式和待求式中所涉及的两个量互换位置,题目不变,这样的等式或代数式称为完全对称式,可以通过令两个量的值相等“秒”解出最值.

3. 归纳拓展，变式训练

例3若x>0,y>0,x+2y+2xy=8,则x+2y的最小值为______.

生7:令2y=t则本题是关于x,t的完全对称式,令x=t代入已知等式,即可算出x=2,因此x+2y的最小值为4.

这时就有学生感慨“太简单了”!而用“消元法”太麻烦!

师:当“求完全对称式类最值”题目出现在填空题或选择题中时,这种方法确实简单方便,但它并不能解决解答题,存在先天缺陷,所以常规的消元法、均值不等式法仍然要重点学习和掌握.通过课堂巡视,分别让生8、生9在展台上展示了两种不同的常规解法.

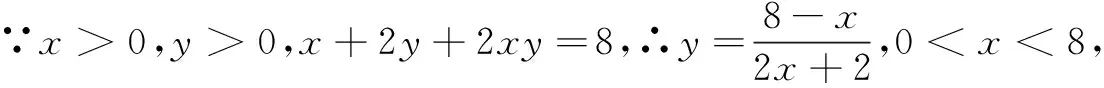
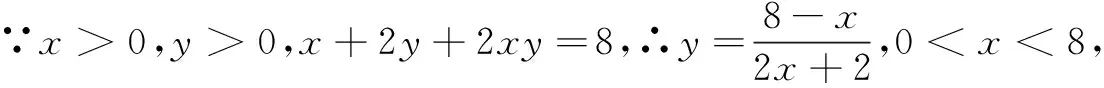
点评通过“巧法”与两种“常规方法”的对比,让学生体会到采撷优法、巧法的重要性以及“常规方法”的规范格式.

4. 部分对称，知识升华

教师A引导学生归纳得出结论:“完全对称式类最值问题能在两对称量取得相等值时求得最值.”

二、教后点评、反思

1. 难度、节奏、容量、等候时间适中

题目的难度适中,且由浅入深,讲评节奏恰到好处,题目虽不多,但把解题规律归纳概括出来,并且让学生独自探究完成.在题目出示之后均留给学生足够多的思考时间,每道题目均能讲深、讲透、讲到位,值得学习、借鉴.

2. 符合新课程标准的要求

课程标准在“学业水平考试与高考命题建议”中强调“要注重数学本质、通性通法,淡化解题技巧;融入数学文化.”[2]所以,“巧法”虽好,但教学时绝对不能忽视“通性通法”!教师A通过课堂巡视,发现生8、生9用的是常规解法,抓住时机,及时通过展台展示,通过一题多法、一法多题,培养学生思维的深刻性、发散性.

3. 对以上方法的质疑与反思

本节课主要讲解客观题中“完全对称式类最值问题”的简捷解法,那么这种解法严谨吗?通用吗?有没有例外?多思考,多深究,就会少犯错.

这一解法是错误的，其错误就在于解题过程中直接取对称的两个量x与t相等求最小值.所以,本节课归纳出的“完全对称式类最值问题能在两对称量取得相等值时求得最值”的结论,是一个“误区”,此结论只对一些“特例”适用!若教师适时强调一下“本节课所发现的结论只是对部分题目适用,在解答此类题目时,有时为了验证的需要,可以使用一下,但未必准确;若在客观题中出现此类题目,时间紧而又没有想到别的方法时,可以不妨使用此法,但也未必准确”,则更妥!