城市规模与劳动力工资议价

孔 哲，胡以文，梁欢欢

（1.中南财经政法大学公共管理学院，湖北武汉430073；2.桂林航天工业学院管理学院，广西桂林541004）

一、引言

城市规模的工资溢价是劳动经济学和区域经济学研究中一个经久不衰的话题（Rosenthal和Strange，2004）。一般来讲，影响工资水平的因素有两种：一是劳动力与雇主匹配之后的生产率水平及随之产生的经济租金，二是劳动力和雇主就经济租金分配讨价还价的结果。一些学者认为大城市汇集了更多高效率企业，通过租金分享的形式提高了雇员的工资（Au和Henderson，2006；Combes 等，2012；Combes和Gobillon，2015），还有学者认为城市规模增大会产生更多的共享、匹配和学习效果（Duranton和Puga，2004）。具体来讲，共享是指经济活动主体间共享更便利的基础设施，更大的劳动力池，更多样的中间产品，其中，包括经济风险的分担以及消费品多样化；匹配是指随着城市规模的增加，中间产品和劳动力与企业间能够更恰当地组合在一起；学习是指随着城市规模的增加引起的经济密度增加，城市人力资本外部性增加，劳动力可以从其他劳动力那里学习更多的知识，这有利于积累人力资本，企业间也会产生技术溢出从而提高生产效率。共享、匹配和学习可以降低生产成本，更好地组合生产要素，技术和人力资本外部性提高了生产效率，从而产生了更多的经济租金。目前，有关多出来的租金如何在企业和劳动力之间分配的研究甚少，随着城市规模的增加，雇主和雇员之间的租金分配会如何变化？

租金分配反映在雇主和雇员的议价结果中，一方的议价能力增强会使租金分配的比例发生改变。根据合作博弈理论，企业租金的分配结果受双方的外部机会、双方对租金的贡献度影响。城市规模增加，双方的外部选择也会增加。因为随着城市规模增加，城区内会集中更多的企业与劳动者，劳动者会搜索能提供更多薪水和更大发展前景的雇主，雇主也会搜索生产率水平更高、要价更低的劳动力。城市规模的增加使这两种活动集中在一个更密集的地区，且雇主和劳动力的选择范围大大增加，竞争更加激烈，这会对雇主和雇员之间的租金分配产生何种影响？ 目前，这一领域尚未充分研究。

研究雇主—雇员议价通常使用双边随机边界模型来测算双方的议价能力及议价结果。本文利用这一模型测算每个城市内部每个劳动力样本的议价能力，并利用匹配法比较不同规模城市相似劳动力的议价能力来分析城市规模对劳动力工资议价的影响。主要的发现：一是议价能力的分析结果显示，随着城市规模增加，议价的结果越发偏向劳动力，这符合本文的预期。二是异质性分析发现，当低技能劳动力进入等级较高的城市时其议价能力增强，而其雇主的议价能力减弱，综合作用的结果是低技能劳动力在大城市可以获得更多的企业经济剩余；对高技能劳动力来说，进入大城市固然可以使他们的议价能力增强，但大城市的雇主议价能力也增强了，综合作用的结果与小城市相比略微不利于高技能劳动力。

本文内容安排如下：第一部分为引言；第二部分从聚集效应、选择效应和补偿效应三个角度综述城市规模工资溢价的研究；第三部分介绍实证研究的思路，利用2017年流动人口动态监测数据进行实证研究；第四部分为结论。

二、文献综述

（一）城市规模与工资的关系

国外许多学者考察了城市规模与工资的关系（Glaeser和Resseger，2010；Puga，2010；Fu和Ross，2013；D’Costaa和Overman，2014），普遍认为存在城市规模工资溢价。国内相关研究也比较丰富，一种观点认为存在使工资水平最大化的最优城市规模。陈旭和陶小马（2013）、李神福（2018）、谢卫卫和曾小溪（2018）认为城市人口规模与城市职工工资水平呈倒U型非线性关系。另一种观点认为大城市存在城市规模的工资溢价。陈瑛（2018）、孟美侠等（2019）认为中国城市工资溢价主要发生在300万以上人口城市。周密等（2018）采用CHIP数据研究，发现大城市及特大城市的城市规模对农民工工资有显著影响。魏下海和董志强（2014）发现良好的商业环境可以改善工资扭曲。郑丹和Kuroda（2017）发现基础设施水平对城市居民工资收入具有溢价作用，基础设施水平对高技能劳动力溢价能力更强。大城市往往具有更好的营商环境和基础设施，因此魏下海和董志强（2014），郑丹和Kuroda（2017）的论文也可以作为城市规模工资议价的佐证。还有一种观点认为不存在城市规模的工资溢价现象。王建国和李实（2015）发现经过生活成本（以城市住房成本和省级层面物价指数来代理成活成本）调整后，实际工资在城市间并无差异。吴波等（2017）控制了人口选择效应和物价因素后发现大城市出现工资劣势。综上所述，至少就名义工资而言在大城市中存在城市规模工资溢价现象。

（二）城市规模工资溢价的解释

针对城市工资溢价有三种解释角度：劳动力选择效应、补偿效应和聚集效应。

1.选择效应

选择效应是指大城市聚集了更多的高技能劳动力，淘汰了低技能劳动力，而高技能劳动力的生产率更高，因此大城市工资更高（Bacolod 等，2009）。孟美侠等（2019）认为，大城市具有较好的公共服务和基础设施，可以提供更好的医疗和教育，这是人力资本积累的重要保障；大城市可以满足消费者尤其是高收入消费者对产品多样化、娱乐多样化的消费需求；一般来讲，个人才能报酬是随着城市人口规模递增的，这会使更有才能的人分选（sorting）到大城市中。另外，城市“内在”的技能可能存在差异，这种差异被称为“天生存在群聚”，究其原因可能是因为大城市的居民本身具有更高的技能水平。

Combes 等（2008）和Combes 等（2012）发现劳动力雇佣密度高的地区劳动力技能也更高，Berry和Glaeser（2005）利用美国的数据也得到了相同的结论。Yankow（2009）控制了劳动力可观测特征后，大城市的工资溢价为19%，当通过控制个体固定效应控制个体不可观测特征后，城市溢价变为6%，这说明大城市工资溢价中2/3 源自不可观测特征，城市工资溢价来源于某些不可观测特征的聚集。Krashinsky（2011）指出，以固定效应衡量不可观测能力存在移民小样本缺陷，作者用同卵双胞胎数据清除个人先天能力的影响，加入家庭固定效应大大降低了城市工资溢价的显著性。D’Costa和Overman（2014）发现劳动力技能分布存在较大的空间差异，控制劳动力特征使城市工资溢价剧烈下降。张国峰和王永进（2018）利用无条件分布特征—参数对应法，基于选择效应和聚集效应，综合考察了中国大城市工资溢价产生的原因，他们发现特大城市高工资和低工资劳动力并存，中等城市主要为中等技能劳动力。学者们也有不同发现，如Roca和Puga（2017）以西班牙劳动力为研究对象，通过对个体效应项进行分解，发现劳动力基于个体效应的群聚远没有之前想象的严重。

2.补偿效应

补偿效应是指由于大城市物价较高，拥挤程度较高，污染较高，从而必须支付给劳动力更高的名义工资以留住劳动力。彭树宏（2016）利用CGSS数据和工具变量法研究发现，中国100万以上人口城市存在显著的工资溢价，成因研究显示特大城市的工资溢价来源于生活成本差异。柴国俊和邓国营（2012）采用Mycos 大学生就业调查数据，用同等受教育程度的大学生数据缓解观测到的个体异质性，并将工作能力指数作为个人能力代理变量加以控制，发现生活成本有一定的解释力。李红阳和邵敏（2017）采用名义收入调整法控制城市、个体、行业因素后发现存在城市规模工资溢价，进一步研究显示，中等技能劳动者工资溢价来源于大城市更高物价的补偿效应。

此外，大城市可以提供更多、更方便的基础设施，更丰富的商品和服务，换言之，同样的购买力在大城市能获得更高的生活质量，因此人们愿意牺牲一些收入来换取在大城市居住的机会。从这个意义上讲，大城市存在负的补偿效应。

3.聚集效应

聚集效应是城市规模工资溢价研究关注的重点。聚集效应是指由于大城市稠密市场效应引发共享、匹配和学习效应，企业和劳动力的生产效率提高，导致城市规模工资溢价（Duranton和Puga，2004）。Baldwin 等（2006）、Glaeser和Resseger（2010）以及Elvery（2010）发现，大城市的企业通过知识溢出和技术进步提高了生产效率。彭树宏（2016）发现大城市的工资溢价来源于聚集效应。柴国俊和邓国营（2012）根据Mycos大学生就业调查数据，用同等受教育程度的大学生数据缓解观测到的个体异质性，并将工作能力指数作为个人能力代理变量加以控制，发现城市聚集经济是规模溢价的最重要原因。陈旭和陶小马（2013）将劳动力技能类型分为高、中、低三种类型，发现高、低技能劳动力工资溢价主要来自劳动力质量提升和大城市的聚集效应。张国峰和王永进（2018）利用无条件分布特征—参数对应法，基于选择效应和聚集效应综合考察了中国大城市工资溢价的原因，发现聚集效应占据主导地位；高工资劳动力从大城市受益更多，高工资劳动力城市间差距更明显。通常，将城市规模工资溢价效应的表现形式分为静态和动态效应（水平效应和增长效应）。静态效应来自城市规模扩大带来的运输成本的节省、中间投入品共享和劳动力共享等。劳动力来到大城市立即获得静态城市规模效应，离开大城市后城市规模效应会立即消失。动态效应主要是通过劳动力在城市的人力资本积累产生的，劳动力在大城市能积累更有价值的经验。动态效应不会随着劳动力来到大城市立即产生，也不会因为劳动力离开大城市而立即消失。

从以上论述可以看出，工资的水平效应来自大城市的共享和匹配机制，工资的增长效应来自大城市的学习效应（王建国和李实，2015）。Yankow（2009），Roca和Puga（2017）认为大城市可以为劳动力提供能积累更多高价值工作经验的机会。Baum-Snow和Pavan（2012）认为较大城市获得的经验价值甚至高于劳动力固有的能力。不少学者从学习效应引发的工资增长效应出发解释工资溢价，Duranton和Puga（2001），Moretti（2004），Glaeser和Resseger（2010）认为大城市加快了个体的人力资本积累与投资。Baum-Snow和Pavan（2012）用反事实模型估计得到城市规模工资溢价最重要的机制是对工作经验的回报不同。他们进一步研究发现，大城市与小城市之间工资差异的主要原因是工作经验报酬的差异；而在中等城市和小城市之间，工资差异的主要原因是“工资水平效应”。也有学者从共享、匹配引发的水平效应角度解释城市规模工资溢价。宁光杰（2014）发现城市规模每增大1%，工作搜寻时间减少0.124%。Meekes和Hassink（2018）发现，在共享、匹配、学习三种城市规模工资溢价机制中，共享和匹配的作用大于学习，即水平效应大于增长效应。周密等（2018）采用CHIP数据研究发现，大城市及特大城市的城市规模对农民工工资有显著影响，而中小城市的城市规模与农民工工资无关，原因是城市规模扩大有利于农民工教育—工作相匹配。

另外，也有文献认为聚集效应的作用存在群体异质性。有关城市规模的研究认为教育程度更高的劳动力从聚集经济中获益更多，而人力资本外部性研究认为较低技能劳动力因被更高教育劳动力环绕而获益更多。Gould（2007）发现高技能劳动力在城市聚集中获得的外部性收益更高。Bacolod 等（2009）发现大城市给予学习能力和交往能力较强的人更高的报酬，体力劳动者不会获得更高回报。

4.总结

通过对聚集效应研究文献的梳理可以发现，已有文献聚焦经济聚集对劳动生产率的促进作用，经济聚集通过促进劳动生产率而使工资提高。然而劳动生产率只是决定工资高低的因素之一，总产出如何在资本和劳动力之间进行分配也是影响工资水平的重要因素。因此，研究劳动力工资议价能力如何被聚集经济影响对研究城市规模与工资水平问题具有重要意义。Hirsch 等（2020）认为以往的城市规模工资溢价文献隐含了雇主向劳动力支付全部边际产品价值的假设，而没有考虑劳动力市场不完全竞争会引发雇主拥有一定程度的工资定价权。雇主的市场力量来自搜索摩擦（search frictions）、调动成本或工作差异。所有这些因素都有可能影响劳动力对工资水平的反应，从而导致单个公司的劳动力供给曲线向上倾斜。这使得雇员只能获得边际生产力的一部分作为工资，这一部分的大小取决于雇主在劳动力市场中的垄断权力（Combes和Gobillon，2015）。而雇主的本地垄断权受到当地市场密度的影响，更厚的劳动力市场竞争更激烈（Manning，2010；Hirsch 等，2013），更厚的劳动力市场中劳动力会获得更大的边际生产力份额。大城市劳动力—工资水平的匹配更有效，劳动力更容易更换雇主，大城市不仅可以提高匹配的平均质量，而且可以在任何特定匹配中为劳动力提供更多的市场选择。这表明在众多雇主竞争激烈的劳动力市场中，雇主市场支配力的三个来源发挥的作用可能较小，因此可以预期，就算没有城市规模引发的学习效应，仍能看到存在城市规模工资溢价（Hirsch 等，2020）。Manning（2010）和Hirsch 等（2020）强调，随着经济聚集的增加，雇主在劳动力市场的力量如何变化从而影响工资，但他们的模型建立在雇主定价的假设之上，通过分析雇主面临的劳动力供给曲线弹性随城市规模变化决定雇主的最优工资定价，从而决定劳动力获得其边际收益产品的比重。

通过文献梳理可以发现，现有文献尚未涉及城市规模与劳资分配的研究，更缺乏基于劳资工资议价框架的城市规模与劳资分配的研究，本文尝试填补这一空白。

三、实证分析

（一）研究思路

本文沿着Hirsch 等（2020）的思路，引入劳动力工资讨价还价模型，实证检验中国100万人口以上规模城市的城市规模与劳动力工资议价能力之间的关系，以期对中国城市规模工资溢价作出新的解释。通过构造双边随机边界模型，利用2017年流动人口抽样调查数据的大样本优势对46个城市的市辖区样本逐一进行双边随机边界计算。之所以要对46个城市的样本进行逐一回归是考虑到每个城市的补偿效应和聚集效应不同，对每个城市工资决定机制的影响也不相同。根据双边随机边界模型的性质，实际工资可以分解为三部分：一是市场中该劳动力的“公允工资”水平（以回归方程来体现），二是劳资议价对工资水平的影响（以向上的残差和向下的残差体现），三是随机因素对工资水平的影响（以第三个残差体现）。MLE 估计得到的工资决定方程是资本和劳动议价能力势均力敌时的“公允工资”，而不同城市的工资回归方程所表示的“公允工资”体现劳动者所在城市的生活成本和教育报酬率（如果一个城市生活成本高和教育报酬率高，那么该城市的工资回归方程中的截距项和教育系数肯定要更大）。分城市回归的好处是由聚集效应和补偿效应造成的大城市劳动力名义工资的提高被 “吸收” 进不同城市回归方程的截距项和斜率之中，从而避免被“吸收”进模型的两个衡量议价能力的残差之中，避免了补偿效应和聚集效应对议价能力度量的影响。如果采取统一回归的方式，所有的城市样本产生一个基准方程，那么城市间补偿效应和聚集效应的不同所造成的工资水平差异无法体现在不同的截距项和斜率项中，因此肯定会被“吸收”进度量议价能力的残差之中，从而影响议价能力的正确度量。所以，分城市回归可以排除补偿效应和集聚效应的干扰得到议价效应。计算得到各个城市每个劳动力的议价结果后借鉴孟美侠等（2019）的思路，运用匹配法对不同规模等级的城市样本进行两两匹配，从而缓解不同规模城市内劳动力属性的分布不同即选择效应的影响，至此影响议价能力计算的三个效应都得到了缓解，可以体现相对精确的城市规模与劳动力议价能力的关系。

（二）模型构建

假定在一个典型的不完全竞争的劳动力市场中，雇主和员工都具备一定的讨价还价能力。劳动力工资的最终定价（W）可表述为如下形式：

其中，W为雇员所可能接受的最低工资水平，W为雇主所愿意支付的最高工资水平。η（0≤η≤1）用于衡量雇主在定价过程中的议价能力，因此，反映了员工所得的剩余。

为了在模型中同时体现雇主和员工在定价过程中的议价能力，先描述在个体基本特征x条件下的“公正”工资水平μ（x）=E（θ|x），这里θ是实际存在的，但是无法获知，并且总满足：≤μ（x）≤。因此[μ（x）]代表工资讨价还价中雇主所获得的剩余；[μ（x）-]代表员工所获得的剩余。哪一方能够“掠取”更多的剩余依赖于他们所具有的讨价还价能力和占有信息的程度。据此，我们可以重新表述为：

定价方程式由三个不同部分组成：第一部分μ（x）表示在给定个体特征x的情况下的预期工资，我们称之为基准工资；第二部分体现了雇主的预期剩余；第三部分是员工的预期剩余。净剩余NS=η[μ（x）]-（1-η）[μ（x）-]可用来描述工资形成过程中议价能力的综合效应。

该模型是一个典型的双边随机前沿模型（Kumbhakar和Parmeter，2009）。其中，μ（xi）=xi′β，β为待估计的参数向量，xi为样本的个体特征；wi=ηi[μ（xi）]≥0；ui=（1-ηi）[μ（xi）]≥0；vi为一般意义上的随机干扰项。员工可以通过掠取雇主的剩余部分来提高工资水平，这可以通过wi体现，而雇主则可以通过掠取一部分员工剩余来降低所支付的工资水平，由ui描述。而这些掠取所得剩余的规模取决于主体议价能力η、雇主预期剩余和员工预期剩余μ（x）。

因为要对每个城市逐一进行计算，故需要拥有大量个体样本量的数据库，2017年流动人口调查数据拥有样本量大、时间较近，包含较详细的就业和地址信息的优势，所以采用该数据库。城市规模的聚集效应主要体现在市辖区的高密度聚集，而不是周边县市区，所以只保留市辖区样本。采用2017年流动人口动态调查数据与各县级行政单位代码相匹配后删除周边县市区样本，仅保留市辖区在业劳动力样本。因为在公共部门工作的人口不存在与政府部门讨价还价的可能性，因此删除在公共部门就业的样本。因更换雇主造成讨价还价对象改变或兼职其他工作易造成工资计算不准确，故仅保留单一雇主没有切换工作的样本。因模型收敛需要一定的样本量，故删去样本量较少的中小城市，保留市辖区样本量不低于200个的城市。最终保留劳动力个体37343个，涉及46个城市。为了计算每个劳动力的议价能力，需要选取工资变量和影响工资的变量，我们选取学历（考虑到受教育程度的非线性影响）、性别、劳动力市场经验、工作经验、是否农业户口（农业户口为1，非农业户口为0）、婚姻状况（已婚为1，未婚为0）、是否党员（党员为1，非党员为0）、是否签订劳动合同（未签订劳动合同为1，签订劳动合同为0）、是否垄断行业（垄断行业为1，非垄断行业为0）作为自变量，工资的自然对数作为因变量，相关变量的描述性统计如表1所示。

表1 变量描述性统计

（三）模型筛选

建立双边随机前沿模型如下：

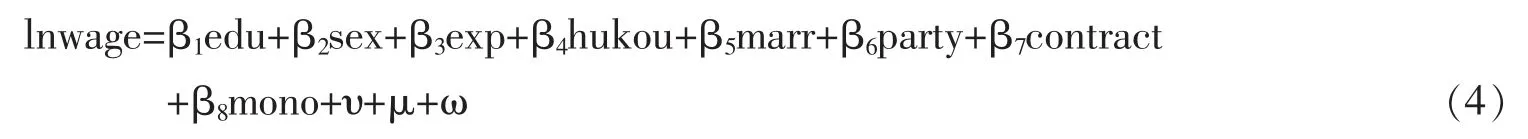
其中，从左到右依次表示对数工资，教育类别变量、性别、工作经验、是否农业户口、婚姻状况、是否党员、是否签订劳动合同、是否在垄断行业，向下的残差、向上的残差和一般残差。

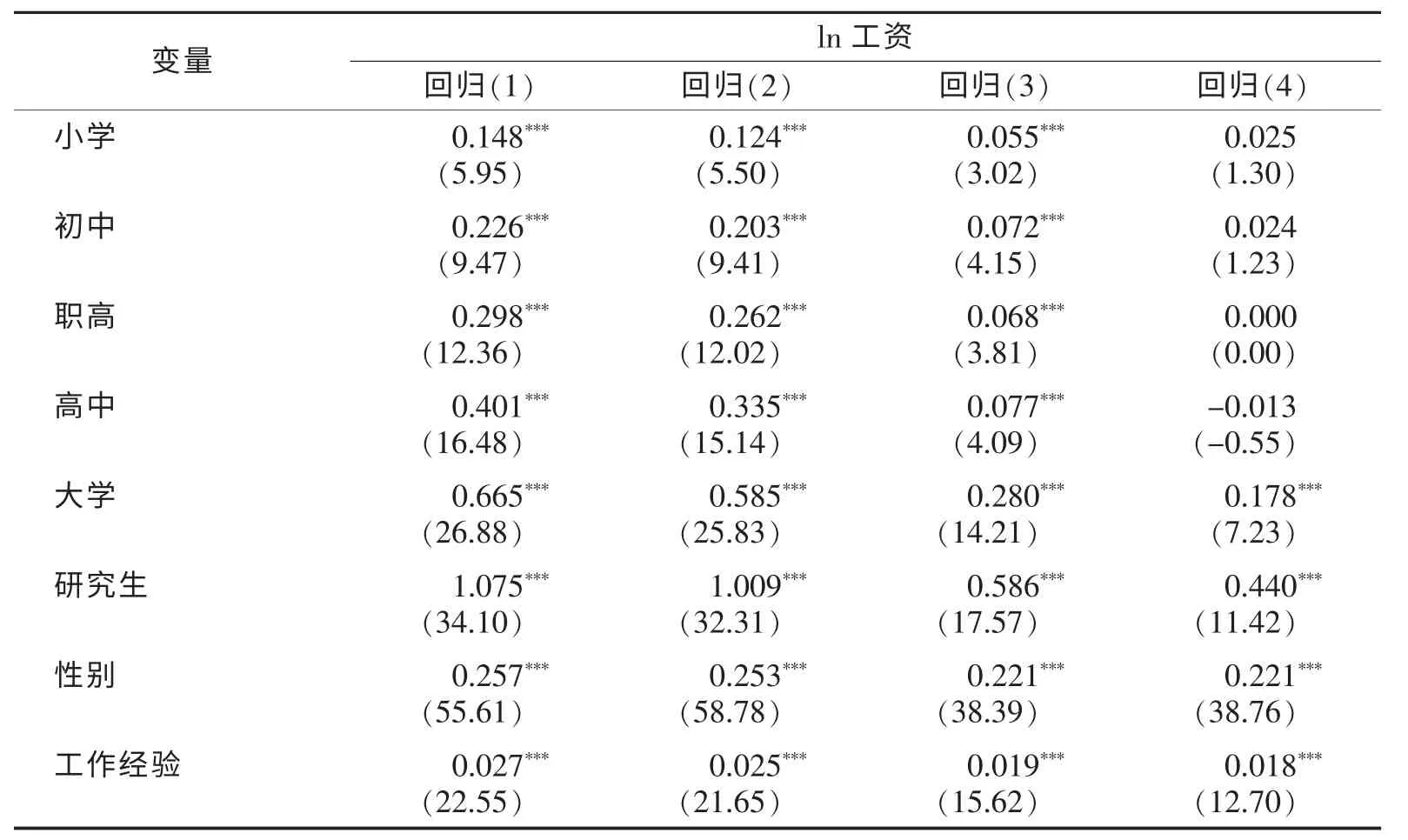
表2 模型筛选

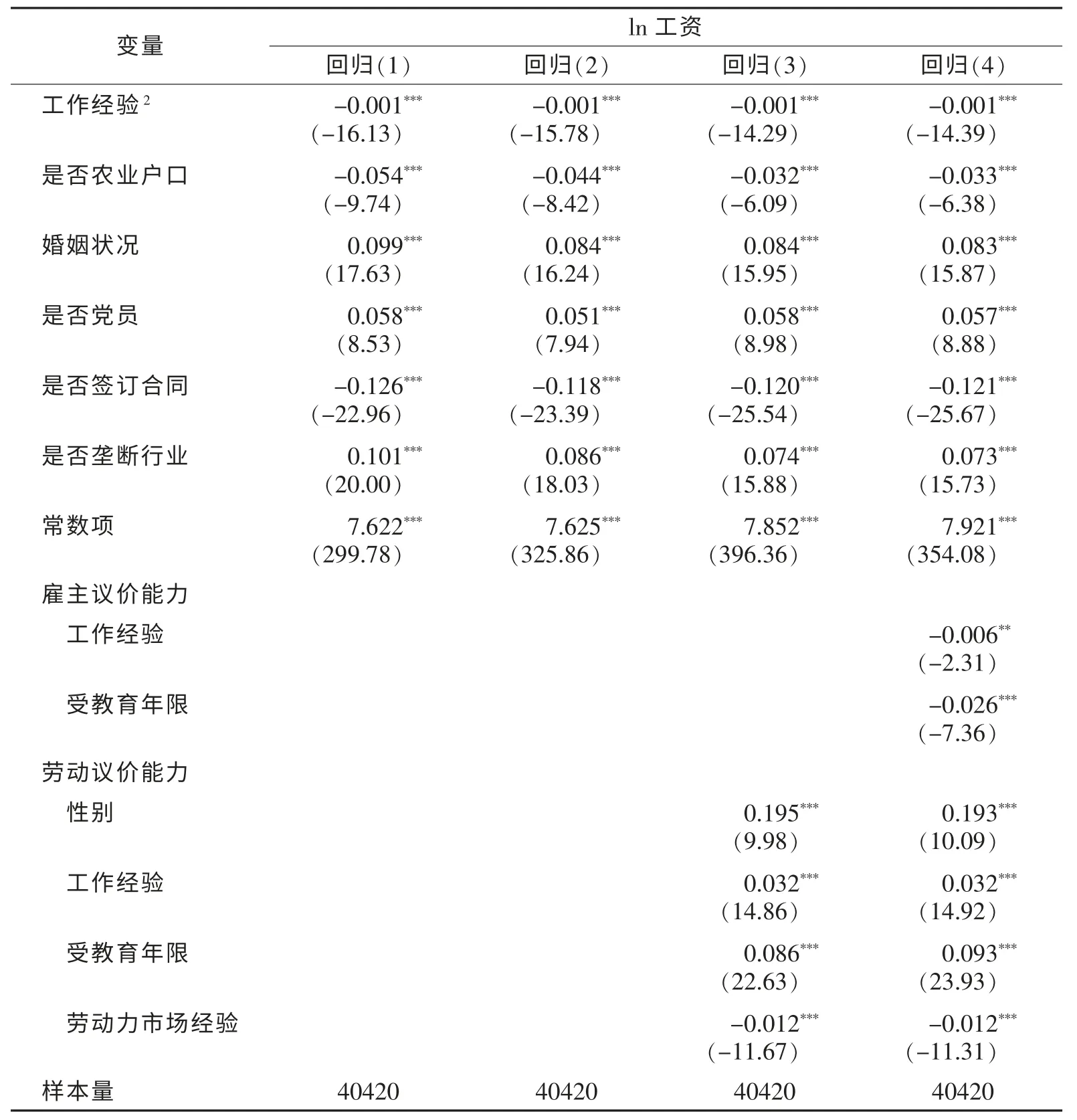
表2（续）

如表2所示，回归（1）是以工资的自然对数为因变量以个体特征为自变量的OLS估计。回归（2）至回归（4）是以工资的自然对数为因变量以个体特征为自变量的双边随机前沿MLE 估计，回归（3）、回归（4）是异质性双边随机边界估计，分别引入了员工议价能力的影响因素（性别、劳动力市场经验、受教育年限、工作经验）和雇主的议价能力影响因素。假定雇主“看人下菜”，对不同劳动力采用不同的议价策略，因此劳动力的一些属性（受教育年限、工作经验）也影响雇主的议价能力。我们也试图引入雇主所在地区是否为发达地区、雇主所在行业是否为垄断行业等地区、雇主层面的因素来影响雇主的议价能力，但模型结果显示均不显著。

通过似然比检验发现，异质性双边随机边界优于普通双边随机边界模型，加入雇主议价能力影响因素的双边随机边界模型优于只加入员工议价能力的模型。回归（4）中劳动力市场经验对员工的议价能力起负面作用，考虑到劳动力市场经验的计算方法（年龄—受教育年限），劳动力市场经验的符号可能反映了年龄的符号，即员工年龄越大，其议价能力越低。雇主的议价能力方面：对受教育年限高的员工，雇主的议价能力下降，可能是因为雇主想留住人力资本水平高的员工，从而无法大幅压低工资；工作经验（在本企业工作时间）的符号为正，说明雇主对在其单位工作时间长的员工会增加压低工资的力量，可能是因为工作时间长，积累的企业专用性人力资本较多，从而使员工不愿意跳槽（会损失专用性人力资本）。工作经验也会加强员工的议价能力，因为员工积累了专用性人力资本造成雇主不方便替换在职员工。

（四）议价能力的估计和比较

选用回归（4）进行每个城市的MLE 估计。对46个城市逐一进行回归（4）的MLE估计（以削弱补偿效应、集聚效应对议价能力计算的影响），计算每个城市内的每个劳动力的议价情况。如利用上海市的子样本计算出ID为45265的上海市劳动力个体的工资议价情况为[员工：0.160，雇主：0.135]，员工占优；利用西宁市的子样本计算出ID为155393的西宁市劳动力个体的工资议价情况为 [员工：0.126，雇主：0.259]，雇主占优。然后再将所有的子样本连同议价能力变量合并成一个总样本。

为了直观地辨认劳资议价结果与城市规模的关系，绘制以平均议价结果为纵坐标，市辖区职工数的自然对数值为横坐标的散点图[在缺乏市辖区常住人口数据的情况下，根据陈杰和周倩（2016）的研究，市辖区职工数可以作为城市规模的度量指标]。从图1、图2和图3可以看出，总体上资本议价能力随着城市规模增加而减弱，劳动力议价能力随着城市规模增加而增强，城市规模越大，议价结果越有利于劳动力。

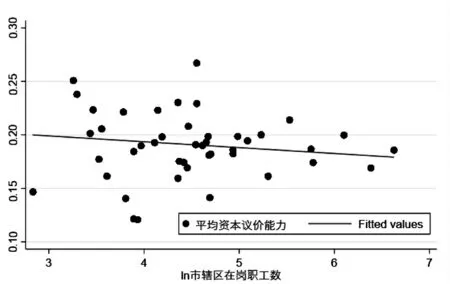
图1 城市规模与资配议价能力

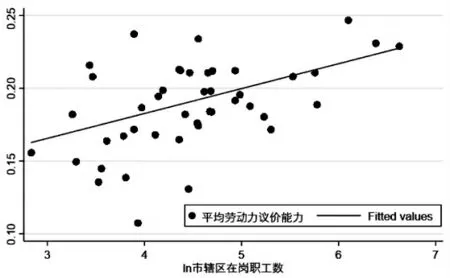
图2 城市规模与劳动力议价能力

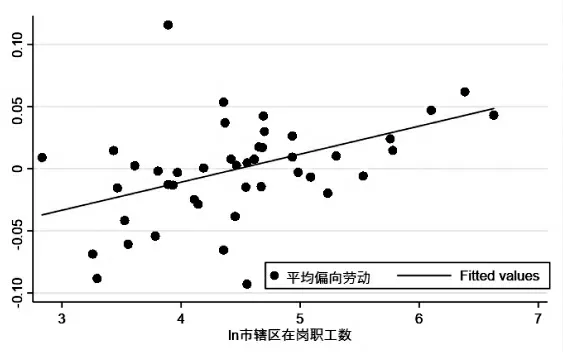
图3 城市规模与议价结果

为查看控制个体和城市异质性后议价能力如何随城市规模变化，分别以三个代表议价能力的指标（资本议价能力、劳动力议价能力、议价结果偏向劳动力的净效应）为因变量，以城市特征[城市规模、城市人力资本水平（以高等学校教师数衡量）、城市人均GDP、城市产业结构（以第二、第三产业就业人数比表示）、是否东部沿海]和个体特征（是否在垄断行业、受教育程度、性别、婚姻状况、工作经验、劳动力市场经验、是否党员、是否签订劳动合同）为自变量建立回归模型。回归结果见表3。结果表明，随着城市规模的增加，资本的议价能力下降，劳动力的议价能力上升，议价结果更加偏向劳动者。

借鉴孟美侠等（2019）研究城市规模工资溢价的思路，用匹配法研究城市规模对议价能力的非线性影响以及削弱城市间劳动力自选择（选择效应）对结果的干扰。将市辖区职工人数等分为四个部分（分割点为79万人、110万人、323万人），分别对应1类城市、2类城市、3类城市和4类城市。然后，根据所在城市的规模不同对劳动力个体进行匹配，如1类和2类城市的劳动力匹配，2类和3类城市的劳动力匹配，以便消除各个城市间劳动力构成的不同对议价能力和工资造成的影响（即消除选择效应的影响），同时观察城市规模对劳资议价能力的非线性影响。使用PSM 进行两组变量的匹配，发现不容易使所有变量在两组之间同时无差异，因此改用熵平衡法（Entropy Balancing Method）进行匹配。对规模1与规模2的劳动力进行匹配后，求得城市规模对劳动力议价的影响。

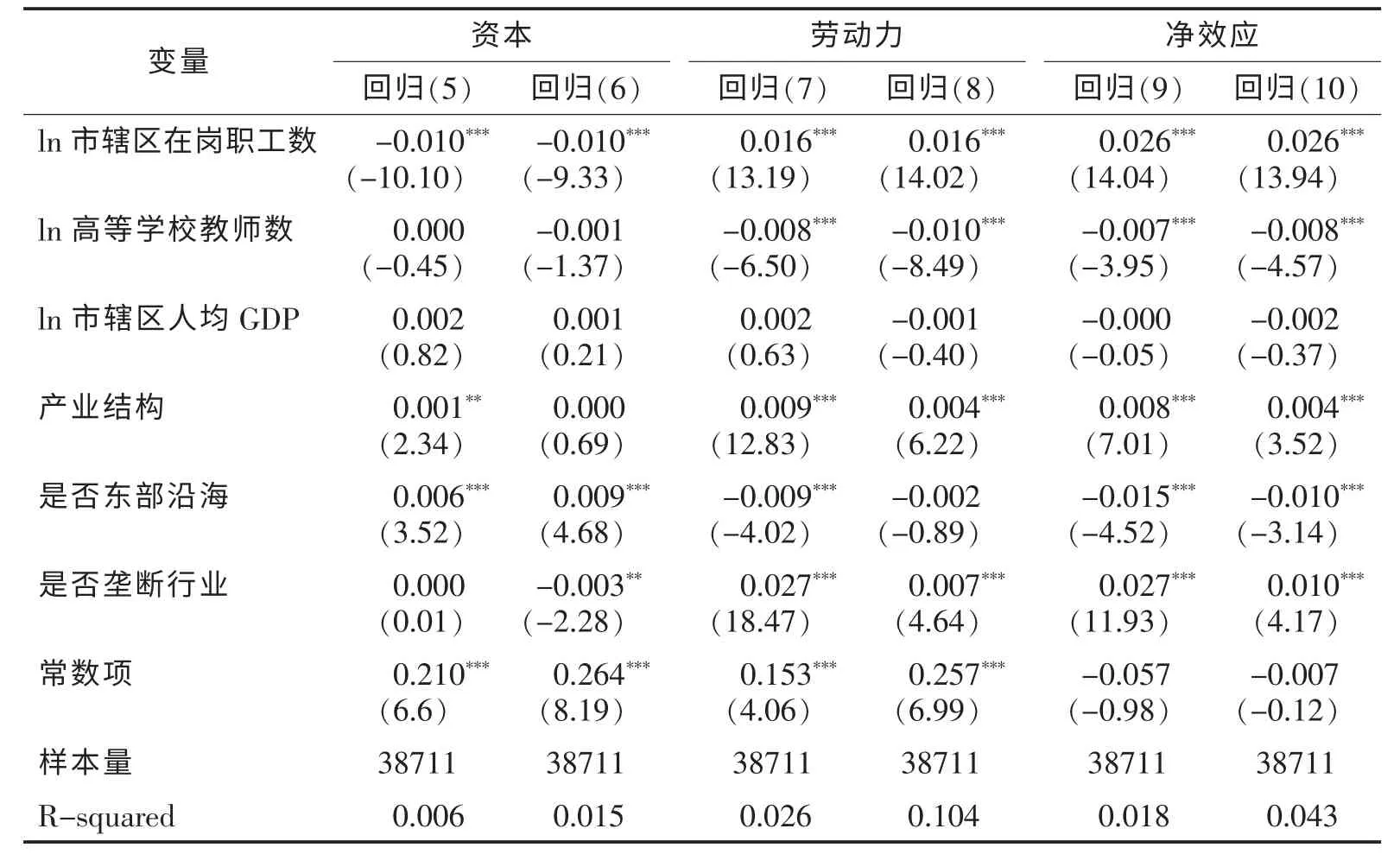
表3 回归分析

对1类城市与2类城市进行匹配，以1类城市为控制组，2类城市为处理组，求得城市规模扩大对议价能力的影响。从平衡性检验①平衡性检验过程和结果略，下同。可以看出，用熵平衡法后各个变量在均值、方差、偏度三个维度上都实现了平衡。以是否为2类城市的虚拟变量为自变量、以三个议价能力变量为因变量进行匹配后的加权回归得到1类和2类城市议价能力差异，如表4所示。

从表4可以看出，如果一个劳动力从1类城市迁移到2类城市，其自身的议价能力增加1.6%，则其所面对的雇主的议价能力减弱0.8%，雇主和员工综合作用的结果是议价能力偏向劳动力的程度增加2.5%，从1类城市到2类城市议价结果更偏向劳动力。

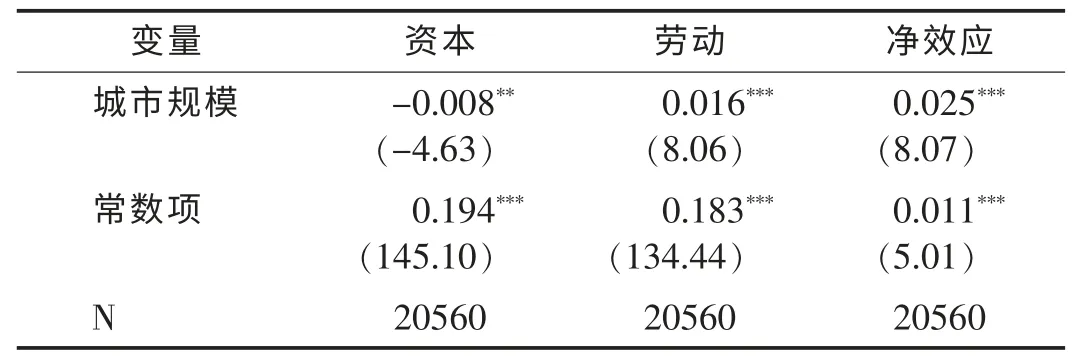
表4 议价能力差异（1类和2类城市）

将劳动力按学历（大专为界）划分为高技能和低技能劳动力进行异质性分析（回归结果省略），结果显示，从1类城市到2类城市，低技能劳动力的议价能力增加1.8%，低技能劳动力雇主的议价能力减小1.7%，议价结果更偏向劳动力，程度为3.5%。从1类城市到2类城市，高技能劳动力议价能力增加1%，但其雇主议价能力也增加2%，因此议价结果偏向资本的程度变化量为1%，这个偏向变动在5%统计意义上不显著。以上结果说明：从1类城市进入2类城市，低技能劳动力获得更有利的议价结果，而高技能劳动力没有获得更有利的议价结果。

表5 议价能力差异（2类和3类城市）

对2类城市与3类城市进行匹配（平衡性检验图表略），以2类城市为对照组、3类城市为处理组、以是否为3类城市的虚拟变量为自变量，以三个议价能力变量为因变量进行匹配后的加权回归结果，如表5所示。

从表5可以看出，如果一个劳动力从2类城市迁移到3类城市，其议价能力几乎不变，其雇主的议价能力也几乎不变，雇主和劳动力的议价能力综合作用的结果是从2类到3类城市，劳动力议价结果不改变。

将劳动力按学历（大专为界）划分为高技能和低技能劳动力进行异质性分析（回归结果省略），结果显示从2类城市到3类城市，高技能劳动力的议价能力增强0.25%（不显著），高技能劳动力雇主的议价能力减弱1.13%，议价结果更偏向劳动力，程度为1.4%（统计不显著）。从2类城市到3类城市，低技能劳动力议价能力几乎不变，其雇主的议价能力也几乎不变，因此议价结果几乎不改变。以上结果说明，如果劳动力从2类城市进入3类城市，高、低技能劳动力的议价能力几乎不变。

对3类城市与4类城市进行匹配（平衡性检验图表略），以3类城市为对照组，4类城市为处理组，以是否为4类城市的虚拟变量为自变量，以三个议价能力变量为因变量进行匹配后的加权回归结果，如表6所示。

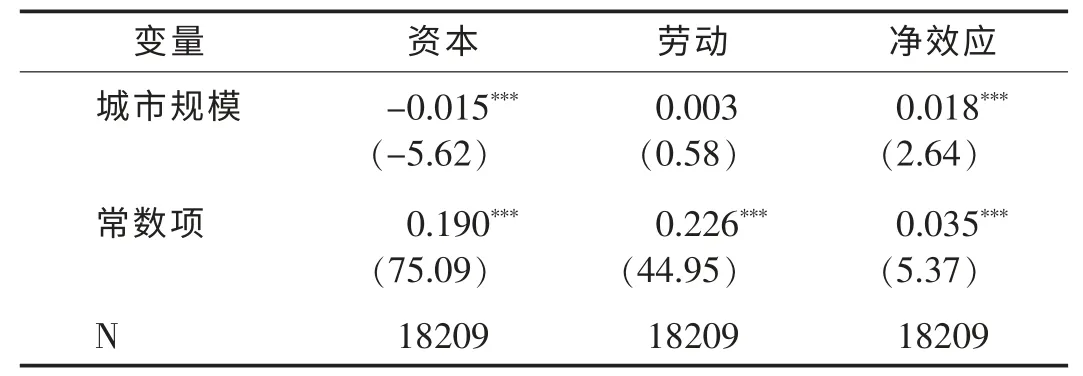
表6 议价能力差异（3类和4类城市）

从表6可以看出，如果一个劳动力从3类城市迁移到4类城市，其议价能力几乎不变，其雇主的议价能力减弱1.5%，雇主和劳动力的议价能力综合作用的结果是从3类城市到4类城市，劳动力的议价结果更偏向劳动力，程度为1.8%。

将劳动力按学历（大专为界）划分为高技能和低技能劳动力进行异质性分析（回归结果省略），结果显示从3类城市到4类城市，低技能劳动力的议价能力增强0.7%，低技能劳动力雇主的议价能力减弱3.3%，议价结果更偏向劳动力，程度为4.1%，这个偏向变动在1%统计意义上显著。从3类城市到4类城市，高技能劳动力议价能力几乎不变，其雇主的议价能力略微增强，因此议价结果略微偏向资本（统计不显著）。以上结果说明，如果劳动力从3类城市进入4类城市，低技能劳动力议价能力增强而高技能劳动力议价能力略微减弱。

（五）稳健性检验

如果一个城市的劳动力议价能力是某种外生因素决定的，比如制度环境，那么可能是有利于劳动力的制度环境吸引了更多人才进入该城市，从而使城市规模变大，即以城市常住人口衡量的城市规模受到劳动力议价能力的反向影响。为了削弱这种反向影响，我们采用《2017 城市统计年鉴》中的“市辖区年平均人口”作为市辖区年平均户籍人口。由于大城市户籍比较难获得，因此低技能劳动力涌入不会影响大城市户籍人口，而大城市户籍人口所代表的城市规模却会影响低技能劳动力的议价能力。所以运用以户籍人口划分的城市规模对低技能劳动力议价能力进行回归来削弱由于反向因果带来的相关性，结果更加稳健。因为没有针对户籍人口的城市规模划分标准，我们根据样本分布将样本均分为4类。将4类城市的样本按上文方法依次匹配后求得议价能力偏向的变动情况，发现在偏向变动方向上与上文相同，但具体的变动数值有所不同。这说明上文的研究结果基本上是稳健的。

四、结论与不足

本文从雇主垄断性与城市规模的关系角度推理出城市规模与劳动力工资议价能力的关系并运用流动人口数据和大城市样本进行了实证检验。研究发现：城市规模对劳动力工资议价能力的影响是显著的，城市规模增大使议价结果朝着有利于劳动力的方向变动。异质性分析发现，当低技能劳动力进入规模较大的城市时，其议价能力增强，而其雇主的议价能力减弱，综合作用的结果是低技能劳动力在大城市可以获得更多的经济剩余；对高技能劳动力来说，进入大城市可能使其议价能力增强，但大城市雇主的议价能力也增强了，因此综合作用的结果可能会使议价结果朝着对资本有利的方向变动。

本文存在以下不足：虽然使用了数据量很大的流动人口调查数据，但层层筛选留下的数据量不够多，又分别对每个市辖区进行MLE 估计，有些市辖区只有200 多个劳动力个体，因此不足以精确计算一些小样本城市的工资决定方程和议价能力指数；采用截面数据未能控制劳动力不可观测的能力差异对议价能力的影响，但如果控制了该影响，本文的结果可能会变得更微弱。