基于决策树算法的广州南至珠海旅客发送量预测
林少毅
(中国铁路集团广州局铁路集团公司 广东省广州市 510000)
目前,对铁路客流预测的研究“汗牛充栋”,不同学者采用不同的模型方法进行预测。不同模型算法都有明显的优点也必然存在明显的局限性,比如:
(1)以神经网络模型为代表的深度学习算法[1],该算法较为复杂,在梯度下降更新权重时有概率落入局部极值,同时,随着神经网络层数的增加,梯度下降优化损失函数导致计算量和计算时间呈指数级增加,经济性较差。
(2)多元回归算法[2]与时间序列模型及算法[3-5],多元回归算法和时间序列算法属于正统的统计学模型,以线性假设为基础,对输入的样本数量和样本质量要求较高,遇到非线性结构数据时往往“水土不服”,预测结果自然也较差。
(3)灰色理论模型[6]、集成学习算法模型,支持向量机算法等[7],其中,集成学习算法建立在单个决策树算法的基础上,在数据结构和数据量并不复杂时,容易产生过拟合现象,需要根据经验设置合理的学习率等参数,添加正则项,而且迭代过程占用很大的计算资源。
综合以上考虑,本文选择决策树理论中的CART 算法对广州南至珠海区间的二等座旅客发送量进行预测。
1 决策树理论及算法选择
1.1 决策树算法选择
决策树算法是一种监督学习,就是事先给定样本,按照一系列规则对样本数据的特征值进行判断,并不断迭代循环最终完成分类或回归的过程,最后形成一个类似于“倒立的树”的模型(算法)。由于样本包含许多特征,总有一些特征在分类时起到“关键”作用,就需要通过规则找到这些具有决定性作用的特征,决定性作用最大的那个特征先找到并作为根节点,然后迭代循环找到各分支下次大的决定性特征,直至各个分支下所有数据都属于同一类[8]。本文选择CART 算法来构建决策树。
1.2 CART算法
CART 算法生成决策树可以分为分类树和回归树两种类型,生成方式有一定的区别。当输出结果为离散值时,代表CART 决策树;当输出结果为连续值时,便是CART 回归树,此时不再采用基尼系数而是采用下面公式(1)来选择特征值和特征值划分点。其算法过程如下:设xi为第i 个样本的输入值,yi为对应的输出值。对于每一个特征变量j 选择最优切分点s,选择切分的依据是:

在选择特征变量j 和该特征变量对应的切分点s 的情况下,选择使式(1)取得最小值的对(j,s),其中,R1和R2是选择特征变量j 和该特征变量对应的切分点s 的情况下将输出集合分为了两部分,R1和R2的计算方法如式(2)所示:

图1:旅客发送量情况
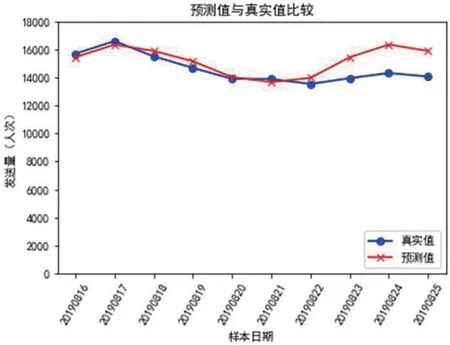
图2:预测值与真实值比较

c1和c2为输出集合的均值,计算方法如式(3)所示:

不断的重复上述过程,直到达到终止条件,便得到了CART 回归树。
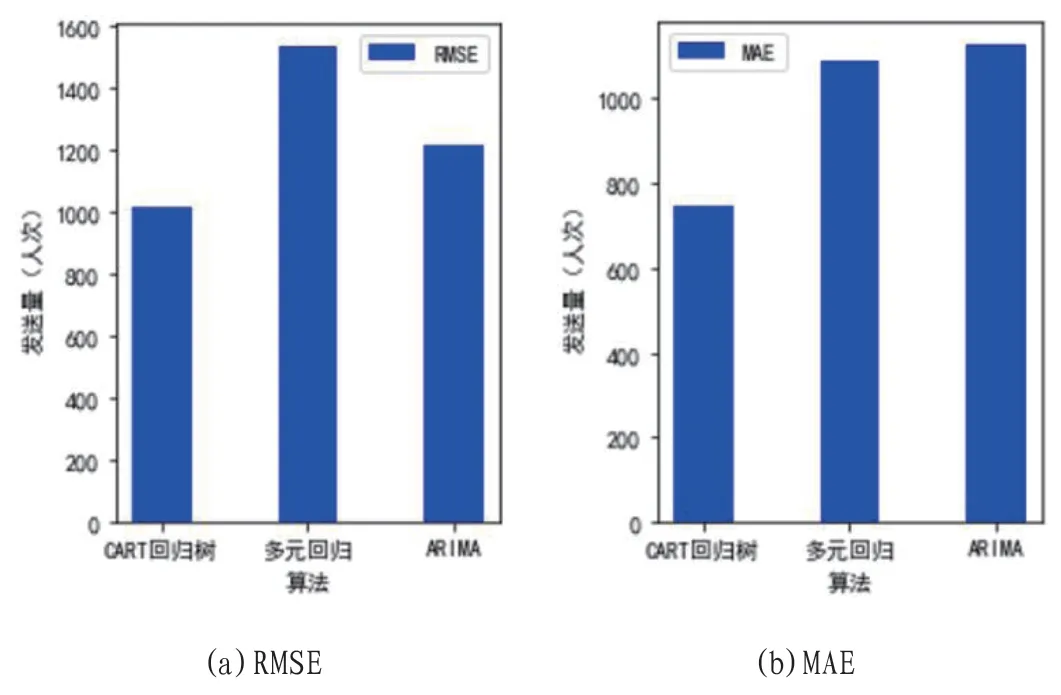
图3:三种算法预测精度的比较(RMSE)
2 算例应用
2.1 样本与特征选择
影响旅客出行需求的因素较多,比如:台风、暴雨、降雪,或者疫情、事故等人为封锁导致交通无法正常运营等短期因素。从长期来看,影响广州南至珠海间铁路客流的主导因素是两地间经济人文交流以及其他运输方式的竞争性替代。而短期内,其他交通方式供给比较稳定,不会有大的波动;两地间的经济人文交流也呈现出一种总体稳定趋势上升的情况。因而,广州南至珠海的铁路日旅客发送量呈现出一种长期的趋势性增长和短期的以月份,周号为代表的周期波动特点。综上所述,选择月份,周号,当月当周号平均发送量、去年同期当月当周号的平均发送量为样本输入特征值。
样本数据方面,选取2019年6月1日至2019年8月25日为本期的样本日期段,由于小长假客流特点与平时的客流特点截然不同,为了防止小长假客流对最终的算法输出结果产生干扰,去除2019年端午节包含的3 天假期。由于端午节节前一天和节后一天的客流特点也受到小长假放假的影响,因而一并去掉,最终选择样本数据一共包含81 天。每个样本包含月份,周号,当月当周号平均发送量、去年同期当月当周号的平均发送量这4 个特征指标。日旅客发送量整体情况如图1所示,可知,日旅客发送量最大为17358人次,最小为8331 人次。平均日旅客发送量为12426 人次。另一方面,从图1(a)明显看出日旅客发送量有很明显的趋势性和周期性(大致以一个星期为周期单位)。图1(b)分周号旅客日发送量平均值,可以看到周六旅客平均日发送量最高为13660 人次,其次为周五,旅客平均日发送量为13366 人次,最低为周二,旅客平均日发送量为11322 人次。
2.2 算法实践
本文使用Python 来进行CART 回归树的算法建立。将81 组样本分为训练集和测试(预测)集两部分,训练集包括前71 组样本数据,后10 组样本数据进行模型测试检验和预测。最终得到CART 回归树算法。将测试集样本数据输入算法进行检验,最终预测值与原样本数据进行比较,结果如图2所示,我们选择公式(4)来对每个样本的误差相对值进行计算和评价。可以看到,10 个测试样本中相对误差最大14.16%,相对误差最小为0.87%,相对误差平均值为5.22%。训练出的CART 回归树算法拟合效果基本达到预期,如图2所示。

2.3 结果分析与比较
为了更准确客观的对预测结果进行分析和比较,采用均方根误差(RMSE)和平均绝对误差(MAE)两个指标来对预测结果进行评价。计算公式如下:

其中,yi为样本真实值,为算法预测值,n 为测试集的样本个数(本算例中n=10)。同时采用多元回归算法和时间序列算法中的ARIMA 模型进行比较验证。使用的训练样本和测试样本与输入CART 回归树算法保持一致,最后使用式(5)和式(6)对预测结果进行评价,最终三种算法的预测效果和精度如图3(a)和图3(b)所示。可知CART 回归树算法在均方根误差(RMSE)和平均绝对误差(MAE)的评价下预测精度都是最高的,明显优于多元回归算法和时间序列算法中的ARIMA 模型。
3 结论
本文采用决策树理论中的CART 回归树算法对广州南至珠海区间的旅客发送量进行预测,结果表明采用的CART 回归树算法能够较好的完成预测任务,预测精度明显优于多元回归算法和时间序列中的ARIMA 模型。但本文使用的CART 回归树算法能够将误差范围限定在一个较小合理的范围内,则输出的预测结果就完全可以为铁路运输企业制定决策提供依据。下一步,将逐步引入天气、经济活动等其他影响因素进入CART 回归树算法,通过不断优化迭代,进一步提高算法的预测精度。

