优化K-means的不平衡数据分类研究

王舒梵

（上海工程技术大学数理与统计学院 上海市 201600）

1 绪论

K-means 算法最早由Steinhaus 等人[1]提出，是一种经典的基于数据分类的聚类算法。该算法简单易懂、收敛速度快、执行效率高，因此被研究学者们广泛使用。但是传统的K-means 算法不易受聚类数K 的影响，且对初始聚类中心的选择依赖性较大，所以，本文将优化K-means 算法实现不平衡数据分类的研究。

优化K-means 的不平衡数据分类算法，考虑到不平衡数据中数据不精确、过拟合、误差与方差大等问题，结合K-means 算法中不平衡数据不易受聚类数K 的影响，且对初始聚类中心的选择依赖性较大等问题，本文提出了一种优化K-means 算法的不平衡数据集分类算法，采用基于最大距离选择法实现聚类中心的查找，将不平衡数据集划分为测试集与训练集，多次调用优化的K-means 算法，得到不平衡数据的模型，进而得到不平衡数据集合的分类结果；通过性能分析，确定该算法的聚类准确性更高且分类结果更加的精确与稳定。

2 关键技术概述

2.1 不平衡数据分类

不平衡数据分类的研究，集中于多数类领域，常见算法主要用以提高不平衡数据集的性能，典型有代价敏感学习算法、单类学习算法以及集成学习算法。

代价敏感学习算法是指通过构建错分代价最高的类，以总代价最小为实现目标，实现不平衡数据分类的研究。典型算法有AdaCost[2]算法，该算法在AdaBoost 算法的基础上通过代价敏感学习模型，修改权重值，完成策略的更新，调节不平衡数据分类，减少代价之；而MetaCost[3]是在传统的分类模型上转化代价敏感模型，采用传统分类模型训练数据集合，对每个样本计算，以确定不同的类别内容，以最小代价类作为其标签，由修改后的训练集合再次学习分类模型；Cao 等[4]采用Stacking 集成方法，提出一种基于特征逆映射的成本敏感型堆叠学习（IMCStacking），来分类不平衡数据，解决分类研究中的问题。但是，代价敏感学习算法在数据搜索的过程中，消耗大量的时间空间值，并且仅仅以数据集中样本量大小或者样本间的比例为误分类代价，无法得到精确地分类效果。

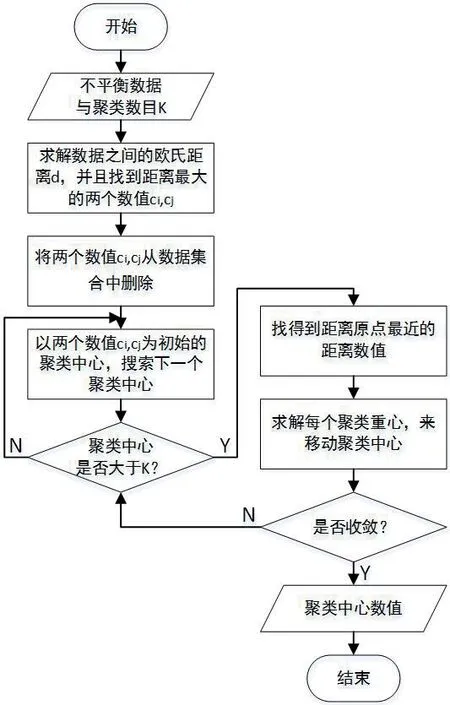
图1：算法流程图

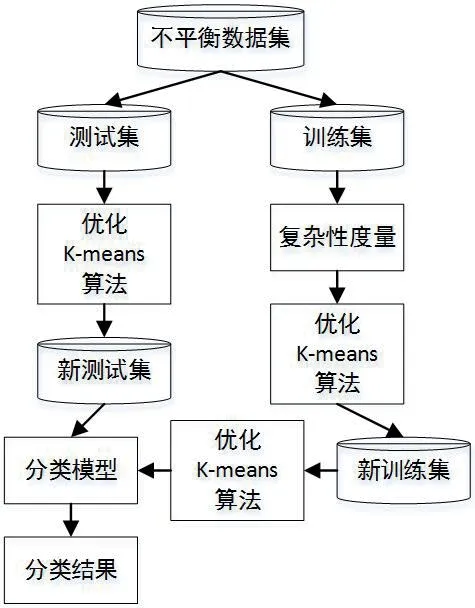
图2：不平衡数据分类研究的框架

单类学习算法通过分类与训练单个类别的样本集合，完成不平衡数据的分类研究，在不平衡数据集合中，通过只训练多数类样本能够得到一个模型，进而从测试样本中识别出多数类，典型的单类学习算法有单类支持向量机（One-Class SVM）、支持向量数据描述（Support Vector Data Description，SVDD）以及其他的改进算法等[5-7]。Sarah 等[8]针对于高维度空间数据分类低效率的问题，提出了一种混合模型，即训练无监督的DBN，以提取不平衡数据的通用特征值，通过这些数值训练与分类单类支持向量机，该模型具有可伸缩性和较高的计算效率。但是，因为单类学习算法通常只能对单一类别的样本值进行训练而只能在一定程度上减少时间开销，进而只适用于少数类样本，容易导致过拟合等问题。

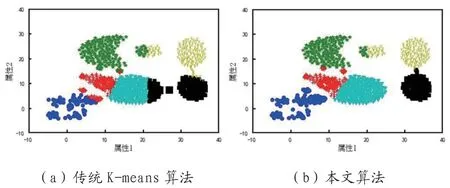
图3：性能对比

集成学习算法通过组合多个个体学习器来完成学习模型的构建，能够获取比单一学习器更加优越的模型效果。典型算法有Bagging、Boosting、Stacking 等[9-11]是集成学习中典型的三类方法，其中，Bagging 中训练子集相互独立，能够有效降低个体分类器的方差，减少了泛化误差，且分类器并行的生成能够提高运行效率;但是，该算法只适合小数据集。Boosting 算法是一种将弱学习器转换成强学习器的迭代方法，但是，该算法在提高个体学习器效果的同时会产生过拟合问题，且各个体学习器顺序生成会导致训练效率相对较差。Stacking 算法通过对多个个体学习器的训练与分类，将输出值作为输入完成学习模型的训练，得到最终的输出，该算法减少了模型的泛化误差，但容易过拟合。

考虑到上述问题，本文将采用K-means 算法来实现不平衡数据集分类的研究。

2.2 K-means技术

将K-means 算法应用于不平衡数据集分类中，能够避免传统不平衡数据分类中存在的数据不精确、过拟合、误差与方差大等问题。不平衡数据分类算法需要对训练集学习后，通过对未知数据的分类而得到数据集合的预测值，K-means[12]聚类算法是一种无监督学习框架，旨在将数据中属性相似的示例集中在一起，而不需要对训练集进行精确地学习。该算法是将给定的数据集划分为K 个类别主要步骤如下：

（1）从数据集X 随机选取K 个对象，作为K 个类别的初始聚类中心

（2）分别计算数据集合中每个元素同聚类中心的欧式距离，依据最近邻原则，将不同的元素划分到相应类别；

（3）求解每个类别中元素的均值，并且作为新的聚类中心，重复上述步骤；

（4）指导聚类中心不再变化，停止循环。

其中，欧式距离是指两个样本值在欧式空间中的直线距离，xi与xj 在m 维空间中，欧式距离的计算公式如下：

3 基于优化K-means的不平衡数据分类算法

3.1 优化的K-means算法

针对于传统K-means 算法中不平衡数据不易受聚类数K 的影响，且对初始聚类中心的选择依赖性较大等问题，本文提出基于最大距离选择法实现聚类中心的查找。首先，输入不平衡数据与聚类数目K，求解欧式距离，不断寻找最值，采用趋近法寻找聚类中心，结合数据的收敛程度，最终确定不平衡数据集合中的聚类中心。找到多个不同的聚类中心后，即确定了不平衡数据集合不同类别的中心数据，将趋近与不同聚类中心的数据自动话费为一个区间，完成不平衡数据的分类处理。

核心算法流程，如图1所示。

3.2 基于优化K-means算法的不平衡数据分类

表1：实验配置

表2：运行时间对比（单位：ms）

不平衡数据集合能够划分为训练集合与测试集量部分，其中，训练集同意训练分类模型，测试集用以测试模型的性能。因为训练集为不平衡数据集合，因此需要优化的K-means 算法来降低不平衡性，之后，通过测试集完成对数据集的测试与分类处理，得到不平衡数据的分类处理结果。整体框架，如图2所示。

通过多次使用优化的K-means 算法实现多个训练集与多个测试集，最终得到分类模型，进而得到不平衡数据集合的分类结果。

4 性能分析

为了验证本文算法的性能，采用随机生成的人工数据集，代替不平衡数据集进行实验与测试。实验配置如表1所示。

随机选取1000 条数据代替不平衡数据集合，每条数据属性假设有两个，通过对比传统K-means 的不平衡数据分类算法与本文算法，来验证本文算法的聚类准确性更高且分类结果更加的精确与稳定。对比结果，如图3所示。

由图可知，图（a）中传统K-means 算法的聚类结果较为集中，并且出现了离群点的问题；而本文算法则没有离群点作为聚类中心的问题，进而保证了聚类的准确性，为分类结果的精确性与稳定性奠定了理论基础。

针对于结果的精确度与稳定性，本文采用优化的K-means 算法来反复迭代训练集与测试集，进而得到更加精确与稳定的测试结果。而针对于时间复杂度，时间换取精确度的方法来完善。通过文献资料的查阅得知，传统K-means 下不平衡数据分类的时间复杂度为其中，n 为聚类样本个数，k 为类别数量，T 为聚类中心的迭代次数。而本文算法的时间复杂度，计算结果为其中t 为本文算法的迭代次数。当即时，本文算法消耗的时间小于传统K-means 算法用于不平衡数据分类的时间，而由于n 为聚类样本个数可知，恒成立。以A、B、C 表示分类结果为例，算法的运行时间，如表2所示。由表可知，本文算法的运行时间短于传统的K-means 算法。因此，本文算法在具有更精确与稳定的分类结果的同时，消耗更短的时间。

综上所述，在不平衡数据分类研究领域，本文算法优于传统的K-means 算法。

5 总结

本文在不平衡数据分类的基础上，采用优化的K-means 算法，来解决数据分类不精确、过拟合等问题，最后通过性能分析，确定了算法的良好可用性。