基于遗传算法整定PID的倾转翼飞机过渡段定高控制

郑光廷 王琦 陈龙胜 杨龙飞 王蓉

摘 要：针对倾转翼飞机过渡段模式飞行时，其动力学特性呈现出的强非线性和强耦合的特点，传统的PID控制方法难以设计其控制参数并实现定高控制。本文将遗传算法和PID控制理论相结合，基于遗传算法整定获得全局最优的PID控制参数以保证良好的定高控制效果。仿真试验结果表明，经遗传算法整定参数后的PID控制能够更好地实现对倾转翼飞机过渡段的定高飞行控制。

关键词：倾转翼飞机;过渡段;非线性;遗传算法;PID;飞行控制

中图分类号：TJ765

文献标识码：A

文章编号：1673-5048（2020）06-0085-06

0 引  言

倾转旋翼飞机兼顾直升机和固定翼飞机的飞行特点，既能够垂直起降、空中悬停，又可以高速平飞，具有广阔的发展前景和研究价值。国外一些国家在倾转旋翼飞机的研制方面已经取得了一定的成功，比如美国成功研制了民用BA609[1]和军用V-22倾转旋翼机，且V-22已经在美国空军服役。国内研究虽然起步较晚，但也取得了一定的成就，并研制出了“蓝鲸”和彩虹-10等倾转旋翼无人机。

然而，倾转旋翼在飞行过程中复杂的气动耦合以及系统表现出的时变、非线性特点，都大大增加了飞行控制难度，针对此类控制问题，国内外诸多学者进行了大量的研究，并取得了一定的成果[2-8]。Mehra等针对XV-15倾转旋翼机全模式的控制问题，提出了一种模型预测控制方法，仿真结果表明在许多模式下都表现出不错的效果[6]。Rysdyk等在非线性模型逆控制方法基础上引入自适应神经网络算法形成自适应模型逆控制方法，避免了原始方法控制器参数调整的复杂性和偶然性，同时也弥补了线性模型逆控制方法带来的模型误差[7]。夏青元等人针对倾转旋翼飞机姿态控制，采用余弦加权分配的方法解决了控制操纵冗余问题，并采用无模型自适应控制方法实现了对姿态的自适应控制[8]。范和平等人基于定量反馈理论设计了角速率回路的控制器和滤波器，采用PID控制理论设计了外环控制回路[5]。

与倾转旋翼飞机相比，本文研究的倾转翼飞机大大提高了垂直起降时的升力效率，降低了结构重量[1]，但与倾转旋翼飞机类似，在过渡段模式飞行时存在控制参数时变、非线性、强耦合的问题，给过渡段的飞行控制带来很大困难。

传统的PID控制方法因结构简单、鲁棒性好、可靠性高等优点，被广泛应用于工业过程控制中，但控制器的参数调整通常采用试凑法等类似于手动调参的方法，具有一定的偶然性，对于时变、强耦合、非线性的复杂系统，很难找到最优参数，从而影响控制效果。本文在传统PID控制算法基础上，引入遗传学算法对PID参数进行调整，依靠遗传算法的全局寻优能力，找到PID最优参数，以实现倾转翼飞机过渡段的定高飞行控制。

1 倾转翼飞机纵向非线性模型

1.1 模型假设

因为倾转翼飞机一般以马赫数小于3的速度在大气层内飞行，故在建模时可忽略一些非主要因素的影响，以降

低建模的难度，使模型准确性与简洁性并具。假设如下：

（1） 将倾转翼飞机整体视作刚体;

（2） 倾转翼飞机过渡模式中无侧滑、翻滚、偏航，倾转翼飞机惯性积Ix，Iz为零;

（3） 不考虑倾转翼飞机运动过程中重力加速度的变化，即g取恒值为9.8 m/s2;

（4） 不考虑倾转翼倾转过渡过程中对飞机质量和质心的影响;

（5） 不考虑两旋翼之间的气动干扰;

（6） 不考虑机身、垂尾气动力对模型的影响;

（7） 由于倾转翼飞机外形对称，重心在纵轴上，无尾桨，两侧旋翼的反向扭矩相互抵消，因此可以假定横向通道与纵向通道解耦[9-10]。

为简化起见，本文在建立倾转翼飞机气动力模型时，假设飞机各部分气动力互不干扰，采用分体法分别建立倾转翼、固定翼、旋翼和平尾的气动力模型。由于飞机是关于Oxz平面左右对称的，故首先对飞机的一侧进行气动力分析，然后通过坐标转换到机体坐标系下并进行叠加，得到整个飞机的气动力模型。为便于分析，定义如下坐标系：

机体坐标系Sb-Oxyz：坐标系固连于倾转翼飞机，坐标系原点O位于飞机质心，x轴位于飞机的对称面内，沿机身轴线指向机头方向为正，y轴与飞机对称面垂直，飞机前飞时指向飞机右侧为正，z轴位于飞机对称面内，垂直于x轴，指向飞机下方为正。

地面坐标系Sg-Ogxgygzg：Og为地面上任取一点，xg轴位于水平面内并指向飞机前飞方向，zg轴垂直地面指向地心，yg轴位于水平面并垂直于xg軸，方向按右手法则确定。

气流坐标系Sa-Oxayaza：坐标系固连于飞机，其原点O位于飞机质心，xa轴与空速V重合，za轴在飞行器对称面内与xa轴垂直且指向飞机正下方，ya轴垂直于Oxaza平面，指向飞机前进方向右侧。

由于倾转翼飞机过渡段模式飞行阶段，飞机的气动中心基本无变化，故将倾转翼气动中心，旋翼拉力中心和倾转翼转轴中心统一用Ob1表示。图1为倾转翼飞机过渡段角度的定义。图中，Ob为飞机重心;Ob2为飞机升降舵气动中心;η为倾转翼与机体坐标系x轴之间的夹角，定义其向上偏转为正;αf0为倾转翼的安装角;αw0为固定翼的安装角;α为飞机迎角;μ为航迹角;dz定义为Ob1到Ob的距离，大小为0.15 m;dp定义为Ob2到Ob的距离，大小为0.5 m。

1.2 倾转翼飞机的气动力模型

1.2.1 固定翼的气动力模型

倾转翼飞机固定翼受力分析如图2所示。图中，Lw为升力;Dw为阻力;αw0为固定翼相对于机身的安装角;d=dz;αw为固定翼实际空速相对固定翼的迎角。

1.2.2 倾转翼的气动力模型

倾转翼相对于旋翼的安装角为αf0，亦为倾转翼的零升迎角，故忽略旋翼产生的来流对倾转翼的影响，同时，倾转翼的转轴中心与固定翼的气动中心同为Ob1，故倾转翼的气动力分析与固定翼类似。

1.2.3 旋翼的气动力模型

由于倾转翼飞机的旋翼采用的是转速可变的非变矩桨，且两边的旋翼以转速相同、方向相反的方式工作，故可用一个可变化的拉力T代替，T的作用点同样为Ob1，不考虑舵机环节，机体坐标系下旋翼的气动力为

1.2.4 平尾的气动力模型

为了使建模易于实现，把升降舵的舵力当作一个控制量，因为平尾与重心处于同一个平面内，且其气动中心与飞机重心在Oxy平面x轴的投影距离等于dp，故主要由平尾的升力为平尾提供俯仰力矩，定义当升降舵向上偏转时，产生向下的舵力为正方向，此时会迫使飞机抬头。经过分析可以得出：

平尾的气动中心速率为

平尾上的实际速度为

动压为

Vp相对平尾产生的迎角为

平尾水平安定面的升阻力为

平尾主要由安定面和升降舵组成，故整个平尾的气动力由安定面气动力和升降舵舵力合成。由于升降舵向上偏转时，会产生向下的正舵力σe，故平尾的升阻力为

由于Vp与机体坐标系的夹角为αVp，故其气动力转换到机体坐标系下为

1.2.5 倾转翼飞机的合力与合力矩

由于本文只对倾转翼飞机过渡段纵向运动进行分析，故只考虑机体坐标系x，z轴方向的合外力，且不考虑各部分间的气动力干扰，再将各部分的气动力及力矩叠加，因此就得到了整个倾转翼飞机的气动力和力矩，其表达式为

式中：FX，FZ为机体坐标系x，z轴方向的合外力（不包括重力）;M为气动力与旋翼拉力产生的俯仰合力矩。

考虑到倾转翼飞机非线性模型的复杂性，为降低建模难度，在过渡段建模过程中，由于倾转翼飞机关于纵向面对称，故不考虑横向运动对纵向运动的影响，且在水平无侧滑情况下进行分析，所以倾转翼飞机过渡段纵向运动方程可以表示为

式中：h为倾转翼飞机离地高度;Iy为飞机质量对y轴的惯性积;u，w，q分别为前飞速度、垂向速度和俯仰角速度;x，θ分别为水平位移和俯仰角。

由于倾转翼飞机的拉力、舵力都有一定限制，根据前期研究，得到可行的过渡段及平飞段前飞速度与时间的关系[9-11]，如图3所示，借此来降低系统的耦合程度，有利于对高度的控制。当飞机达到一定高度后，先通过翼面偏转使其低速前进，然后进入过渡段控制，直至进入平飞。

2 基于PID控制方法的倾转翼飞机过渡段定高控制

PID控制是控制领域最早应用的控制方法之一，是按照系统偏差的比例（P）、积分（I）、微分（D）方式对系统进行控制的方法，具有结构简单、鲁棒性好、可靠性高等优点，在工程领域得到广泛应用，其控制律为

式中：KP为比例系数;TI为积分时间常数;TD为微分时间常数。PID控制方法效果的好坏，很大程度取决于这三个参数的组合，所以选取何种方法进行参数调整变得尤为重要。本文将分别采用试凑法和遗传算法对控制器的参数进行整定。

采用试凑法手动调节PID控制器参数的过程如下：

首先调整比例系数KP。调整依据为，KP的值越大，比例作用越强，产生的矫正信号越强，系统调节的时间就越短。但过大的KP将会产生过大的矫正力矩，导致系统超调变大，影响系统的稳定性。调整KP时，可先忽略积分和微分作用，将KP的值由大到小进行调整，并同时观察系统的状态，找到合适的KP。

调整积分系数KI，调整的依据为，积分系数KI越大，随着时间的增加，产生的矫正信号越强，系统稳态误差就越小，进而系统的稳态性能就越好。但是过大的积分系数会增加系统的超调，降低系统的稳定性。在比例环节的基础上，加入积分环节会在一定程度上降低系统的稳定性，可以将比例系数KP适当调小来去除积分环节带来的影响，然后再由小到大调整KI，使系统稳态误差逐渐变小，从而得到更佳的稳态性能。

調整微分系数KD，调整依据为，KD越大微分作用越强，系统的动态性能就越好。但过强的微分作用会降低系统抵抗高频噪声干扰的能力。所以，对于追求高动态性能且对抗噪声干扰要求不高的系统来讲，可以选取较大的KD。

遗传算法（Genetic Algorithms，GA）是一种模拟自然界遗传机制和生物进化论的并行随机搜索智能优化算法[12]。1975年，密歇根大学的Holland在“自然和人工系统中的适应”书中首次提出了遗传算法，此后遗传算法被广泛应用于科学和工程优化问题的高质量求解中[13]。此次运用遗传算法整定PID参数，选择时间与绝对误差的积分作为目标函数即ITAE，目标函数值越小，系统瞬态响应的振荡越小，且能够很好地选择全局最优的控制器参数。其表达式为[14]

ITAE=∫∞0te（t）dt（24）

采用遗传算法整定PID的控制参数，结合建立的倾转翼飞机过渡段非线性模型，建立控制系统框图如图4所示。图中，y*为系统的期望输入即期望高度h*，y为系统的实际输出即实际高度h，U为系统的控制输入。

整个系统主要包括两个闭合回路，即高度控制回路和俯仰角控制回路。纵向姿态角控制回路采用双闭环控制策略，内环为角速度控制，外环为俯仰角控制;俯仰角的控制是高度控制的基础，所以把角度控制作为高度控制的内环，以实现定高转换的目标。

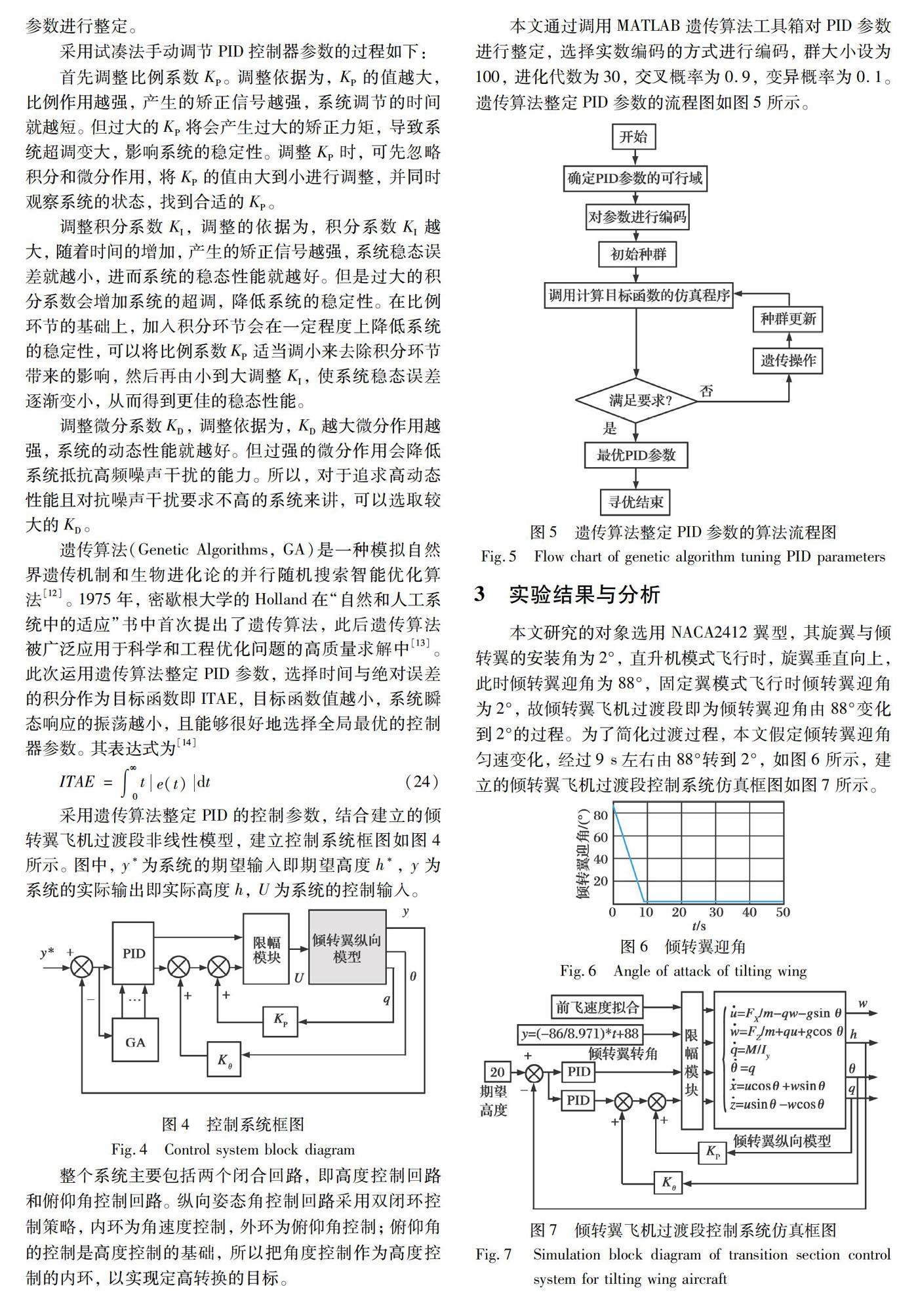
本文通过调用MATLAB遗传算法工具箱对PID参数进行整定，选择实数编码的方式进行编码，群大小设为100，进化代数为30，交叉概率为0.9，变异概率为0.1。遗传算法整定PID参数的流程图如图5所示。

3 实验结果与分析

本文研究的对象选用NACA2412翼型，其旋翼与倾转翼的安装角为2°，直升机模式飞行时，旋翼垂直向上，此时倾转翼迎角为88°，固定翼模式飞行时倾转翼迎角为2°，故倾转翼飞机过渡段即为倾转翼迎角由88°变化到2°的过程。为了简化过渡过程，本文假定倾转翼迎角匀速变化，经过9 s左右由88°转到2°，如图6所示，建立的倾转翼飞机过渡段控制系统仿真框图如图7所示。

本文首先采用手动调参的方式来整定PID参数，然后尝试在PID控制方法中引入遗传算法，利用遗传算法强大的全局搜索能力[15]，对PID控制器的參数进行整定，以找到全局最优的控制器参数，并将两种方法仿真结果进行对比分析，找出更优的控制方法。遗传算法整定PID的寻优结果如图8所示。

倾转翼飞机过渡段的初始状态为[u0，w0，q0，θ0，h0]，大小设置为[3，0，0，0，20]，期望高度设为20 m;遗传算法参数设置：种群大小设为100，进化代数为30，交叉概率为0.9，变异概率为0.1。旋翼拉力控制器最优KP，KI，KD分别为14.687 5，14.958 4，6.645 9，升降舵舵力控制器最优KP，KI，KD分别为14.489 6，7.656 3， 11.064 7。系统的仿真结果如图9所示。

可以看出，采用传统PID方法时，飞机高度曲线能够在期望的高度20 m附近衰减振荡，系统振荡频率过大，调节时间过长，其控制效果很不理想，无法满足控制要求。这是因为传统PID本身存在一定局限，其针对强耦合、非线性系统的控制，无法得到令人满意的控制效果，用试凑法来整定控制器参数，具有很大的偶然性，往往无法找到控制器参数最优值，从而导致控制结果不理想。而引入遗传算法对PID参数进行整定之后，倾转翼飞机在12 s左右达到期望高度20 m并保持稳定，并且超调量小于5%，能够基本满足控制要求。故采用遗传算法整定PID的控制方法能够更好地实现倾转翼飞机过渡段的定高控制。

由于过渡段前期速度不是很大，当倾转翼向前倾转时，会产生一个低头力矩，此时升降舵的作用不足以调整飞机姿态，所以飞机会有一个掉高的过程，随着倾转翼不断向前倾转，前飞速度不断增加，升降舵的作用也越来越大，升降舵向上偏转，产生一个抬头力，来抵消之前的低头力矩，将飞机的姿态调整回来。过渡段结束时，俯仰角有一定的稳态误差，这是因为此时的垂向速度不为零，即在机体坐标系z轴正方向速度不为零，此时通过升降舵上偏，产生向下的正舵力，使飞机产生一个正的俯仰角，以保证飞机高度不变。

4 结  论

由于倾转翼飞机过渡过程是一个时变过程，传统PID在整个控制过程仅采用一组固定的控制器参数，无法找到全局最优的控制器参数，显然无法满足整个控制过程的控制要求。针对这一问题，本文采用遗传算法优化PID参数，利用其全局寻优能力找到全局最优的PID参数，以提高控制器的控制效果，结果表明，基于遗传算法整定PID控制方法的控制效果明显优于传统PID控制方法，且可以基本满足过渡段的定高控制要求，对于此类时变、强耦合、非线性系统的控制具有一定的参考价值。总的来看，俯仰角和垂向速度变化曲线还存在一定的稳态误差，但很小，这可能是由于遗传算法本身的局限性造成的，可以尝试改进遗传算法或者与其他智能算法结合起来加以解决。

参考文献：

[1] Schaeffer J M，Cullen L M. Operating Procedures and Control Law for Transport Category Performance in the BE-LL-AGUSTA BA 609 Tiltrotor[C]∥American Helicopter Society Forum，2007.

[2] Kim B M，Kim B S，Kim N W. Trajectory Tracking Controller Design Using Neural Networks for a Tiltrotor Unmanned AerialVehicle[J].Journal of Aerospace Engineering，2010，224 （8）： 881-896.

[3] 陈永，龚华军，王彪.倾转旋翼机过渡段纵向姿态控制技术研究[J].飞行力学，2011，29（1）： 30-33.

Chen Yong，Gong Huajun，Wang Biao.Research on Longitudinal Attitude Control Technology of Tilt Rotorduring Transition[J].Flight Mechanics，2011，29（1）： 30-33.（in Chinese）

[4] Rysdyk R，Calise A J，Chen R T N.Nonlinear Adaptive Control of Tiltrotor Aircraft Using Neural Networks[C]∥World Aviation Congress，1997.

[5] 范和平，宋彦国，王焕瑾.基于QFT的倾转旋翼飞行器控制律设计[J]. 江苏航空，2017（1）： 2-8.

Fan Heping，Song Yanguo，Wang Huanjin.Design of Control Law for Tilt-Rotor Aircraft Based on QFT[J].Jiangsu Aviation，2017（1）：2-8.（in Chinese）

[6] Mehra R K，Prasanth R K，Gopalaswamy S.XV-15 Tiltrotor Flight Control System Design Using Model Predictive Control[C]∥IEEE Aerospace Conference，1998.

[7] Rysdyk R T，Calise A J.Adaptive Model Inversion Flight Control for Tilt-Rotor Aircraft[J].Journal of Guidance Control & Dyna-mics，2012，22（3）： 402-407.

[8] 夏青元，徐锦法，张梁. 倾转旋翼飞行器无模型自适应姿态控制[J].系统工程与电子技术，2013，35（1）：146-151.

Xia Qingyuan，Xu Jinfa，Zhang Liang.Model-Free Adaptive Attitude Controller for a Tilt-Rotor Aircraft[J].Systems Engineering and Electronics，2013，35（1）：146-151.（in Chinese）

[9] 史小明.倾转翼飞机过渡段纵向飞行控制研究[D]. 南昌： 南昌航空大学，2017.

Shi Xiaoming.Research on Longitudinal Flight Control of the Transition Section of Tilt-Wing Aircraft[D].Nanchang： Nanchang Hangkong University，2017. （in Chinese）

[10] 吴健健. 倾转翼飞机过渡段纵向飞行控制研究[D]. 南昌：南昌航空大学，2019.

Wu Jianjian.Research on Longitudinal Flight Control of Tilt Wing Transition Section [D]. Nanchang：Nanchang Hangkong University，2019.（in Chinese）

[11]刘阳. 倾转翼无人机倾转装置设计及过渡段特性研究[D]. 南昌： 南昌航空大学，2019.

Liu Yang.Design of Tilting Wing UAV Tilting Device and Characteristics of Transition Section[D]. Nanchang：Nanchang Hangkong University，2019.（in Chinese）

[12]Gani M M，Islam M S，Ullah M A.Optimal PID Tuning for Controlling the Temperature of Electric Furnace by Genetic Algorithm[J].SN Applied Sciences，2019，1（8）： 1-8.

[13]Abhishek Kumar Jha，Sovan Sundar Dasgupta. Fractional Order PID Based Optimal Control for Fractionally Damped Nonlocal Nanobeam via Genetic Algorithm[J].Microsystem Technologies，2019，25 （11）： 4291-4302.

[14]朱紅萍，罗隆福.基于ITAE指标的PID控制器参数优化设计[J]. 电气自动化，2009，31（6）： 37-39.

Zhu Hongping，Luo Longfu.Optimization Design of PID Controller Parameter Based on ITAE Index[J].Electrical Automation，2009，31（6）：37-39.（in Chinese）

[15]吴春梅.现代智能优化算法的研究综述[J].科技信息，2012（8）： 31.

Wu Chunmei.A Review of Modern Intelligent Optimization Algorithms[J].Science and Technology Information，2012（8）： 31.（in Chinese）

Height Control for Transition Flight of Tilting Wing

Aircraft Based on Genetic Algorithm Tuning PID

Zheng Guangting1，Wang Qi2*，Chen Longsheng2，Yang Longfei1，Wang Rong2

（1.School of Information Engineering，Nanchang Hangkong University，Nanchang 330063，China;

2.School of Aircraft Engineering，Nanchang Hangkong University，Nanchang 330063，China）

Abstract：Aiming at the characteristics of strong non-linearity and strong coupling of the dynamic characteristics of the tilting wing aircraft during the transition mode flight，the traditional PID control method is difficult to design its control parameters and achieve fixed height control. In this paper，genetic algorithm and PID control theory are combined，and the global optimal PID control parameters are obtained based on the genetic algorithm tuning to ensure a good fixed height control effect. The simulation test results show that the PID controlparameters are obtained by the genetic algorithm tuning can better achieve the fixed-height flight control of the tilting wing aircraft transition section.

Key words： tilting wing aircraft; transition; non-linearity; genetic algorithm; PID; flight control

收稿日期：2020-05-25

作者简介：郑光廷（1993-），男，安徽亳州人，硕士，研究方向是飞行器控制。

通讯作者：王琦（1963-），男，浙江东阳人，教授，研究方向为控制理论与控制工程等。E-mail： wangqi439@126.com