裂纹尖端张开角在飞机金属薄壁结构中的应用

鲁龙坤 庄茁 柳占立

摘要：本文回顾了裂纹尖端张开角（Crack Tip Opening Angle，CTOA）在飞机金属薄壁结构中的应用。主要回答了“为什么CTOA是一个有效的断裂参数”和“CTOA怎样估算工程结构的断裂过程”这两个问题。韧性断裂的微观机理为空洞的形核、扩展及合并过程，断裂过程区（Fracture Process Zone，FPZ）包含了上述过程。CTOA实际上是FPZ的整体表征，因此CTOA是一个有效的断裂参数。此外，CTOA准则是一个局部断裂准则，它并不关心FPZ以外区域的状态，这使得它能够估算金属薄壁结构的裂纹扩展过程。

关键词：CTOA；断裂过程区；薄壁结构；局部断裂准则；韧性断裂

中图分类号：V215.6文献标识码：ADOI：10.19452/j.issn1007-5453.2020.04.004

基金项目：清华大学“水木学者”计划（2019SM077）

为了保证飞机服役期间的安全，必须对飞机结构进行完整性分析，而剩余强度分析是结构完整性分析[1-3]的重要组成部分。此外，机翼、机身等飞机结构通常归属于金属薄壁结构，因此金属薄壁结构的剩余强度分析在飞机结构分析中占据十分重要的地位。

剩余强度分析的本质就是裂纹扩展过程的分析。金属薄壁结构通常由低强度、高韧性材料组成，并且结构整体处于平面应力状态（厚度较小）。因此，这类结构的裂纹扩展过程具有以下特点[4]：（1）裂纹尖端的塑性区比较大，小范围屈服条件不再满足；（2）裂纹在结构失效之前发生了较大范围的扩展。由于塑性区比较大，基于线弹性断裂力学的评估方法不再适用，必须采用弹塑性断裂参数对结构进行评估。

常用的弹塑性断裂参数主要有J积分与裂纹尖端张开位移（Crack Tip Opening Displacement，CTOD）两种[5-6]。其中，J积分的推导前提为弹塑性材料的本构关系由非线性弹性材料的本构关系代替，如图1所示，上述前提要求载荷不发生卸载。当裂纹在金属材料中扩展时，裂纹尖端的载荷必然会发生卸载，卸载区的范围与裂纹扩展量正相关。换句话说，当裂纹具有较大范围的扩展时，J积分不再适用。因此，CTOD及其演化而来的裂纹尖端张开角（Crack Tip Opening Angle，CTOA）成为估算大范围屈服结构长距离裂纹稳态扩展的首选断裂参数[4]。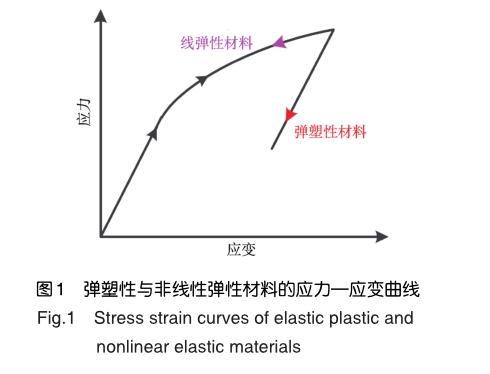

CTOD/CTOA是衡量裂纹尖端变形的参数，该参数与裂纹尖端区域以外结构的变形关系不大。此外，弹塑性裂纹的稳态扩展过程实际上就是裂纹面的形成过程，CTOA的局部特性与断裂的局部本质不谋而合。上述性质使得CTOD/CTOA（尤其是CTOA）準则在过去40年间取得了成功，它成功估算出了单裂纹试样[7]、多裂纹试样[8]、单裂纹加筋试样[9]、多裂纹加筋试样[10]，以及机翼/机身/全机等结构的剩余强度[11]。

CTOA及其应用也具有限制条件，并且CTOA参数的内在机理亟待进一步研究。本文将对CTOA的特点及其需要面对的问题进行总结，并侧重于阐述CTOA在金属薄壁结构中的应用。

1裂纹尖端张开角

1.1断裂参数

断裂的实质是材料发生分离，这一结果使得材料的连续性假设不再有效，因此连续介质力学本身不足以描述断裂现象，需要额外引入描述断裂现象的参数，这些参数就是断裂参数。

有效的断裂参数必须在一定的条件下具有通用性，即从一种几何构型获得的断裂参数临界值可以应用到另一种几何构型。基于上述思路，断裂参数必然经历两个阶段：产生阶段与应用阶段。图2给出了上述两个阶段。

顾名思义，生成阶段是指断裂参数的提出阶段。这一阶段包含如下步骤：（1）提出缺陷的理想模型；（2）寻找描述缺陷局部状态的物理量，这些物理量就是潜在的断裂参数。这些断裂参数的有效性将通过应用阶段验证。由于断裂参数的临界值在一定程度上反映了缺陷的临界状态，应用阶段的核心思路为由一种构型获得的临界断裂参数估算另一构型的裂纹扩展行为。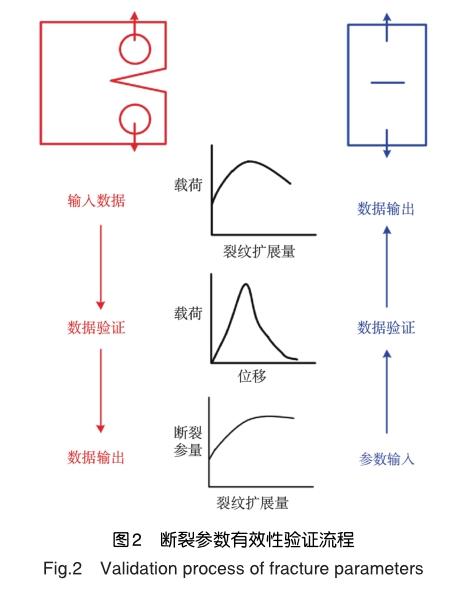

1.2 CTOA的定义

CTOA是指裂纹面的夹角[12]，它有工程与数学两个常用的定义。由于CTOA的工程定义便于应用数学定义从而便于理论分析，因此有必要对CTOA的两个定义都进行介绍。CTOA的工程定义为裂纹尖端后特定距离d处的裂纹面张开位移与距离d的比值：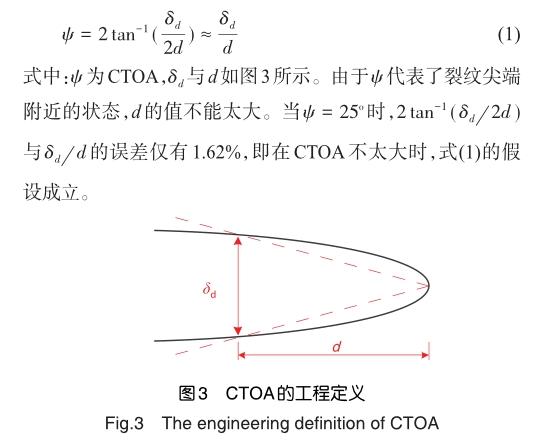

当裂纹扩展时，裂纹尖端处于临界状态，此时的CTOA即为临界CTOA（ψcr）。由于真实的裂纹面不是平面，d值的不同可能会导致不同的临界CTOA。针对上述问题，美国国家航空航天局（NASA）分别采用0.5mm、1.0mm、1.5mm的测量位置（d值）测量了铝合金2024-T351的临界CTOA（材料厚度分别为1.0mm、1.6mm、2.3mm）[13]，德国GKSS分别采用0.25mm、0.5mm、0.75mm、1.0mm、1.5mm的测量位置（d值）测得了铝合金5083 H321的临界CTOA（厚度为3.0mm）[14]。他们得出了相同的结论：（1） d值越小，临界CTOA数据点越发散；（2）数据点的平均值与d值无关。

由于真实裂纹面的曲折性[6]，结论（1）并不难理解，而结论（2）的唯一解释便是：裂纹尖端附近的裂纹面可以等效为一个三角形，如图4所示。

上述解释得到了GKSS的证实[14]，他们的试验表明：当裂纹扩展量Δa不太大时，临界CTOA等于δ5-Δa曲线的斜率。因此：

1.4 CTOA与裂纹扩展驱动力

最近，鲁龙坤等[28]从理论上证明了“为什么CTOA是一个有效的断裂参数”，其论证过程如下：

首先，裂纹扩展问题的本质是裂纹面的形成问题，有效的断裂参数必须能够表征这一过程。对于单位厚度试样，假设形成裂纹面所消耗的功率为Pcrack，这个功率可以看作一个力FT乘以一个速度。如果将这个速度取为裂纹尖端扩展速度a？，就好像在裂纹尖端施加了一个力一样，这个力推动着裂纹尖端向前移动，这个力就是裂纹扩展驱动力。有效的断裂参数必然与FT相关：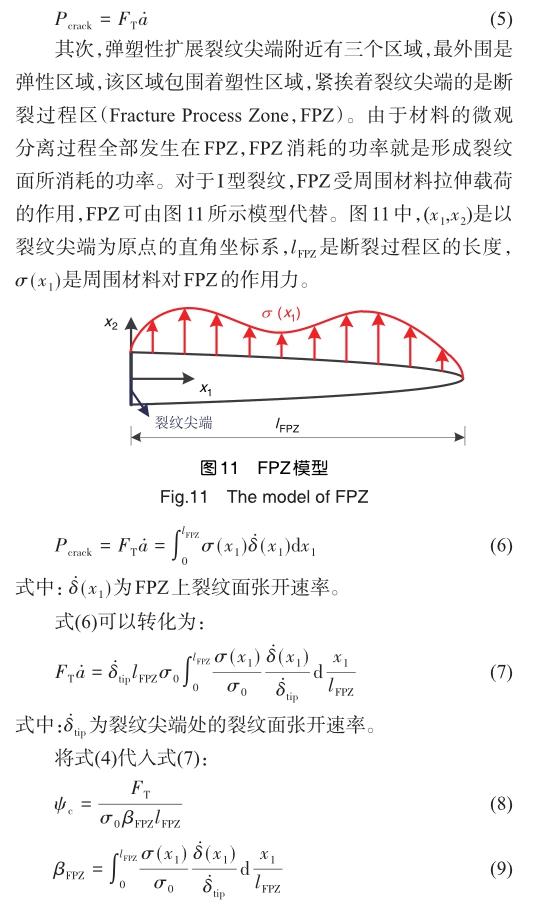

βFPZ是一个只取决于FPZ内材料微观破坏机理的参数。因此，CTOA等价于裂纹扩展驱动力，CTOA是一个有效的断裂参数。

2临界CTOA在薄壁结构中的应用

金属薄壁结构的面内几何通常大于4倍厚度，因此临界CTOA非常适用模拟金属薄壁结构中裂纹的扩展行为。本节总结了CTOA准则预测薄壁结构断裂过程的基本流程。

2.1基本思路

CTOA准则应用的基本思路为“裂纹扩展驱动力等于裂纹扩展阻力”。扩展驱动力指CTOA与几何构型的关系，扩展阻力就是临界CTOA，如1.4节所述，临界CTOA取决于FPZ内材料的微观破坏机理，当几何构型对FPZ没有影响时，临界CTOA只取决于材料及厚度。

CTOA估算断裂过程的步骤[12]如下：

（1）进行单轴拉伸试验，精确获得材料的应力—应变曲线。

（2）按照ASTM E2472或者ASTM E3039进行相应的断裂试验，测量材料的临界CTOA值以及记录试样的稳态扩展过程数据点；这一步骤需要注意以下几点：试验测量的临界CTOA值往往具有±0.5o～±1.5o的波動；试验件与真实结构应该具有相同的材料、厚度；试验件在达至剩余强度前具有显著的稳态裂纹扩展（即试样足够大）。

（3）进行2D/3D建模，采用节点释放法、临界CTOA值模拟试验件的裂纹扩展过程；由于模型与真实试验件的差异，临界CTOA试验值可能不足以重现试验结果，这时需要对临界CTOA进行上下微调使得模拟结果尽可能吻合试验结果；这一步骤需要注意以下几点：裂纹尖端附近的区域是三轴应力状态，当采用2D模型时，采用平面应变核模型（见图12）；为了避免额外的误差，模型与试验的d要相同；为了增强模型的自信心，可以先大概估算一下材料临界CTOA值的范围，然后在试验前对试验件进行盲估。

（4）对真实结构进行有限元建模，运用步骤（3）校正的临界CTOA对结构进行分析；这一步需要注意的是：试验件与真实结构的有限元模型在裂纹尖端应该具有相同的单元尺寸；试验件与真实结构应该采用相同的建模方法（3D、2D或者平面应变核模型）。

上述步骤的实质是通过有限元计算裂纹扩展驱动力ψ，并根据ψ=ψcr判断裂纹是否扩展。通过将扩展裂纹张开轮廓等效为静态裂纹张开轮廓减去塑性尾迹区轮廓（见图13），鲁龙坤等[29]理论计算出了裂纹扩展驱动力ψ，他们的步骤为：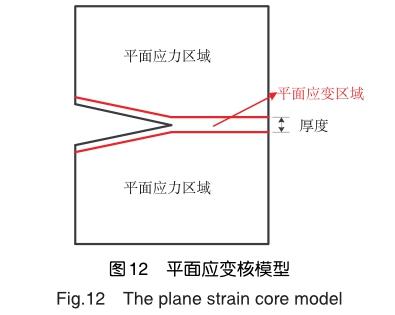

（1）假设塑性尾迹区的高度是一种裂纹扩展阻力曲线，该曲线只取决于应力状态与材料属性；其中，塑性尾迹区的高度等于真实裂纹尖端在临界状态下的CTOD（考虑了塑性区）。

（2）根据ASTM E2472对M（T）或C（T）进行断裂试验，进而获得塑性尾迹区的高度。

（3）应用线弹性理论或者非线性弹性理论获得结构静态裂纹的张开轮廓，该轮廓值减去塑性尾迹区的高度即为驱动力ψ。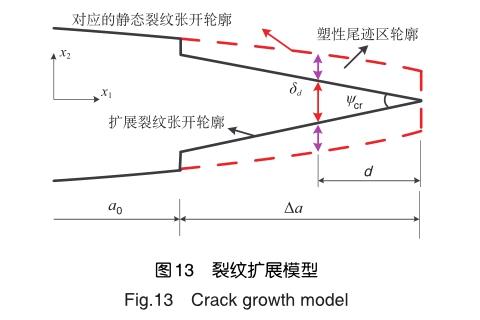

有限元方法的优点为：（1）适用于加筋板等复杂的薄壁结构；（2）可以考虑裂纹扩展的3D状态；（3）可以同时分析多条裂纹的扩展。有限元方法的缺点为：（1）建模过程、模型计算耗时耗力；（2）试验获得临界CTOA有较大的波动，临界CTOA值的调试需要操作人员具有丰富经验；（3）模拟过程是唯象的，不利于理解现象本质。

解析方法的优点为：（1）操作简单，只要将结果代入公式即可；（2）有利于CTOA准则指导手册的编写；（3）有利于理解现象的本质。解析方法的缺点为：（1）采用了还不成熟的假设，即“塑性尾迹区的高度是一种裂纹扩展阻力曲线”；（2）不适用于复杂结构；（3）不适用于多条裂纹的同时扩展。

2.2铆接加筋板

铆接加筋板是常见的飞机结构，该结构壁板上的裂纹不会扩展至筋条之上，筋条可以看作是一种几何约束，因此筋条仅影响裂纹扩展驱动力，2.1节的方法直接适用。

NASA与美国联邦航空局（FAA）对含有多部位损伤（Multiple Site Damage，MSD）的铆接加筋板进行了断裂试验[11]，并应用CTOA准则对加筋板进行了预测。壁板与筋条的几何构型如图14所示，其中壁板由2024-T3组成（厚度为1.6mm），筋条由7075-T6组成（厚度为2.2mm），壁板前后均具有筋条，中央筋条由主裂纹切断，且主裂纹前分布有MSD。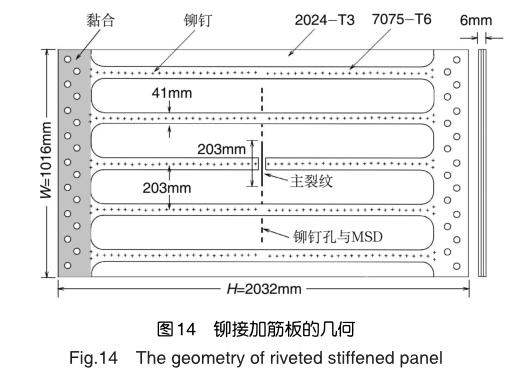

NASA的估算过程如下：（1）测量2024-T3、7075-T6的应力—应变曲线，并测量了厚度为1.6mm的2024-T3的临界CTOA，试验件为M（T）试样（增加了防屈曲装置），d为1mm，测量值为5.15o±1.0o。（2）应用2D壳单元模型模拟了试验件的断裂过程。经过反复调试，发现平面应变核模型的结果与试验结果吻合很好，其中平面应变核高度为2mm、临界CTOA为5.4o。（3）运用第二步的平面应变核模型模拟了铆接板的裂纹扩展过程，如图15所示。

2.3整體加筋板

整体加筋板的裂纹扩展具有两个特点：（1）壁板裂纹经过筋条时会分叉为两条裂纹，一条沿着壁板继续传播，另一条沿着裂纹扩展（见图16）。裂纹分叉的过程十分复杂，需要采用3D有限元进行模拟，模拟过程如图17所示。（2）壁板的厚度会发生变化，并且壁板与筋条的厚度也可能不同。结构具有几个厚度就需要几个对应的临界CTOA值，如图18所示。

除了上述两个特点，整体加筋板的模拟过程与铆接加筋板相同。NASA对图19所示剖面的整体加筋板进行了断裂试验[30]，加筋板的材料为2219-T81；然后NASA应用2.2节的方法对其裂纹扩展过程进行了模拟。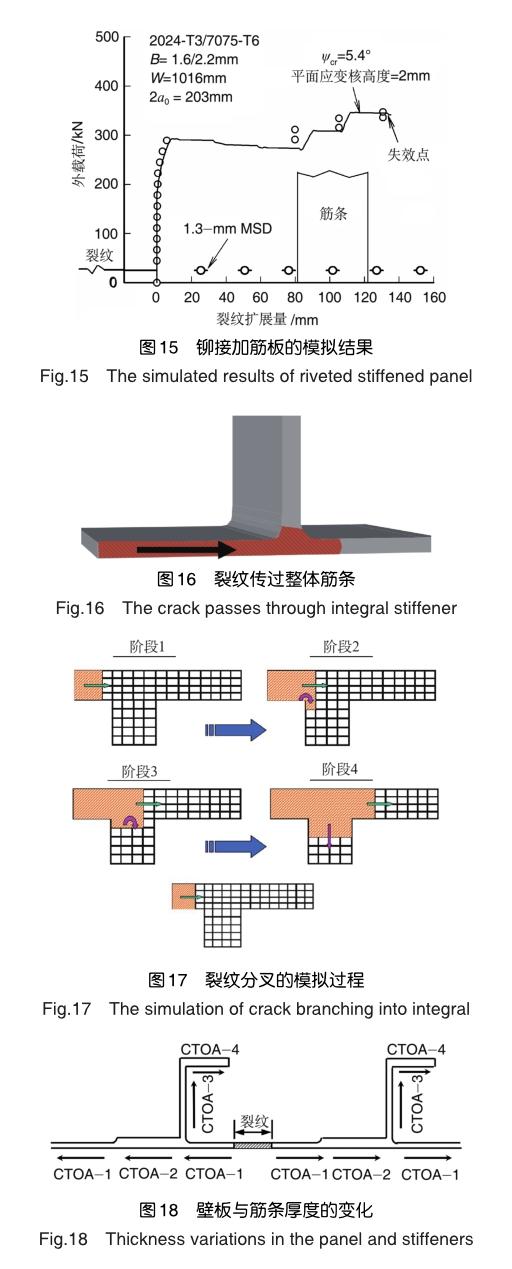

模拟结果如图20所示，当裂纹穿过筋条时，真实的结构已经失效，但是有限元模型仍然可以模拟裂纹的继续扩展，这是因为临界CTOA仅是一个局部参数，它并不关心裂纹尖端以外的区域，因此临界CTOA并不能判断结构的失效点。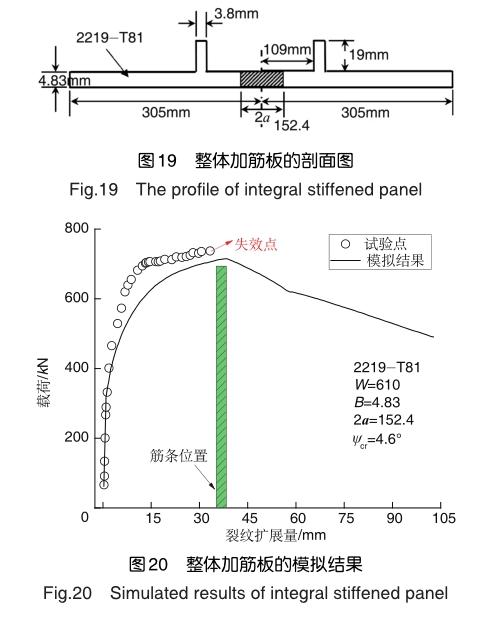

3结束语

裂纹扩展实质上是一个局部行为，它的结果就是裂纹面的形成。换个角度来讲，裂纹扩展过程就是“裂纹尖端处的扩展驱动力”等于“裂纹尖端处的扩展阻力”的结果，以此为思想，CTOA准则能够预测复杂结构的裂纹扩展过程。

假设一个含裂纹弹塑性体，裂纹在外载荷的作用下发生扩展。这一过程可以表述为：外力施加功，外力功流入裂纹尖端的部分就是裂纹扩展驱动力；当流入裂纹尖端的外力功足以形成新的裂纹面时，裂纹就会扩展，形成新的裂纹面所需的能量就是裂纹扩展阻力；外力功与流入裂纹尖端部分的差值取决于材料属性、几何构型，这一部分直接决定着结构的承载能力。

因此，断裂过程的研究有两个方向：（1）材料的本构关系研究；这一部分主要包括材料的破坏机理、材料塑性变形等耗能机制。（2）几何构型对裂纹扩展驱动力的影响；边界条件对裂纹尖端状态的影响、多裂纹的相互影响、筋条及屈曲对结构承载能力的影响等均属于这一部分。

参考文献

[1]吴富民.疲劳强度在航空工业中的应用[J].航空科学技术，1994，4（1）：10-13. Wu Fumin. Application of fatigue strength in aviation industry[J]. Aeronautical Science & Technology， 1994，4（1）：10-13.（in Chinese）

[2]尚晓冬，孙秀文，王刚.损伤容限技术在飞行器结构设计中的应用[J].航空科学技术，2012，5（1）：52-55. Shang Xiaodong， Sun Xiuwen， Wang Gang. Application of damage tolerance technology in structure design of aircraft [J]. Aeronautical Science & Technology， 2012， 27（1）： 52-55.（in Chinese）

[3]刘旭.民用飞机桶段试验及结果分析[J].航空科学技术，2016，27（2）：53-59. Liu Xu. Civil aircraft barrel test design and data analysis [J]. Aeronautical Science & Technology， 2016， 27（2）： 53-59. （in Chinese）

[4]Zerbst U，Heinimann M，Claudio D D，et al. Fracture and damage mechanics modeling of thin-walled structures An overview[J]. Engineering Fracture Mechanics，2009，76：5-43.

[5]Kanninen M F，Popelar C H. Advanced fracture mechanics[M]. New York：Oxford University Press，1985.

[6]Anderson T L. Fracture mechanics：fundamentals and applications[M]. Fourth Edition. New York：CRC Press，2017.

[7]Dawicke D S，Sutton M A，Newman J C，et al. Measurement and analysis of critical CTOA for an aluminum alloy sheet，NASA-TM-109024[R]. Hampton：NASA，1993.

[8]Xu W，Wang H，Wu XR，et al. A novel method for residual strength prediction for sheets with multiple site damage：Methodology and experimental validation [J]. International Journal of Solids and Structures，2014，51：551-565.

[9]Newman J C，Dawicke D S，Seshadri B R. Residual strength analyses of stiffened and unstiffened panels Part I：laboratory specimens[J]. Engineering Fracture Mechanics，2003，70：493-507.

[10]Seshadri B R，Newman J C，Dawicke D S. Residual strength analyses of stiffened and unstiffened panels Part II：wide panels[J].EngineeringFractureMechanics，2003，70：509-524.

[11]Chen C S. Crack growth simulation and residual strength prediction in thin shell structures[D]. Ithaca：Cornell University，1999.

[12]Newman J C，James M A，Zerbst U. A review of the CTOA/ CTOD fracture criterion[J]. Engineering Fracture Mechanics，2003，70：371-385.

[13]Dawicke D S，Newman J C，Bigelow C A. Three dimensional CTOA and constraint effects during stable tearing in a thin sheet material [R].ASTM STP，1995.

[14]Heerens J，Schodel M. On the determination of crack tip opening angle，CTOA，using light microscopy and deta5 measurement technique[J]. Engineering Fracture Mechanics，2003，70：417-426.

[15]ASTM E2472 Standard test method for determination of resistance to stable crack extension under low-constraint conditions [S].American Society of Testing Materials，2012.

[16]ASTM E3039Standard test method for determination of crack tip opening angle of pipe steels using DWTT specimens[S].American Society of Testing Materials，2016.

[17]James M A，Newman J C. The effect of crack tunneling on crack growth：experimentsandCTOA analyses[J].Engineering Fracture Mechanics，2003，70：457-468.

[18]Lam P S，Kim Y，Chao Y J. The non-constant CTOD/CTOA in stable crack extension under plane-strain conditions[J]. Engineering Fracture Mechanics，2006，73：1070-1085.

[19]Shibanuma K，Hosoe T，Yamaguchi H，et al. Crack tip opening angle during unstable ductile crack propagation of a high pressure gas pipeline[J]. Engineering Fracture Mechanics，2018，204：434-453.

[20]Xu S，Bassindale C，Williams B W，et al. Comments on CTOA transferability in crack tip opening angle during unstable ductile crack propagation of a high pressure gas pipeline[204（2018）434-453] [J]. Engineering Fracture Mechanics，2019，214：335-338.

[21]Mahmoud S，Lease K. The effect of specimen thickness on the experimental characterization of critical crack-tip-opening angle in 2024-T351 aluminum alloy[J]. Engineering Fracture Mechanics，2003，70：443-456.

[22]Mahmoud S，Lease K. Two-dimensional and three-dimensional finite element analysis of critical crack-tip-opening angle in 2024-T351 aluminum alloy at four thicknesses[J]. Engineering Fracture Mechanics，2004，71：1379-1391.

[23]Lu L K，Wang S N. Relationship between crack growth resistance curves and critical CTOA [J]. Engineering Fracture Mechanics，2017，173：146-156.

[24]Newman J C，Crews J H，Bigelow C A，et al. Variations of a global constraint factor in cracked bodies under tension and bending loads [R].ASTM STP，1995.

[25]Lu L K，Wang S N.Asimple model to explain transferability of crack tip opening angle[J]. Engineering Fracture Mechanics，2018，193：197-213.

[26]Johnson W M，James M A. A relationship between constraint and the critical crack tip opening angle[R]. NASA-CR-215930， 2009.

[27]Zhen Y，Tian H J，Yi H J，et al. Constraint-corrected fracture failure criterion based on CTOD/CTOA[J]. International Journal of Fracture，2018，214：115-127.

[28]Lu L K，Wang S N，Tong GR. Relationship between incremental J integral and crack tip opening angle in elastic plastic materials[J]. European Journal of Mechanics A/Solids，2019，75：399-409.

[29]Lu L K，Wang S N. An analytical method to predict residual strength based on critical CTOA[J]. Engineering Fracture Mechanics，2018，200：31-41.

[30]Seshadri B R，Tiwari S N. Residual strength analysis of monolithic structuresl[R]. NASATR 102051，2001.

（責任编辑王为）

作者简介

鲁龙坤（1992-）男，博士，助理研究员。主要研究方向：固体力学、断裂力学、材料力学。

Tel：010-62773780

E-mail： lulongkun@mail.tsinghua.edu.cn

庄茁（1952-）男，博士，教授。主要研究方向：固体力学、飞行器结构力学、断裂力学和非线性有限元的研究。

柳占立（1981-）男，博士，副教授。主要研究方向：计算固体力学、复合材料力学、断裂力学。

CTOA Applications in Metallic Thin-walled Structures of Airplane

Lu Longkun*，Zhuang Zhuo，Liu Zhanli

School of Aerospace Engineering，Tsinghua University，Beijing 100084，China

Abstract： The application of Crack Tip Opening Angle （CTOA） in metal thin-walled structures is reviewed in this paper. It answers "Why CTOA is a valid parameter" and "How to estimate fracture processes of engineering structures by CTOA". The micro mechanism of ductile fracture is the nucleation， growth and coalescence of void damage， which are included into the Fracture Process Zone （FPZ）. CTOA is in fact a representative of the FPZ， and thus CTOA is a valid fracture parameter. In addition， since CTOA criterion is a local fracture criterion， the CTOA parameter doesnt care whats going on outside of FPZ. That is why this parameter can estimate the crack growth process in metallic thinwalled structures.

Key Words： CTOA； fracture process zone； thin-walled structures； local fracture criterion； ductile fracture