快速出警的派出所最优选址模型研究

刘一恒 李文武

摘要：为满足快速出警的要求，研究派出所如何进行最优选址的问题。结合人口、距离2个参数引入“警民有效距离”的新概念，以警民有效距离最短和建设数量最少的派出所为目标函数，建立快速出警的多目标派出所最优选址模型，利用floyd算法构建居民区之间的最短邻接距离矩阵，并借助lingo软件求出某县城派出所选址算例的最优规划方案，验证了所建模型的有效性和可行性。

关键词：派出所选址;快速出警;最小成本;警民有效距离

中图分类号：D631.41文献标志码：A

文章编号：2095-5383（2020）04-0058-05

Study On Optimal Location Model of Police Station for Rapid Police Dispatch

LIU Yiheng，LI Wenwu

（School of Electrical and New Energy， Three Gorges University， Yichang 443002， China）

Abstract：In order to meet the requirement of dispatching police quickly， the problem of how to optimize the location of the police station was studied in this paper. Combining the two parameters of population and distance to introduce a new concept of “effective distance between police and civilians”， and taking the shortest “effective distance between police and civilians” and the minimum “number of construction” as objective functions， a multi-objective optimal location model of police station for rapid police dispatch was established.The floyd algorithm was used to construct the shortest adjacency distance matrix between residential areas， and the lingo software was used to find the optimal planning scheme for the site selection case of a county police station， which verifies the validity and feasibility of the built model.

Keywords：

the location of the police station; rapid police dispatch ;minimum cost; effective distance between police and civilians

随着我国城市化进程的加快，城市治安建设规划问题凸显。开展城市治安建设规划研究，尤其是对作为治安管理核心机构的派出所的选址研究具有重要现实意义。针对派出所选址问题，目前国内有很多学者作了积极探索，王春梅等[1]发现我国西部派出所布局规划的建设中存在不合理（一般都选在乡镇党委政府镇点），并且因派出所设置过多，导致难以发挥整体战斗力、成本高等问题;刘玉清[2]提出派出所选址方案需要综合考虑辖区面积、人口及其分布、治安状况等因素;孙庆珍等[3]提出城市应急设施选址要考虑“时效性原则”和“成本最小化原则”等。这些探索成果为我国城市治安建设规划提供了一定的思路。但由于这些探索大多只是借助抽象的定性分析来规划选址目标，因而导致了派出所选址缺乏科学依据而频繁搬迁、没有合理规划派出所数量出现成本的浪费、治安居民区划分不当等问题，无法实现有效的治安保障。因此，开展基于派出所最优选址问题的定量研究，构建派出所最优选址数学模型，通过定量科学计算来制定派出所选址规划非常必要。本文基于目前研究的不足和现实的需求，建立快速出警的派出所最优选址模型，并进行算例研究。

1 派出所选址模型

1.1 模型解决的问题

1）使派出所设点数量最少（成本最小化）;2）在规定的平均出警时间内完成快速出警;3）合理科学地划分派出所辖区。

1.2 模型的假设

本文提出如下假设：1）任意派出所与居民区的距离可通过调查或者计算得到;2）假设由于派出所建设与维護成本较高，故个数要有限制;3）假设每一居民区最多只能由一个派出所服务。

1.3 警民有效距离的引入

文献[2]以人口及其分布等为选址重要考虑因素，即核心思想是把派出所设立在人数尽可能多的地方，且兼顾如何满足周围居民区到该派出所距离最近。基于此，本文主要结合2个参数：该居民区的人数、居民区到派出所的距离，引入一个自定义的新概念——警民有效距离。

1）归一化处理

由于人数与距离的量纲存在差异，不便于直接运算，因此首先进行去量纲归一化处理。

居民区人数的归一化处理：

P*j=Pj-PminPmax-Pmin

其中：Pj表示第j个居民区的人数;P={P1，P2，P3，…，Pj}表示j个居民区人数的集合;Pmin表示P集合中最少的居民区人数;Pmax表示P集合中最多的居民区人数。

居民区之间最短邻接距离的归一化处理：

D*j=Dj-DminDmax-Dmin

其中：Dj表示第j个居民区与其他相邻的居民区之间最短的距离;D={D1，D2，D3，…，Dj}表示j个居民区最短邻接距离的集合;Dmin表示D集合中最短的最短邻接距离;Dmax表示D集合中最长的最短邻接距离。

2）警民有效距离

Deqj=P*2j+D*2j

其中：Deqj为警民有效距离。

结合二维坐标距离公式可以得出警民有效距离Deqj，描述的是若第j个居民区作为派出所选址地点时警民联系的程度，每一个居民区都有在地理位置且人口数维持不变的情况下，是唯一确定的。

1.4 派出所选址规划模型的建立

本模型涉及2个决策变量：是否在某居民区建立派出所、以及派出所与居民区之间是否建立服务关系，即涉及2种不同情况，为了使2种情况统一在一个问题之中，所以采用整数规划的方法。

决策变量：是否在第j个居民区建立派出所Rj={0，1};位于第j个居民区派出所是否与第i居民区建立服务关系θij={0，1}（以上2个决策变量皆为1表示是，0表示不是）。

目标函数：

min∑Ni=1∑Nj=1Djeq×θij（1）

minM（2）

其中：Deqj为警民有效距离;θij（θij=1or0）表示若派出所选址在第j个居民区是否與第i个居民区建立服务关系（1表示是，0表示不是）;M表示建立派出所的数量。

约束条件：

∑Nj=1Rj=M（3）

其中：Rj表示是否在居民区j设置派出所（1表示是，0表示不是）;M表示建立派出所的数量;N表示居民区的数量。

θij≤Rj（4）

其中：Rj表示是否在居民区j设置派出所（1表示是，0表示不是）;θij（θij=1or0）表示若派出所选址在第j个居民区是否与第i个居民区建立服务关系（1表示是，0表示不是）。

∑Ni=1θij=1（5）

其中：θij（θij=1or0）表示若派出所选址在第j个居民区是否与第i个居民区建立服务关系（1表示是，0表示不是）。

∑Ni=1Dij1 000≤V×t60（6）

其中：Dij表示居民区j到居民区i的最短距离，m;V为警车的时速，km/h;t为规定的最多出警时间，min。

i， j∈{1，2，3，…，N}（7）

式（1）中表示努力实现派出所的选址尽可能使得总的警民有效距离最小，及联系程度最为紧密;式（2）中表示建立数量最少的派出所以降低成本。约束条件中，式（3）表示派出所的建设数量;式（4）表示每个居民区只能由一个片区的派出所服务;式（5）为0-1决策变量式;式（6）表示保证能在派出所在规定时间内出警抵达救援现场;式（7）表示居民区编号。

2 模型的算例分析

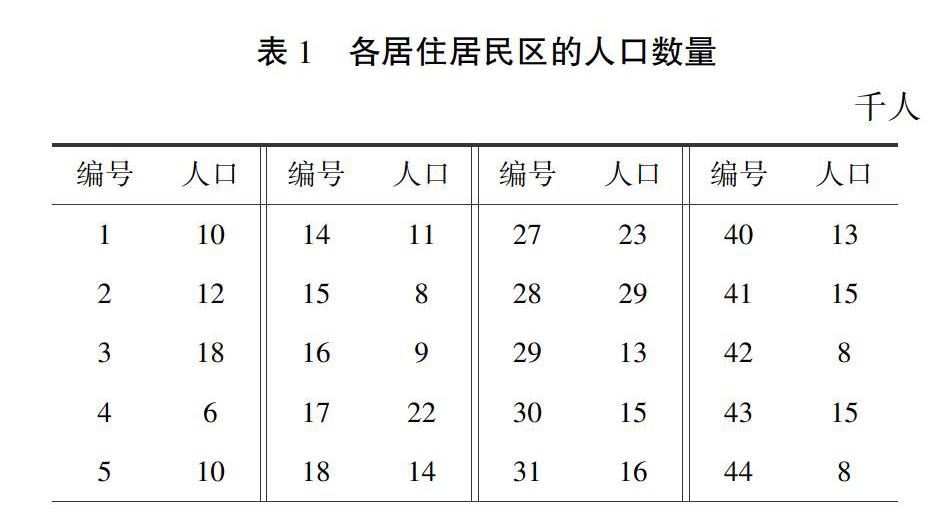
某县城共有52个居住居民区，各居住居民区的人口如表1所示。

现准备在此县城内建立若干个派出所，为每个派出所分配居民区，使在任意地点发生警情时，警察（警车时速为60 km/h）能在3 min以内到达事发地，如何策划派出所才合理，具体给出派出所的位置和个数。

2.1 模型的求解

由算例可知：模型参数县城居民区数N=52;警车时速V=60 km/h;规定出警时间t<3 min。

2.1.1 构建邻接矩阵和最短距离矩阵

1）构造邻接矩阵D

若居民区i与居民区j之间无直接连通的道路，则令（i， j）元素aij为∞;否则aij（i=1，2，…，52; j=1，2，…，52）为居民区i与居民区j实际连通的距离。

D=a11 a12 … a1na21 a22 … a2nan1 an2 … ann

由题给信息可知N=52，根据居民区与居民区之间的距离关系可以得到52×52的邻接矩阵U。

2）构造距离最短距离矩阵

规划方案均需标记实际居民区之间的分布情况矩阵，以及计算出居民区之间的最短距离矩阵以便解决问题。最短距离矩阵主要是由floyd算法实现。

floyd算法的原理就是从任意一条单边路径开始，所有亮点之间的距离是边的权（如果两点之间没有连接，则权无穷大）;对于每一对顶点u和v，检查是否存在一个顶点w使得u到w再到v的路径比已知的路径更短，如果是则更新。具体操作如下：

第一步，定义一个矩阵U用来记录插入点的信息，U[i， j]表示从i居民区到j居民区需要经过的点，初始化U[i， j]=j。

第二步，把各顶点逐一插入，比较插点后的距离与原来的距离，G[i， j]=min（G[i， j]，G[i，k]+G[k， j]），如果G[i， j]的值变小，则U[i， j]=k。

G中包含两点之间最短道路的信息，U中包含最短路径的信息。比如寻找节点V5到节点V1的最短路径，根据不断迭代，最后找出U[5，1]=3则说明节点V5到V1经过节点V3，路径为{V5，V3，V1}，而G中的数据则为对应最短路径的距离。

通过对k，i， j进行三重循环，最后可以循环输出最短距离矩阵：

D*=

0232426…625563452303748…70786427

63643950…3529213245276371…31253228

2.2 利用lingo软件进行规划求解

在lingo软件中，输入上述模型中的目标函数和约束条件即可进行规划。规划结果为：在此县城内可建立4个派出所，分别在第1、10、26、33号居民区，并据此将居民区划分为4个辖区，以保证派出所能够在规定时间（3 min）内及时抵达事发地点。派出所选址地和划分的辖区范围如图2所示。

3 结论

本文充分考虑居民区人口分布及居民区与居民区之间的道路连接情况，引入“警民有效距离”新概念，以设立最少的派出所（成本最小化）、最短的警民有效距离为目标，以派出所在规定时间快速出警等为约束条件，构建快速出警的派出所最优选址模型，提高了选址规划的科学性。

本文通过具体算例，使用floyd算法构建符合实际情况的邻接和最短距离矩阵，利用构建的模型求出快速出警的派出所最优选址方案，为定量分析派出所选址提供方法参考。

参考文献：

[1]王春梅，慕三英.我国西部农村公安派出所规划布局问题研究[J].江西公安专科学校学报，2006（2）：31-33.

[2]刘玉清.公安派出所规划建设模式探索[J].工程与建设，2009，23（4）：483-484，532.

[3]孙庆珍，李明，贾燕.基于多目标决策的城市应急设施选址问题研究[J].科技和产业，2014，14（6）：5-8.

[4]朱奇.基于多因素权重分析的输电线路灾害预警评估模型研究[D].武汉：武汉大学，2018.

[5]吴江宏.杭州市公安局巡逻指挥系统的设计与实现[D].成都：电子科技大学，2012.

[6]冯思兰.强化公安派出所的消防监督管理工作探讨[J].消防技术与产品信息，2011（12）：70-72.