浅谈高中生主动探究能力的培养

陈奕

[摘  要] 探究是创新的基础，是能力发展的核心，培养学生的主动探究能力是体现新课改下“以学为本”教育理念的好方法，也是高中数学教学研究的一大热点问题. 文章之中，研究者结合多年的教学实践提出以下培养举措：活用教学情境，激起探究欲望;探寻引导策略，预留探究空间;灵活变形手段，提升探究能力.

[关键词] 高中数学;主动探究;策略;培养

《普通高中数学课程标准》指出：需改变学生的学习方式，由被动接受式学习转变为主动探究式学习. 在教学实践中，学生解决问题能力的培养得到了一线数学教师的认可和落实，而主动探究能力的培养则没有得到足够的重视. 基于“自主、合作、探究”这种新型学习模式，体现了新课改下“以学为本”的教学理念，并确立了新型的师生关系，角色的转变促使当前数学教师需立足于“主动探究”这一新型模式，培养学生主动探究能力. 为此，本文结合多年的教学实践，谈谈培养高中生主动探究能力的举措，以期抛砖引玉.

■活用教学情境，激起探究欲望

培养学生的主动探究能力，首先需要培养兴趣，而具有诱发性的、生动性的教学情境是调动学习积极性的有效手段. 教师要活用教学情境，创设合理而有趣、科学而生动的问题情境，将学生的思维领入相关情境之中，使他们主动去探索和研究，从而加深对新知的掌握.

案例1：以“等差数列”的概念引入为例

问题1：某校报告厅有20排座位，这个报告厅每排座位数组成了这样一组数列：38，40，42，44，46，…你觉得这个报告厅在座位安排上有什么规律？

问题2：在统一鞋号中，每个成年女性的鞋子尺码（以“cm”为单位）以从大到小的顺序可以组成如下排列：25，24■，24，23■，23，22■，22，21■，21. 你觉得这种鞋子尺码的排列有什么规律？

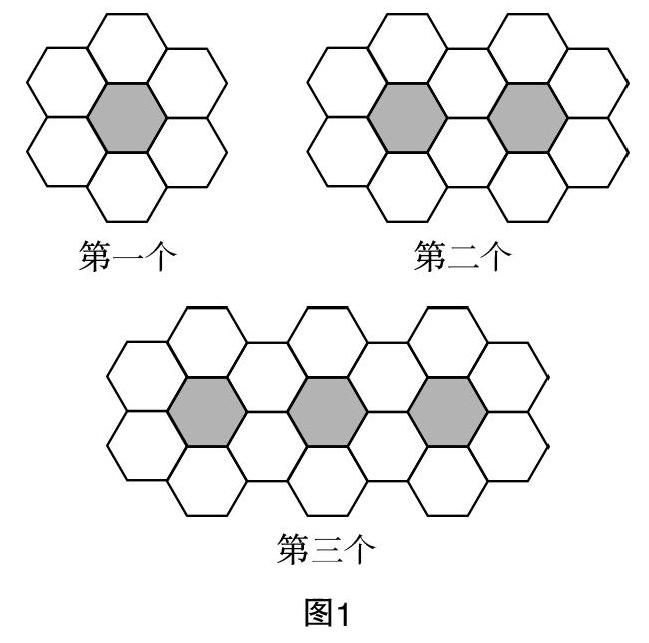
问题3：如图1，以蓝白两色的正六边形地砖按此规律拼图，你知道前3幅图中白砖的块数依次是多少吗？

成功的教学不是强制，也不是要求，而是一种积极主动的愿望，只有高涨的热情才能自觉投入到探究过程中去. 以上情境中看似“纷繁”的生活场景都隐约着“等差数列”的本质，从中逐步抽象出概念并提出数学问题自然而合理，在潜移默化中激起探究的欲望，培养用数学的眼光看世界的素养. 通过学生深入观察和实践操作，与原有认知冲突的新问题一步步地被挖掘出来，从而激发了探求性质的创造愿望.

■探寻引导策略，预留探究空间

事实上，无论是新课的展开，或是新知的构建，又或是新技能的形成，并非是教师对学生的要求或强迫，而应是在教师的引导下，学生主动进行探索的过程. 因此，教师需探寻到引导学生探究的策略，并预留足够的探究空间，鼓励、激励和诱导学生去自主探究，实现自主建构[1]. 这样一来，不仅可以为学生的全面发展创造广阔的空间，还可以为他们的终生发展奠定基础.

案例2：以“离散型随机变量的均值”的教学片段为例

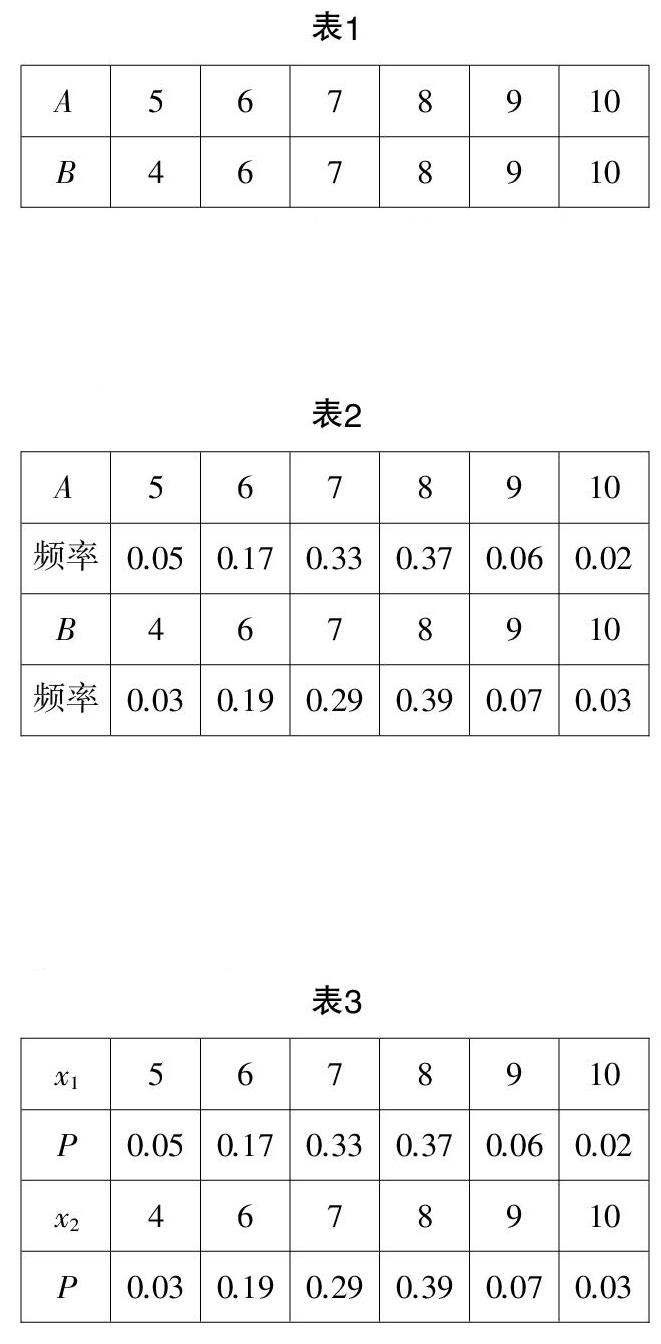
问题1：A，B二人进行了6次射击比赛，并得出以下成绩：

你觉得A与B谁的成绩更加稳定呢？

问题2：A，B二人进行了100次射击比赛，并得出以下成绩：

你觉得A与B谁的成绩更加稳定呢？

问题3：下表是A，B二人以往参加射击比赛的成绩汇总，其中x1是A的成绩，x2是B的成绩：

你觉得A与B谁的成绩更加稳定呢？

师：请大家合作交流，并解决以上问题. （经过独立思考和合作讨论，学生逐一解决了问题1和问题2，当解决到问题3时却思维卡壳，找不到解决思路）

师：大家先对比一下问题1和问题2，问题2和问题3，数据有何区别？并试着类比问题1和问题2的均值计算公式去解决你们无从下手的问题3. （学生很快投入到讨论和辨析活动中去了）

生1：我发现问题1中每人击中的环数各只出现了1次，问题2中每人击中的环数出现的次数不是1且各不相同，而问题3中每人击中的环数出现的次数没有规律.

生2：我觉得问题1中每人击中的环数的出现频率均是■，而问题2与问题3中，尽管都不相同，但前者表现在“频率”上，后者则是“概率”.

师：大家的观察都非常仔细，都能发现3个表格的区别在于频率与概率，那频率可否以概率来替代呢？

生3：在之前的学习中，曾经提及当实验的次数趋近于无穷时，一个事件发生的频率趋近于一个稳定值，该值即为这个事件发生的概率.

师：现在哪位学生可以来归纳一下它的概念呢？

生4：若随机变量X分布列入下表：

则可以称E（X）=x■p■+x■p■+…+xnpn为离散型随机变量的均值.

师：下面请从以上问题的均值计算公式进行比较，说一说随机变量的均值与算术平均值、样本均值有何区别，又有何联系;并试着举例说明，他们是否可以相同. 下面请各小组展开讨论. （学生又一次进行讨论）

……

以上3个问题的设计有效地将学生的注意力引入了主要的关注对象，并将一切不利于概括的因素均排除在外，此为引领学生展开自主探究的一种较好的教学策略. 纵观整个教学过程，不难看出，学生通过探究、讨论和交流，对以上3个问题的数据有了更好的甄别，自然关注到频率和概率的区别，得出二者的意义，跨越了本节课教学的难点. 在整个过程中，教师给学生预留了足够的探究空间，注重活动的思维性和有效性，帮助学生自然而然地完成探究，使其在头脑中不断进行“再创造”，做到真正意义上的“以生为本”[2].

■灵活变形手段，提升探究能力

随着教育课程改革的深化和素质教育的推进，传统教学中的照本宣科式教学模式已然遭到了学生的“遗弃”，课堂教学中的价值取向也逐步由“应试”转型为“能力”. 因此，在传授知识的同时，教师要有意识地灵活变形手段，自然渗入变式教学，开发学生思维的灵活性，让学生在自主探究中培养创新意识，使能力的培养得以落实[3].

案例3：三角函數最值问题

问题：已知函数f（x）=-■sin2x+sinxcosx，试求出f（x）在区间x∈0，■上的最小值.

变式1：已知函数f（x）=-■sin2x+cosx，试求出f（x）在区间x∈0，■上的最小值.

变式2：已知函数f（x）=■+■，试求出f（x）在区间x∈0，■上的最小值.

变式3：已知函数f（x）=■+■，试求出f（x）在区间x∈0，■上的最小值.

以上案例中，教师以“三角函数最值问题”中的一道典型问题为指引，很好地落实了学生的数学基础，并通过螺旋上升的变式练习，让学生在主动探究的过程中感受方法和知识. 教师在此要做的更多的是多角度、多层次去设计变式，让学生去思考、去观察、去发现、去联想、去探索，从而得出解决问题的策略，在活动中亲身领悟，优化解题方法，从而使探究精神和创新思维的培养落到实处.

总之，学习数学应该是一个积极主动的、生动活泼的、富有个性的过程，这里不仅需要学生从“要我学”转变为“我要学”，而且还需更进一步从“我要学”转型为“我会学”. 我们每位数学教师若能深入思考如何去适应新课标的要求，去培养学生自主探究的能力，引导学生用自己的“所有”去探究“所无”，通过自主探究学思考、学创新、学创造，使学生学会思考、学会探究、学会成长、学会发展，我们的数学课堂才是真正精彩的课堂.

参考文献：

[1]  谢月华. 让学生“探索”数学天地的“奥秘”——新课标下初中数学教学中探究性教学策略运用刍议[J]. 新课程（中），2012（09）.

[2]  张浩. 进步融于探究之中——刍议数学探究能力培养策略[J]. 理科考试研究（高中版），2013，20（07）.

[3]  任长松. 探究式学习：学生知识的自主建构[M]. 北京：教育科学出版社，2005.