改进的差分进化算法解决混凝土搅拌站选址问题

文/欧运娟

1 引言

作为一个建设型大国，中国对混凝土的需求与日俱增，现有的搅拌站已不足以支撑建筑的需要。例如2017年南宁市中心城区的预拌混凝土需求达到1400万立方米/年，要求搅拌站的总供应能力至少达到1960万立方米/年，而目前已有站点的总供应能力约为1380万立方米/年，存在很大的供应缺口。因此需要增加站点数量，并希望这些新增站点位于合理的位置，才能满足城市建设需要。

传统的选址问题涉及到的供应模式为“一对多”分配，属于整数规划问题。国内外许多学者对其进行研究并建立了一系列的模型和算法。与传统选址问题不同的是，搅拌站问题属于“多对多”分配模型。该问题的难点为站点向组团的分配量，即一个站点分配给一个组团的比例可以为0到1之间的任何实数，另一个难点是候选点的选择。当候选点数量众多时我们无法穷尽所有方案。常见的智能算法有蚁群算法、粒子群算法、遗传算法、差分进化算法等。DE算法作为一种新近提出的优化算法，引起国内外学者的广泛关注。但经典的DE算法对复杂优化问题容易出现早熟收敛。本文改进了经典的差分进化算法，增加了局部搜索，使其适用于搅拌站选址模型。

2 问题的描述与建模

2.1 问题分析

以2017年南宁市中心城区的搅拌站选址为例，研究如何选择新增站点，并尽量缩短混凝土的运输里其选址问题具有一些特殊性，主要体现在以下几个方面：

（1）双重规划目标。搅拌站选址的规划目标有两个：一是最小化混凝土的加权运输总里程（立方米·公里）；二是最小化新增站点数量。第一个目标可以缩短货物运输里程，从而减轻城市道路交通压力，减少车辆污染物排放。第二个目标不仅可以减少搅拌站对城市景观的影响，还有助于防范区域内搅拌站分布过于密集而出现恶性竞争。

（2）运输距离限制。由于预拌混凝土的使用具有很强的时效性，无法运送到较远的地方销售，因此在建模时应设定运输距离的上限。

（3）供应能力限制。单个混凝土搅拌站的规模不宜太大，实否则会造成规模不经济，大量车辆进出还会造成城市局部路段交通堵塞。

（4）新增站点数量是不确定的。在最大供应距离受限制的情况下，新增站点的数量取决于供需缺口的大小及候选站点、原站点和建设组团的空间分布有关。

（5）组团与搅拌站属于“多对多”的关系。即一个组团可以接受多个搅拌站的服务，一个搅拌站也可以供应多个组团。

2.2 符号说明

本文研究定义的集合、参数和决策变量说明如下：

2.2.1 集合

2.2.2 参数

demk为建设组团k的所需要的供应能力；dik为侯选站点ij与建设组团k的距离；djk为已有站点j与建设组团k的距离；td为混凝土运输距离的上限，td=25公里；newsi为候选站点i的供应能力，所有候选站点供应能力为50万立方米/年；oldsj表示原有站点j的供应能力，原有站点大部分的供应能力最大为170万立方米/年，供应能力最小的仅为32万立方米/年。

2.2.3 决策变量

2.3 建立模型

建立搅拌站选址的混合整数规划模型如下：

式（1）和（2）是目标函数，在满足需求的条件下，使货物运输总里程最小，同时要求新增站点数量尽量少。式（3）～（7）是约束条件，式（3）表示每个建设组团所需的供应能力都能得到满足，式（4）和（5）站点供应能力约束，式（6）为已有搅拌站均必须参与供应，式（7）表示运输距离不能砂于25公里。

2.4 经典DE算法

DE算法包括初始化、变异、交叉和选择四个步骤，其设优化问题为：

2.4.1 初始化

设种群规模为NP，问题维度为D。则第i个个体可以通过以下公式产生：

2.4.2 变异

对种群中的每个向量xi（目标向量），DE算法产生一个扰动向量vi。常用的变异公式如下：

2.4.3 交叉

其中，对于每个试验向量，均产生一个范围为[1,NP]的随机整数jrand，从而保证了在每一次迭代ui至少从vi获取了一个元素。

2.4.4 选择

DE的选择算子采用了优胜劣汰的策略。计算试验算子ui的目标函数值并与目标向量xi的目标函数值进行比较，并选择目标函数值小的个体进入下一代。选择操作如公式（16）所示。

3 改进的DE算法

上述混合整数规划模型虽然属于条件中位问题，常见的解决离散优化问题的启发式算法有遗传算法、蜂群算法、差分进化算法和蚁群算法等,本文算法在DE算法的基础上增加了局部搜索。

本文算法流程如下：

Step1：初始化种群规模NP，交叉率CR，收缩因子F。并初始化种群中所有个体；

Step2：计算每个个体的适应值，采用目标函数值作为适应值，计算f(xi)；

Step3：若当前最优解的适应值min(f(xi))低于xbest的适应值f(xbest)，则按当前最优解更新xbest；

Step4：按照公式（12）（15）（16）进行一次迭代；

Step5：如果满足规则，则执行局部搜索操作；

Step6：求出历史最优解xhbest；

Step7：如果算法达到最大评估次数，则退出；否则返回Step2。

3.1 编码

本文算法采用一个矩阵chr=（N+2）×M表示一个个体，其中M为最大站点数，N为组团数。增加的2行用来记录站点位置及剩余量。数组中前M行中的每个元素代表该列所在站点对该行所在组团的供应量，第M+1行的每个元素代表该列所在站点的位置，第M+2行的每个元素代表该列所在站点可供分配量。

3.2 种群初始化

种群中每个个体为问题的一个解，因此个体所包含的站点须满足所有约束条件。同时，为产生多样性的解，在选取站点时采用随机选取的方法。其步骤如下：

Step1：为每个个体chri随机选取M个站点，若chri包含所有原有站点，并且站点的总供应量大于总需求量，则进行Step2，否则返回Step1。

Step2：检查所有组团的分配量。若有组团的需求得不到满足，则随机选取一个未满足需求的组团，将站点分配给该组团。否则分配结束。

3.3 适应度函数：

此模型有两个优化目标，即最小化路径与其供应量的乘积的和（公式（1）），同时最小化新增站点的数量（公式（2））。因为新增站点数量规模不大，本文的算法将新增站点数量作为问题的输入。本文算法优化公式（1）。同时，我们将公式（1）作为算法的适应度函数。

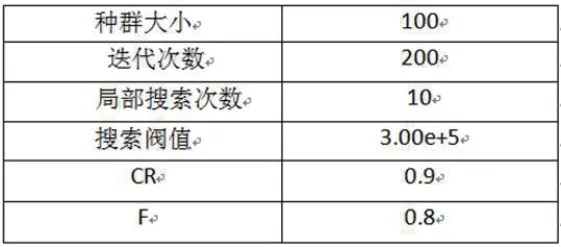
表1：参数设置

表2：算法性能对比

3.4 交叉

本文算法按照公式（12）进行交叉操作。子代产生过程的具体步骤如下：

Step1：随机产生交叉点a、b并按照公式（12）进行交叉，产生子代；

Step1：检查子代中重复的站点并进行替换；

Step1：检查交叉后产生的子代是否能满足需求，如果子代的供应量大于总需求量，则调整分配方案使每个组团的需求得到满足，否则不进行交叉操作。调整操作如下：

（1）遍历所有组团，如果该组团的供应量大于需求量，则将供应该组团的所有站点中路径最长的站点进行重新分配，直到该组团的供应量等于需求量。

（2）遍历所有组团，如果该组团的供应量小于需求量，则将需要从新分配的所有站点中路径最短的站点分配给该组团，直到该组团需求量得到满足。

3.5 局部搜索

针对搅拌站问题的特殊性，本文设计了两种变异方案。

（1）用未包含在个体中的候选站点随机替换包含在个体中的候选站点，为保证经过变异后的个体仍为模型的解，需要检查替换的站点是否满足组团的需求。如果不满足，则不进行变异。

（2）随机改变站点中的两条分配路径并调整方案，其步骤如下（假设li,n为站点i到组团n的路径）：

Step1：随机选取两条路径li,n、lj,m，假设路径li,n的供应量小于lj,m；

Step1：用路径li,m替换li.n，令两条路径的供应量相等；

Step1：增加一条路径lj,n，在只改变站点j供应量的条件下使所有组团的需求得到满足。

4 实验

以2017年南宁市中心城区的搅拌站选址为例进行模拟实验。实验数据包括8个组团，23个已有组团以及20个候选组团。参数设置如表1所示。

把基于DE算法的混合算法应用于南宁市城区混凝土搅拌站的选址问题，由于DE算法带有随机性，因此不能保证每次结果的一致性，但从结果看，该算法基本能控制在2.90e+5（米·万立方米/年）以内，显示了算法良好的稳定性。

表2给出了本文算法与GA算法、文化基因算法的性能对比，实验环境为独立运行30次。从表2可以看出，本文算法无论是最好结果或平均结果都要优于经典的GA和文化基因算法。

5 结论与展望

本文对混凝土搅拌站的选址问题尝试以新的思路来研究，在传统的差分进化算法基础上增加了局部搜索，提出了一种改进的差分进化算法。实验结果表明，该算法能稳定、有效地解决混凝土搅拌站的选址问题。

注[1]为了保障需求，供应能力与需求量的比例按1.4计算，则1400×1.4=1960万立方米/年。