再议函数极限求解的方法与技巧

李庆娟

（大连财经学院 辽宁 大连 116600）

极限是高等数学的重要概念和研究对象，它是高等数学的理论研究工具，贯穿于高等数学的教学的整个过程，因为高等数学中比较重要的概念都是通过极限来定义和研究的，可见它的重要性.可以说学好极限对高等数学后续内容的学习至关重要，因此极限是教学中的重点，也是各类考试重点考核的内容[1-3].在文献[4]中，本人曾介绍过极限的几种常见的求解方法，但不全面，在此基础上，我进一步地研究了函数极限求解的主要方法和技巧，总结归纳了共计13 种主要方法。

1.利用极限的四则运算法则求解函数极限

极限运算法则是继极限定义之后的一个主要内容，它是求解函数极限最基本的方法。

定理：设 1im(f(x)±)=A，1img(x)=B，则

（1）1im(f(x)±g(x))=1imf(x)±1img(x)=A±B；

（2）1imf(x)g(x)=1imf(x)·1img(x)=AB；

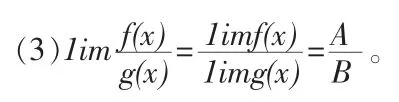
说明：①定理中“1im”表示自变量是同一变化过程，对自变量的任何一种变化趋势都成立，而且对数列极限也成立。

②注意应用四则运算法则求解极限的前提是f(x)，g(x)的极限都存在，否则不能用，且在商的法则中要求分母的极限不为零。

2.利用初等变形法求函数极限

除了利用极限的四则运算法则求解函数极限，那么求函数极限还有很多其他基本的求解方法，例如有理化方法、约分化简法、通分化简等等， 也就是在求解函数极限之前先将函数即极限式子进行初等变形，化成比较简单的形式，然后再求极限.当然，这个过程还是要用到极限的四则运算法则。

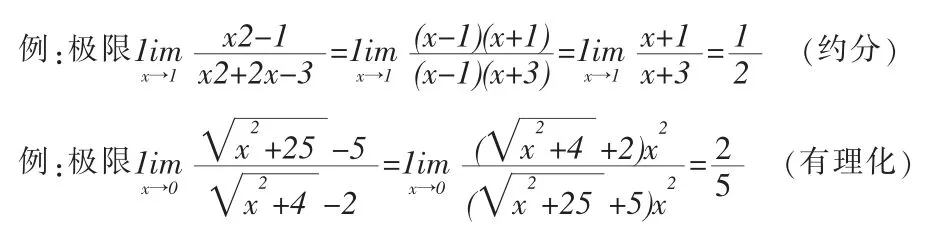
利用基本方法只能求而出简单形式的函数极限，因此我们需要进一步掌握更多的求解方法。

3.利用重要极限法求函数极限[4]

在高等数学的极限理论中，有两个重要极限，即

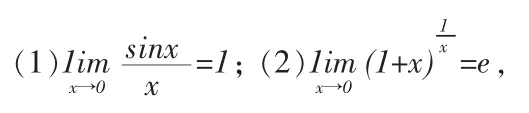
它们的应用非常广泛，很多类似的函数极限问题可以转化为重要极限来求解，为了更好地应用重要极限，我们必须要抓住两个重要极限的形式和特点，进而套用公式求解。

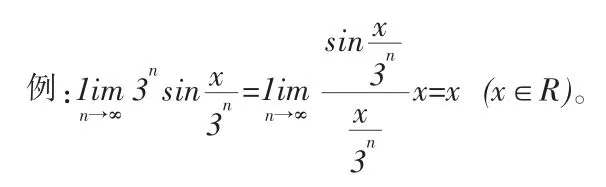
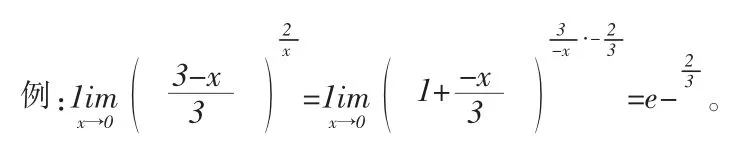
4.利用等价定理求函数极限

利用函数的极限等价定理求解极限也是在高等数学学习过程中需要重点掌握的一种方法。

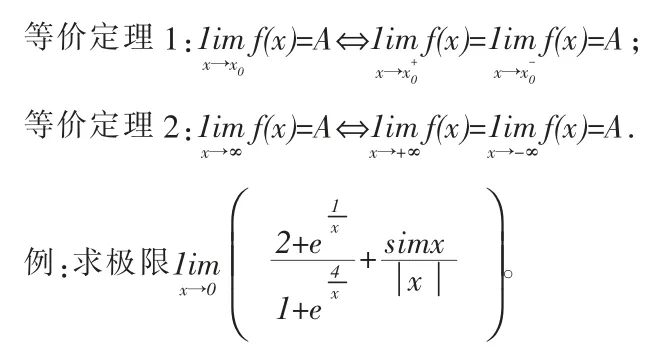
分析：极限式子的第二项的极限明显与左右趋近0 有关，故需要分左右极限讨论。

注：一般地，分段函数在分段点处的极限往往需要用等价定理讨论极限的存在性。

5.利用特殊结论求函数极限

当所求的函数极限满足：极限条件是x→∞而极限式是多项式比多项式时，就可以套用以下结论：

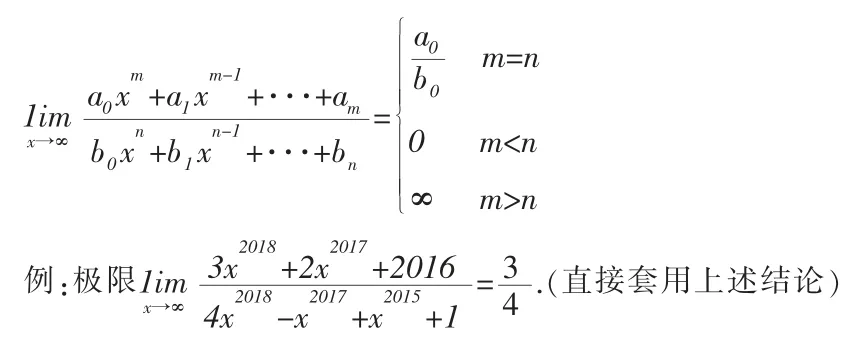
6.利用无穷小的性质求函数极限

无穷小量是极限为零的变量， 高等数学学习中首先要理解好无穷小量的概念，其次要掌握它的性质和应用，特别是无穷小量与有界函数的乘积仍然是无穷小量，这个性质通常用来求解相应的函数极限问题。

这里我们注意到函数cos(2x+1).当x→+∞时虽然极限不存在，但是它为有界函数，即又因为所以利用无穷小量的性质可知

7.利用等价无穷小替换法求函数极限

利用等价无穷小替换的方法求解函数极限是求解函数极限非常重要的一种方法，在应用这个方法时，往往要结合其他方法，例如洛必达法则等方法，从而使问题更快的求解出来.我们常用的等价无穷小量有：x→0 时：

（1）x～sinx～tanx～arcsinx～arctanx～1n(1+x)～ex-1；

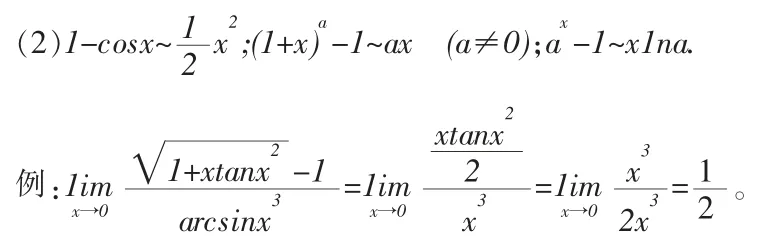
在利用无穷小量替换法求解函数极限时要注意：在乘积因子里可以直接替换成相应的等价的无穷小量，但是在代数和运算的式子里面尽量不要直接替换，否则就会出现错误。

8.利用洛必达法则求极限

洛必达法则是求解函数极限的非常重要而且也是很常用的方法，洛必达法则主要是涉及七个类型的函数极限求解问题，即七个类型，其中属于两个基本类型，其它的五个类型极限问题均可以通过化简变形转化成为基本类型求解.在利用洛必达法则求函数极限时往往需要结合等价无穷小替换的方法，这样能够使问题更快、更容易求解出来。

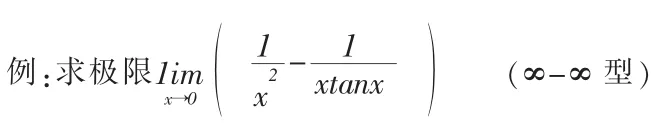
解：此题为∞-∞型，这种类型的极限通常采用通分方法将其化为基本型。

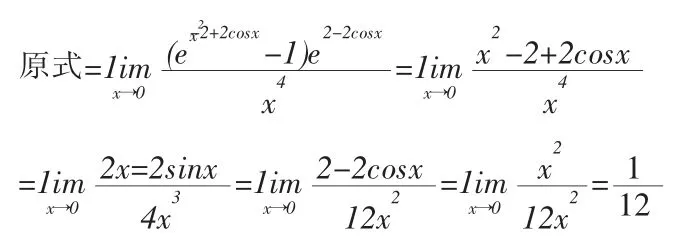
9.利用泰勒公式求函数极限

我们用泰勒公式求解函数极限时，主要是指带有佩亚诺余项的泰勒公式.常用的公式如下有：

注：此题在上面讲无穷小替换的方法时做过，当时直接等价无穷小替换就出现了错误，而这里用泰勒公式替换就对了，所以为什么强调在加减法的极限式子中不要轻易直接用常见等价无穷小替换，因为你找的可能不是此题的等价无穷小，否则会出错。

10.利用导数定义求极限

通过学习导数的定义，我们知道导数是通过极限来定义的，它是函数增量与自变量增量比值的极限，即变化率问题，所以遇到类似这样结构的极限就可以转化为相应导数问题求解。

11.利用变量代换法求极限

变量代换法也是求解函数极限的一种典型的方法，这里的变量代换主要是指直接代换和倒代换，尤其是倒代换比较常用，这种难度的题目一般在考研或是高等数学竞赛中较常见。

令 t=sinx,x=arcsint，则

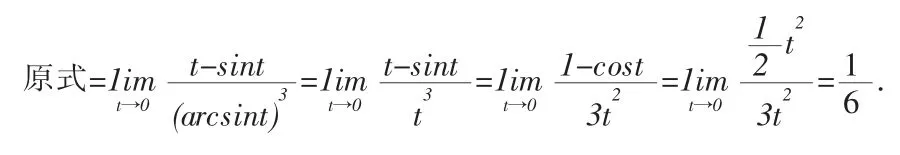
12.利用中值定理求极限

高等数学中所学的中值定理包括微分中值定理和积分中值定理，这里的所说的中值定理主要涉及的是微分中值定理中的拉格朗日中值定理，它的应用是非常广泛的，特别在求解函数极限时也很好用。

定理：设函数f(x)满足在[a,b]上连续，在(a,b)内可导，则在至少存在一点 ξ∈(a,b)，使得 f(b)-f(a)=f'(ξ)(b-a)。

在求解函数极限时，如果极限式子中出现f(b)-f(a)的形式，即函数增量问题，而且极限不好求解时，我们就可以考虑利用拉格朗日中值定理进行化简求解。

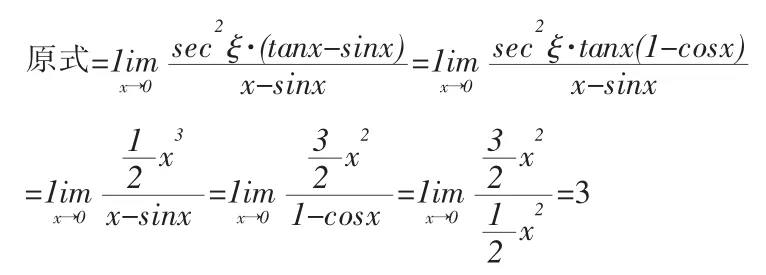
13.利用夹逼定理求极限

利用夹逼定理求极限是求极限的一个主要方法，特别是求数列极限时往往很奏效，但求函数极限相对用的少些，我们看看下面的例子。例：求极限

以上我们总结并归纳了求解函数极限的十三种主要方法和技巧，这些方法都是比较典型的方法.当然，求极限的方法还有很多，比如求数列极限时，还可以利用定积分的定义求解，利用单调有界数列必有极限准则求极限，利用级数的必要性求解等等方法.总之，求极限的方法很多，而且各有不同，这就要求我们在学习极限求解时，要善于总结归纳，只有熟练掌握了各种求解方法，遇到问题时，才能轻松求解出来，做到事半功倍。