基于层次分析—云模型的数学核心素养对学生综合能力培养的效果研究

孟旭东

摘 要：文章选取学习分析能力、批判创造能力和实践创新能力作为评价数学核心素养对学生综合能力培养作用的核心评价指标，结合所在学校的综合能力培养评估体系，构建基于层次分析法——云模型的数学核心素养对学生综合能力培养的数学模型。借助专家经验，对评价指标因素运用云模型描述，获得各评价量化值，利用层次分析法确定评价指标间相对重要性程度，确定评价指标的权重，分析数学核心素养对学生综合能力培养作用的效果。研究表明，大学生良好的数学核心素养对综合能力培养起到有效推动作用。

关键词：层次分析法;云模型;数学核心素养;综合能力

中图分类号：G642 文献标识码：A 收稿日期：2020-06-17 文章编号：1674-120X（2020）32-0051-02

2014 年3 月，教育部印发了《关于全面深化课程改革、落实立德树人根本任务的意见》，首次以文件形式提出“核心素养”的概念，把核心素养作为各学科的课程目标和教学要求的核心依据。2016年9月教育部发布的《中国学生发展核心素养》以科学性、时代性和民族性为基本原则，以培养“全面发展的人”为核心，分为三方面、六大素养、十八个基本要点。如何借助数学核心素养培养机制切实推动教学改革、有效培养学生良好的学习习惯、增强学生的学习能力、逐步提高学生的综合能力等成为高教研究的热点话题。

一、数学核心素养对学生综合能力培养评估模型

数学核心素养是培养大学生综合素质和创新精神的重要手段，可从学习分析能力、批判创造能力、综合实践能力等方面构建数学核心素养对学生综合能力培养作用的指标体系，量化指标，建立评估模型，进行综合评价，客观地认识数学核心素养对大学生综合能力培养的作用。这为数学核心素养培育的实施单位提供了科学合理的参考依据，以便完善素质教育培养机制，推动教学改革、增强学生的综合能力、提升素质教育质量。针对数学核心素养对学生综合能力培养过程的关键指标因素，可建立如下综合评估指标体系：

（1）分析概括能力，它是数学核心素养对学生综合能力培养体现的基本能力，主要包含理解知识能力、分析问题能力、文字表述能力和全局概括能力等。

（2）批判创造能力，它是数学核心素养对学生综合能力培养展示的核心能力，主要包括质疑权威能力、发现问题能力、发散思维能力和解决问题能力等。

（3）综合实践能力，它是数学核心素养对学生综合能力培养蕴涵的综合能力，主要包括沟通协调能力、融会贯通能力、团队协作能力和灵活运用能力等。

二、基于层次分析—云模型的数学核心素养对学生综合能力培养的效果研究

（一） 层次分析

层次分析由Saaty 教授提出，它是一种简便、灵活、实用的多准则决策方法，适用于复杂、模糊、随机实际问题的定量决策。主要内容是就数学核心素养对学生综合能力培养系统进行模型化处理，分析影响目标的因素，由基本属性建立层次隶属关系，构建指标因素层次数学模型。步骤为：

（1）基于目标层是通过一定的准则层约束方案层，同层次因素之间相互独立且互不影响，构建包含目标层、准则层和方案层的递阶层次模型。

（2）对递阶层次的各层指标因素进行两两比较以构造判别矩阵A=（aij）n'n，为使A定量化和无量纲化，采用1～9 标度法，具体含义为：

①重要性标度1表示：两因素相比，前者比后者同等重要;

②重要性标度3表示：两因素相比，前者比后者稍微重要;

③重要性标度5表示：两因素相比，前者比后者明显重要;

④重要性标度7表示：两因素相比，前者比后者强烈重要;

⑤重要性标度9表示：两因素相比，前者比后者极端重要;

⑥重要性标度2，4，6，8表示：分析因素介于相邻判断中间值。

（3）采用特征根法求A的最大特征值l（A）及特征向量w（A）=（w1，w2，…，wn）T，则A=（aij）n'n，其中aij =wi/wj，i，j=1，2，…，n。

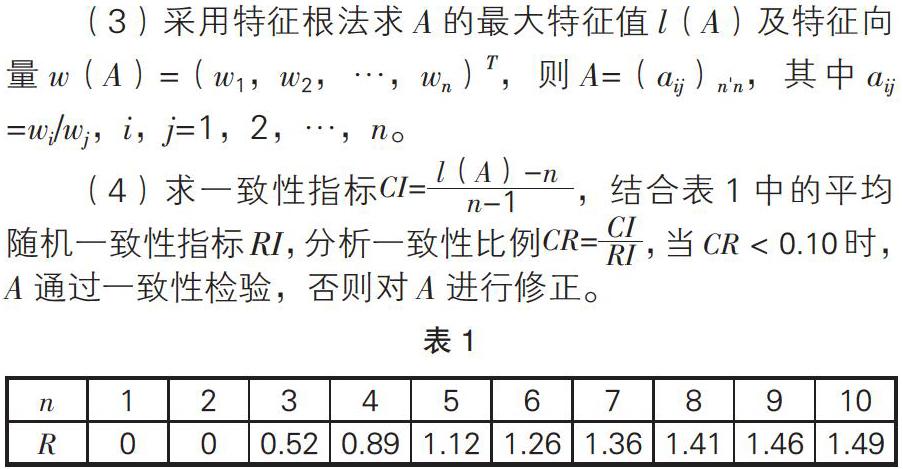
（4）求一致性指标，结合表1中的平均随机一致性指标RI，分析一致性比例，当CR<0.10时，A通过一致性检验，否则对A进行修正。

（二） 云模型

云模型由李德毅院士于1995年提出，建立在随机理论和模糊理论基础上，可实现定性与定量间的转化，能在系统评价与决策分析等方面发挥巨大作用，是处理复杂性、随机性、多属性问题的良好工具。本文采用“优”“良”“好”“一般”“差”的定性语言来描述数学核心素养培养在学生综合能力培养中的作用，用云模型来表达。

1.云模型的数字特征

云模型通过云的数字特征（期望Ex，熵En，超熵He）反映定性概念整体上的定量特征，将模糊性和随机性进行关联，构成定性和定量的映射关系。期望Ex代表定性概念的点，反映定性概念云滴群的重心位置;熵En用来衡量定性概念的模糊度与概率，反映定性概念的不确定性;超熵He即熵的熵，反映数域空间中代表该语言值所有点不确定度的凝聚性。

2.云发生器

云模型是通过云发生器实现定性概念和定量描述间的转换。正向云发生器实现定性概念到定量描述的转换，逆向云发生器完成定量描述到定性概念的映射。实现过程为：

输入：数字特征（期望Ex，熵En，超熵He），生成云滴数量n;

输出：n个云滴及隶属度u（x）。操作流程为：

（1）生成均值為En和方差为He的正态随机数si～N（En，He），i=1，2，…，n;

（2）生成均值为Ex和方差为si的正态随机数xi～N（Ex，si），i=1，2，…，n;

（3）计算隶属度ui（x）=，得ui（x）的云滴drop（xi，ui（x）） ，i=1，2，…，n;

（4）重复（1）到（3）的操作，直至生成n个云滴。

（三） 基于层次分析-云模型的数学核心素养对学生综合能力培养的效果分析

以高校A为例，结合校情、师情和学情，按照综合能力培养评估体系，考虑数学核心素养对学生综合能力培养的作用，结合专家指导，采用“优”“良”“好”“一般”“差”五级评价标准，运用层次分析法建立比较矩阵，获得综合能力培养评估各级指标因素的权重。

（1）综合能力培养评估体系的一级指标因素含有分析概括能力（权重45%）、批判创造能力（权重35%）和综合实践能力（权重20%）。

（2）分析概括能力的二级指标因素有理解知识能力（权重30%）、分析问题能力（权重25%）、文字表述能力（权重20%）和全局概括能力（权重25%）。

（3）批判创造能力的二级指标因素有质疑权威能力（权重20%）、发现问题能力（权重25%）、发散思维能力（权重30%）和解决问题能力（权重25%）。

（4）综合实践能力的二级指标因素有沟通协调能力（权重35%）、融会贯通能力（权重20%）、团队协作能力（权重30%）和灵活运用能力（权重15%）。

评语集是“好”“中”“差”之类的模糊概念，可采用一维正态云来描述每个评语。评语集是专家进行科学评判的依据和规范。一般而言，评语集中的评语数量是奇数。本文采用“优”“良”“好”“一般”“差”的五级定性语言，对应的评分区间为[80，100]、[70，80]、[60，70]、[50，60]、[0，50]。

由于本评价问题是多层次的综合评价问题，依据多层次评价的基本步骤，由最低层依次向高层次进行综合。以实际调查得到的学生自评结果作为数据来源，利用逆向云发生器先对每个二级指标的评分数据进行处理，每一个语言值型的指标对应一个云模型进行转换，获得每个二级指标的数字特征参数，如表2所示。

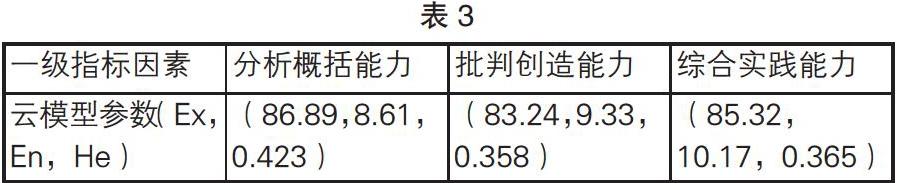
虚拟云是按照某种应用目的，对各基云数字特征参数进行计算，将结果作为新的数字特征构造成一个新云。运用虚拟云公式，将三个一级指标的子指标项的评价云综合起来得到每个一级指标的云模型的数字特征参数，如表3所示。

將一级指标的评价云综合起来得到最后的整体评价结果，评价云的三个特征值分别为：Ex=85.30，En=9.95，He=0.391。由此可见，综合评价结果的期望值为85.30，在区间[80，100]内。结果表明数学核心素养对学生综合能力培养可以起到有效的推动作用。

参考文献：

[1]李德毅，杜 鹢.不确定性人工智能[M].北京：国防工业出版社，2014.

[2]龚 杰，雍歧东，于 力，等.基于云模型和层次分析法的油料保障能力评估[J].兵工自动化，2018，37（1）：66-69.