航天器自适应有限时间反步控制
(浙江工业大学 信息工程学院,浙江 杭州 310023)
在编队飞行、卫星通信和太空站对接等诸多航天任务中,航天器姿态跟踪控制是任务成功的关键因素。航天器在轨运行时,往往存在着内部转动惯量不确定以及外部未知扰动等不确定因素的影响,为保证航天器的姿态跟踪性能,提出了许多非线性控制方法,包括滑模控制[1]、自适应控制[2]、反步控制[3]、逆最优控制[4]和H∞控制[5]等。其中,反步控制方法[6-7]是一种基于Lyapunov定理的递归设计方法,易于控制器设计,因此在航天器领域被广泛应用[8-9]。然而,传统反步法需要不断对虚拟控制律求导而导致复杂性爆炸问题,针对这一问题有研究者提出动态面方法[10],然而该方法并未考虑虚拟控制律通过滤波器以后产生的误差补偿问题。近来,Farrell等[11]提出一种命令滤波方法,在解决复杂性爆炸问题的同时,设计误差补偿信号弥补动态面方法的不足。然而,该方法设计的控制器只能保证系统状态在无穷时间内达到渐进稳定。与渐近稳定控制相比,有限时间控制能够保证系统状态的有限时间稳定,具有较快的收敛速度、较高的控制精度和较好的鲁棒性等特性,因此已被广泛应用于航天器控制中[12-14]。王辉等[15]结合反步法和滑模控制设计有限时间控制器,然而由于虚拟控制律指数项的作用,其导数可能会引起奇异值问题。马广富等[16]针对组合体航天器的姿态控制问题,提出基于命令滤波的有限时间控制方法,但其滤波器本身并不能保证有限时间收敛。Yu等[17]提出一种有限时间命令滤波反步控制方法实现系统状态的有限时间控制,然而其系统模型需要完全已知。
笔者针对惯量矩阵不确定和外部干扰的航天器姿态跟踪问题,建立基于四元数描述的系统模型;设计有限时间滤波器逼近虚拟控制律的导数,从而避免可能出现的奇异值问题;设计神经网络用于估计系统的不确定函数,并结合命令滤波反步法设计有限时间姿态跟踪控制器,从而保证系统的跟踪误差能在有限时间内收敛到零点附近;最后,给出数值仿真验证笔者所提方法的有效性。
1 问题描述
考虑由四元数描述的航天器运动学和动力学方程[18],即
(1)
(2)
(3)
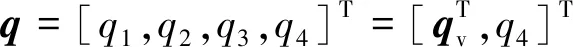
(4)
期望的姿态运动方程可以描述[19]为
(5)
(6)

考虑由四元数描述的航天器相对运动姿态,即
(7)
(8)
ωe=ω-Cωd
(9)

(10)
(11)
(12)
令J=J0+ΔJ,J0为转动惯量的已知标称值,ΔJ为转动惯量有界的不确定部分。将J=J0+ΔJ代入式(12)可得
(13)
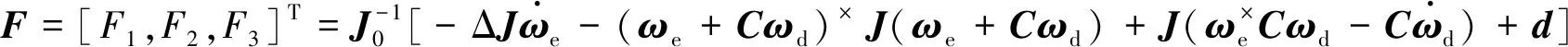
根据式(10)和式(13),姿态跟踪误差模型可以重写为
(14)
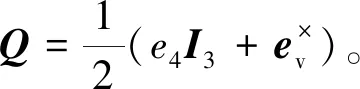
本研究的控制目标针对带有惯量矩阵不确定和外部干扰的航天器系统式(10~12),设计有限时间控制器,使得跟踪误差ev和ωe可以在有限时间内收敛到零点附近的小邻域内。
2 有限时间反步控制设计
2.1 有限时间命令滤波器
有限时间命令滤波器定义[20]为
(15)
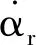
引理1[20]在输入没有噪声的情况下,等式在有限时间内成立,即
(16)
当输入受噪声影响时,假设输入噪声满足|αr-αr0|≤κ,其中αr0为实际信号,则在有限时间内,不等式成立,即
|φ1-αr0|≤ζ1κ=ϖ1
(17)
(18)
式中ζ1,ζ2为两个正常数。
2.2 神经网络
针对非线性系统中的未知函数f(Z),可设计神经网络进行估计,即
fnn(Z)=WTΦ(Z)
(19)
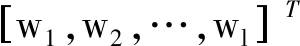
(20)
引理2[21]如果有在紧集Ωz上连续的函数f(Z),对于任何给定的精确度标准ε>0,则存在神经网络W*TΦ(Z),当节点数l足够多时有
f(Z)=W*TΦ(Z)+ε
(21)
式中W*为理想权值矢量,具体定义为
(22)
2.3 控制器设计
定义虚拟状态量
(23)
式中ωc为以下有限时间命令滤波器输出,即
(24)
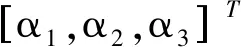
定义滤波误差补偿信号为ξ1和ξ2,然后令s1=z1-ξ1,s2=z2-ξ2。
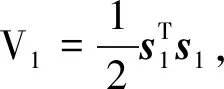
(25)
设计虚拟控制函数α和补偿信号ξ1为
α=Q-1[-k1z1-λ1sigγ(s1)]
(26)
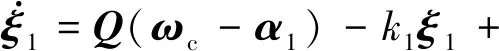
(27)
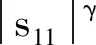

(28)

(29)
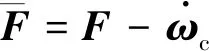
(30)
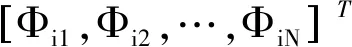
设计控制函数u和补偿信号ξ2为
(31)
(32)
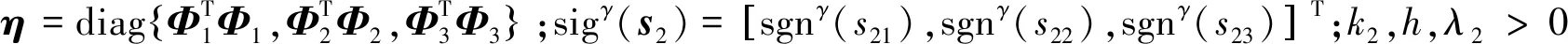
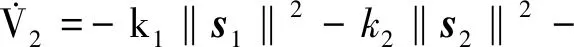
(33)
根据杨氏不等式,不等式成立,即
(34)
(35)
(36)
将式(34~36)代入式(33),可得
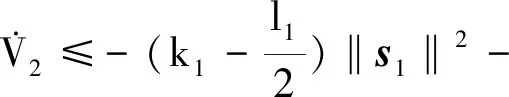

步骤3选取Lyapunov函数
(38)
并对其求导可得
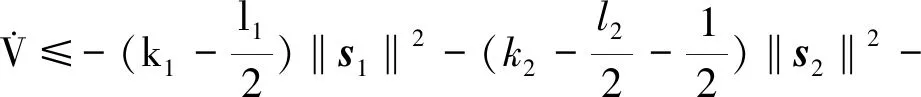
(39)
设计自适应更新律为
(40)
式中τ,m>0为设计参数。
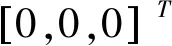
3 稳定性证明
在稳定性证明之前,首先给出有限时间引理。
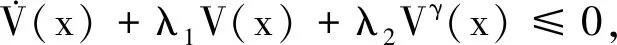
(41)
式中V(0)是V(x)的初始值。
定理1针对航天器系统式(10~12),设计限时间命令滤波器式(24),虚拟控制律式(26),实际控制律式(31),补偿函数式(27)、式(32)和自适应更新律式(40),则航天器姿态跟踪误差能够在有限时间内收敛到零点附近的小邻域内。
证明将自适应更新律式(40)代入式(39),可得
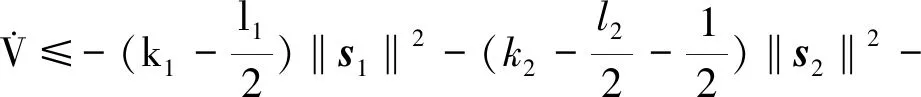
(42)
由杨氏不等式可知
(43)
由于0<γ<1,可得
(44)
将式(43,44)代入式(42),可得
(45)
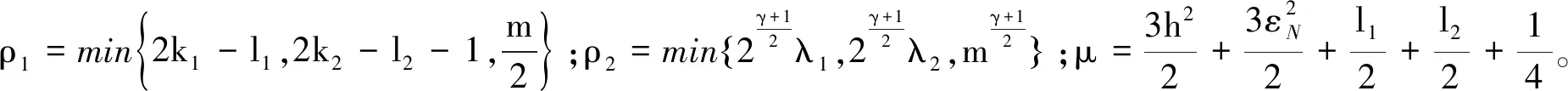
由于s1=z1-ξ1和s2=z2-ξ2,若能保证ξ1和ξ2在有限时间内收敛,则虚拟状态量z1和z2将在有限时间收敛到零点附近的邻域内。
因此,设计Lyapunov函数为
(46)
对式(46)求导,可得
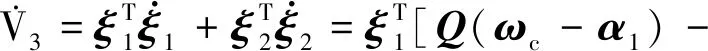
(47)
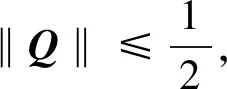
(48)
将式(48)代入式(47),可得
(49)
根据式(49)和引理3可得,选取适当参数l1,l2,ξ1和ξ2将在有限时间T3收敛到零点。因此,虚拟变量z1和z2可以在有限时间T=T1+T2+T3收敛到零点附近邻域内。根据定义式(23)可知,航天器状态能够在有限时间内跟踪期望轨迹。证毕。
4 数值仿真

ΔJ=diag{sin(0.1t),2sin(0.2t),
3sin(0.3t)} kg·m2
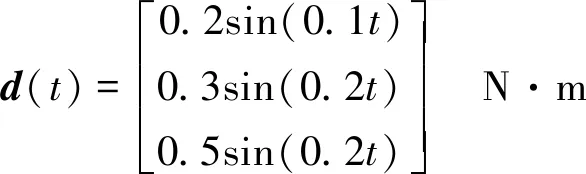
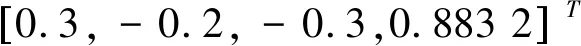
为了体现笔者提出控制方法的优越性,将对两种控制方法进行对比仿真:
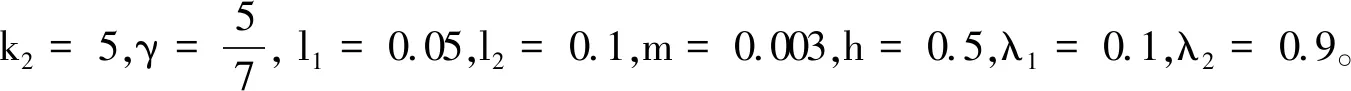
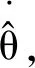
ωc=-k1Q-1z1
(50)
(51)
(52)
控制器相关参数选取均与M1方法相同。
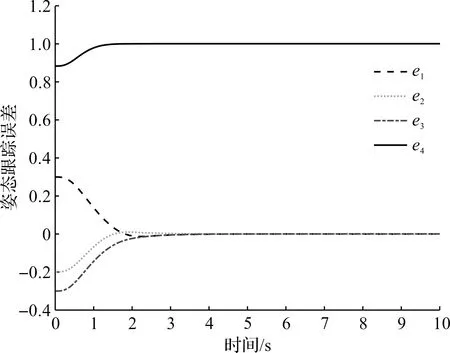
图1 M1四元数跟踪误差eFig.1 M1 quaternion tracking errors e
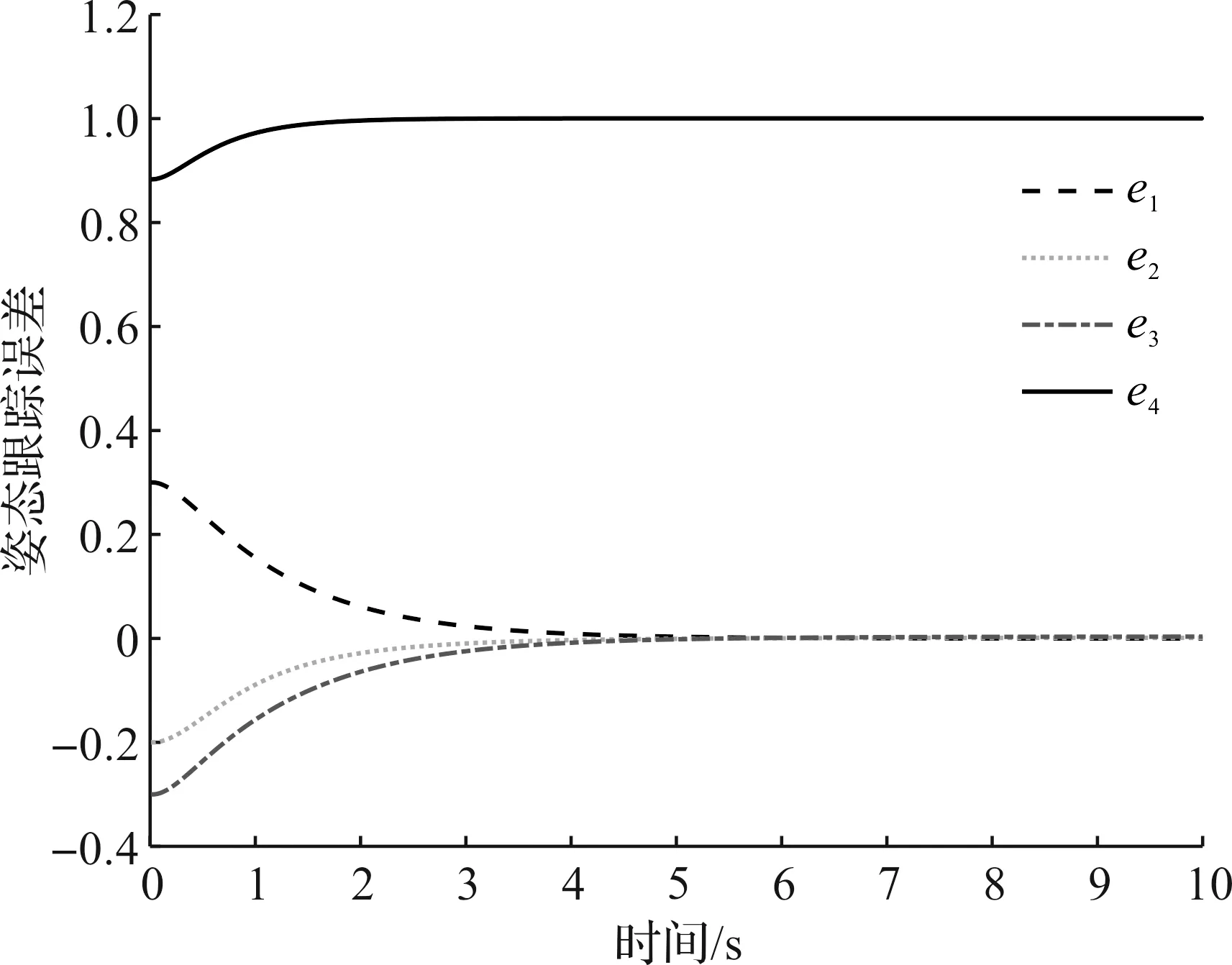
图2 M2四元数跟踪误差eFig.2 M2 quaternion tracking errors e
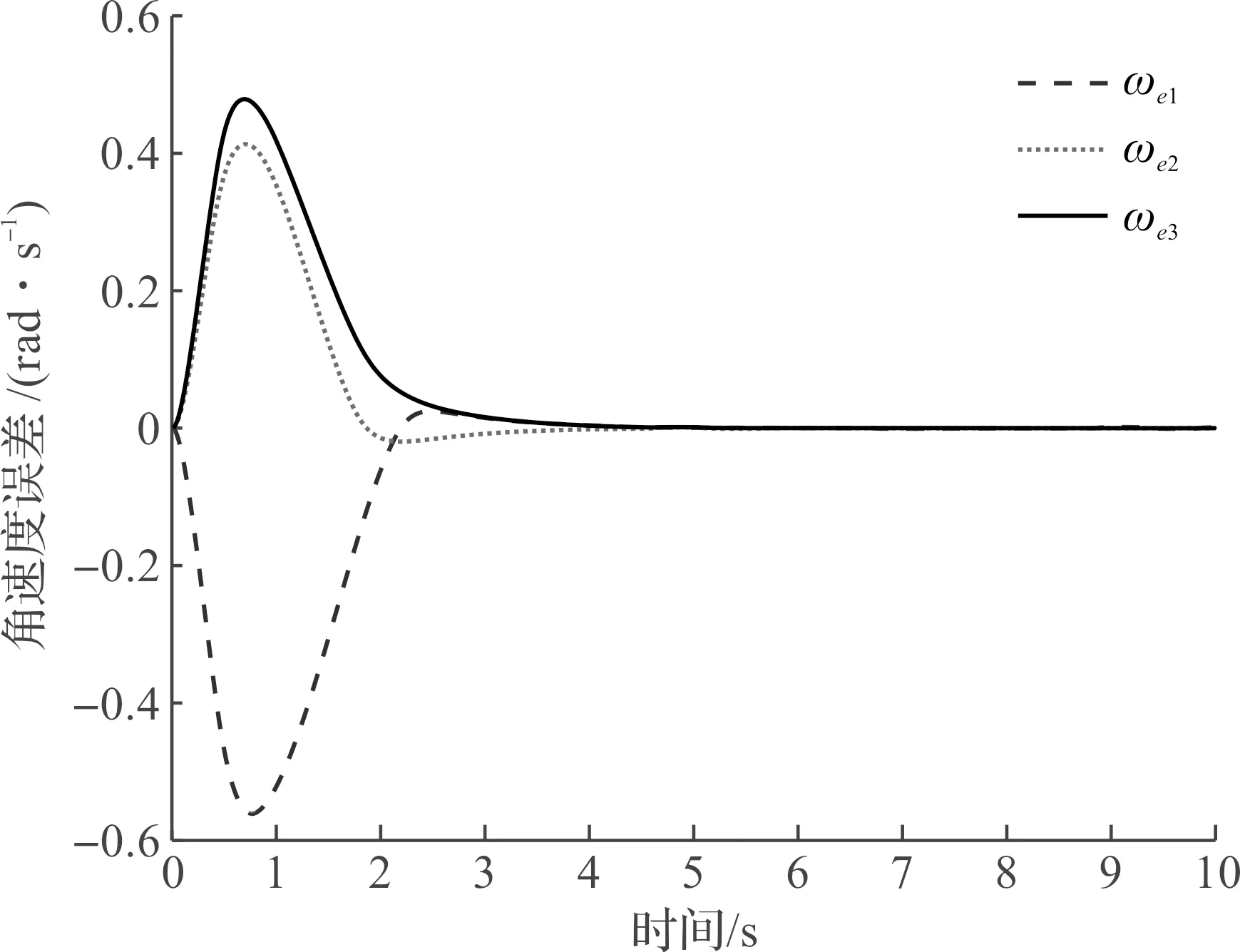
图3 M1角速度跟踪误差ωeFig.3 M1 angular velocity tracking errors ωe
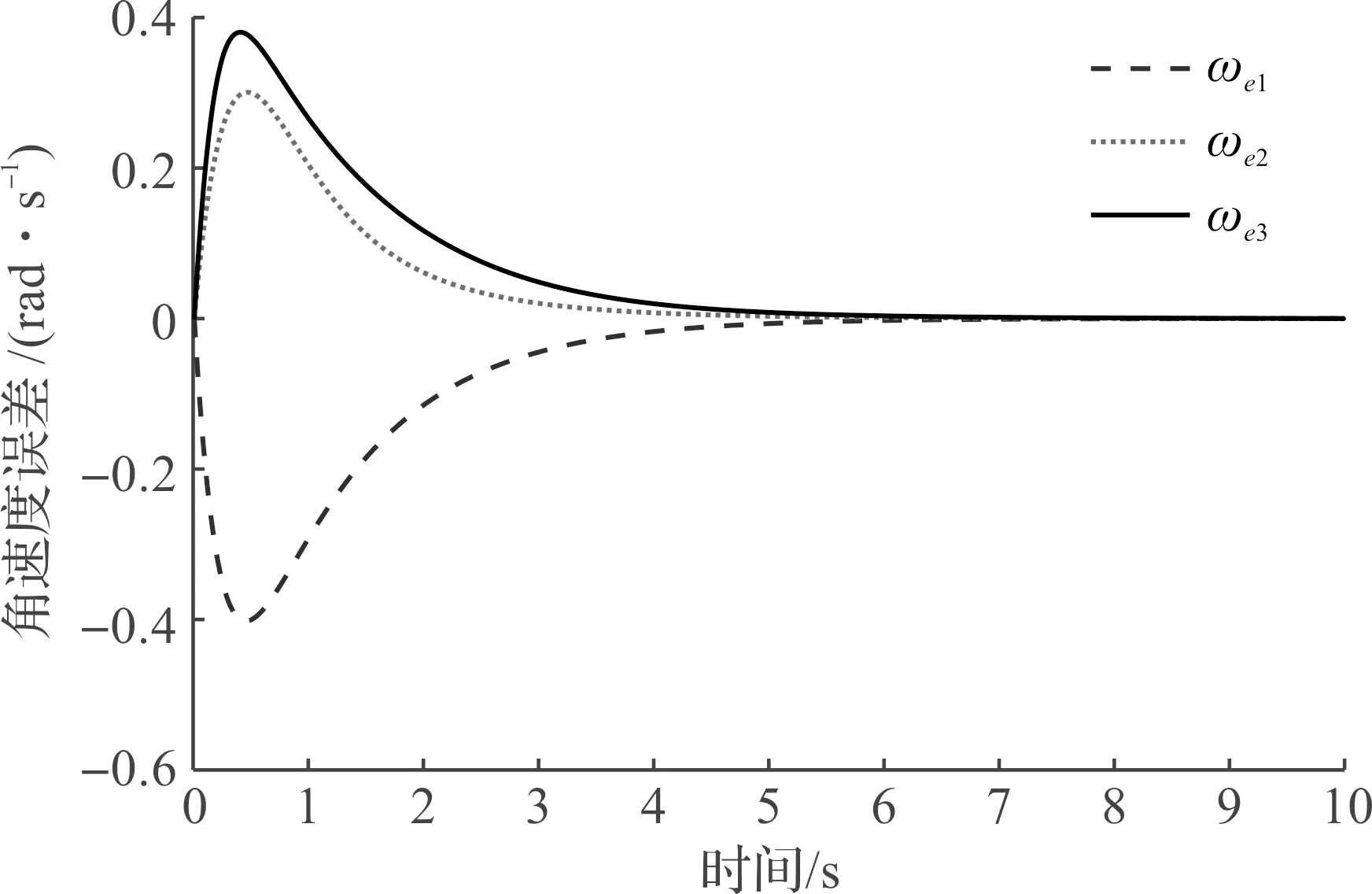
图4 M2角速度跟踪误差ωeFig.4 M2 angular velocity tracking errors ωe
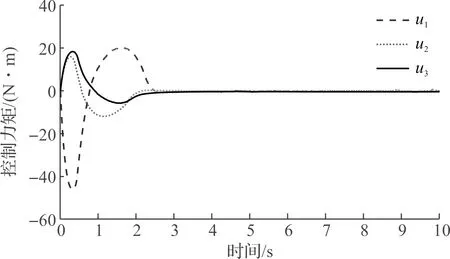
图5 M1控制力矩uFig.5 M1 control torque u
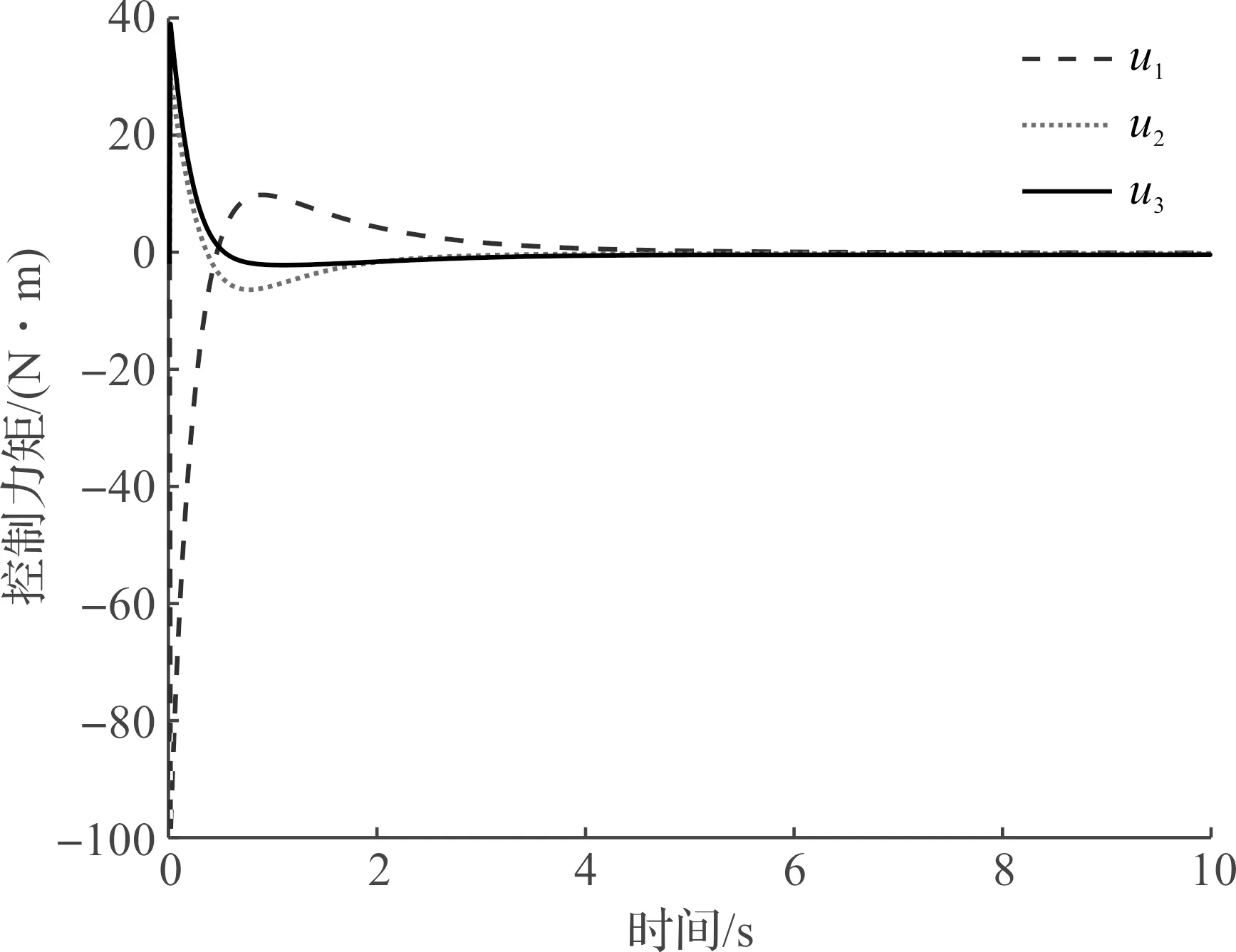
图6 M2控制力矩uFig.6 M2 control torque u
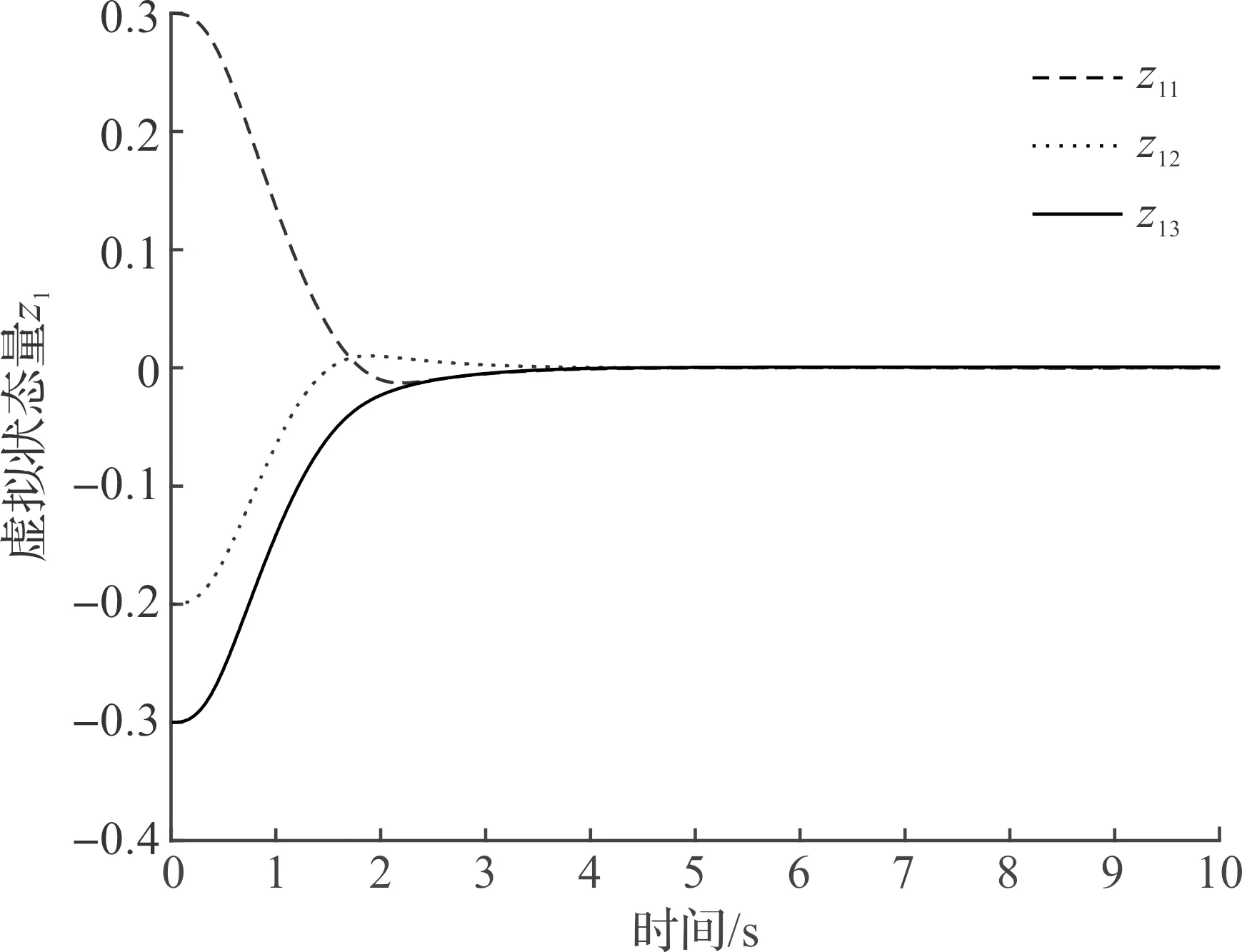
图7 M1虚拟状态量z1Fig.7 M1 virtual state z1
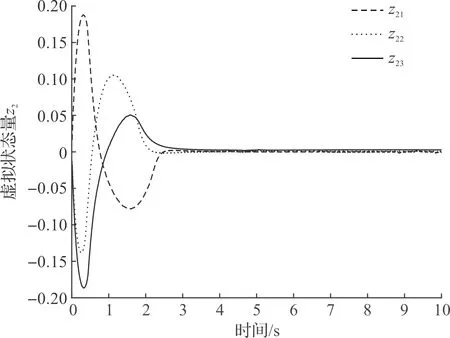
图8 M1虚拟状态量z2Fig.8 M1 virtual state z2

图9 M1估计参数Fig.9 M1 estimated parameter
5 结 论
针对带有转动惯量不确定和外部干扰的航天器,笔者建立基于四元数描述的姿态跟踪模型,并提出自适应有限时间反步控制方法。设计有限时间命令滤波估计虚拟控制律导数,进而避免奇异值问题。同时采用神经网络估计未知非线性函数,并通过给出稳定性分析,证明所设计控制器能够保证跟踪误差能够在有限时间内收敛。仿真结果验证了笔者方法的有效性。

