基于模糊理论和组合权重的光伏组件健康状况评估
贾玲,黄丽华,刘雪飞,韩璟琳,唐巍
(1. 河北农业大学 机电工程学院,河北 保定 071000;2.国网河北省电力有限公司 经济技术研究院,河北 石家庄 050021;3.中国农业大学 信息与电气工程学院,北京 100083)
光伏组件健康状况评估是光伏组件维修的依据,长期以来均通过定期检修、专家评定等判断光伏组件的健康水平和运行状况,以相关标准及运行经验为基准对光伏组件进行静态评估,通常用“正常、不正常”等来表述,无法准确描述具体的健康状况和状况的发展趋势.影响光伏组件健康状况的因素众多,且各因素影响程度各不相同,存在模糊性和不确定性,因此理论建模复杂.
目前常用的健康状况评估方法有人工神经网络、支持向量机和模糊综合评价法等.人工神经网络[1-2]是对人脑神经系统的模拟,具有联想记忆功能、自我调节和自我学习能力,但这种方法需要足够的学习样本来保证评估结果的可靠性;支持向量机[3-4]具有良好的拟合与泛化能力,能够映射高度非线性的输入与输出,但其二分类固有属性、核函数以及规则化参数选取困难使它在实际应用中存在一定的局限性.模糊综合评价法[5-6]是一种基于模糊理论的综合评价方法,首先将定性评价转换为定量评价,使用隶属度函数进行量化,然后根据多个影响因素进行综合性评判.该方法既考虑了评估对象的层次性,也可虑了影响因素的模糊性,使最终结果更加真实可靠.
文献[7]采用主成分分析法对原始多维输入变量进行预处理,利用马氏距离表征光伏系统的健康程度,但是存在结果过于依赖特征参数的选取,要与光伏系统性能对比,才能更好地评价光伏系统性能.文献[8]采用在线诊断方法对射频收发机进行研究,判断射频收发机的健康状况,对不良状况及时采取相应措施,使得射频收发机的寿命得以延长;文献[9-11]采用模糊理论和层次分析法对电力系统电压进行研究,得出其电压预警等级综合评估.文献[12]用层次分析法对指标体系进行分析,再利用神经网络实现电网的安全评估.文献[8-12]评估指标的权重仅仅通过主观赋权法(层次分析法)得到,人为因素影响较大,使得评估结果不能完全真实的反应事物本质.
鉴于以上分析,本文将主观和客观方法相结合,采用主观赋权法的层次分析法和客观赋权法的熵权法[13]相结合,确定光伏组件健康状况评估模型中的组合权重.依据模糊理论分析法对光伏组件健康状况做出综合评估.
1 评估指标体系的建立
对光伏组件健康状况评估需全面考虑各种影响其健康状况的因素,即光伏组件部件的所有参数.但是在实际工程应用中往往考虑主要因素忽略次要因素.为此,综合考虑影响因素所起作用的大小,选取重要影响因素作为反映光伏组件健康状况优劣的指标.若光伏组件的健康状况不佳,其输出功率、电流、电压等必然偏离其正常值;光伏组件还存在一些外在表象如断裂、黄变等现象,这些表象表明光伏组件已出现问题,会影响光电转换效率,使运行参数偏离正常值;光伏组件的工作环境也直接影响其运行参数,所以不能单纯依据运行参数的大小判断其健康状况,而是要将运行参数、外在表象以及工作环境参数紧密结合.为此本文的光伏组件健康状况评估指标体系包含3部分内容,即反映运行参数的运行指标、反映外在表象的巡视指标和反映工作环境参数的环境指标.运行指标、巡视指标和环境指标的因素多且各因素间相互影响,所以问题很复杂.为了便于分析,将复杂问题分解为多个简单问题逐一求解,将光伏组件健康评估指标体系分为3层,即目标层、准则层、指标层.目标层为上层,反映了光伏组件健康状况综合指标(A);准则层为中间层,包括运行指标(C1)、巡视指标(C2)、环境指标(C3);指标层为下层,反映健康状况的影响因素,包括太阳能直流功率(E1)、DC/DC光伏侧电压(E2)、DC/DC光伏侧电流(E3)、光伏组件温度(E4)、光伏组件效率(E5)、是否黄变(E6)、是否断裂(E7)、是否过温、过热(E8)、是否积灰(E9)、是否遮阴(E10)、总辐射(E11)、环境温度(E12)、相对空气湿度(E13)、风速(E14)、云量(E15).光伏组件健康状况评估指标体系如图 1 所示.

图1 光伏组件健康状况评估指标体系
2 多层次模糊理论综合评估模型的建立
模糊综合评判[14]侧重于评估对象的模糊性和不确定性,主要利用了模糊集合中隶属度和隶属函数,将定性评价转化为定量评价.影响光伏组件的健康因素很多且没有一个确定的等级划分,因此采用模糊评估法,根据模糊理论的原理,建立健康状况影响因素集、健康状况评估等级和隶属云[15-16],将层次分析法与熵权法相结合得到组合权重集,获得判断矩阵,从而进行模糊运算,得到更加合理的评判结果.
2.1 健康状况影响因素集
光伏组件健康状况评估指标体系中的指标层的影响因素构成了健康状况影响因素集,可用集合表示为
U={u1,u2,…,un},
其中,n是图1下层的健康状况影响因素的个数.
2.2 健康状况评估等级
本文采用相对劣化度[17, 18]反映设备(或系统)状态良好的程度,其数值介于[0,1]之间.根据指标性能的不同,分为越小越优、越大越优2种情况.健康状况评估等级用于评价光伏组件的健康状况,根据专家意见和运行经验,本文分为正常、注意、异常、故障4个等级,用集合表示为V={Ⅰ,Ⅱ,Ⅲ,Ⅳ}.越小越优运行状况与相对劣化度之间的对应关系如表1所示.越大越优运行状况与相对劣化度之间的对应关系如表2所示.

表1 越小越优健康状况与相对劣化度之间的对应关系Tab.1 The smaller the better the relationship between the health status and the relative deterioration

表2 越大越优健康状况与相对劣化度之间的对应关系Tab. 2 The greater the relationship between the better health status and the relative deterioration degree
2.3 隶属度模型的建立
隶属度[17-18]用来表示状况评估指标属于模糊集合的程度和等级,需要通过隶属函数来计算.隶属函数的建立需要依据影响因素的性质,本文的影响因素包括定量指标和定性指标,进而需要分别建立定量指标和定性指标的隶属度模型.
2.3.1 定量指标的隶属函数模型
传统的隶属函数选取依据性不强,从而导致计算结果的准确度不高.隶属云模型是在相对劣化度与健康等级相对应的基础上利用随机函数产生大量云滴形成的,更具有客观性,准确度更高.

(1)
(2)
Hei=q,
(3)
式中,i表示健康状况,分别取值为1、2、3、4;dmax、dmin分别表示相对劣化度的上、下限制;q的大小代表了模糊与随机的关联性,通常取0.01.
隶属云生成算法流程如下:



4)重复步骤(1)-(3),直到产生满意数量的云滴.
对应表1隶属云如图2所示.
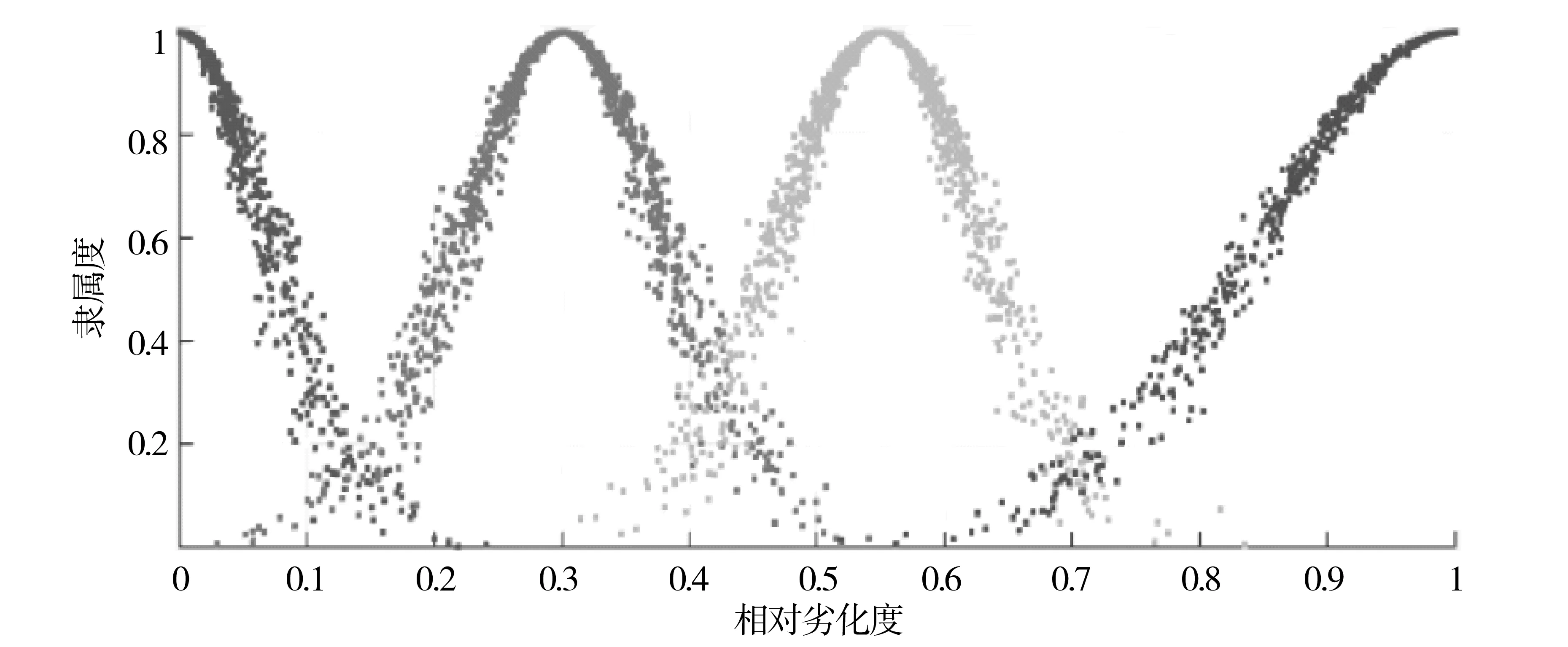
图2 隶属云
在图2的基础上,求解定量指标的隶属度,方法如下:
1)对定量指标进行归一化处理,得到相对劣化度g(x);
2)过g(x)=g0作一条平行于纵坐标轴的直线,与隶属云有N个交点,取N个交点对应的隶属度r的平均值作为该定量指标隶属于某状况等级的隶属度;
3)重复步骤2),得到各定量指标隶属于状况等级的隶属度.
2.3.2 定性指标的隶属函数模型
对于巡视因素等定性指标,本文采用模糊统计的方法,根据对多名领域专家的意见进行统计,得出各定性指标的隶属度,如式(4)所示.

.
(4)
2.4 组合权重模型的建立
本文将主客观权重分析方法综合考虑,形成了层次分析法[10]和熵权法相结合的综合分析法,规避了单一赋值法的缺点.
2.4.1 层次分析法权重模型
1)判断矩阵模型
标度是确定层次分析法权重的基础,本文的标度选取如表3所示,标度越大,代表影响程度越大.2、4、6、8分别表示为相邻标值的2个量之间的重要程度.同理,若相比较的2个量其中一个量的重要程度比另一个量低,根据低的程度,依次为1、1/2、1/3、1/4、1/5、1/6、1/7、1/8、1/9.从而分别求得环境指标、巡视指标、运行指标判断矩阵Cn×n。
(5)
其中矩阵中的元素Cij为第i个量对第j个量的重要程度.
2)特征向量模型
利用公式(6)求上述判断矩阵Cn×n的最大特征值λmax及其对应的特征向量v.
Cv=λmaxv.
(6)
3)权重模型
根据特征向量计算各因素的权重.
(7)
其中,vi为判断矩阵Cn×n的特征向量;∑vk为特征向量之和.
4)一致性检验模型
在计算每个因素的权重之后,需要进行一致性检验以验证权重的合理性.如果未通过一致性检验,则需要调整判断矩阵,直到满足一致性.可按照式(8)和(9)进行一致性检验.
CR=CI/RI
,
(8)
(9)
其中:CR为一致性比例;CI为衡量不一致程度的数量指标;n为判断矩阵阶数;RI为平均随机一致性指标.
当n≥3,且 0 对于表3中1-9阶判断矩阵,RI取值如表4所示. 表4 判断矩阵的平均随机一致性指标 2.4.2 熵权法权重模型 熵权法权重的求解过程如下: 1)对于n个数值型参数选取b组待评价对象,则得到评价矩阵 (10) 其中,qij为第j组对象在第i个指标的数值. 2)对数据进行标准化处理.由于各项指标的计量单位不统一,因此在计算综合指标前,先进行标准化和归一化处理,得到标准矩阵(θij)n×b. 3)计算第i项指标的熵值 (11) 4)计算第i项指标的熵权 (12) 2.4.3 组合权重模型的确定 建立了光伏组件健康诊断的指标体系后,运用AHP和熵权法分别计算出各个指标的权重,然后利用式(13)计算出指标的组合权重. (13) 式中:wi为层次分析法的权重;gi为熵权法的权重;Wi为 AHP—熵权法的组合权重. 光伏组件健康状况评估涉及因素繁多,状态参量数量很大,而且时时变化,想要建立一个精确的评估模型目前尚无可能,因此本文基于模糊理论建立了多层次模糊综合评估模型. 根据模糊理论分析搭建光伏组件健康状况评估模型, (14) 其中,W表示权重矩阵,R表示模糊关系矩阵,B表示评估等级的隶属度矩阵. 由于光伏组件健康状况评估指标体系具有多层次,因此模糊评估模型要运用在多个层次上,要对下层的影响因素集合求解对应的巡视指标、运行指标、环境指标的隶属度,该过程称为一级评估,再利用巡视指标、运行指标、环境指标的隶属度评估光伏组件最终的健康状况,该过程称为二级评估. 2.6.1 一级模糊评估的求解 1)定量指标的隶属度求解 将数值型影响因素进行归一化处理,采用云模型确定各状况量对各状况评级隶属度,形成模糊关系矩阵. 2)定性指标的隶属度求解 通过专家调查表确定各状态量对各状况评级的隶属度,形成模糊关系矩阵. 3)组合权重的求解 运用1~9标度法分别对运行指标、巡视指标、环境指标建立判断矩阵,利用式(7)计算各状况量的权重向量;针对指标层中各状况量数据,建立评价矩阵,利用式(12)计算各状态量的权重向量,最后利用式(13)计算组合权重向量. 4)一级模糊评判 2.6.2 二级模糊评估的求解 一级模糊评判结果即为运行指标、巡视指标、环境指标的隶属度.运用式(7)得到运行指标、巡视指标、环境指标的权重,运用式(14)得到模糊评判结果向量,依据最大隶属原则确定光伏组件的健康状况评估结果. 其程序流程如图3所示. 图3 程序流程 本文选取中国某地实际运行的光伏组件作为研究对象,原始数据如表5所示.利用Matlab编程,计算结果见表5. 表5 原始数据 1)运行指标、巡视指标、环境指标的隶属度矩阵分别为 2)运行指标、巡视指标和环境指标的权重分别为 3)一级模糊综合评估结果: ①运行指标的隶属度B1=[0.613 0.261 0.126 0]. ②巡视指标的隶属度B2=[0.915 0.085 0 0]. ③环境指标的隶属度B3=[0.558 0.442 0 0]. 5)二级模糊综合评估BA=[0.706 0.228 0.066 0]. 最终解得光伏组件综合模糊评估隶属度矩阵为[0.706 0.228 0.066 0],该结果表明光伏组件属于正常状况的隶属度为0.706、注意状况的隶属度为0.228、异常状况的隶属度为0.066、故障状况的隶属度为0.根据最大隶属度原则,该光伏组件等级为“正常状况”. 1)通过对光伏组件健康状况评估的研究,提出了光伏组件的健康状况评估方法,即基于模糊理论和组合权重的光伏组件健康状况评估方法.该方法涵盖了定量指标和定性指标的求解,因此也适合其他组件或设备的健康状况评估. 2)基于模糊理论,利用隶属云确定定量评估指标的隶属度,避免了利用传统隶属函数求解隶属度带来的主观性强的问题.将层次分析法和熵权法相结合得到组合权重,降低了权重的主观性,结果更加客观合理. 3)采用Matlab编程,对某地区的光伏组件进行了健康状况评估,结果表明该方法是可行的、有效的.
2.5 多层次模糊综合评估模型

2.6 基于光伏组件健康状况综合评估的求解

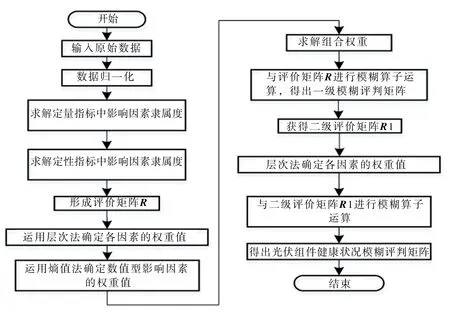
3 实例分析

4 结论

