细管实验确定最小混相驱压力技术标准

杨付林，喻 鹏

(1.北部湾大学，广西 钦州 535011； 2.广西高校北部湾石油天然气资源有效利用重点实验室，广西 钦州 535011)

0 引 言

MMP下注入气体是提高原油采收率普遍和实际的方式之一[1-2]。MMP是在一定油藏温度下，注入气体与原油经过多次接触达到混相的最小压力[3]。油藏原油的混相较强地依赖注入气体的压力，如果注入气体的压力低于MMP，气体驱替原油不能完全达到混相，进而降低ORF。在较高注入压力下，气体与原油易发生混相，但过高的注入压力使项目运行的成本大幅度增加，同时也增加了项目的安全风险，因此，准确地确定MMP十分必要。确定MMP方法主要包括实验法、经验公式法和数值计算法[4-6]。在这3种类型方法中，实验法是最准确和可信的。常用的实验法主要包括细管实验法[7]、升泡仪法[8]和消除界面张力法[9]。细管实验法是被广泛使用并为石油领域认可的确定MMP的标准方法。截至目前，暂无被普遍认可和使用的规范实验设计、流程和确定MMP的技术标准。

基于细管实验测定的ORF与注入压力关系曲线，文献中已介绍和描述了一些确定MMP的标准[10-11]。为了简化，在研究中称为ORF标准。在早期发表的文献中，在CO2突破后ORF大于80%或最终ORF为94%时，相应的注入压力即为MMP[12]。也有人将注入1.2倍孔隙体积气体后，ORF为90%或95%时的注入压力确定为MMP。普遍认可的是注入1.2倍孔隙体积气体后，ORF大于90%时的注入压力即为MMP，其也被用作动态的多次接触混相的指标[11]。Wu R S[11]等将混相和非混相驱的ORF与注入压力数据进行线性拟合，用其相交点来确定MMP。如果线性相交或转折变化不够剧烈，需要采用转折压力标准来确定MMP。当单位压力的ORF增加值等于一个任选的低阈值斜率时，对应的压力即为MMP[13]。可见，对于确定MMP的技术标准没有一个普遍的共识，如阈值或数值选项的详细描述[14]。截至目前，几乎没有报道关于确定MMP技术标准的系统研究和量化对比。为了准确确定MMP，先通过细管实验，得到油样的ORF与注入压力的关系曲线，再依据ORF标准和BOP标准进行系统研究和定量对比，从而确定MMP。在ORF标准中，采用了线性外推和线性相交方法，在BOP标准中采用了3次方拟合方法。

1 细管实验测定MMP

1.1 实验样品

原油样品取自江苏油田L6区块(50 ℃地面脱气原油黏度为12.3 mPa·s)，正戊烷(n-C5H12)和正十六烷(n-C16H34)，试剂级，国药集团化学试剂公司。模拟油的组成为物质的量的比为0.43∶0.57的n-C5H12/n-C16H34混合物。CO2的纯度为99.5%，在使用时，没有进一步纯化或调整。

1.2 细管实验及方法

实验细管的特征见表1。

实验方法：在温度为100 ℃条件下，用已蒸馏处理的丙酮清洗细管并通N2吹干；细管加热至设定的温度(油藏温度)，在设定的压力下，用泵注入油样并饱和细管；在设定的温度和压力下，驱替泵注入速度为12.0 cm3/h，将CO2注入细管中驱替油；在细管实验中，记录注入气体的孔隙体积倍数及产出油的体积，每10 min采集一次数据；注入1.2倍孔隙体积气体后，结束实验。实验测定了2组油样的MMP：模拟油和江苏油田L6区块原油。对于每组体系，细管实验在5个不同压力下运行。对于L6区块原油，测试的温度为60 ℃。为与文献中MMP对比，模拟油体系测试的温度为40 ℃。

表1 细管的特征

2 实验结果及讨论

图1为60 ℃不同注入压力(pinj)下ORF与注入CO2孔隙体积倍数的关系曲线。

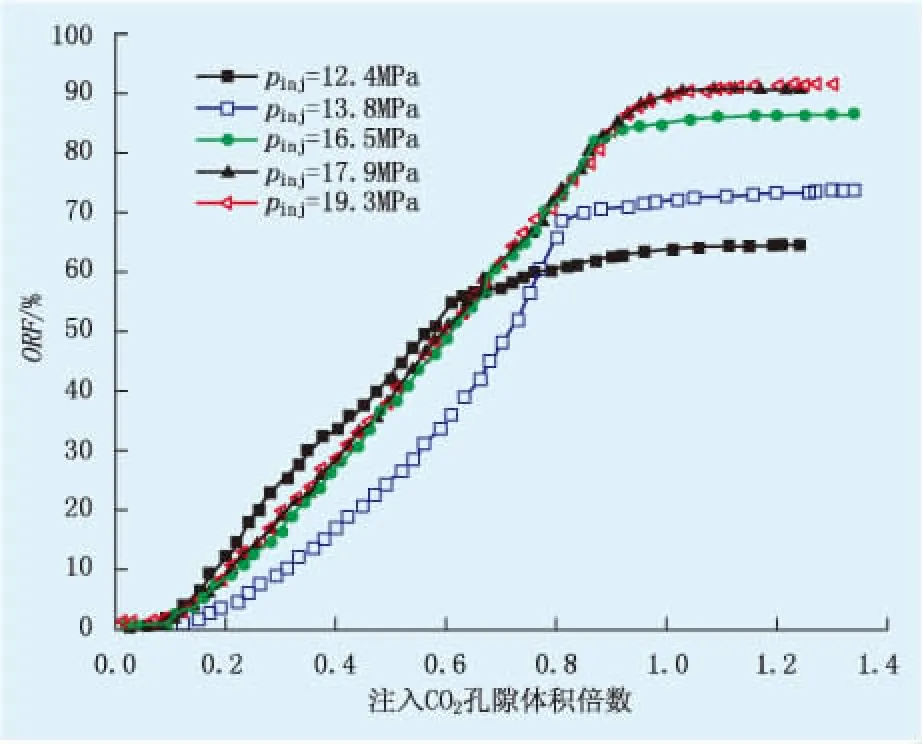
图1 不同pinj下注入CO2孔隙体积倍数与ORF关系

由图1可知：随着注入CO2孔隙体积倍数增加，ORF增加，在注入1.2倍孔隙体积后，达到最大值；在注入CO2初期，pinj=12.4 MPa的ORF比pinj≥13.8 MPa的ORF大，这是因为低注入压力下CO2的溶解度较低，大部分注入的CO2通过细管驱替原油，仅少部分的CO2溶入原油；当pinj≥16.5 MPa时，初始阶段ORF较低，随着注入CO2孔隙体积倍数的增加，ORF持续增加，在注入CO2为1.2倍孔隙体积时，达到最大值；在注入1.2倍孔隙体积CO2时，ORF随压力的增加，增加幅度减小。因此，可推断注入的CO2与原油在pinj≥17.9 MPa为混相，pinj=16.5 MPa为近混相，pinj≤13.8 MPa为非混相。

2.1 ORF标准

图2为ORF标准采用线性外推法确定MMP。线性外推法是将非混相和近混相的细管实验数据点线性拟合为一条直线，根据ORF阈值外推出MMP。通过线性拟合4个细管实验数据点，MMP等于ORF阈值为90%和95%的横坐标值(注入压力)，相应的MMP分别为17.5、18.6 MPa。因此，在无明确的ORF阈值情况下，给出较小的MMP范围优于单一的MMP值。

图2ORF标准采用线性外推法确定MMP

图3描述了依据ORF标准采用线性相交法确定的2个MMP。在该方法中，有2个数值选择：第1个数值选择为找到前4个数据点的线性拟合与后2个数据点的线性拟合的交点，在该方法中，第4个数据点作为共同点被使用了2次；第2个数值选择是找到前4个数据点的线性拟合与第5个数据点的线性拟合的交点，原理上，线性相交的方法确定MMP是通过找到ORF与注入压力关系曲线上斜率的突变点。关系曲线分为2个明显的压力区，即非混相区和混相区。基于5个细管实验的ORF与注入压力数据，获得的3条直线(Ⅰ、Ⅱ和Ⅲ)代表了前4个、后2个和第5个数据点的线性拟合。LineⅠ与LineⅡ和LineⅠ与LineⅢ的交点见图3。对应的横坐标即为2个MMP。因此，依据ORF标准采用线性相交法确定2个MMP分别为17.6 MPa和17.9 MPa。

图3ORF标准采用线性相交法确定MMP(2个数值选择)

2.2 BOP标准

若测定的ORF与注入压力关系曲线的斜率或转折点变化不大，用上述ORF标准的线性相交法确定的MMP不是很精确[10]，为此，采用BOP标准确定MMP。根据BOP标准，当单位压力的ORF增加值等于一个任选的低阈值斜率时，对应的注入压力即为MMP。对5个细管实验数据点，进行3次方拟合，3次方程为：

ORF=46.65926+8.45062pinj+0.23247pinj2-0.01549pinj3

(1)

对式(1)求导，得：

ORF=8.45062+0.46494pinj-0.04647pinj2

(2)

式(2)可用来确定在任一压力下，单位压力的ORF增加值。根据BOP标准，选择不同的阈值斜率，确定相应的MMP。实验中1%、2%、3%MPa-1的阈值斜率分别对应的MMP为18.6、17.8、16.9 MPa。

2.3 2个标准的对比

表2为依据ORF标准、BOP标准确定的MMP和范围的对比结果。

由表2可知，对于同一条ORF与注入压力的关系曲线，如果采用不同标准和不同的拟合方法来确定MMP，可获得不同的MMP范围。因此，依据任何一种标准确定MMP，以较小的压力范围方式表达MMP，该表达方式优于给出唯一的明确MMP值的方式。同时发现采用不同标准对于一个给定的原油体系，存在一个较小的共同MMP范围。

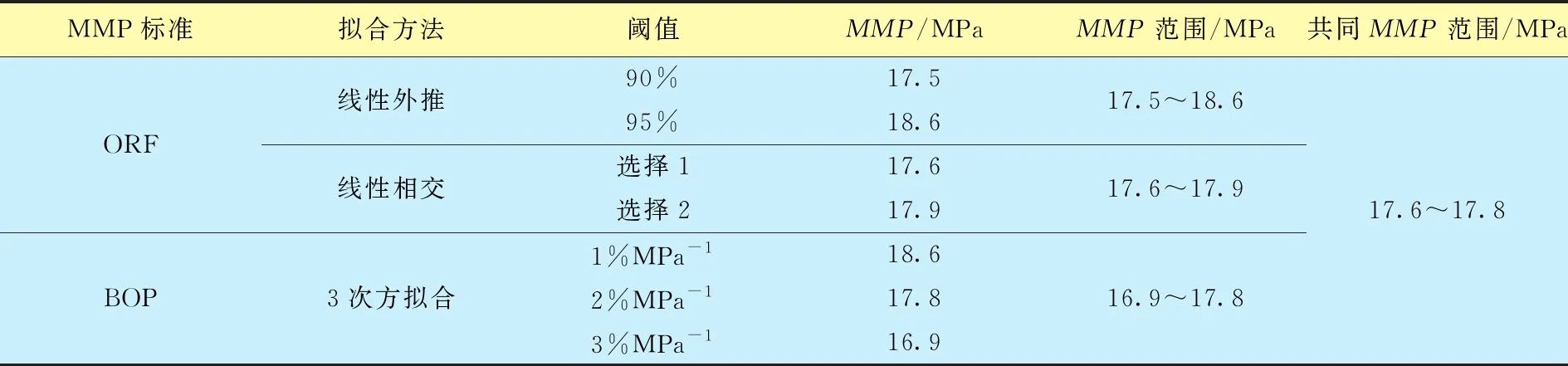
表2 ORF标准、BOP标准确定MMP和范围的对比

由表2可知：依据ORF标准，ORF阈值(90%～95%)越高，确定的MMP越大。线性相交方法对于测得的ORF与注入压力数据的分布较为敏感；线性相交方法给出一个相对较小的MMP范围。因此，线性外推方法确定的MMP精度高于线性相交法。该认识与文献[10]观点相一致，Wu R S等人[11]认为，线性相交法无论哪种数值选项，确定的MMP精度较低。BOP标准是基于5个细管实验点的3次方拟合，通常认为3次方拟合法较好地描述了数据点的变化趋势。与采用ORF标准的线性外推法对比，BOP标准确定MMP对选择的低阈值尤其敏感。另外，采用BOP标准的3次方拟合法确定的MMP是一个较大的压力范围。若想获得较精确的MMP，应选择1%～2%MPa-1低阈值斜率。

2.4 模拟油的MMP与文献结果对比

为与文献[11]中MMP对比，选择相同的模拟油进行细管实验，测试的温度为40 ℃。实验测得的ORF与注入压力关系曲线斜率变化较大，依据ORF标准，采用较精确的线性拟合法确定MMP。图4描述了ORF标准采用线性拟合法确定的MMP。ORF阈值为90%和95%，相应的MMP分别为10.1、10.7 MPa，与文献[11]中ORF为95%的MMP基本吻合(10.3 MPa)。这证明了细管实验数据是可信的，以较小的压力范围(10.1～10.7 MPa)方式表达了MMP，该表达方式优于给出唯一的明确MMP值的方式。

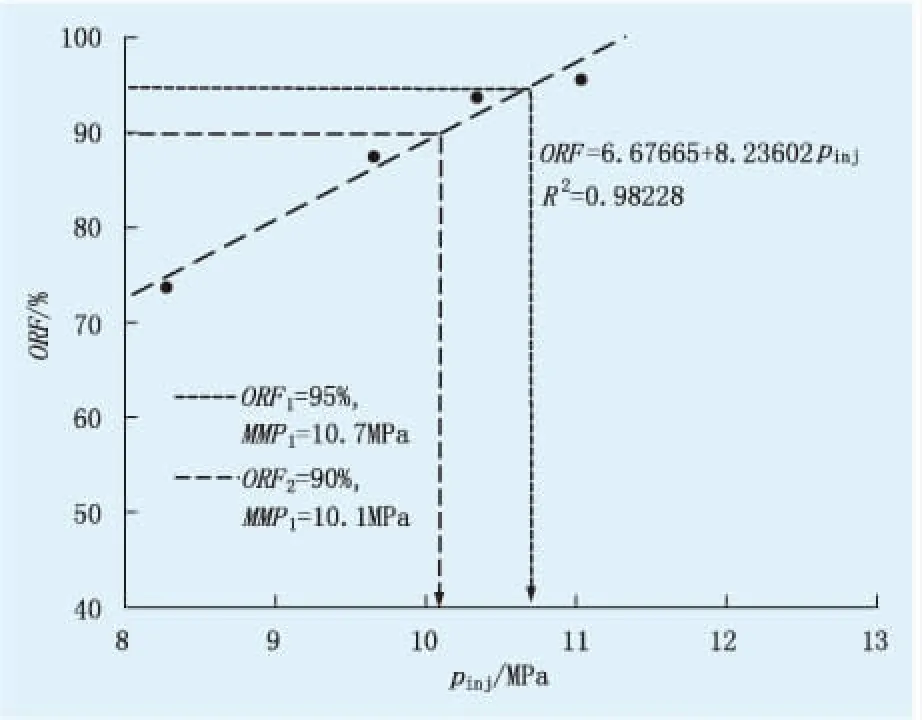
图4 模拟油采用线性拟合法确定MMP

3 结论及建议

(1) 线性相交方法对于测得的ORF与注入压力数据的分布较为敏感。线性相交方法给出一个相对较小的MMP范围，与线性外推法对比，线性相交法确定的MMP精度较低。

(2) 在近混相条件下，确定测定的ORF与注入压力的数据是十分重要的。依据ORF标准确定MMP时，为了获得较精确的MMP，近混相条件下的数据应包括在线性拟合的注入压力范围中。

(3) BOP标准的3次方拟合法对低阈值斜率的选择很敏感。若选择1%～2% MPa-1低阈值斜率，可获得较精确的MMP。

(4) 使用同一组ORF与注入压力关系的细管实验数据，采用不同的标准和不同的拟合方法，可获得不同的MMP范围。因此，建议以较小的压力范围方式表达MMP，该表达方式优于给出唯一的明确MMP值的方式。