非均质致密储层微观力学特征分析及脆性评价方法研究

冯笑含，赵万春，王婷婷

(东北石油大学，黑龙江 大庆 163318)

0 引 言

目前，非常规油气资源的开采需通过大规模体积压裂方式制造压裂缝网对储层进行改造。在非均质储层压裂效果评价中，岩石脆性是天然裂缝生成及缝网形态的重要影响因素之一[1]。因此，在压裂方案中，需对储层进行脆性评价分析，判断缝网形态及连通范围[2]。目前，岩石脆性评价的方法多达数十种，各自具有其优势和局限性[3-13]，而现场普遍接受并采用主要是弹性参数法[14]及矿物成分分析法[15]。弹性参数法认为岩石弹性模量的升高及泊松比的降低均能增强岩石的脆性，岩石矿物成分分析法认为岩石中石英等矿物的含量越高，岩石脆性指数越大。Burnaman等[16-17]认为脆性矿物是导致压裂过程中产生不同缝网形态的重要原因，并优化了矿物成分分析方法。丁文龙等[18]认为石英、长石和碳酸盐岩含量增高均会使岩石脆性增大，储层易产生天然裂缝。现有的研究手段都是从岩心的整体失稳进行描述，在微观破裂领域无法进行有效分析，而矿物组分法等类似方法将岩石矿物定性为脆性、非脆性矿物，与实际情况有较大误差。因此，需要建立新的脆性评价方法，用以在微观领域进行研究。

1 岩体微观力学特征分析及脆性表征

1.1 逐步回归模型建立

采用逐步回归分析方法，对矿物成分进行筛选分析，确定重点影响岩石弹性模量及泊松比的参数。当被解释变量同时受多个因素影响时，利用求解求逆紧凑变换法和双向检验法，逐个分析解释变量对被解释变量的贡献程度，建立最优回归方程。该方法通过反复检验，可剔除具有多重共线性的解释变量，并逐步引入贡献最大的解释变量，使回归方程更全面和精准。模型包含的被解释变量为岩石的弹性模量和泊松比，解释变量为岩石矿物成分含量测定值，建立的回归模型为：

(1)

通过实验得到n组实验数据，根据实验数据计算解释变量与被解释变量间的相关系数。并根据不同变量间的相关系数建立回归分析初始相关系数矩阵：

(2)

式中：rij为变量i、j(同时包含解释变量与被解释变量)间的相关系数；R为初始相关系数矩阵。

根据初始相关系数矩阵，计算不同解释变量与被解释变量间的偏回归平方和，表征不同解释变量在回归方程中的贡献度：

(3)

式中：ui为回归变量贡献度。

选择最大偏回归平方和uimax对应的解释变量作为引入变量，经F检验法进行分析，当检验结果大于经验性确定的临界阈值，该变量可引入回归方程作为回归变量，反之，该变量无法引入回归方程，需要剔除。

引入成功后，需将所引用的解释变量作为主元素，通过求解求逆紧凑变换法剔除该变量产生的贡献度，计算新的相关系数矩阵，并通过新相关系数矩阵重新计算各解释变量偏回归平方和，求出剩余变量贡献度，从而通过F检验确定新引入的回归方程变量，直至回归方程无法引用与剔除任何变量，此时，所选中解释变量即为回归方程的引入自变量。

选定回归方程解释变量后，可通过式(4)计算各变量对应的回归系数，未被选中的变量的回归系数均为0，计算完成后将实验数据平均值代入回归方程计算回归系数。

(4)

式中：σi为解释变量i的实验数据方差；σY为被解释变量Y的实验数据方差；l为回归方程最终选择变量的数量。

将计算得到的回归系数带入逐步回归方程中，即可得到岩石弹性模量及泊松比的回归模型。通过该模型，可由岩石矿物成分计算得到不同区域内岩石的弹性模量及泊松比。

1.2 岩体微观脆性分布表征

在微观研究中，岩石整体可离散出无数微元体(图1)，不同微元体中岩石矿物含量具有差异性，根据离散后不同微元体矿物含量差异即可计算岩石局部脆性。

图1 岩心离散化示意图

此时，微元体方位可由(a，b，c)表征，根据矿物微区衍射实验测定该单元矿物成分，并通过回归方程计算该单元的弹性模量及泊松比，记为E(a，b，c)与v(a，b，c)。结合弹性参数法表征岩石脆性分布，可得离散化岩石脆性分布规律：

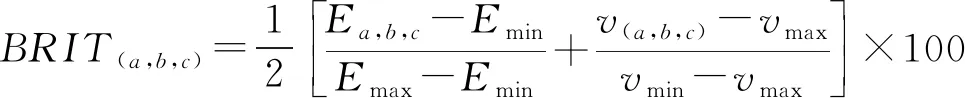
(5)

式中：BRIT(a，b，c)为岩石微元体(a，b，c)处的脆性；Emax为岩石弹性模量最大值，GPa；Emin为岩石弹性模量最小值，GPa；vmax为岩石泊松比最大值；vmin为岩石泊松比最小值。

该模型从微观层面建立了岩石脆性与岩石力学性质之间的联系，计算离散化岩石局部脆性分布规律，定量、精准地表征岩石矿物成分对微元体脆性的影响，精确判断岩石压裂过程中的受力薄弱点，确定岩石易产生微观破裂的方位，从而根据微裂缝萌生及扩展规律判断岩石失稳状态下的缝网连通扩展形态，为岩石从整体失稳研究过度到微观劣化研究提供了科学探索手段及研究基础。

2 力学参数回归分析与检验

实例岩心取自辽河油田A区块同一目的层，共计20块标准岩心。通过真三轴抗压实验测量岩心弹性模量及泊松比，并选取实验后的岩心碎块制成薄片，通过X射线衍射仪进行微区矿物成分衍射实验，测量不同岩心矿物组成成分(表1)。

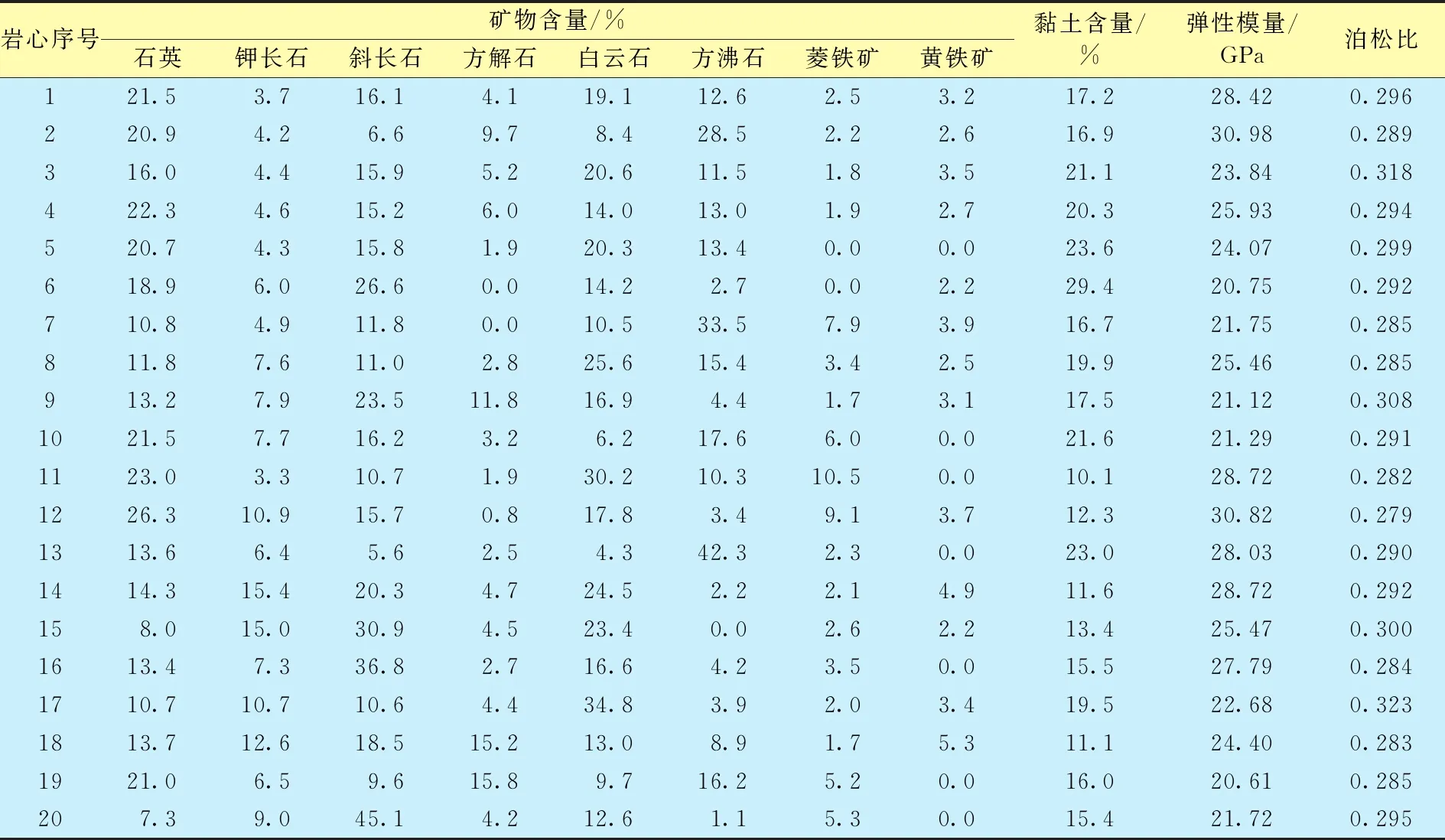
表1 岩心实验测定结果

由表1可知：岩心的弹性模量测量结果为20.61～30.98 GPa，泊松比测量结果为0.279～0.323；岩心主要由9种矿物成分构成，分别为石英、钾长石、斜长石、方解石、白云石、方沸石、菱铁矿、黄铁矿以及黏土矿物。将实验数据带入计算模型中，建立初始相关矩阵，岩心弹性模量及泊松比的解释变量经多次引入及剔除后，通过式(4)计算得到弹性模量及泊松比的回归系数(表2)。

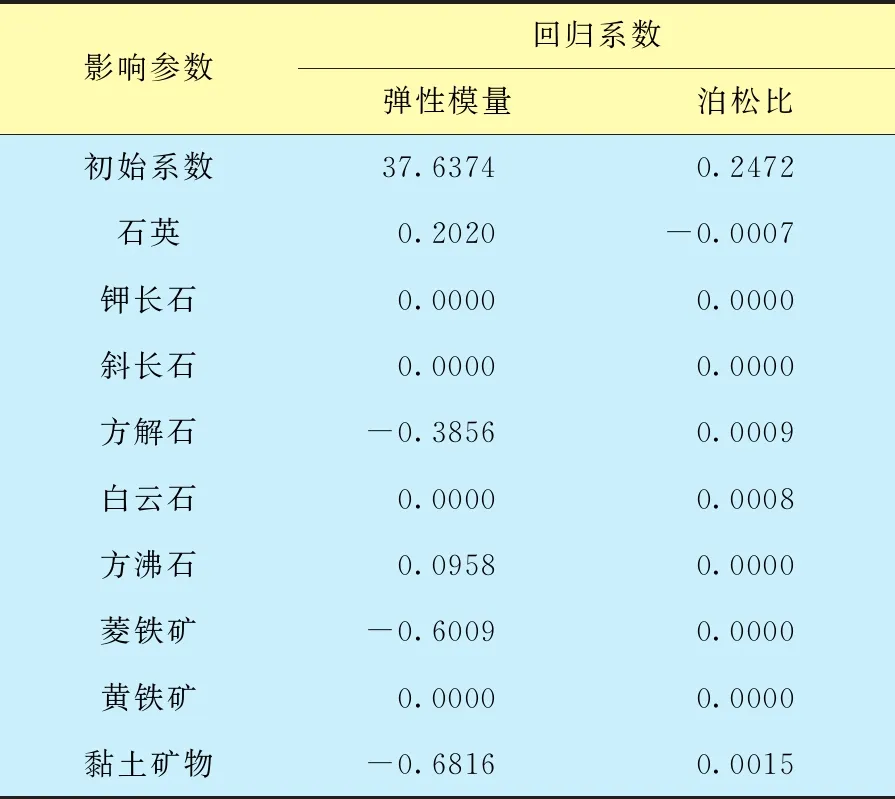
表2 回归系数计算结果

将逐步分析回归系数结果代入基础模型中，可以建立岩石矿物成分对力学性质影响的回归方程：

E=37.6374+0.2020x石英-0.3856x方解石+
0.0958x方沸石-0.6009x菱铁矿-0.6816x黏土

(6)

v=0.2472-0.0007x石英+0.0009x方解石+
0.0008x白云石+0.0015x黏土

(7)

分析式(6)、(7)可知：在模拟辽河油田地层实际储层参数情况下，剔除非显著性因素后，岩石弹性模量主控因素包括石英、方沸石、菱铁矿、方解石以及黏土含量，其数值随石英、方沸石的含量升高而增加，随菱铁矿、方解石以及黏土的含量升高而降低；岩石泊松比主控因素包括石英、白云石、方解石以及黏土含量，其数值随白云石、方解石以及黏土的含量升高而增加，随石英含量的升高而降低。

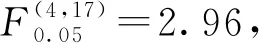
3 微观脆性评价方法适用性分析

对岩体微观力学性质与矿物成分间逐步回归模型进行显著性检验分析，结合弹性参数法，将式(6)、(7)带入式(5)，建立了新的岩体微观脆性评价方法：

(8)

式(8)为辽河油田A区块岩石微观脆性评价模型，该模型从微观矿物成分分析入手，建立了微观矿物成分与岩体脆性间的定量表征关系。通过该方法计算岩体脆性分布，忽略了岩体宏观力学特征分析，从微观层面表征储层压裂过程中易破裂区域，可为压裂选层提供精细量化技术指导。

将岩心实验测定结果带入新脆性评价模型，计算该层段岩石脆性分布状态，并与矿物成分分析法、弹性参数法计算结果及现场测定脆性对比分析(图2)。由图2可知：①岩心脆性的整体变化趋势是相同的；②岩石矿物成分分析法计算的脆性指数与现场实际情况相比严重偏低，主要原因是该方法仅对矿物成分进行了定性分析，因此，通过该结果对压裂后缝网形态判断会产生较大偏差；③弹性参数法计算的脆性指数与现场测定结果对比差值较大，存在一定的计算误差，主要原因是弹性参数法所需的输入参数——弹性模量是通过室内实验分析测定的，与现场声波测定结果存在明显差异；④新方法计算的脆性指数变化规律与现场测定结果误差最小，可有效代替弹性参数法进行脆性分析，且该方法结合矿物成分对储层脆性的影响，从微观层面研究储层脆性变化规律，能够更容易判断裂缝破裂区域，预测压裂缝网形态，为现场施工提供更科学有效的判别依据。

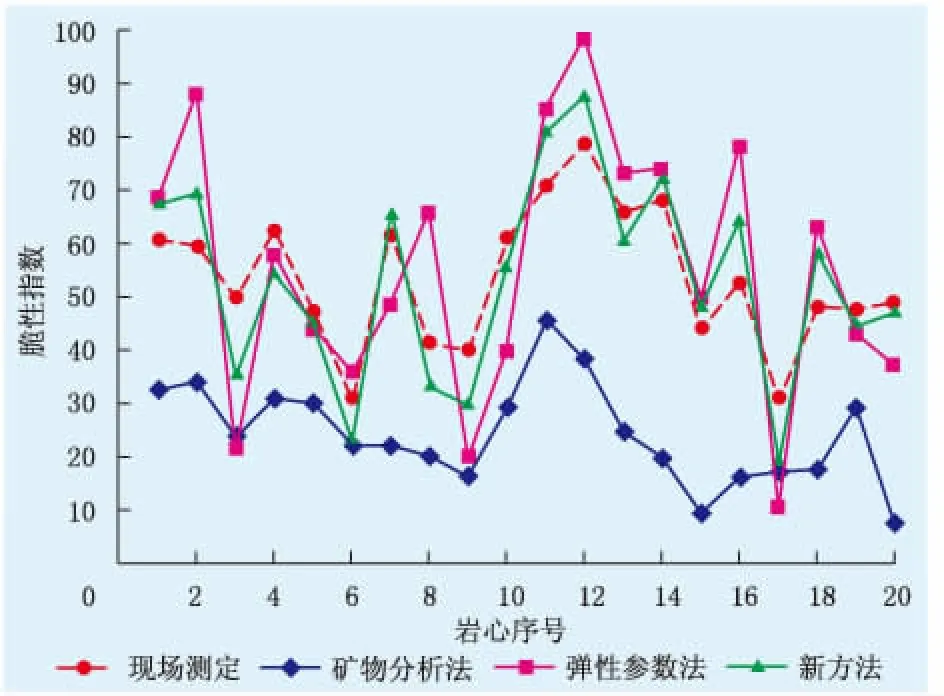
图2 不同计算方法脆性指数结果

4 结 论

(1) 针对辽河油田实际储层情况，采用逐步回归分析方法，针对不同矿物成分筛选影响岩石弹性模量、泊松比的主控因素，剔除弱影响参数，建立了岩石力学参数逐步回归模型。通过弹性参数法，并引入岩石力学参数逐步回归模型，建立了岩石脆性计算新方法。该方法可以从微观领域分析岩心脆性变化规律，并表征岩心从局部劣化至整体失稳的变化特征，实现岩心离散化后局部脆性表征。

(2) 岩石弹性模量主要由石英、方解石、方沸石、菱铁矿以及黏土的含量影响，岩石泊松比主要由石英、方解石、白云石以及黏土的含量影响。

(3) 多种岩石脆性计算方法结果与实际测定值进行了对比，新方法从微观表征岩石脆性变化规律，计算结果与现场测定结果误差最小，同时精细量化了不同矿物成分对储层脆性的影响，修正了矿物分析法计算结果与实际情况偏差较大的现象，可精确判断岩石压裂过程中的失稳破裂方位，对现场压裂施工效果分析更具有参考价值。