数学分析选讲教学的探究*

赵淑波 崔仁浩 刘萍 （哈尔滨师范大学数学科学学院数学系）

学生们感到数学难学主要原因在于没有培养好对数学分析的辩证思维、没有掌握好丰富的数学分析方法。基于分析学掌握的困难性和重要性,加之数学学习必须突出解题练习这个环节分析选讲课应运而生,其是数学分析课的后继课,是对分析课的回顾、反思,同时为学生研究生入学考试分析科目的准备起协助作用。学生们对这门课的掌握情况与教师的教学有关,教与学相伴而生,教对学具有引领功效,其作用是不言而喻的。

分析的思维是否跟得上，内容有没有掌握好,重要的检验方式是面对题是否会做,也就是数学分析的解题能力是否培养起来,解数学分析题当然也是解数学题，怎样解题？通俗说,解题就是在已知与未知之间建桥；在新知识和旧知识间建立起联系,且联系是非人为的、实质性的.利用已有知识及思维结构,对抽象的形式化思想材料进行加工,且依托思维而完成的。

解题重要,自然解题能力的培养是这门课教学的重中之重.教学的重心在于以问题为载体培养学生“学解”而不仅是给“解”；教学生如何“数学地思维”。

教学生学解数学分析题就是引导学生学习数学解题,有意义地发现学习,引导学生去探索。

一 引导学生学习“构造”,是学习解数学分析题,培养学生数学思维的重要手段

分析中关于构造的问题遍布于各章,面对涉及构造性题目,重点研究为什么这样处理优于讲怎样处理,也就是,着重谈为何这样构造,而不仅是怎么构造。数学解题是一个尝试过程,不同的尝试会悟出不同的解决方法。涉及需要辅助函数、辅助点集等的构造,多数情况,构造不唯一,多种证明方法引导开阔了同学们的解题思路。同时伴随着思维的训练。

实数几个等价的完备性定理是数学分析的逻辑基础,其应用有一定难度。这是一道考研真题。设f在[a,b]上连续,f(a)＜0,f(b)＞0。证明：存在x0∈(a,b),使得f(x0)=0且f(x)＞0,x∈(x0,b]。其证明不管是应用区间套定理还是确界原理,都需要进行构造。

首先引导学生分析：这个题目是极限理论部分关于抽象函数的特殊点的一般存在性问题。闭区间连续函数性质这类题目证明方向是多选完备性定理；选哪个定理,其实几个定理本质上是等价的,都从不同角度刻画了实数系的完备性。理论上,能用一个定理解决的,一定也能用其它定理来解决。形式上的不同又决定了同一个题目应用不同的定理证明难易程度不同。联想与该题目相关的零点定理的证明首选确界原理、区间套定理。这里我们也不妨先选二者试之。再引导学生回忆构造法证明存在性问题的常用思路,可先找到可疑点,再验证真伪。怎么找?假设法,先假设已经找到可疑点,看它所应具备的条件,然后再根据这些条件想办法构造。

对于证法一：确界原理

分析用确界原理的一般思路是先构造点集,再证确界是所找的点。要找的点是某点集的上确界,同时又是另点集的下确界,这就意味着可选的点集不唯一。怎么构造简单?假设法,假设最大零点已找到,其必是零点集的最大数也必是上确界,所以构造的点集不妨就取零点集,验证其上确界为最大数,证确界为最大数只需证确界属于集合即可。

证该问题集合的构造不唯一,同样可证出零点集的最大值点也是点集

对于证法二：区间套定理

引导学生分析：用区间套定理证题的思路是构造区间套,使得套住的点即是所求的点怎么构造?思路是由果索因,先假设点已找到,它应满足上述条件,不管怎么构造,这个点一定是区间套套住的点,现在就分析这个区间套具备的条件,套住的点是零点,所以区间套中区间必含零点,且零点右侧函数值大于零,相应的区间右侧函数值也应大于零。满足这两点构造即可。以上是以构造区间套为例来谈如何构造,类似还有构造函数、开覆盖、构造点列等。

有说法是引导学生学习构造浪费时间,我认为如果称是为了所谓的教学省时间,就算数学知识可以被动地传授给学生,但解数学题的各种典型方法、技巧、个性化解题策略和深层次蕴含的思想不可能只靠老师单纯讲解几个例题,然后学生机械模仿老师的解法,就可以获得的。单纯讲授的解题方式的培养,容易造成学生只能应付一些模式固定的问题。而难以处理灵活的题目。真正的解题能力是练出来的,而不是教出来的。学习解题好的方法就是在不断解题中学习解题,是有意义的发现学习。学习数学解题就是不断积累经验的过程,有经验的解题人会发现解决数学问题常常就在一念之间,这一念如果被攻破,问题就迎刃而解、水到渠成。比如前面提到的构造问题,区间套的构造,一旦区间套给出问题就攻克,但问题在于,这个构造是别人给出的还是自己获得的,只有自己点破,才对学习数学解题有意义,只有学习练就这种点石成金之功,才可能实现解题的宗旨。这种功夫基本不是别人教的,而是自己悟出来的。

学习数学解题,是有意义的发现学习,谈到发现,就需要学生自己去实践,实践出真知。对于实践而言,学生们已有的解题认知结构就起着决定性的作用,其包括解题知识结构、思维结构和解题元认知结构。具备一个组织良好的数学知识结构是解题者解题的必要前提。知识结构与知识储备相联系。涉及数学相关的概念、定理等,记忆里的知识被安放得井然有序会对解题有很大的帮助。这一点数学家波利亚也曾提到。

有两种方式形成数学的解题知识块,一种是按照归类的方式形成。如何归类,依照问题关键事实归类,常见如判定定理等,由此,我们将题按照解题方法进行归类,我们称它为多题一解；另一种方式是对每一类数学问题都尽可能地形成一种或几种解题思路,由此我们建议一题多解。

二 实现一题多解、多题一解是形成解题知识块的重要方式,是实现有意义发现学习的基础

学过的知识自然希望掌握扎实、应用自如。将知识结成块、形成网是实现这一想法的重要手段,如何结成块？尝试一题多解、多题一解。每每遇到问题,将其能解决的各种手段有重点的试之。比如,极限是数学分析研究的工具。以下递推数列以欧拉常数为极限,设x0=1,xn+1(1+xn)=1(n≥0)。证明：xn存在并求其极限值。证明数列极限存在的常用方法都可以试证之。极限定义、迫敛性定理、柯西收敛准则、压缩映像原理、单调有界定理、上下极限定义等多种方法证明。经验证,这些方法都可以解决此题。就一个题而言,可以多种方法处理,推而广之,一类问题的解决方案同样可以多种,如判定正项级数收敛的方法：收敛定义；柯西准则；四则运算、可结合性、可交换性；基本定理；判别法：比较、比式、根式、积分、拉贝判别法等,可根据方法和题的特点比较,逐一试之。启发学生用多种方法解决,以帮助学生学会建立解题知识块。我们可以分别将各个方法的常见考研题进行归类,总结用每一类方法的问题的特点以及用每一类方法解题的一般思路和解题步骤。

如可按照同一判定方法将下面积分不等式证明问题归类

1.设f″(x)＞0,求证 其中为任意正数

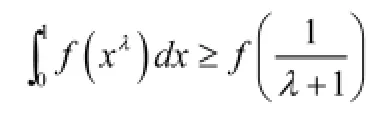
3.设φ在[0,a]上连续,f二阶可导,且f″(x)≥0,

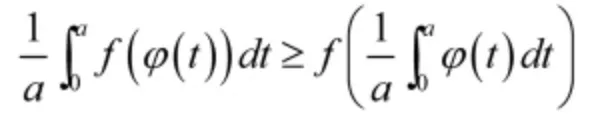
4.设f在[0,1]上二阶可导,且f″(x)≤0,求证

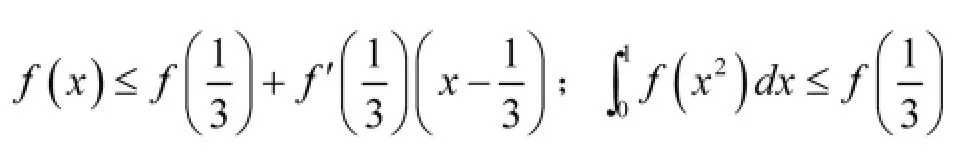
其中λ为任意正数。

形成解题知识块的重要方式是按照归类的方式形成。

这些题目形式上看似不同,但都可用凸函数、积分不等式性来证明,解题思路相同,我们称它为多题一解。会做这类题的同时掌握了该证明方法,题是无限的,但方法是有限的,学会用有限的方法解决无限的题,同时有助于形成解题知识块,这也符合数学学习需要不断提高运用抽象概况思维方法水平的特点。势必会收到事半功倍的效果。

当然,强调多题一解、一题多解的同时,方法有所侧重更是快速解决问题的必须,很多问题的解决还是有一般规律的,如在应用微分学基本定理证题时,涉及一个函数的函数值与一阶导数时,先用拉格朗日中值定理证之,遇到一个函数的函数值与二阶及以上导数时,先用泰勒公式处理之,看到两个函数的函数值与一阶导数时,首选柯西中值定理去解决。

为了培养学生的解题能力这个中心,分析选讲的教学除了从形式上看,要注意引导学生学会构造,学会一题多解、多题一解,形成解题知识块。内容上,要注意抓住核心概念与定理这两个基本点。

三 注意核心定理理解的透彻性是学会解题的关键

定理是数学知识的重要组成部分,如果把数学概念比作数学大树的根,我认为数学定理就是大树的干,有了树干才为枝叶更好地输送养分,使得枝繁叶茂,经常我们可以直接根据概念计算证明,但是根据定理计算证明有时更直接容易。应用定理处理问题,使得解决问题的深度、广度都扩大了,要想对定理更好地应用必须很好的掌握,如何掌握？深挖掘细体会,比如中值定理结论中形式上最简单的是Rolle定理的结果,这个定理给出了导函数存在零点的一个充分条件,该定理的已知要求：函数f在闭区间[a,b]上连续,但我们注意到为得同样的结论,函数值相等可推广为极限值相等。即设f在有限区间(a,b)内可导,f(a+0)=f(b-0)=A（A为有限数）,则至少存在一点ξ∈(a,b),使得f’(ξ)=0。而且a,b不但可为有限数,也可为a=-∞或b=+∞或a=-∞同时b=+∞即区间由有限区间可推广为无穷区间。而且,极限A为有限数可推广为A=+∞或A=-∞。相应的拉格朗日中值定理与柯西中值定理也可作把函数值换为极限值的推广等。

还有联系函数极限与数列极限桥梁的归结原则：在教科书中是这样叙述的。设f在U0(x0；δ)上有定义,对任何含于U0(x0；δ)且以x0为极限的数列都存在,并且相等。我们注意定理中条件极限相等是可以去掉的,定理仍然成立。一方面加深了对定理的理解应用,另一方面也显现了数学的简洁性与严密性之美。

四 掌握数学分析概念的教学是教好数学分析的前提,同时把握数学概念的本质及应用也是上好选讲课的关键

有数学分析学习的基础,分析选讲教学重心在于概念、定理的深层次理解及应用上。就概念而言,从思维的形式来看,所有的思维形式都离不开概念,概念是基础,是数学的细胞,数学分析中的概念是数学分析大厦的基石,是分析中定理与方法的源泉,根据概念证题,伴随在整个分析学习中,不论是书中定理还是习题证明都离不开它,分析的研究对象是函数、研究工具是极限。要谈概念,函数和极限当然是重中之重了,极限的ε-δ、ε-N定义,众多核心概念依其而存在的,连续、可微、可积、一致收敛、一致连续等等。还包括函数项级数的一致收敛、含参量广义积分的一致收敛等。谈如何学习概念时,经常会提到抓住其本质,那么数学概念的本质属性是什么呢？一般来说,一个特定数学对象,在一定的条件下,保持不变的性质,就是其本质属性,而可变的则是非本质属性。函数是数学分析的研究对象,它的本质属性是什么呢？函数是一种映射,要理解函数的本质其实质就是弄清映射的本质特征,映射是两个集合之间满足随处且单值定义的对应关系,而函数就是数集到数集上的对应关系,由此我们可知数集到数集上的对应、随处定义、单值定义是函数的本质特征,是函数不变的性质。

掌握了定义、定理就掌握了基本证题术中的根据定义证题术、根据定理证题术。此外,推广性命题证题术也是数学分析中常用的一种证题术,它包括仿照法、转化法、变异法。根据推广对象的特点可分为：个别向一般的推广、一维向二维的推广、离散问题向连续问题的推广、有限向无限的推广、有界向无界的推广等。

五 解题回顾是学习数学分析解题的重要环节

解题回顾从时间顺序来说,虽说是数学解题最后环节,却是解题学习的最关键步骤,针对提高学生解题能力而言,回顾解题是最有意义的环节。然而在实际教学实践中,这一点常被轻视或忽略,进而使学生错过了更多的获益机会。我们要清楚教学目的的问题,进行解题教学并不仅仅是求得所谓问题的结果,其真正目的是为了提高学生数学解题的能力,培养学生的创造性品质,而这一教学目的恰恰主要是通过回顾解题的授课来实现的,基于此,经验丰富的教师总是高度重视解题回顾这一过程的教学,师生一同对解题的最终结果和多种解法进行细致分析,对解题的主要思想和关键要素进行简要概况,帮助学生发现不足,获取经验,成为以后解题时联想的基础。检验解答、讨论解法、推广结果和思维活动反思,构成回顾解题四个方面。

讨论解法一题多解、多题一解,这一点前面已阐述,我们着重谈一下推广结果。

推广的形式多样,可以是从具体到抽象,从特殊到一般等。

设在内可微,证明：在内至少有x(1-x)f′（经-2的一个零点。

注意到：如果记g(x)=x(1-x),则1-2x=g′(x)

推广到抽象函数情形：

设函数φ,ψ在[a,b]上连续,在(a,b)内可导,且φ(x1)=ψ(x2)=0,x1、x2∈(a,b),证明：在(x1,x2)内至少有φ′(x)+φ(x)φ′(x)的一个零点。

从两个推广到多个函数情形

设函数f在[a,b]上连续,且

推广设函数f在[a,b]上连续,且存在非负整数n,使得

简要地说,回顾的不仅是相关知识、解题方法,还包括开始时怎样想的,遇到哪些问题,犯过那些错误,为什么会出现这些问题,分析对的理由,错的原因。从而不断地积累经验,经过不断的练习,会总结出自己的处理经验,就是所称的解题策略,会指导我们今后学习。同样是行得通的思路经常是不是唯一。

解题后的回顾为今后学生们的解题积累经验。在浩瀚无边的题海中,学生是爹爹不休地做题,老师是风风火火地讲题,有时我们甚至把解题回顾看成是浪费时间。正如古人所说：工欲善其事,必先利其器,解题回顾可称是磨砺解题武器的过程,别忘了我们的目标是学会解题,而不是解完所有题,解题回顾起到事半功倍的效果。

总之,不管这门课的教学手段、形式如何,教学的主旨都是为了学生能够更好地学习,学习不只是本门课程内容,更是要学会学习数学,进行数学学习。所谈的数学学习,能够认为是学生经过取得数学知识经验,而引发的持续长久行为、能力和倾向变化的过程。要想学会解题,要想掌握好数学分析,是一个综合能力的培养。需要注意做的地方很多,这里我只谈了我认为重要的且容易忽略的几点,希望和读者能有共鸣。