考虑非均匀地基原水管道受力特征模型试验研究*

孙鹏飞，汪 磊，吴奇峰，周 骏，施 亮

(1.上海工程技术大学 城市轨道交通学院，上海 201620；2.上海城投原水有限公司，上海 200127)

0 引言

上海原水管道铺设过程中往往存在区间管道下方无夯实铺平的现象，由此产生的不密实地基易导致管道发生不均匀沉降，造成管道局部应力集中。

现行规范对这方面的施工标准规定并不明确，导致经常出现输水管道爆管泄露事故，不但影响城市正常运行而且对人民生命财产安全构成威胁，所以研究地基不均匀沉降对输水管线带来的力学影响尤为重要。

高惠瑛等[1]用3次曲线描述沉陷区管道的几何变形，并通过力学变形协调条件得出沉陷区和非沉陷区交界面处的内力,从而计算出沉陷区管道各点的位移和截面内力;赵欢等[2]通过建立弹性地基梁计算模型，确定管道不均匀沉降段的应力集中区，得出不均匀沉降所产生的管道最大弯矩、挠度等值；张土乔等[3]建立合理力学模型，并通过C语言编程进行分析计算，得出地基差异沉降对管道的纵向力学性状产生巨大影响的结论;蒋宏业等[4]采用ABAQUS软件分析了不同壁厚、管径和内压条件下管道的受力规律，最终确定了管道最大受力位置;张陈蓉等[5]从工程堆载的地层响应角度出发,通过模型试验与有限元分析，验证了堆载对管道施加的表观荷载可分为直接应力与位移2种形式的假设，提出堆载下埋地管线响应的Winkler模型简化计算方法。虽然上述研究成果解决了许多地下管线施工问题，但是工程现场环境复杂，许多理论上的成果缺乏足够验证，并不适用于实际工程，尤其在非均匀地基条件下原水管道受力特征方面没有进行有效的试验研究，因此，有必要采用室内模型试验方法对非均匀地基条件下原水管道进行研究。

导致地基不均匀沉降的原因较多，比如管道埋置施工质量差、地铁开挖、地下水位沉降等[6]，但是，地基不均匀沉降形式可分为地基不均匀区域在长度、宽度、深度范围内几何尺寸的变化和密实程度的变化。本试验基于白金汉原理和量纲分析法，通过缩比例尺模型试验，结合工程实况，使地基不均匀区域宽度和深度保持不变，针对土体沉降区域长度和密实度的变化进行管道应力实时监测，可为不均匀地基区域内输水管道受力特征的研究提供理论和试验依据。

1 模型试验概况

1.1 工程背景

本文以上海市长江引水三期管道工程为背景，原水管道埋置在以粉质黏性土为主的地层中，管顶上方覆土厚度在1.0～2.5 m之间，原水管道采用Q235钢材，其外径为2 400 mm，弹性模量为209 GPa。

1.2 相似比确定及模型箱尺寸设计

本次模型试验主要研究非均匀地基长度和密实度变化条件下的原水管道受力特征问题，故以控制几何相似比系数为主要指标，在前人研究成果[7-9]的基础上，由量纲分析法确定几何相似比为1/30，重度相似比为1。

参考相关文献[10-13]得知，大直径埋地管线的扰动范围在两侧4倍直径和下部3倍直径区间内，拟采用外径2.4 m的输水管道，根据几何换算，可得到模型试验的管线外径为80 mm，因此管线左右两侧0.32 m、下方0.24 m的部分为扰动范围，设计的模型箱尺寸应大于该扰动范围，为了满足这一要求，本试验采用的模型箱尺寸为：长1.2 m、宽1 m、高1 m，如图1～2所示。

图1 模型箱 Fig.1 Model box

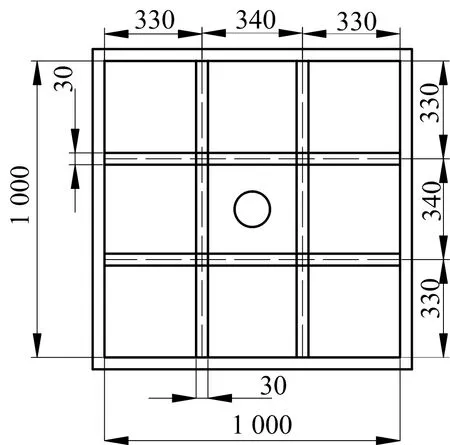
图2 模型箱示意Fig.2 Schematic diagram of model box

1.3 试验材料

1.3.1 试验管道材质

根据1/30的几何相似比常数，对实际工程采用的Q235钢材进行几何和刚度上的换算，通过多次比选最终确定采用PVC管道，其外径为75 mm，壁厚为2.5 mm,长度为2 000 mm。

1.3. 2 标准砂材料

考虑到地基不均匀程度和密实度，在管道的正下方铺设不同体积的标准砂，用来模拟管道下方的非均匀地基。标准砂采用中国ISO标准砂，其主要物理指标见表1。

1.3.3 土体材料

本模型试验采用的填料来自原水管道施工现场，经筛选破碎制备成所需的重塑土。根据原水管道埋置深度土层的地质资料，再结合在土工实验室进行的重塑土物理力学性能测试，最终确定其物理参数：含水率为30%、黏聚力为15 kPa、重度为19 kN/m3、内摩擦角为22°、压缩模量为3.2 MPa，具体操作如图3所示。

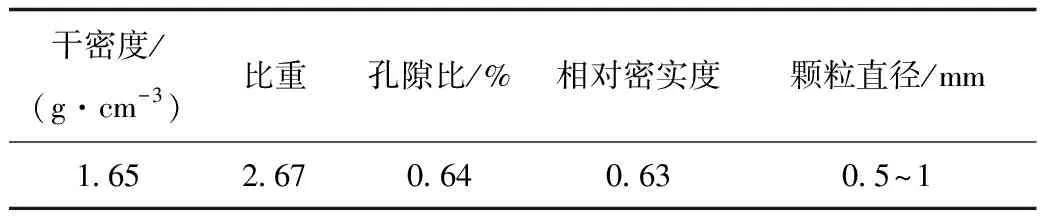
表1 标准砂物理参数Table 1 Physical parameters of standard sand

图3 重塑土物理参数测试Fig.3 Tests on physical parameters of remolding soil

1.4 试验加载数值的确定

原水管道外径为2.4 m，管顶覆土厚度取最大值2.5 m，根据几何相似比换算，确定本模型试验采用外径为75 mm的PVC管，管顶上方堆放90 mm厚的重塑土。管道在实际使用过程中承受的荷载主要有管道自重、管道围压和地表堆载等，可通过在土体上方施加砝码模拟地表堆载。

根据模型箱尺寸设计出长0.9 m、宽0.55 m的矩形加载板，用来将砝码的重量均匀分布在土体上，加载板位于模型箱的中央。通过对施工现场的考察，确定了堆载在管道上方土体的高度为2～8 m，本试验选取堆载土体高度为3,6,9 m，假定覆土的重度为20 kN/m3，按照1/30的相似比进行换算，得出不同堆土高度下的加载重量，具体的换算过程见表2。

1.5 试验步骤与工况

1)将施工现场的土样进行筛选破碎，加入适量的水并充分搅拌配备成含水率为30%的重塑土，在模型箱内铺设重塑土来模拟管道周围土体。在铺设过程中，每铺设50 mm厚的土体层进行1次压实，控制重塑土密度为1.9×103kg/m3，直至填筑高度到达管底标高处。根据文献[14-16]研究的模型试验对不均匀地基区域尺寸进行划分，选取试验管道的直径作为划分的尺度。由调研现场施工情况得知，管道下方非均匀地基长度的范围在0.6～5 m之间，宽度约为3 m， 最大沉陷深度约为0.4 m,由于原水管道直径为2.4 m，因此本模型试验不均匀地基宽度取1.2D，深度取0.2D，长度选取1D，1.5D，2D作为代表值，其中，D为管道外径。为了模拟管道在非均匀地基条件下的受力状况，在模型箱的正中央位置先挖出长宽高分别为1D，1.2D，0.4D大小的非均匀地基，如图4所示。根据1/30的几何相似比，可以反推算该尺寸的孔洞对应的是实际塌陷区域长宽高分别为2.4，2.8，0.96 m的状况。

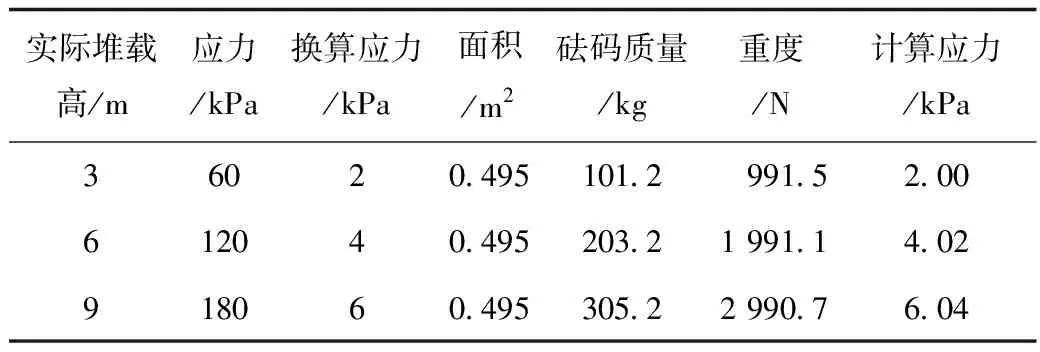
表2 试验加载值换算

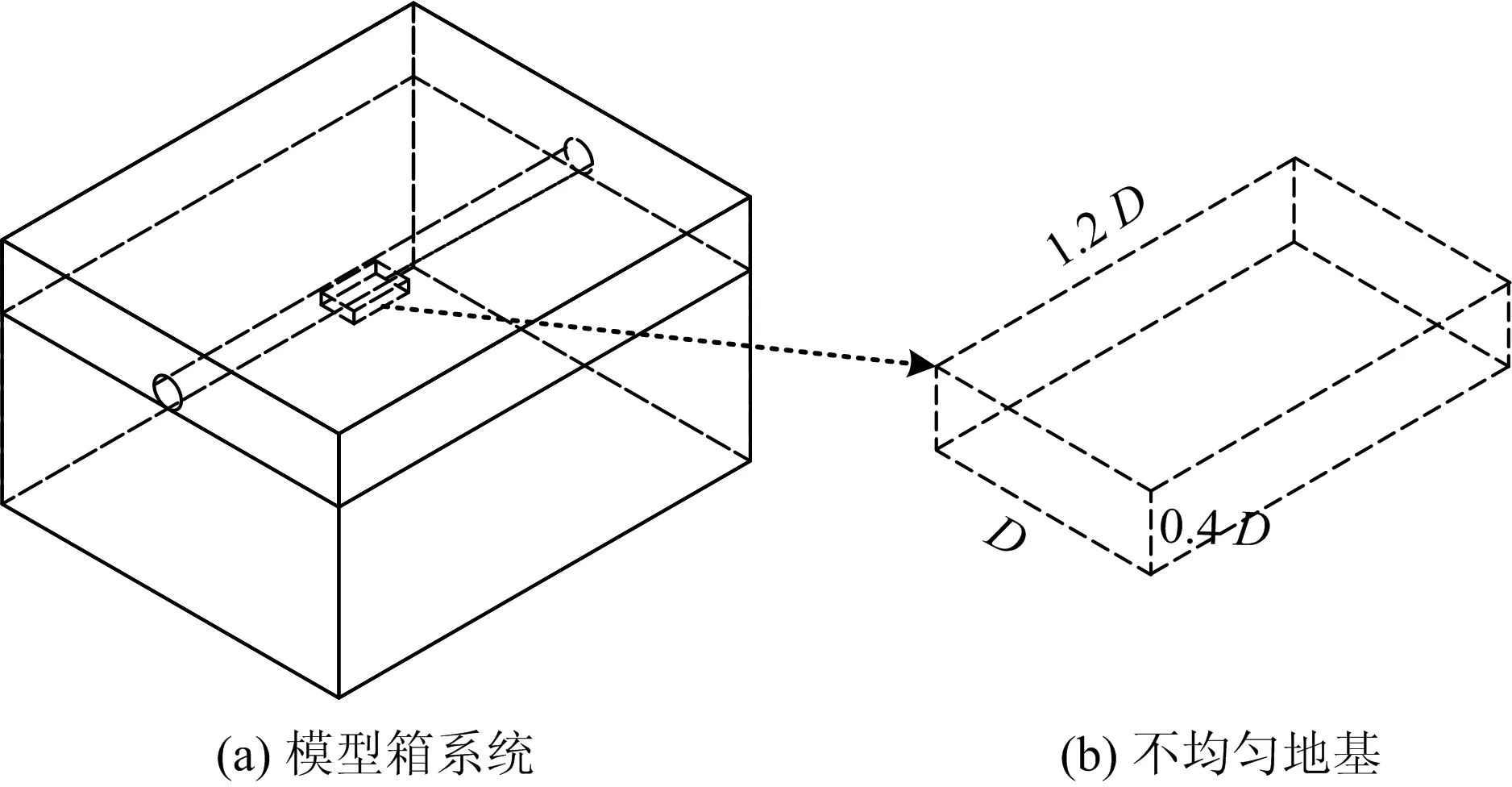
图4 不均匀区域示意Fig.4 Schematic diagram of non-uniform area

2)将应变片粘贴到管线上已经标记好的位置，用硅胶进行防水并用绝缘胶进行固定，把贴好应变片的管道安装至模型箱预定的位置，把应变片导线连接到静态应力数据采集仪上，继续填土至管顶上方90 mm标高处。

3)将加载板放置在模型箱的中央位置并依次放置砝码进行加载试验，并在电脑端实时采集数据。

本次实验分别完成了非均匀地基长度为1D，1.5D，2D3种工况，另外，通过虚铺标准砂模拟管道下方局部存在软弱下卧层的工况，最后，作为参照完成了均匀地基条件下的模型实验，具体工况见表3。

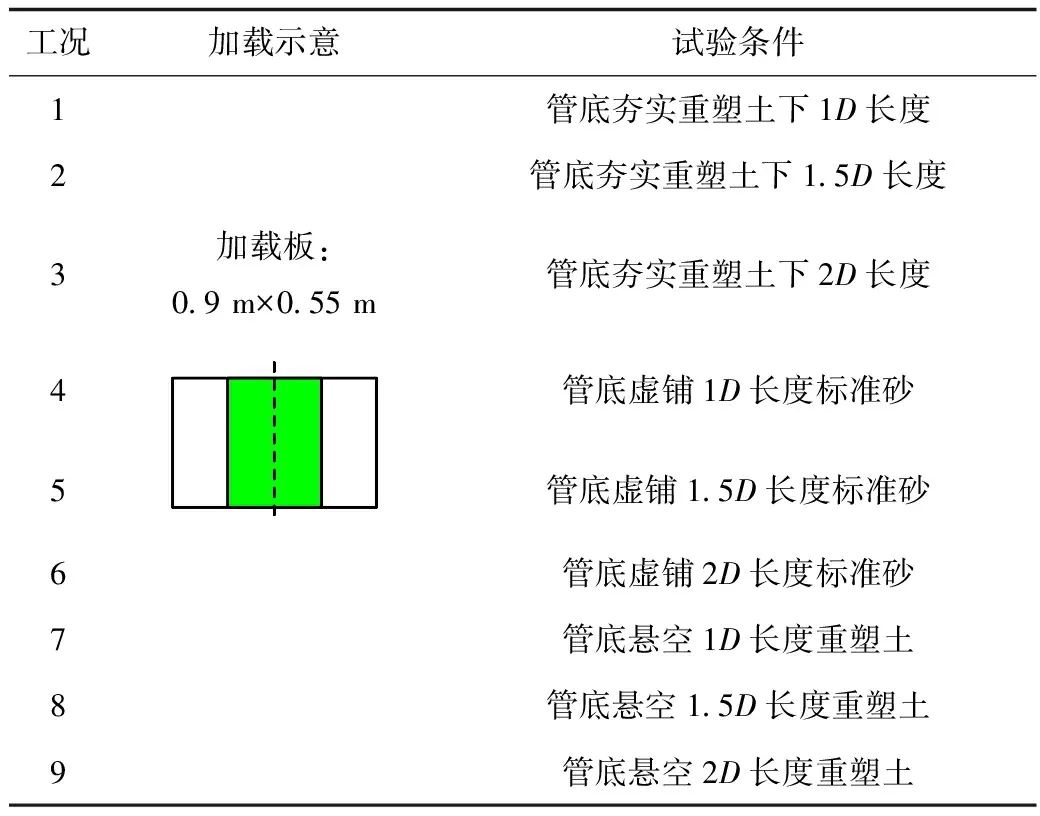
表3 试验工况

1.6 测点标号

应变片粘贴在非均匀地基边缘截面处和管道中央截面处的位置，截面标号如图5所示，在Ⅰ，Ⅱ，Ⅲ截面处沿着管道的轴向分别在管顶、管腰、管底处粘贴应变片。图5中的第Ⅰ和第Ⅲ断面的位置仅代表孔洞长度为2D的情形，应变片具体的粘贴位置随着挖孔长度的变化而变化。为了方便记录和分析数据，对不同位置处的应变片进行标号，如图6所示，比如在第Ⅰ断面处，管顶处标记为Ⅰ-1，管腰处标记为Ⅰ-2，管底处标记为Ⅰ-3，其余断面处的应变片标号以此类推。

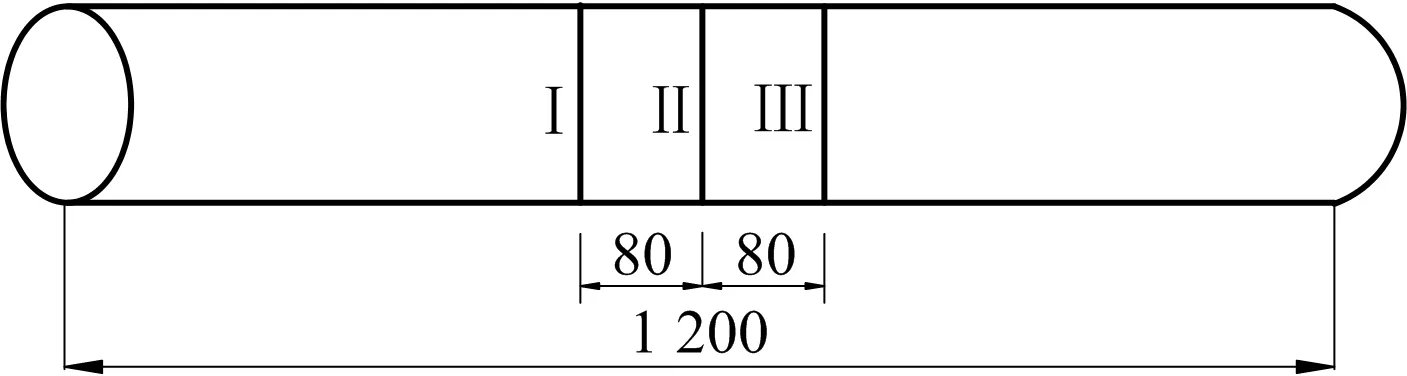
图5 截面标号Fig.5 Section numbers

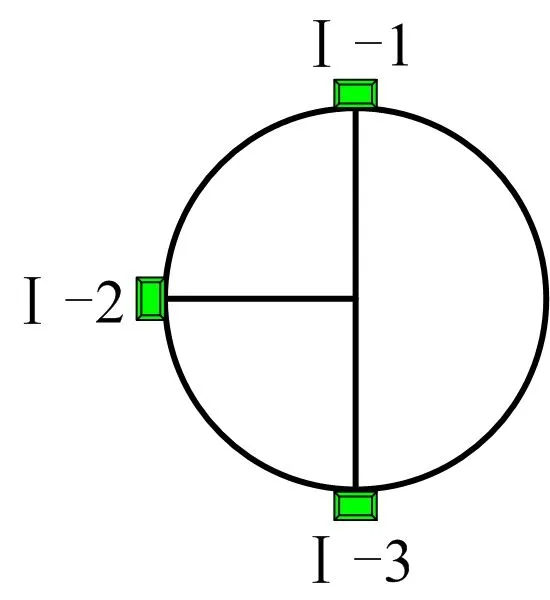
图6 应变片标号Fig.6 Strain gauge label

2 试验数据分析

本次模型试验加载形式为中心对称加载，非均匀地基区域关于管道中间截面Ⅱ对称，截面Ⅰ和Ⅲ的应变片粘贴位置关于截面II轴对称分布，二者的测点应力值大小相近、变化规律一致，因此，试验数据分析取截面Ⅰ和Ⅱ进行分析。为更清楚分析截面Ⅰ和Ⅱ上测点的应力变化情况，将测点在所有工况下的应力值以折线图的形式展现。

2.1 实测值与有限元计算值比较

2.1.1 有限元模型介绍

为了验证本次模型试验的准确性，利用MIDAS GTS-NX软件对PVC管道进行数值模拟计算。地基土模型尺寸为长1.13 m、宽0.93 m、高0.69 m，其中留出非均匀地基和管道的配合位置，管道与土体相互作用过程中选用Mohr-Coulomb进行计算，并且选择板单元模拟管道模型，模型管密度为1.34×103kg/m3,泊松比为0.3。对管道和土体施加重力场，管道两端设为固支，土体四周沿各自的法线方向不能移动，定义好对称边界条件；作用在管道上的荷载为矩形均布面荷载，加载板长1.1 m,宽0.45 m；荷载大小分别为2，4，6 kPa。

2.1.2 有限元计算值与实测值对比

选择性的提取测点在工况1～9中6 kPa条件下的试验应力值，并且与对应的有限元值进行对比，如图7所示(图中实线代表实测值，虚线代表有限元值)，二者应力值误差率在10%以内，应力值变化的规律较好地吻合，论证了模型试验结果的可靠性。

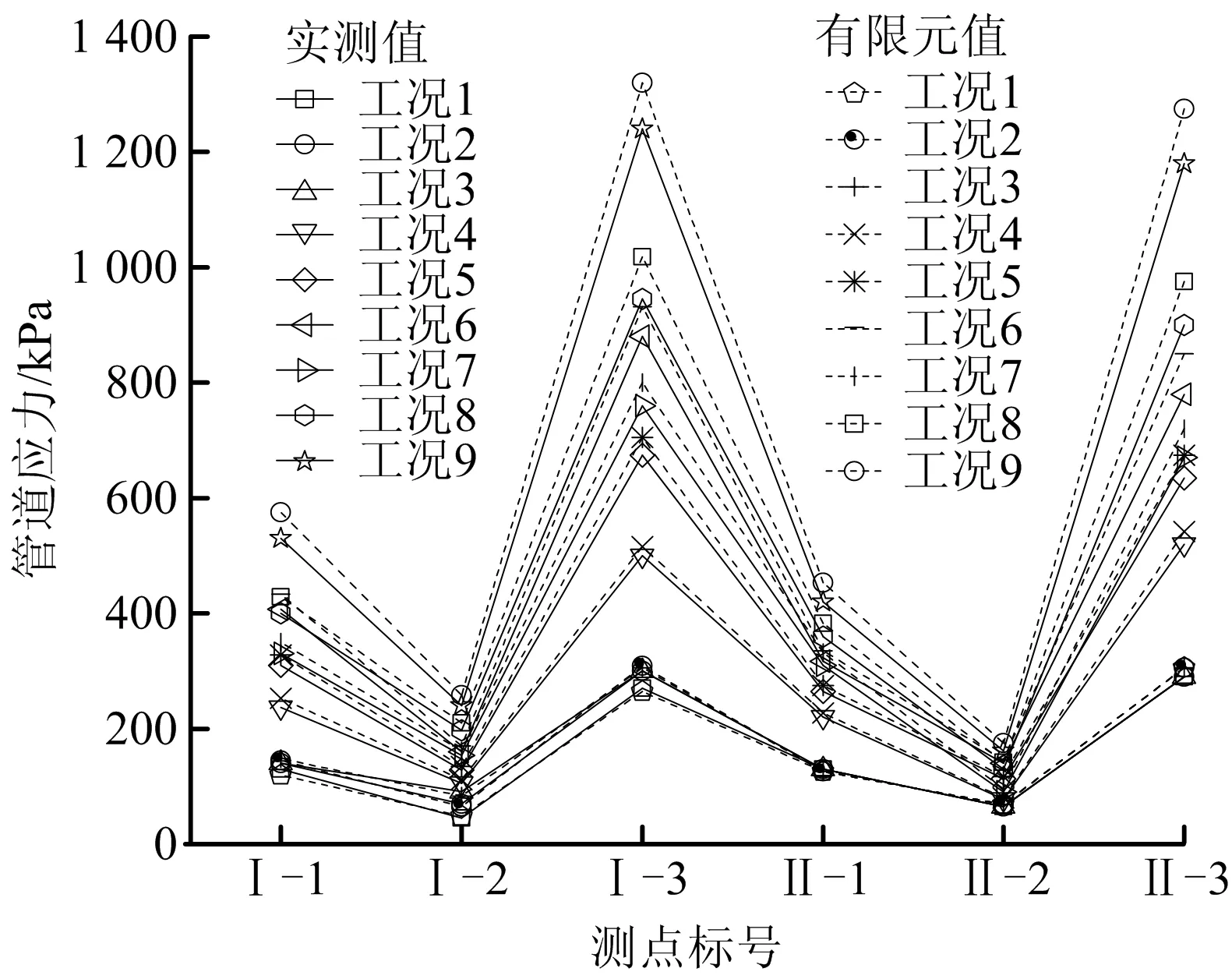
图7 有限元值与实测应力值对比 Fig.7 Comparison of finite element values and measured values

2.2 试验实测值分析

截面I上测点应力值的变化情况如图8～10所示。其中，I-1测点位于截面I的顶部，对其工况4～6进行分析，当非均匀地基长度从1D变为1.5D，1.5D变为2D时，平均应力增量分别为28%和30%，在工况7～9中这一比例分别增大为25%和36%，管底虚铺标准砂下的应力增幅大小与管底悬空下的相差甚微。对比均质密实地基与非均匀地基条件下的应力值可以看出：1D长度下，工况1～4和工况1～7的平均应力增量分别为149%和216%；1.5D长度下，增量为192%和260%；而在2D长度下，增量为280%和391%。随着不均匀地基长度的增加，管道应力值增幅总体呈现出逐渐增长的趋势。

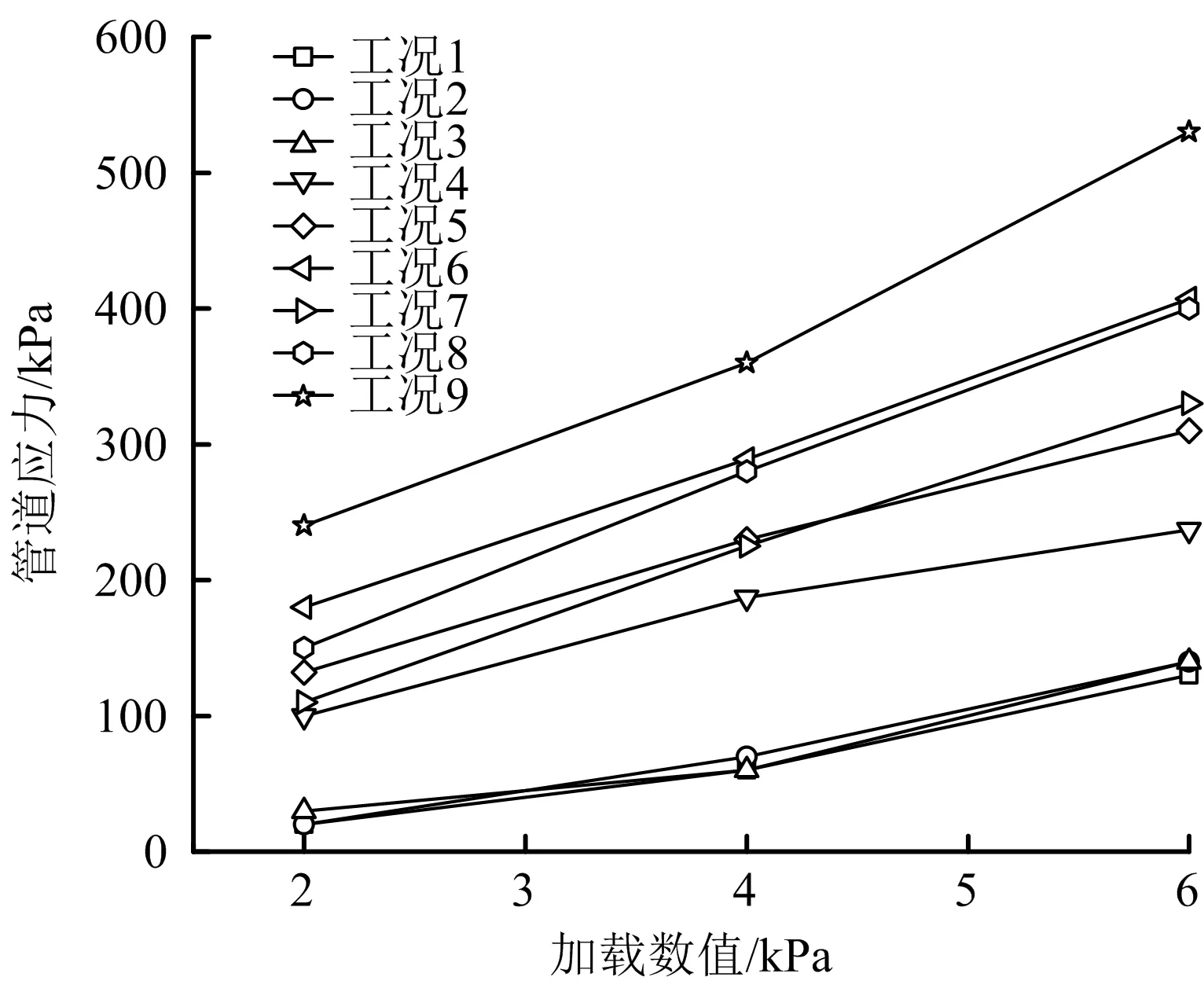
图8 测点Ⅰ-1应力变化Fig.8 Stress change of measuring point Ⅰ-1

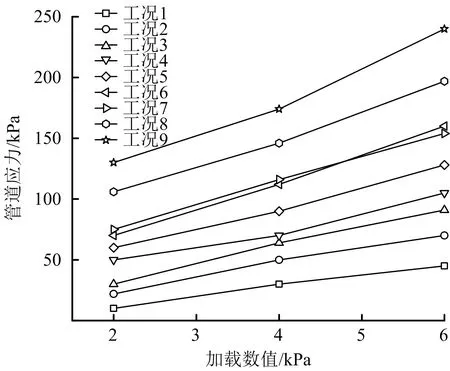
图9 测点Ⅰ-2应力变化Fig.9 Stress change of measuring point Ⅰ-2

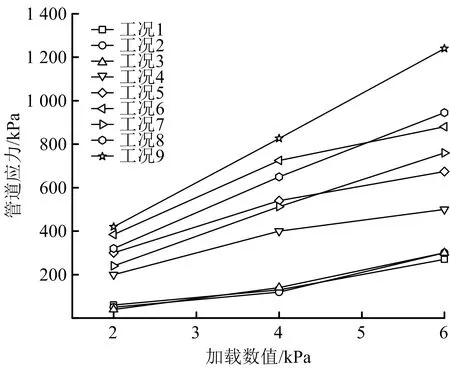
图10 测点Ⅰ-3应力变化Fig.10 Stress change of measuring point Ⅰ-3

同理对Ⅰ-2和Ⅰ-3测点采用上述方法进行管道应力值分析发现：Ⅰ-2测点处均匀地基至不均匀地基的应力值增幅小于Ⅰ-1，而Ⅰ-3测点的增幅大于Ⅰ-1。同时对比3个测点最大应力值看出：Ⅰ-1，Ⅰ-2和Ⅰ-3测点最大应力值都出现在工况9中6 kPa条件下，分别为570，240，1 340 kPa，因此管底处受非均匀地基密实度与长度的影响最大，表现为应力数值和增幅均最大，管顶次之，管腰处受影响最小，所以应力值也最小。这是因为本试验非均匀地基的沉降形式为“凹形”，两侧地基土相对稳定，由于堆载形式为正中央加载，当管道穿越“凹形”沉降区域时发生明显的梁式受压变形，因此管道轴向的中截面挠曲变形最大，测点越远离中截面，其形变越小，管顶和管底的测点都位于中截面且管底形变大于管顶，所以呈现出以上规律。

截面Ⅱ上3个测点的应力变化如图11～13所示，由图11～13可知，应力值大小依然满足管底最大、管顶次之、管腰最小的规律。当管底地基密实均匀时，对比测点Ⅱ-1和Ⅰ-1，Ⅱ-2和Ⅰ-2，Ⅱ-3和Ⅰ-3的应力值，发现在相同条件下截面Ⅱ上的整体应力值略大于截面Ⅰ，这是因为截面Ⅱ位于管道的正中央，根据梁式受压管线变形特征，管道断面Ⅱ处的竖向位移最大，并且截面Ⅰ和Ⅱ的距离相对于加载区域的管线长度较小，二者的竖向位移相近，因此应力值大小和变化规律均相似。在管底虚铺标准砂和悬空时对比2个截面的应力值发现：不均匀地基长度为1D时，加载值为2 kPa，截面Ⅱ的应力值大于截面Ⅰ的应力值，加载值为4 kPa和6 kPa，截面Ⅰ的值则与截面Ⅱ的值相近；非均匀地基长度大于1D时，无论加载值多大，截面Ⅰ的值始终比截面Ⅱ的大，且随着不均匀地基长度增加和加载值增大，二者的差距也在变大。这是因为均匀地基与不均匀地基交界处的介质错位对该位置的管道产生拉伸作用使其发生膨胀，进而产生上拱状的形变，且该截面自身又受到管道梁式变形的作用，所以截面Ⅰ受二者的叠加影响，因此非均匀地基长度越长加载值越大，这种叠加影响越明显，截面Ⅱ与截面Ⅰ值的差距越大。

另外，在不均匀地基长度相等的条件下，对比截面Ⅰ和Ⅱ上测点的数值发现：在加载值较小时，管道下方悬空测得的应力值与管底虚铺标准砂的应力值相近，随着加载值的不断增加，二者应力值的增速出现不同且二者的差距在不断变大，主要是因为在加载初期，标准砂的可沉陷量大，可能与管底悬空一样出现“管土分离”的现象；加载后期，标准砂可压缩空间不断减小且密实度增加导致管道变形受阻，应力值增速减缓，因此与管底悬空工况下的值相比差距愈加显著。

非均匀地基对管道的应力影响较大，尤其对管底的作用较为明显，为了保证管道的安全，建议施工单位在铺设管道时采取对管底的加固措施，并且注意回填土地基的回填质量。

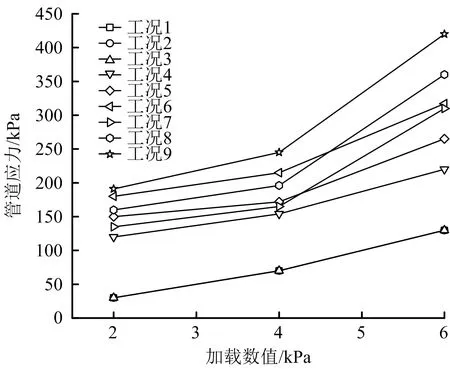
图11 测点Ⅱ-1应力变化Fig.11 Stress change of measuring point Ⅱ-1

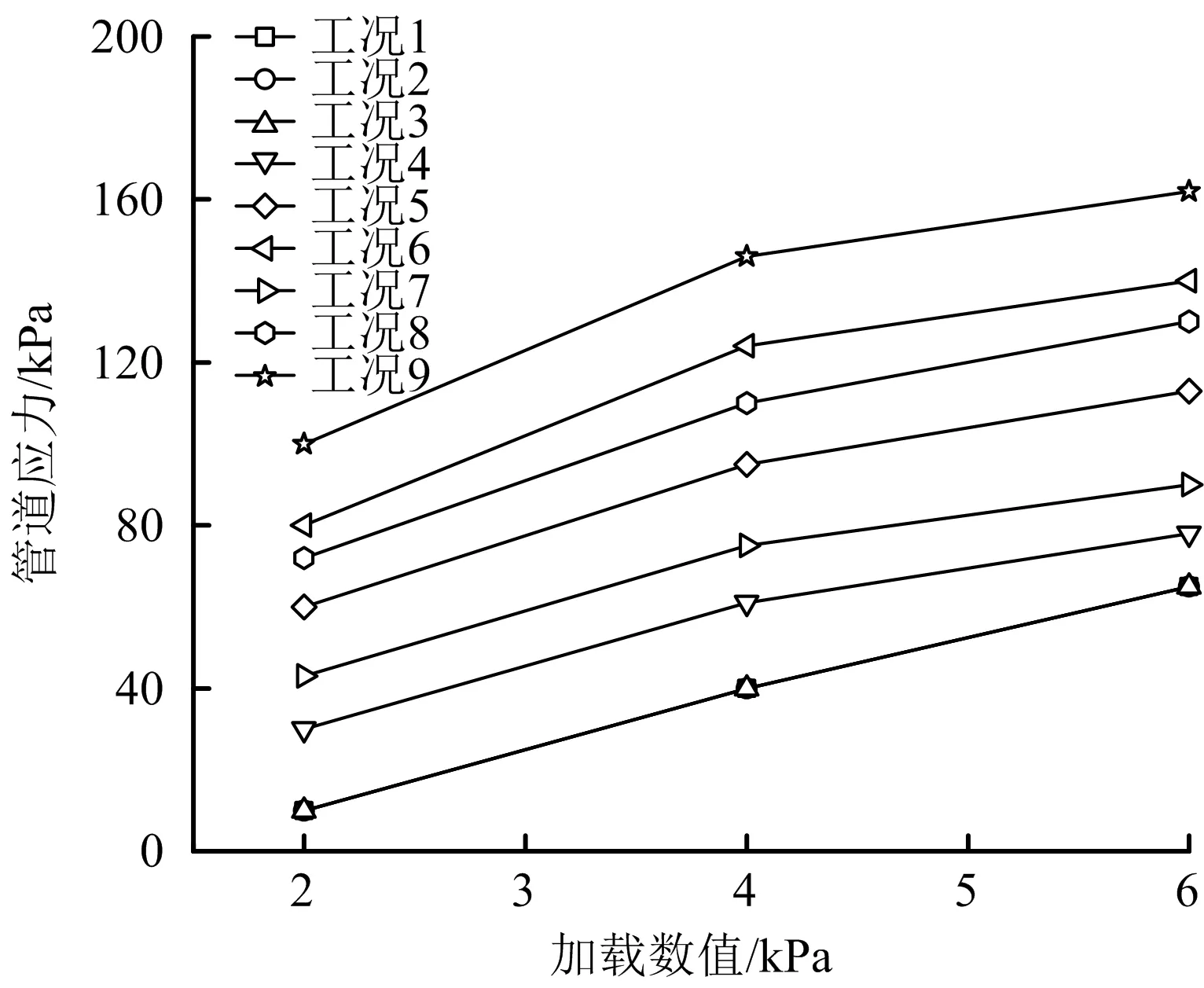
图12 测点Ⅱ-2应力变化Fig.12 Stress change of measuring point Ⅱ-2

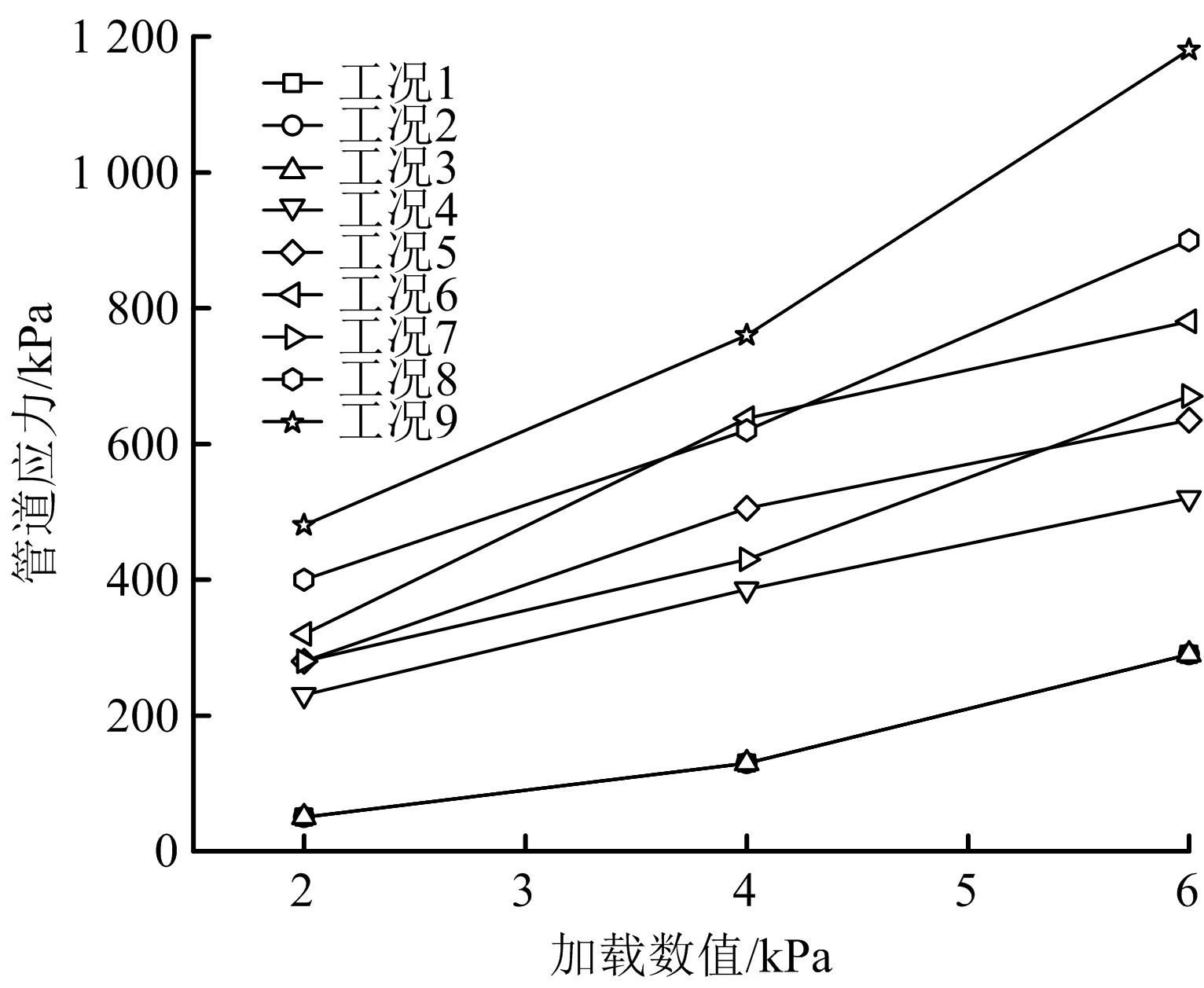
图13 测点Ⅱ-3应力变化Fig.13 Stress change of measuring point Ⅱ-3

3 结论

1)地基的密实度对管道应力值有很大影响，呈现出密实度越高管道应力值越低的规律。管底虚铺标准砂条件下的应力值比管底压实下的应力值平均大2.7倍左右，管底悬空下的值则比管底压实下的值大4.2倍左右。另外，管底虚铺标准砂下的管道应力值随着加载值增加，前期增速比后期要快；而管底悬空时，应力值的增速则呈现出后期比前期快的趋势。

2)非均匀地基的长度是影响管线最大应力截面位置的关键因素。长度为1D时，截面Ⅱ上测点的整体应力值略大于截面Ⅰ上相同位置处的应力值；长度为1.5D和2D时，截面Ⅰ大于截面Ⅱ上的应力值。由此可以预测：随着非均匀地基长度的增加，管道最大应力截面位于均匀地基与非均匀地基的交界处，且长度越长，该截面所受应力越大。

3)无论管道埋置在均匀密实地基区域还是非均匀地基区域，同一截面上的3个测点在相同条件下，都呈现出管底处应力值最大、管顶次之、管腰处最小的规律，因此在铺设管道时建议施工单位特别注意对管底的质量监测，尽量夯实铺平地基，对容易产生不均匀沉降的地基段加强质量监控，出现问题及时采取补救措施。