基于IEEMD样本熵分析的管道泄漏定位*

朱一龙，邢志祥，郝永梅，吴 洁，严欣明，岳云飞

(1.常州大学 环境与安全工程学院，江苏 常州 213164；2.江苏特种设备安全监督检验研究院常州分院，江苏 常州 213161)

0 引言

城市管道发生泄漏往往会造成较大的经济损失及环境污染，甚至可能危及人身安全。因此，管道泄漏检测技术受到广泛关注，并得到快速发展。目前，管道泄漏检测方法主要有声发射检测法、压力梯度法、负压波法等，其中声发射检测法凭借其灵敏度高、适应性强等特点得到广泛应用[1]。但声发射信号中混杂有大量噪声，定位误差大，需对其进行信号处理，处理方法有小波阈值去噪、经验模态分解、奇异值分解等。然而以上方法都存在的缺陷有：小波阈值去噪会在重构信号时产生振荡，容易丢失有用信号[2]；经验模态分解存在模态混叠、端点效应等缺点[3]；奇异值分解通过逆变换重构信号，虽然有较好地去噪效果，但计算效率过低[4]。

针对以上不足，提出1种改进的集合经验模态分解(Improved Ensemble Empirical Mode Decomposition，IEEMD)样本熵分析的管道泄漏定位法。运用改进的集合经验模态分解处理管道原始泄漏信号，得到各阶信号分量；然后采用样本熵(Sample Entropy，SampEn)分析法对各阶信号分量优选重构，获得有效泄漏信号；最后结合互相关时延计算对泄漏点进行精确定位。

1 泄漏信号提取

1.1 IEEMD信号分解

EEMD(集合经验模态分解)是1种针对非线性、非平稳信号的分析方法，此分析方法将信号分解为一系列振荡函数，强大的自适应特征使其广泛应用于信号处理领域[5]。但EEMD存在2个问题：1)分解后的信号模态中仍残留噪声分量和冗余分量；2)运行时间过长[6]。

针对以上问题，在EEMD中添加自相关函数计算和EMD过程，提出IEEMD算法。已知在EEMD过程中，高频噪声信号分量会被首先分离出来，且噪声信号的自相关函数具有快速衰减到零的特点。因此，通过计算各阶信号分量的自相关函数识别噪声信号分量(判断噪声分离与非噪声分离的分界)。当这些会引起模态混叠噪声信号分量被识别、分离后，剩余信号无需再进行完整的EEMD分解，于是改用EMD对剩余信号分解，旨在节省时间、提高信号分解效率。IEEMD算法的具体步骤为：

1)在管道原始泄漏信号x(t)中加入1对符号相反的白噪声，添加白噪声的对数为N，得到2N个添加白噪声后的信号：

(1)

式中：mi(t)为第i个添加白噪声后的信号；x(t)为原始泄漏信号；ni(t)为添加的第i个白噪声信号；“+”和“-”表示符号相反。

2)利用EEMD筛分原理分解mi+(t),mi-(t)，得到2N个一阶信号分量ui,+1和ui,-1。原始泄漏信号x(t)第1个信号分量u1为2N个一阶信号分量的集成平均值，即：

(2)

3)计算u1的自相关函数，判定其是否为噪声信号分量。若是噪声信号分量，继续进行下一步迭代；若不是噪声信号分量，停止迭代。

4)对剩余函数ri+(t)及ri-(t)进行更新，并作为新的分解对象重复以上步骤，得到第2个信号分量u2：

(3)

5)当第p个信号分量up不是噪声信号分量时，停止迭代。从原始泄漏信号x(t)中减去步骤1)～ 4)中得到的p-1个信号分量后，改用EMD分解剩余信号，最终可得到：

(4)

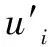
1.2 基于样本熵的有效泄漏信号选取

Shannon第1次将熵的概念引入到信号处理中，证明熵与信息内容的不确定程度有等价关系，并把此种不确定程度称为信息熵[7]。Koimogorov在此基础上，提出K熵[8]。但K熵计算条件要求苛刻，对噪声过于敏感。基于此，Pinus提出了抗噪能力强的近似熵，并取得良好效果[9]。但近似熵存在自匹配问题，导致其计算结果依赖于数据长度。为了克服这一缺点，Richman提出样本熵[10]，其算法比近似熵更简单，计算量更小，所需时间更短。同时，由于克服了自匹配问题，样本熵对数据长度的依赖更小。

根据样本熵上述特点，将样本熵作为管道泄漏故障信息提取的特征参数。任意x(t)={x(1),x(2),…,x(N)}的样本熵计算过程为：

1)由信号序列构成1个m维向量：

(5)

2)定义xm(i)和xm(j)之间的距离：

(6)

3)给定容限r，统计每个xm(i)对应的d[xm(i),xm(j)]≤r的数目，记为Ai。把Ai与N-m+1的比值记为：

(7)

4)求出Bim(r)的平均值Bm(r)：

(8)

5)用同样的方法求出Bm+1(r)，则该时间序列的样本熵定义为：

(9)

经过IEEMD分解后，真实信号分量中还夹杂有冗余分量，冗余分量会干扰真实信号提取的完备性，必须将其剔除[11]。通过计算各阶信号分量样本熵实现信号分量的优选重构：样本熵值越大，对应其非稳定时间序列的复杂程度越高，即片段中包含的有效泄漏信息越多；冗余分量表现为周期震荡函数，其复杂程度不高，即样本熵值较低。因此，选择样本熵值较大的信号分量重构，即：

h(t)=ua+ub+…+un

(10)

式中：h(t)为有效泄漏信号；ua,ub,un为优选的信号分量。

2 泄漏定位方法

2.1 互相关时延计算

互相关时延法是计算2个信号相关性的常用方法[12]，采用互相关时延法分析时间延迟与频率之间的关系，进而计算得到上、下游有效泄漏信号到达2个传感器的时差Δt。

互相关时延计算管道泄漏信号时差的具体步骤为：

1)利用IEEMD分解法，分别得到上、下游有效泄漏信号h1(t)和h2(t)；然后计算2个有效泄漏信号的互相关函数：

(11)

式中：τ代表2个信号的时间延迟。

2)根据互相关时域分析图中最大相关峰值计算得到2路有效泄漏信号时差Δt：

Δt=M×fs

(12)

式中：M为得到的互相关函数中幅值最大相关峰所对应的采样点数；fs为信号采集仪器设置的采样频率。

2.2 声发射时差定位法

管道泄漏定位采用声发射时差定位原理进行计算[13]，见式(13)：

(13)

式中：x为被检测管道泄漏点的位置，即泄漏点到上游传感器距离，m；L为上下游传感器之间距离，m；Δt为泄漏信号到达2个传感器的时间差，s；v为泄漏信号在管道中的传播速度，m/s。

3 管道多点泄漏试验

3.1 试验简介

试验现场有3根100 m长的钢制管道，其规格由上至下依次为DN65,DN90和DN150。本文选取管径为DN65的钢管作为研究对象，并通过空气压缩机向管内提供0.3 MPa的恒定低压气流，以模拟管道正常运行，如图1所示。

图1 管道试验系统Fig.1 Pipeline test system

3.2 有效泄漏信号的提取

本文通过声发射检测系统采集管道泄漏原始数据，主要设备包括：1台美国PCA32通道声发射采集仪、2条光缆和2个PXR04高灵敏度声发射感器。其中，1号传感器位于管道首端0 m处，2号传感器位于管道末端100 m处，在距管道首端49 m处的位置设有1个直径为2.0 mm的泄漏孔，如图2所示。

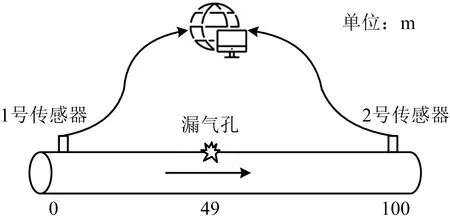
图2 模拟管道试验系统Fig.2 Simulated pipeline test system

通过声发射传感器接收管道泄漏信号并由光缆传递至声发射采集仪，通过声发射采集仪控制管道泄漏原始数据的采集、显示、分析和保存。将声发射采集仪的采样精度设置为8 bit，采样点数设置为2 048，采样频率设置为100 kHz，待管内气体平稳流动时采集管道泄漏原始数据。随机提取1组数据进行处理分析，其上游原始泄漏信号x1(t)如图3所示。

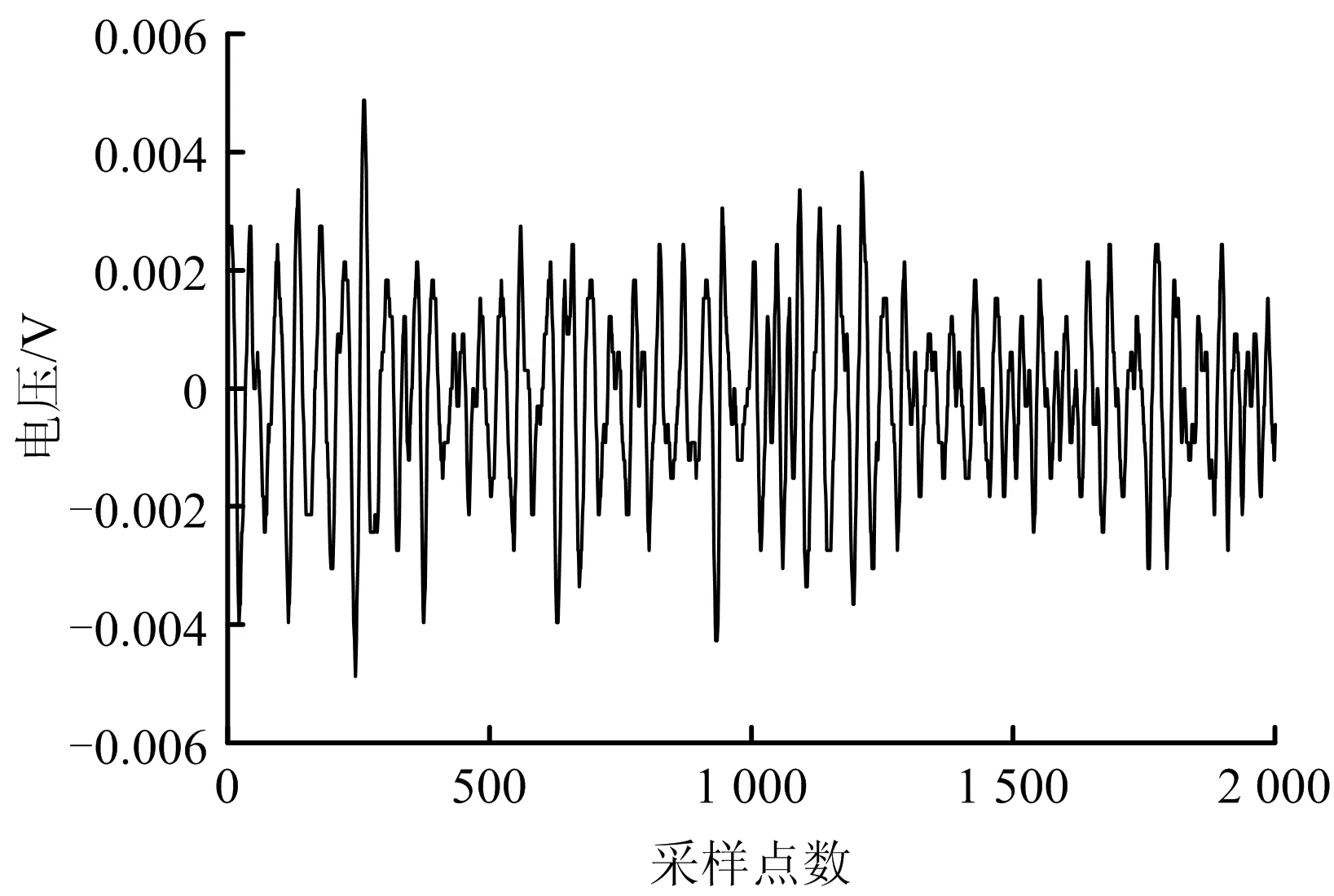
图3 上游原始泄漏信号Fig.3 Upstream original leakage signals

通过IEEMD分解，将上游原始泄漏信号x1(t)自适应地由高频到低频分解为8阶信号分量，如图4所示。计算1～8阶信号分量的样本熵，结果如图5所示。

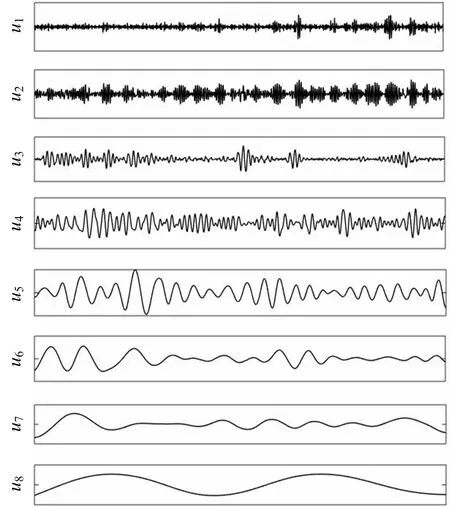
图4 上游原始泄漏信号IEEMD分解Fig.4 IEEMD decomposition of upstream original leakage signals

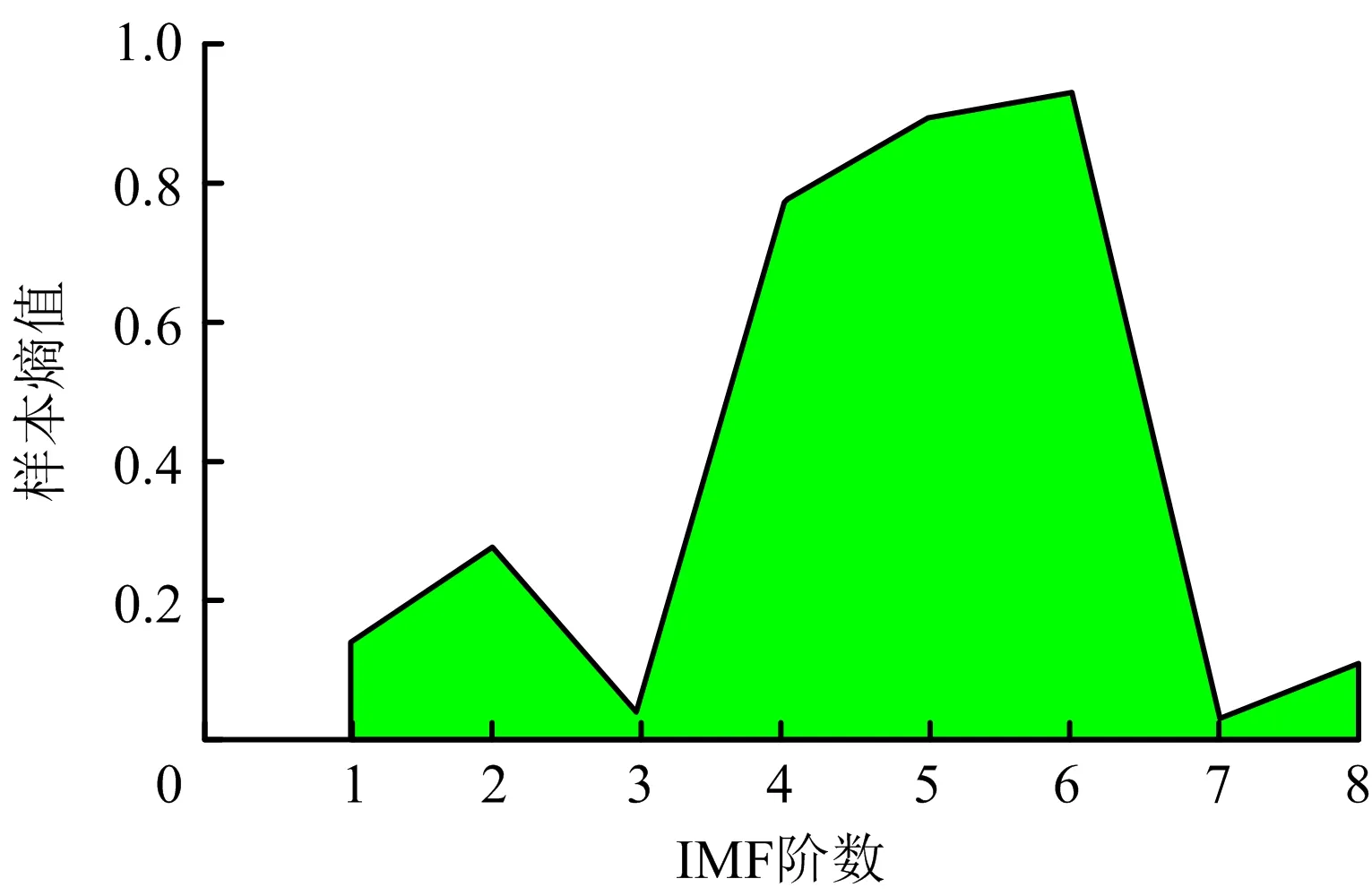
图5 样本熵计算结果Fig.5 Calculation results of sample entropy

由图5可知，前3阶信号分量的样本熵值较小，均在0.3以下；4～6阶的样本熵值较大，几乎接近于1；7～8阶的样本熵值非常小，可忽略不计。因此，根据基于样本熵的有效泄漏信号选取法对各阶信号分量优选，选择4～6阶信号分量重构获得上游有效泄漏信号h1(t)，如图6所示。

图6 上游有效泄漏信号Fig.6 Upstream effective leakage signals

同理，对下游原始泄漏信号同样进行如上所述的处理，得到下游有效泄漏信号h2(t)。

3.3 泄漏定位计算

根据互相关时延与声发射时差定位法，通过互相关时域分析计算上、下游有效泄漏信号h1(t),h2(t)的时差，结果如图7所示。

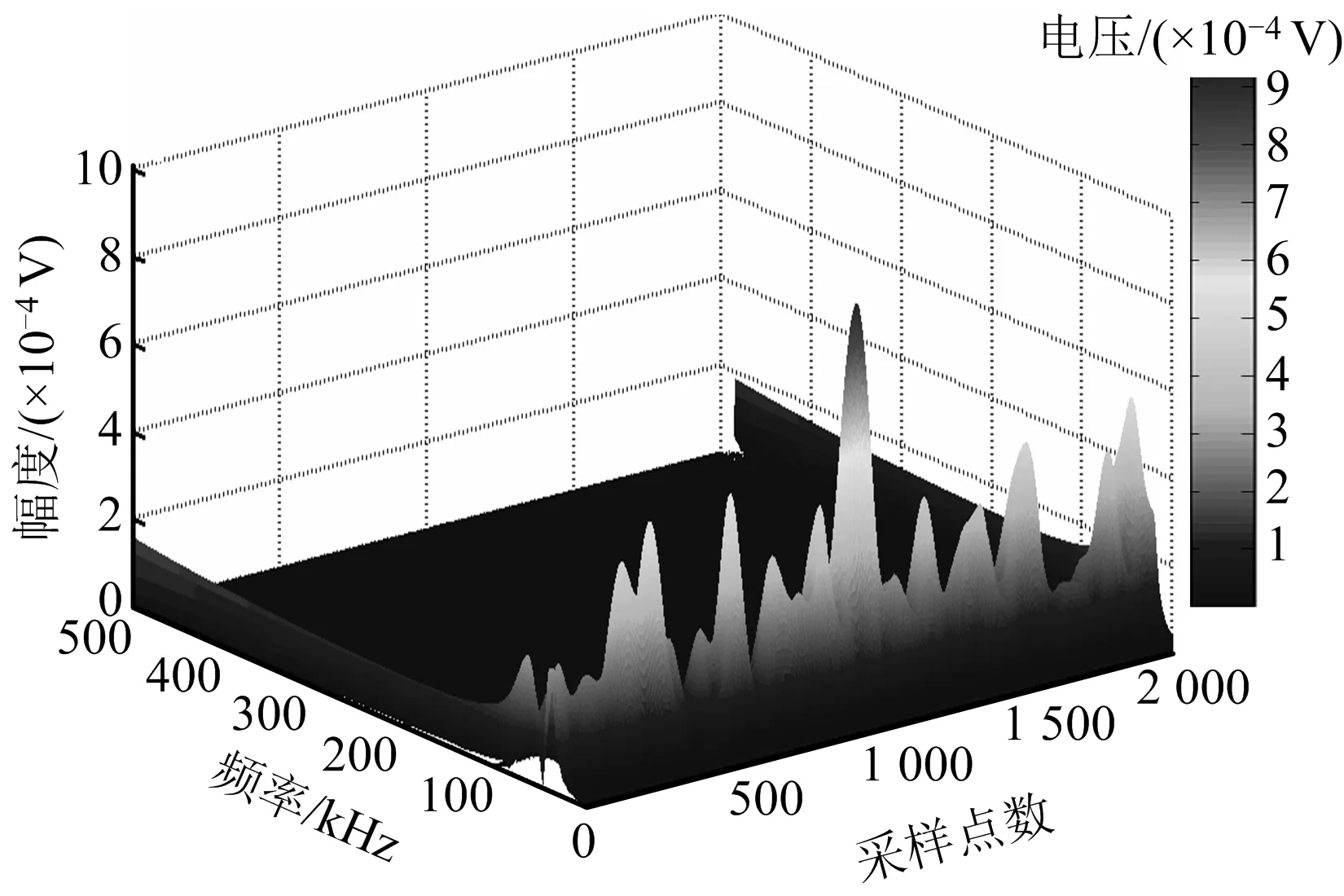
图7 互相关时域分析Fig.7 Cross-correlation time domain analysis

由图7可知，在0～400 kHz频率范围内，采样点数为963时幅值相关峰取得最大值，即互相关时延计算所需的采样点数M=963。

将采样点数M=963代入式(12)求得上、下游有效泄漏信号时差Δt=0.009 63 s，再将时差Δt和管道泄漏声速v代入式(13)即可精确计算泄漏点位置。

管道泄漏声速v不仅受管道材质的影响，还受到不同输送介质、不同运行工况的影响，且使用不同方法检测到的泄漏声速都有所差别。目前，国内外尚未形成统一的泄漏声速计算方法，各研究人员检测计算得到的数值也不一致。根据沈功田《声发射检测技术及应用》[14]可知，压缩空气介质所产生的声发射波在钢制管道中的传播速度为850～1 050 m/s，并通过大量实验对典型管道泄漏声速进行了测量，其中对1根95 m长的DN65钢制管道的测量与本文工况基本一致，最终确定其声速平均值为980 m/s。于是，根据式(13)计算得到泄漏点精确位置，即x=(100-0.009 63×980)/2=45.28 m。

3.4 结果对比与误差分析

本文采用基于IEEMD样本熵分析的方法提取有效泄漏信号，影响有效泄漏信号提取结果的因素较多，选择不同分解尺度，设定不同阈值，提取到的有效泄漏信号均不同[15]。

为验证所述方法的信号提取效果，针对章节3.2中的上游原始泄漏信号x1(t)，采用3种方法进行有效泄漏信号提取，并采用信噪比(SNR)和均方误差(RMSE)指标对提取效果进行衡量，3种方法及有效泄漏信号提取效果对比结果见表1。其中，SNR为衡量真实信号与噪声之间所占比例大小的指标，RMSE为反映原始泄漏信号与有效泄漏信号之间差异程度的度量。

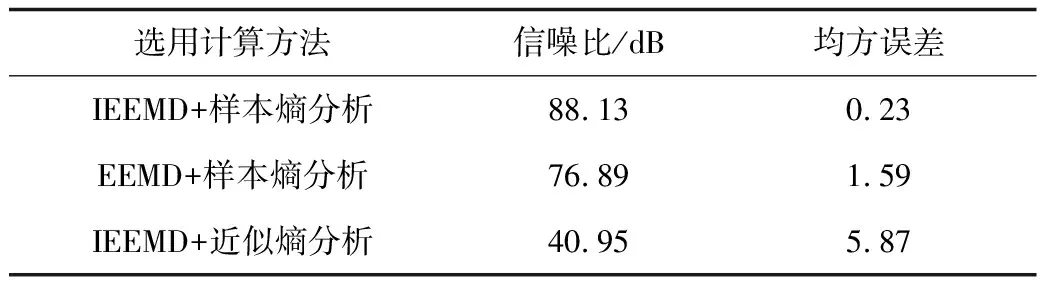
表1 有效泄漏信号提取效果对比Table 1 Comparison on extraction effect of effective leakage signals

由表1可知，3种信号提取方法的SNR和RMSE指标均不同。IEEMD+样本熵分析法(本文方法)的SNR指标最大且RMSE指标最小。这说明经本文方法处理后，信号中真实信号所占比例最大，且该信号与原始泄漏信号的相关程度最大，即本文方法有效泄漏信号提取效果最好。

为进一步验证所述方法的泄漏定位效果，随机选取30组声发射原始泄漏信号，仍采用表1的3种方法进行泄漏定位并计算其相对定位误差，结果如图8所示。

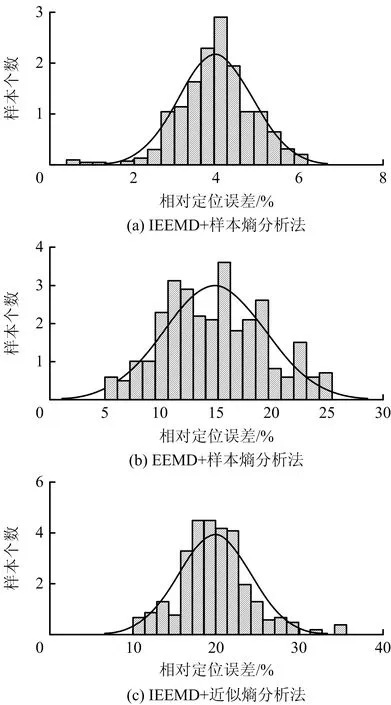
图8 相对定位误差统计汇总Fig.8 Statistical summary of relative localization error

由图8可知，3种定位方法相对误差大小有明显区分。本文提出方法(IEEMD+样本熵分析法)的平均相对定位误差4.06%；传统EEMD分解与样本熵分析相结合的方法平均相对定位误差15.23%；IEEMD分解与传统近似熵分析相结合的方法平均相对定位误差20.17%。对比结果表明，本文提出的基于IEEMD样本熵分析的管道泄漏定位方法与其他方法相比精度明显更高。

4 结论

1)针对管道泄漏信号的混杂性、易受噪声干扰性而造成泄漏定位精度低的问题，提出基于IEEMD样本熵分析的管道泄漏定位方法。

2)采用IEEMD与样本熵分析结合的方法提取有效泄漏信号，有效提高了信号的信噪比，降低了信号的均方误差。

3)基于IEEMD样本熵分析的泄漏定位法可将定位误差降低至4.06%，实现了管道泄漏精确定位。

4)该方法以圆孔为模拟泄漏点，未考虑泄漏孔形状、大小对定位的影响，可作为进一步研究方向。