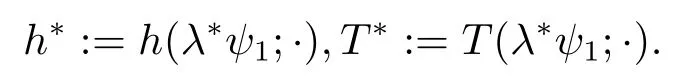Global Existence and Blow-Up of Solutions in Reaction-Diffusion System with Free Boundary
WANG Zhongqian(王忠谦),JIA Zhe(贾哲) YUAN Junli(袁俊丽),YANG Zuodong(杨作东)
( 1.Mathematics and Information Technology School,Jiangsu Second Normal University,Nanjing 210013,China; 2.School of Mathematics Science,Nanjing Normal University,Nanjing 210023,China; 3.School of Mathematical Science,Huaiyin Normal University,Huaiyin 223300,China; 4.School of Teacher Education,Nanjing Normal University,Nanjing 210097,China)
Abstract: This paper is concerned with a free boundary problem for the reactiondiffusion system with coupled nonlinear reaction terms.For simplicity,we assume that the conditions and solutions are radially symmetric.At first,we give the local existence and uniqueness of the positive solution.Then,we consider the blowup property and the long time behavior of the solution.When m2−m1 >−1,n1−n2 >−1 ,the solution blows up if the initial value are large enough.
Key words: Reaction-diffusion system; Free boundary; Blow up; Global fast solution;Global slow solution
1.Introduction
In this paper,we deal with the following reaction-diffusion system with coupled nonlinear sources and free boundary:

wherer=h(t)is moving boundary to be determined,h0>0,m1,n2≥0 andm2,n1>0,d,βandρare positive constants,and the initial functionsu0,v0satisfy

Recently,the free boundary problem has got much attention in many areas.For example,the decrease of oxygen in a muscle in the vicinity of a clotted blood vessel in [5],the American option pricing problem[6,9],tumor growth[10]and the dynamics of a population[13].Furthermore,the well-known Stefan condition has been used in the model of many applied problems.For instance,the melting of ice in contact with water[3],the spreading of species[11].
In [12],ZHANG et al.considered the following equation with nonlocal superlinear term:

They proved the local existence and uniqueness of the solution,and also studied the blowup property and the long time behavior of the solution.
In 2016,YUAN[8]studied the following model:

She extended the same idea to coupled parabolic system with higher dimension and heterogeneous environment.
A corresponding work in a fixed domain with Dirichlet boundary condition can be found in [4,7],which studied the following reaction-diffusion system

The system(1.5)is usually used as a model to describe heat propagation in a two-component combustible mixture.Hereuandvrepresent the temperatures of the interacting components,thermal conductivity is assumed constant and equal in both substances,and a volume energy release given by some powers ofuandvis supposed.
In this paper,we consider the coupled reaction-diffusion system (1.1)and pay much attention to the blowup property and the long time behavior of global solution.Here,we give some definitions as [1].IfTmax=∞,andh∞:=limt→∞h(t)< ∞,then the solution is called global fast solution,whose decay rate is exponential; while ifTmax=∞,andh∞:=limt→∞h(t)=∞,it is called global slow solution,whose decay rate is at most polynomial.
In Section 2 ,we prove the local existence and uniqueness of the solution to problem(1.1)and give the comparison principle.Then the blow-up property is studied in Section 3.At last we devote Section 4 to a discussion of the long-time behavior for global fast solution and slow solution.
2.Preliminary Results
In this section,we first prove a local existence and uniqueness result for a general free boundary problem by applying the contraction mapping theorem.Then,we obtain some comparison results,which will be used in the other sections.
Consider the following general free boundary problem:

wheref(u,v),g(u,v)≥0,f(0,v)=g(u,0)=0 for anyu,v ∈R+,andu0,v0are as in (1.2).
Theorem 2.1Assume thatfandgare locally Lipschitz continuous in R2+.For any given (u0,v0)satisfying (1.2)and anyθ ∈(0,1),there exists aT >0 such that the problem(2.1)admits a unique solution

Moreover,

whereDT:={(t,r)∈R2:t ∈(0,T],r ∈(0,h(t))},CandTonly depend onh0,θ,||u0||C2([0,h0]),||v0||C2([0,h0])and the local Lipschitz coefficients off,g.
ProofMotivated by [15],we make the transformation:

Then the problem (2.1)can be turned to the following model

Letk:=−h0β(u′0(h0)+ρv0′(h0))and

where ∆T:=[0,T]×[0,h0].It is trivial to verify thatMT:=YT ×ZT ×HTis a complete space with the metricM,here

Noticingh1(0)=h2(0)=h0forh1,h2∈HT,we can easily deduce

Sincefandgare locally Lipschitz continuous,there exists a constantLdepending on||u0||C([0,h0])and||v0||C([0,h0])such that



has a unique bounded solutionand

whereC1is a constant which depends onθ,h0,L,||u0||C2[0,h0]and||v0||C2[0,h0].Now,we define(t)by the fourth equation in (2.4):

A simple computation gives that

Next we define the mapping




Applying theLpestimates and Sobolev’s imbedding theorem again,we get

Similarly,we have

whereC3,C4depend onC1,C2and the local Lipschitz coefficients off,g.Moreover,

In virtue of (2.11),(2.12)and (2.13),and lettingT ≤1,we get

whereC5depend onC3,C4andβ,ρ,h0.Because of the triangle inequality and the facthi(t)≥h0,h′i(t)h0≤k+1,we have


by (2.14)and (2.15),we obtain

Remark 2.1Sinceum1vn1andum2vn2are bounded for anyu ∈YT,v ∈ZT,from the proof of Theorem 2.1 ,we can deduce that the problem (1.1)have a unique solution (u,v,h)such that (2.2)and (2.3)hold.
Next,we give the monotone behavior of the free boundaryh(t).
Lemma 2.1[15]The free boundaryh(t)for the problem (2.1)is strictly monotone increasing,that is,for any solution in (0,T],we haveh′(t)>0,for t ∈(0,T].
Next,we consider the problem (1.1)and give the comparison principle.
Lemma 2.2(The Comparison Principle)Suppose thatm2−m1>−1,n1−n2>−1,and suppose thatT ∈(0,∞),∈C1([0,T])andwith


then the solution (u,v,h)of (1.1)satisfies
16. This was a fairy, who had taken the form of a poor country woman: Fairies or other magical beings are frequently disguising themselves in order to test the mettle39 of characters in fairy tales. In some variations with a strong Catholic influence, the woman may be the Virgin40 Mary or another saint. In some Russian variants, the benevolent character is God himself.Return to place in story.

whereDTis defined as in Theorem 2.1.
ProofMotivated by Lemma 3.4 in [15],we can deduceh(t)≤(t)for allt ∈(0,T].Sincem2−m1>−1,n1−n2>−1,we can apply the usual comparison principle (Lemma 3.1 in [4])overΩT:= {(t,x)∈R2:0 In this section,we discuss the blow-up behavior of the solution to problem(1.1).First we give the following definition. Definition 3.1IfTmax<∞and or then we say that (u,v)blows up in finite time. Theorem 3.1Let [0,Tmax)be the maximal time interval in which the solution (u,v,h)of (1.1)exists.IfTmax<∞,then (u,v)blow up. ProofIn order to complete the proof of our Theorem,we suppose that,whenTmax<∞, then there existK1,K2such that||u||L∞([0,h(t)])≤K1< ∞,||v||L∞([0,h(t)])≤K1< ∞andTmax≤K2for anyt ∈[0,Tmax). Motivated by[15],we first prove thath′(t)is uniformly bounded in(0,Tmax),that meansh′(t)≤K3,withK3independent ofTmax.Firstly,we define for some appropriateKover the region: Then we will chooseKso thatp(t,x)is a upper solution.Direct calculations show that,for(t,r)∈ΩK, Assumem1+n1≥m2+n2.It follows that Thus,if we chooseKsuch that Then applying the maximum principle tou−pandv−p,respectively,we can obtain thatu(t,r)≤p(t,r),andv(t,r)≤p(t,r)for (t,r)∈ΩK.Thusur(t,h(t))≥pr(t,h(t))=−2KK1andvr(t,h(t))≥pr(t,h(t))=−2KK1.Therefore, At last,we only need to proveu0(r)≤p(0,r),v0(r)≤p(0,r)forx ∈[h0−K−1,h0].Since we can get that if Thus,we only need to choose Sinceh′(t)are uniformly bounded in [0,Tmax),there exists a constantK4which depends onK1,K3such that||u(t,·)||C2([0,h(t)])≤K4and||v(t,·)||C2([0,h(t)])≤K4fort ∈[0,Tmax).In view of Theorem 2.1 ,we can find aτ >0 depending onK1,K3,K4and extend the solution of the problem (1.1)with the initial timeTmax−τ/2 toTmax+τ/2,which contradicts the definition ofTmax.We have thus proved the theorem. In what follows,we will give the blowup conclusion of the solution of (1.1). Theorem 3.2Assume thatm2−m1>−1,n1−n2>−1.Let (u,v,h)be a solution of the problem (1.1),then the solution (u,v)of the problem (1.1)blows up for sufficiently large initial data. ProofConsider the following auxiliary problem: Sincem2−m1>−1,n1−n2>−1,by using the comparison principle,we can deduce that,on[0,h0]×(0,T].On the other hand,according to Theorem in[7],we know thatwill cease to exist at a finite time for large initial data.Therefore,the blowup result also holds for (u,v).The proof is complete. Although the above theorem provides a sufficient condition to the finite-time blowup,the condition for the initial datau0(x),v0(x)is very rigid.Next,we try to find some other specific conditions aboutu0(x),v0(x). Theorem 3.3Assume thatm2−m1>−1,n1−n2>−1 andn1m2+(m1−1)(1−n2)>0.Let(u,v,h)be a solution of problem(1.1),andψ1(r)be the first eigenfunction of the problem hereψ1(r)>0 inBh0and||ψ1||L∞=1.Then the solution of the problem (1.1)with the initial functionu0(r),v0(r)in the form ofMψ1(r)blows up in finite time ifMsatisfies ProofIfm1+n1≤m2+n2,according to the inequality (2.2)of Theorem 2.3 in [4],we getut−d∆u ≥C2um1+σn1,whereσ:=Letbe the solution of We assert thaton (0,T]×[0,h0)by using the usual comparison principle. Next,we prove thatblows up in finite time.Sincen1m2+(m1−1)(1−n2)>0,n1−n2>−1 ,it is easy to calculate Multiply the first equation of (3.8)byψ1,then integrating over [0,h0]and using Jensen’s inequality,we obtainF′(t)+dλ1F(t)≥C2(F(t))m1+σn1,whereF(t):=Aswe havewhich implies thatuwill blow up in a finite time,so does.Therefore,(u,v)blows up in finite time. Similarly,we can get the corresponding result for the casem2+n2≤m1+n1.The proof is complete. In this section,we attempt to find global fast solution and slow solution.At first,we give the existence of a fast solution by the following theorem. Theorem 4.1Assume thatm2−m1>−1,n1−n2>−1 andmi+ni >1(i=1,2)hold.Let (u,v)be a solution of the problem (1.1).If (u0,v0)is small in the following sense: thenTmax=∞.In addition,h∞< ∞,and there exist real numbersC,δ >0 which depend onu0,v0satisfying||u0||L∞,||v0||L∞≤Ce−δtfort ≥0,respectively. ProofIt suffices to construct a suitable global super-solution.Motivated by [2,15],we define We setδ:=andIt follows that Assuming(4.1)holds and choosingϵ:=2 min {||u0||L∞,||v0||L∞},we get(r)>u0(r)(r)>v0(r)forr ∈[0,h0].By applying the comparison principle,one can see that ifu,vexists.Moreover,we can get that (u,v)exists globally from (3.1)and (3.2). Next we prove a priori estimate for the global solution. Lemma 4.1Assume thatm2−m1>−1,n1−n2>−1 andn1m2+(m1−1)(1−n2)>0 hold.Let (u,v)be a solution of problem (1.1)withTmax=∞andh∞< ∞.Then there exists a constantC=C(||u0||C1+θ,||v0||C1+θ,h0),such that whereCremains bounded for||u0||C1+θ,||v0||C1+θandh0bounded. ProofIfm1+n1≥m2+n2,using the inequality (2.1)of Theorem 2.3 in [2],we have By the usual comparison principle,we have thatis an upper solution of problem (1.1).Next,we prove that Sincen1m2+(m1−1)(1−n2)>0 holds, By Proposition 3.1 in [15],we get thatsatifies so does (u,v). Similarly,we can conclude the corresponding boundness for the casem1+n1≥m2+n2.The proof is complete. Lemma 4.2Assume thatm2−m1>−1,n1−n2>−1 andn1m2+(m1−1)(1−n2)>0 hold.Let (u,v)be a solution of the problem (1.1)withTmax=∞andh∞<∞.Then Next,we give the existence of a slow solution by the following theorem. Theorem 4.2(Slow Solution)Assume thatm2−m1>−1,n1−n2>−1 andmi+ni >1(i=1,2)hold.Letψ1(r)be the first eigenfunction of the problem (3.6).Then there exists a positive constantλ,such that the solution (u,v)of (1.1)with initial datumu0=λψ1,v0=λψ1is a global slow solution. ProofWe denote the solution of(1.1)by(u(u0;·),v(v0;·))to emphasize the dependence of (u,v)on the initial data.Inspired by [1],we define By Theorem 3.3 and Theorem 4.1,we haveΣis bounded and not empty.Let Sincemi+ni >1(i=1,2),m2−m1>−1,n1−n2>−1,we haven1m2+(m1−1)(1−n2)>0.So the condition of Lemma 4.2 holds. According to the method of Theorem 4.2 in[15]and combining Lemma 4.2 and Theorem 4.1 here,we can deduceh∗∞=∞,T∗=∞.The proof of the theorem is now complete.3.Finite Time Blow-Up



















4.The Global Fast Solution and Global Slow Solution