相对熵结合互信息的高光谱波段选择方法

袁博，胡冰

(1.南阳理工学院 计算机与信息工程学院，河南 南阳 473004；2.南阳理工学院 学报编辑部，河南 南阳 473004)

0 引言

研究发现，光谱往往在很大程度上表征了地物的本征特性[1]，光谱分辨率的提高有助于对地物的精确识别和分类[2]。然而，高光谱遥感数据的数据量大、冗余信息多，高光谱影像处理算法普遍具有约束条件多、运算量大、计算复杂等特点，为了降低计算复杂度并改善处理精度，不仅需要从原始数据中提取地物光谱信息，还应该在保留原始光谱结构与有效光谱信息的前提下，尽可能减少参与运算的数据量，降低光谱信息冗余[3]。

高光谱的数据降维方法主要可分为维数约简和波段选择两大类。维数约简就是通过线性或非线性数学变换，将高维数据转化为可解的低维数据[4]。波段选择则是从多达数百个波段的高光谱影像中，选择具有较好分类识别能力的波段组合，代替原始全波段数据参与分析与应用[5]。

维数约简通常涉及数学运算，容易破坏数据原始光谱结构，不利于地物光谱信息提取，波段选择则不存在此问题。波段选择方法的研究成果很多，包括基于稀疏的波段选择[6](sparse based band selection，SpaBS)、稀疏矩阵分解的波段选择法[7](sparse nonnegative matrix factorization，SNMF)、自适应波段选择[8](adaptive band selection，ABS)、加权概率原型分析的高光谱影像波段选择[9]等。

不同于上述方法，本文提出一种相对熵结合互信息的光谱综合信息量分析波段选择(Kullback-Leibler divergence and mutual information based band selection，KLMIBS)方法来研究高光谱影像的波段选择问题。通过构建高光谱影像光谱信息的总体分布模型进行波段选择，并利用一个高光谱影像公开数据集进行实验与精度分析，验证本文提出的KLMIBS方法的有效性。

1 光谱信息分布模型

高光谱影像波段选择的结果中，除了要求不改变原始光谱数据结构，保持原始波段物理含义不变之外，还应该尽可能多地保留地物的有效光谱信息[10]。因此，需要对整幅影像的光谱信息总体分布情况进行分析与建模。KLMIBS方法选择相对熵(relative entropy，RE)[11]结合互信息[12](mutual information，MI)构建光谱信息总体分布的定量描述模型，指导高光谱影像的波段选择。

1.1 待选择的波段数量

研究波段选择问题，首先需要确定待选择的波段数量。高光谱影像处理算法通常要求选出的波段数量必须大于或等于端元数量[13]。端元数量可通过主成分分析[14](principal component analysis，PCA)、最小噪声分离[15](minimum noise fraction，MNF)、奇异值分解[16](singular value decomposition，SVD)、噪声子空间投影[17](noise subspace projection，NSP)和基于最小误差高光谱信号识别[18](hyperspectral signal identification by minimum error，HySime)等方法得到。

其中，HFC和NWHFC方法都是基于相关矩阵和协方差矩阵特征值之间的协方差趋近于0的假设条件，利用虚拟维度估计端元数量的。不同之处在于，NWHFC在执行HFC之前，对样本相关矩阵和样本协方差矩阵进行了噪声白化，去除了噪声方差的相关性，使得虚拟维度的估计更加精确。HFC和NWHFC的主要问题在于，估计的准确度比较一般，且样本数量不是很大时，其假设条件不成立。NSP仅采用白化后的样本协方差矩阵进行虚拟维数的估计，不受样本数量的影响。在噪声估计正确的前提下，尤其是样本个数不多时，该方法优于HFC和NWHFC。

对于高光谱遥感影像的端元数量估计问题，PCA丢弃的主分量中可能包含真实端元；HFC和NWHFC的假设条件受样本数量影响很大；NSP 则需要精确估计噪声和给定误警率。HySime尽管计算过程较复杂，但不需要任何参数且估计准确度较高，综合性能最优。因此，选择HySime算法估计高光谱影像的端元数量。

1.2 高光谱影像光谱差异信息模型

相对熵又称KL散度(Kullback-Leibler divergence)或信息散度(information divergence)，是2个概率分布P和Q差别的非对称性的度量，用来度量使用基于Q的编码来编码来自P的样本，平均所需的额外比特个数。为避免混淆，下文将相对熵、KL散度和信息散度统称为KL散度。

设P(x)和Q(x)是X取值的2个离散概率分布，则P对Q的KL散度为：

(1)

KL散度仅当概率P和Q各自总和均为1，且对于任何x都满足Q(x)>0及P(x)>0时，才有定义。

对于连续随机变量，其概率分布P和Q可按积分方式定义为式(2)：

(2)

式中：p和q分别表示分布P和Q的密度。

从式(1)和式(2)可以看出，KL散度总是非负，当且仅当分布P和Q完全相同时，KL散度为0；P和Q的相似度越高，KL散度越小；相似度越低，KL散度越大。可以将分布P和Q分别与高光谱图像中2个波段的光谱数据进行类比，则2波段数据的相似度越低，信息差异(即有效信息量)越大，则对应的KL散度数值越大，反之则越小。因此，选择利用KL散度参数描述波段间的有效光谱信息。

DKL(P‖Q)只能描述2个波段P和Q之间的光谱信息差异，而波段选择过程需要对高光谱影像全部波段间光谱信息差异的整体分布进行定量描述。因此，定义了一个KL散度矩阵MKL。对于高光谱数据X∈RN×M(R代表非负实数集，N是全部像元的数量，M是所有波段的数量)，MKL是一个M×M的方阵，如式(3)所示。

(3)

式中:Xi表示高光谱数据中所有像元在第i波段的数据；DKL(Xi‖Xj)表示所有像元从波段i到波段j的KL散度，可用公式(1)计算。

1.3 高光谱影像光谱冗余信息模型

为了更全面地描述光谱信息量整体分布情况，不仅需要建立有效光谱信息的整体分布模型，还需要对冗余光谱信息进行整体分布的定量化描述，建立光谱冗余信息的整体分布定量模型。为此，论文引入了信息学中的互信息MI(mutual information)参数。

互信息是用来度量随机变量之间独立性的基本准则，可以表示成KL散度的形式。多个随机变量之间的互信息定义为其联合概率密度函数与各边缘密度函数乘积之间的KL散度，即：

(4)

将式(4)右边继续展开：

(5)

由于KL散度的非负性可知：

(6)

互信息量I(ai；bj)在联合概率空间P(XY)中的统计平均值，称为平均互信息(average mutual information，AMI)，其计算公式如(7)所示。

(7)

利用平均互信息量是为了克服互信息量的随机性，使其成为一个确定的量。关于平均互信息量的物理意义，以I(X；Y)为例，即在对Y一无所知的情况下，X的先验不定度与收到Y后关于X的后验不确定度之差。可以用平均互信息量来定量表示谱间冗余信息，为波段选择提供依据。

基于上述分析，本文定义了一个平均互信息矩阵，记为MI，作为高光谱影像整体光谱冗余信息模型。MI是一个M行、M列的方阵，如式(8)所示。

(8)

式中:I(Xi；Xj)表示波段i和波段j之间所有像元反射率的平均互信息，该数值可依据式(7)进行计算。

1.4 高光谱影像光谱综合信息模型

为了更加全面地表述所有波段之间的光谱信息分布，同时抑制单参数的负面影响，算法将KL散度矩阵MKL和平均互信息量矩阵MI以不同的权重系数进行结合，生成一个综合光谱信息矩阵S，作为高光谱影像的整体光谱信息模型，并将其作为波段选择过程的主要参考。

通过对KL散度和平均互信息参数的综合，可以完整地反映光谱信息量的谱间相关特征。式(9)给出了图像中任意2个谱段数据X和Y之间的谱间相关模型。

S(X，Y)=DKL(P‖Q)-λ·MI(X；Y)

(9)

式中：S(X，Y)为波段X和波段Y之间的谱间相关性；DKL(P‖Q)为波段X的概率分布P和波段Y的概率分布Q之间的KL散度；MI(X；Y)为波段X和波段Y之间的平均互信息；λ为权重系数，由DKL(P‖Q)和MI(X；Y)的均值的相对幅度大小决定。

容易知道，与MKL和MI相同，S也是一个M行、M列的方阵，如式(10)所示。

(10)

S中较大的数值代表较大的光谱信息差异(也可以理解为有效光谱信息，区别于冗余光谱信息)和对应波段之间较小的光谱信息依赖程度(也可以理解为较小的光谱信息冗余)。S(i，j)表示波段i和波段j之间所有像元的综合光谱信息差异(或可以理解为有效光谱信息)。S(i，j)的计算如式(11)所示。

S(i，j)=cKLDKL(Xi‖Xj)-cIMI(Xi；Xj)

(11)

式中：cKL和cI分别对应KL散度矩阵MKL和平均互信息量矩阵MI的权重系数。由于KL散度和平均互信息量对于波段选择过程的参考意义基本上同等重要，为了使对应矩阵MKL和MI对于S的贡献度基本相当，需要参照归一化思想，对MKL和MI按照其内部元素的平均幅值的比例关系分别赋予相应权重。具体来说，即权重系数cKL和cI由MKL和MI中所有元素绝对值的均值的比值确定，如式(12)所示。

(12)

由于只关心cKL和cI之间的相对比值，而非二者的绝对数值，因此S的计算公式可以转换为式(13)。

(13)

1.5 KLMIBS处理流程

希望利用矩阵S同时选出全部待选波段是不切实际的。本文算法主要基于如下技术思路：每次仅从剩余波段中选择一个波段，该波段在所有待选波段中，包含了相对于已选择波段集合最多的有效光谱信息。

对于矩阵S中的随机一列：si={S(1，i)，S(2，i)，…，S(M，i)}，它代表波段i相对于其余全部波段的有效光谱信息(差异化光谱信息)。

S是MKL和MI的综合，S中较大数值的元素，意味着对应2个波段之间同时具有较大的KL散度值和较小的平均互信息，也就是说，对应2个波段之间的光谱信息差异较大，光谱信息冗余较小，这正是波段选择算法的理想依据。

KLMIBS波段选择方法流程如下：

①利用Hysime估计高光谱图像的端元数量，将端元数量估计结果确定为波段选择数量T。

②计算综合信息量矩阵S。基于式(1)和式(3)计算KL散度矩阵MKL，基于式(7)和式(8)计算平均互信息矩阵MI，基于式(12)和式(13)计算S。

③选择第一个波段。选择x1∈[1，M]，M为波段数量，使得sx1={S(1，x1)，…，S(M，x1)}在所有的si={S(1，i)，…，S(M，i)}，i=1，2，…，M中取最大值，则序号为x1的波段即为第一个被选择波段。

④依次选择剩余T-1个波段。假设全部已选择波段的序号集合为K={K1，…，KU}，其中U为已选波段数量，选择xi∈[1，M]，i∈[2，T]，xi∉K，计算SK=S(K1，xi)+…+S(KU，xi)，使得SK在所有的xi中取最大值，则xi即为第i个被选择波段序号。按照④中步骤依次选择剩余的T-1个波段，并将选中的每一个波段序号加入集合K，则最终生成的波段序号集合K即为算法的波段选择结果。

2 真实数据波段选择实验

真实实验数据为高光谱数据图像收集实验仪器(hyperspectral digital imagery collection experiment，HYDICE)在美国华盛顿特区采集到的高光谱数据集，如图1所示。该高光谱影像的行数与列数均为400。该数据原始波段数量210，波段范围0.4～2.4 μm，波段宽度为10 nm，涵盖了可见光和近红外谱段范围；在去除了0.9～1.4 μm范围内的大气吸收波段后，剩余191个有效波段。

图1 美国华盛顿特区HYDICE高光谱数据

根据KLMIBS波段选择方法流程，首先利用HySime方法得到该影像子区的端元数量估计值为10，确定待选择的波段数量为10。在191个有效波段中，KLMIBS最终选择的10个波段的下标集合如下：{5，13，26，39，47，56，71，82，136，191}。

图2给出了波段选择算法结果对应的综合光谱信息矩阵S的三维视图(图2(a))，以及10个选择波段的光谱三维视图(图2(b))。如图2(a)所示，图中峰谷起伏程度越大，代表各波段之间的光谱差异信息(有效信息)越多，光谱相关信息(冗余信息)越少；说明KLMIBS方法中的矩阵S能够将两两波段之间的光谱信息差异有效凸显出来，同时能够对所有波段之间的光谱有效信息整体分布情况进行定量描述。如图2(b)所示，10个选定波段的集合中各波段之间的光谱幅值差异十分显著，说明选出的波段集合包含的光谱信息冗余小，有效光谱信息量大。

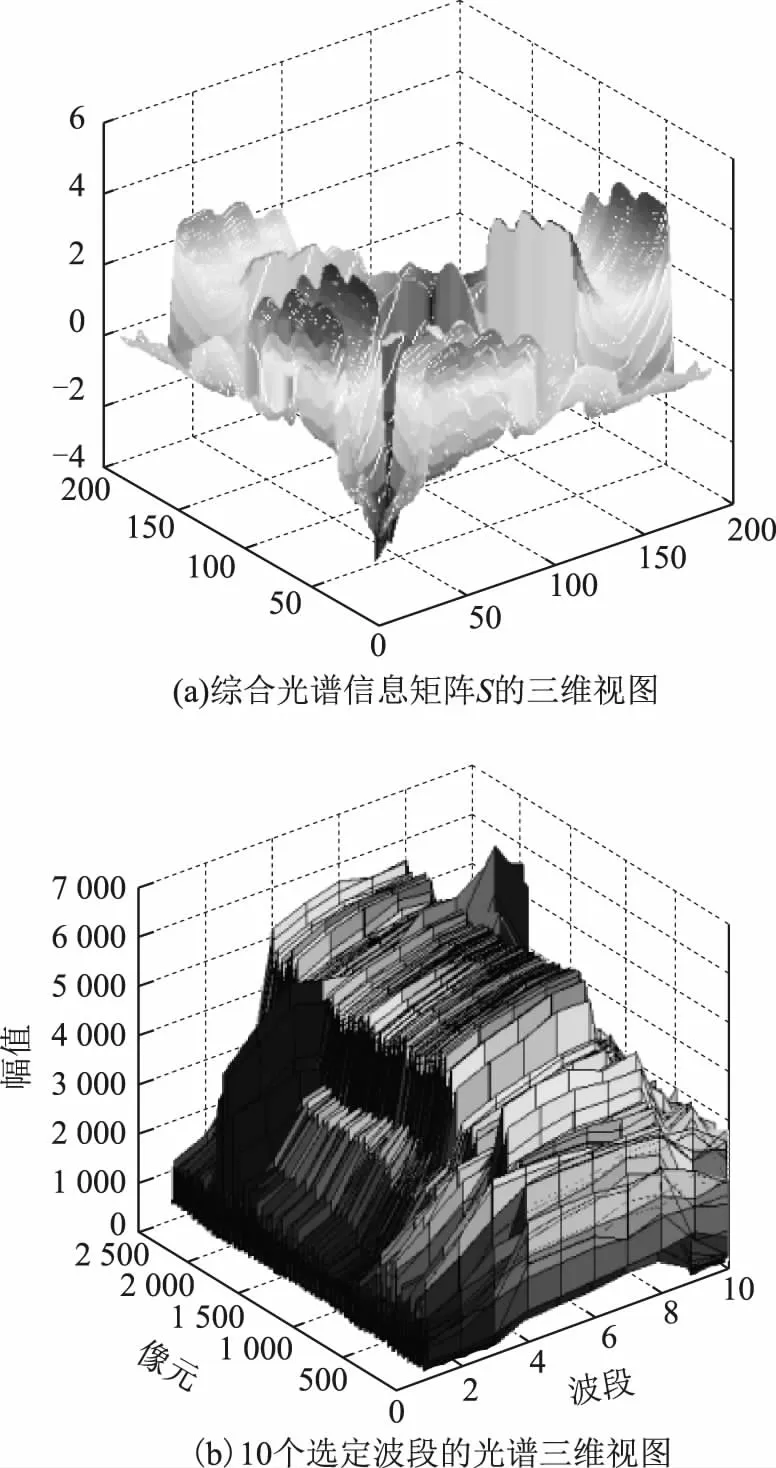
图2 KLMIBS波段选择实验结果

为进一步定量分析和验证KLMIBS方法的性能，将KLMIBS与前文所述的SpaBS、SNMF和ABS 3种代表性波段选择方法的波段选择结果在真实高光谱遥感图像中的像元解混精度进行对比。

像元解混算法统一采用最小体积约束的非负矩阵分解(minimum volume constrained NMF，MVCNMF)。MVCNMF是目前光谱解混研究中成果最多的基于凸面几何学理论的方法中很有代表性的一种，通过将体积限制加入到NMF中，将最小二乘分析和凸面几何结合起来，具有较高的解混精度。MVCNMF提出的代价函数包括两部分，一部分为估量观测数据与端元和丰度重建数据之间的近似误差，另一部分由最小体积限制组成。

利用MVCNMF的端元光谱估计值与地面实测真值之间的光谱夹角距离[13](spectral angle distance，SAD)作为解混结果的精度评价参数，单位为弧度。SAD越小，代表像元解混精度越高，解混效果越好。

KLMIBS与SpaBS、SNMF和ABS的波段选择结果的MVCNMF解混精度对比如表1所示。

表1 不同波段选择算法的MVCNMF解混精度

如表1所示，与其他3种方法相比，KLMIBS对应的SAD最小，代表其选择结果的MVCNMF解混精度最优，说明该方法能够很好地保留有效光谱信息，去除冗余光谱信息，波段选择效果优于多数同类算法。

3 结束语

论文研究结果表明，在波段选择过程中对高光谱影像进行光谱信息量分析，通过引入KL散度与(平均)互信息2种信息学参数，分别对波段间的光谱差异信息与光谱冗余信息进行建模，并生成反映整幅影像有效光谱信息整体分布情况的综合模型，能够在数量非常有限的波段集合中，相对于其余几种代表性波段选择方法保留更多的光谱有效信息，有助于后续高光谱影像分析与处理。

相对于前人在高光谱影像波段选择方面的研究成果，论文主要在以下两个方面进行了改进与创新：一是通过赋予不同权重系数，融合2种代表性信息学参数，对高光谱影像的有效光谱信息整体分布状况进行建模和定量描述；二是提出的KLMIBS方法属于非监督方法，能够显著降低对先验知识的依赖程度，相对于部分对先验知识依赖程度较高的波段选择方法，在一定程度上改善了实用性，在后续处理中，其波段选择结果也具有令人满意的精度。

在今后工作中，该方法的适用范围与稳定性还需进一步分析与验证；基于KLMIBS的技术思路，其他信息学或统计学参数组合，以及其他权重系数计算方法，也都值得进一步尝试与检验。