调速系统参数对异步联网系统暂态频率稳定性的影响

陈春敏，孙士云，安德超，孙德娟，海世芳

（1.中国能源建设集团云南省电力设计院有限公司，昆明 650051；2. 昆明理工大学 电力工程学院，昆明 650500）

0 前言

在电网中大容量机组所占的比例越来越大，引起低频振荡、频率不稳定现象时常发生，当频率出现不稳定时，会引起潮流、电压等状态变量的波动，对系统稳定性不利。为了控制系统频率的波动在允许范围内，机组的调速系统起到了关键作用，特别是调速系统的参数。目前，大量的工作主要集中在机组调频参数的辨识，同时机组调频参数对系统频率的影响也开展了一些研究。文献[1-2]基于发电机组调频机理，建立了机组并网运行的一次调频数学模型，理论分析了调差系数、调频容量、调速器死区参数设置对电网频率存在的影响。根据实际的电网仿真，验证了一次调频参数设置对电网频率有较大影响，同时一次调频容量大，频率的波动的最大值、稳态频率偏差都减小。

文献[3]对燃煤机组及燃气轮机施加转速阶跃试验，分析研究其动态特性，提出了一种新的原动机及调速器模型。在转速阶跃试验的实测数据基础上，结合响应特性模型和优化算法进行参数辨识。采用新的原动机及调速器模型重现频率扰动试验，仿真数值和实测值较接近，证实了该模型的合理性。

文献[4] 基于单元机组协调控制系统CCS的原理，以及相关环节的简化，建立了适用于电力系统稳定计算的CCS 的简化模型。新汽轮机调速器模型由现有的汽轮机数字电液控制系统DEH 模型及主汽压力的原有模型构成。文献[5]提出了适当简化的汽轮机及调速系统的数学模型，频域、时域仿真表明，调速系统参数的改变对系统的影响存在差异，系统阻尼可能为正，也可能为负。对于调速系统复杂系统阻尼特性的分析，所提出模型适用能力强，且计算精度高。

文献[6]提出了非线性、线性的水轮机模型。WECC 测试比较了水轮机机组实际出力和仿真结果，验证原动机及调速器模型的准确性。但是现有仿真频率不能真实反映实际系统的情况，存在较大偏差，同时提出了GGOV1 模型[7-8]。随后，WECC 改进了传统的水轮机及调速器模型，提出了能准确计算分析系统中、长期稳定的水轮机模型[9]。

文献[10,11]以某实际电网为研究对象，分析了水电机组调速系统调速特性以及水电机组调速系统对独立电网频率稳定性存在的影响，得出微网中水电机组安全自动装置动作受其调速系统的影响，水电机组调速系统对小电网频率的影响受不同水轮机的容量影响而发生变化，同时水电机组调速系统之间的配合对独立电网频率影响受不同机组容量的不同而不同。文献[12]介绍了水轮机的3 种线性模型及3 种非线性模型，电力系统的暂态分析计算受水轮机模型影响，采用不同的水轮机模型分析计算，得到的结果不一致。同时，对比分析了稳定分析结果和适用范围两方面。

文献[13] 分析了2 机系统频率动态过程的原理，通过时域仿真分析了发电机惯性时间常数、调速器及其参数变化对复杂拓展多机系统频率动态过程的影响。仿真结果表明，死区明显的抑制了系统频率下降的深度，死区越小，频率下降得越慢，且下降的数值越小；频率第二摆的峰峰值和频率稳态值均受调差系数的影响。发电机惯性时间常数明显的抑制了频率的下降速度，惯性时间常数越大，频率下降速度慢。

为了满足系统的正常运行，频率必须维持在额定值附近，偏移量不超过规定值。频率的维持和控制是保证电能质量的必要条件，调速器的功能是在电网频率发生变化或者AGC 指令改变时，调节原动机的输入，使发电机的有功和负荷达到平衡的，最终维持频率的稳定。因此，机组的调速系统参数对异步联网系统频率稳定的维持起到了重要作用。

截止2016 年底， 云南电网装机容量83639 MW，其中水力发电61631 MW，占总装机容量的73.7%，而大、中型水电机组的装机容量占水电总装机容量的绝大部分。结合云南电网的电源绝大部分为大、中型水轮机组的装机特点，分析水轮机调速系统对系统暂态频率稳定性的影响，并阐述调速系统的调差系数、调速器响应时间、软反馈时间以及水锤效应时间等参数与水轮机组调频能力关系。以3 机9节点系统和异步联网系统为例，仿真验证了水轮机组调速系统参数对异步联网系统暂态频率存在影响。

1 水轮机调速系统参数

1.1 调差系数

发电机的单位调节功率标志了随频率的升降发电机组发出功率减少或增加的多寡。机组的调差系数en和发电机的单位调节功率KG互为倒数。机组的调差系数en满足式（1）所示。

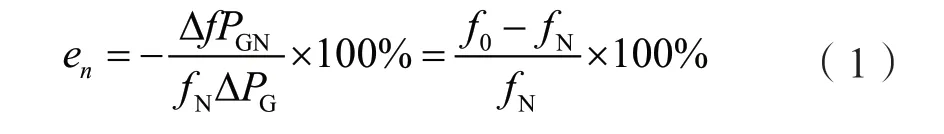
式中，PGN为发电组的额定功率，ΔPG为发电机组发出功率的增加或者减少量；fN为发电机的额定频率，Δf为发电机组的频率变化量。

由式（1）和式（2）可知，电网的频率稳定性受电网中各机组的调差系数的大小影响。电网中各机组的调差系数越大，即机组的单位调节系数越小，调频能力越小，频率偏移量较大，但系统的频率稳定性较好。反之，调差系数越小，即机组的单位调节系数越大，频率偏移量越小，但电网的稳定性较差。

系统中有多台发电机并联运行时，第i台发电机的调节方程按式（3）计算：

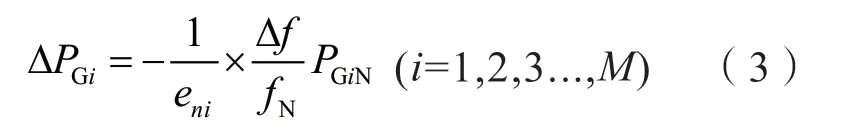
式中，PGiN为第i 台发电组的额定功率，ΔPGi为第i 台发电机组发出功率的增加或者减少量；eni为第i 台发电组的调差系数。

对式（3）求总和，并考虑到稳态时整个系统内频率的变化Δf是相同的，则式（4）成立：

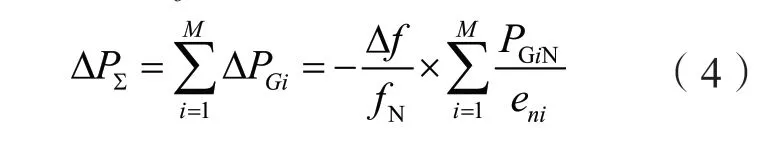
若用一台等值机组来代替时，则有：

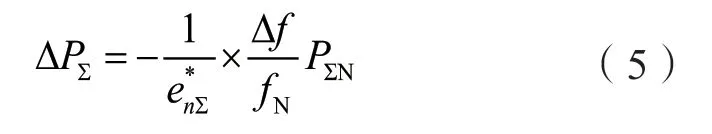
式中，ΔPΣ为全系统总的功率偏移量；PΣN为全系统总额度容量；为系统等值机组的调差系数。

由公式（3）可知，对于任意一台单独的大容量机组，其机组的调差系数小所承担的负荷增量要大，机组的调差系数大所承担的负荷增量要小。由公式（5）可知，对于全系统而言，系统中的并联运行的各机组的调差系数越小时，系统中一次调频能力就越大；系统中的并联运行的各机组的调差系数越大时，系统中一次调频能力就越小。

1.2 调速器响应时间

调速器一般由测量、积分放大、执行等环节构成。当系统的频率发生微小的变化时，调速器要经过测量、放大、执行等环节而带有一定的时延后响应。因此调速器的响应时间取决于各环节的响应时间，各环节响应时间越短，对系统频率的调节响应越快，频率不会出现大幅的波动；反之，各环节的响应时间越长，对系统频率的调节响应越慢，系统频率的波动性增强。

1.3 软反馈时间

软反馈只在瞬态中起作用，稳态时消失，因此把软反馈称为暂态反馈，反馈量的大小只与输入信号的变化率成正比。为了使调节系统稳定和改善动态品质，设置了暂态反馈环节。暂态反馈环节位于主接力器和引导阀之间。缓冲器是暂态反馈环节中起软反馈作用的校正环节，它的性能直接影响着调速器工作过程的稳定性和动态品质。

暂态反馈的结果，削弱了第二级放大环节的输入信号，实现了负反馈。加入暂态反馈后，使主配压阀回复到中间位置，使调节系统稳定，这是有利的一面；但由于反馈作用，使主配压阀油孔开度较无反馈时小，因此，主接力器的位移速度要减慢，机组的最大转速升高值会加大，对系统的稳定不利。

软反馈效应时间取决于暂态反馈时间和主接力器响应时间的大小，通常忽虑暂态反馈时间，只靠考虑主接力器响应时间。而主接力器响应时间按式（6）计算。

式中，An为接力器活塞有效面积；Kq为流量增益。

对于滑阀来说，流量增益是随着输入u的改变而变化的，其计算按式（7）计算。

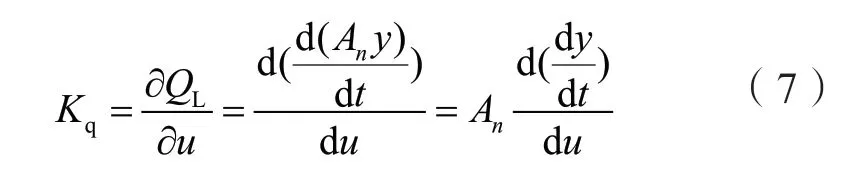
式中，u为配压阀阀心位移控制量；y为输出液压缸（主接力器）位移，QL为水流流量。

在实际应用中，将接力器响应时间定义为接力器带规定负载，其速度与配压阀相对行程u关系曲线徐率的倒数。即：

由于Kq随着u的改变而改变，使得接力器响应时间Ty在调节过程中不能保持恒定值，对调节系统的性能产生影响。

1.4 水锤效应时间

水锤效应是由压力管道中的水流惯性所引起的。在压力管道中的水在稳态情况下，水的流速是一定的，但当迅速关小导向叶片的开度时，导管中的压力降急剧上升，而当迅速开大导向叶片的开度时，导管中的压力降急剧下降，称之为水锤效应。

在小波动范围内，水体及管道基本上可以认为是刚性的。可以用刚性水击理论来描述压力引水系统的动态特性。由力学可知，刚性水击时压力变化为：

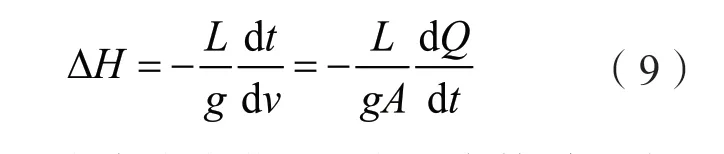
式中，ΔH为水头变化；L为引水管道长度；v为水流速度；A为管道横截面积；Q为水流流量。

有拉氏变化得到刚性水锤压力引水系统传递函数为：

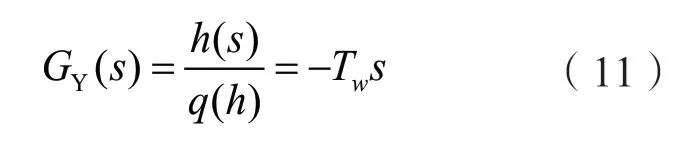
其物理意义表示，压力引水系统中的水流在不变水头Hr的作用下，若不考虑管道内水力损失，流量从0 增大到Qr所需的时间。它表征引系统中水流惯性的重要参数，在其他条件相同时，Tw的值越大，水锤压力值越大，对调节过程的影响也越大。使得水轮机功率不能跟随开度的变化而有一个滞延。因此水锤效应滞延的时间越大，功率的变化越大，导致系统频率的偏移也越大；反之，水锤效应滞延的时间越小，功率的改变量越小，系统频率的偏移也越小。

2 水轮机调速系统仿真模型

为了满足云南电网的大、中型水电机组的电源特性，选取BPA 中的水轮机调速器和原动机模型（GH）作为水轮机组的调速系统模型，该模型适用于大、中型水电机组。GH 模型框图如图1 所示。图中，PMAX为最大原动机输出功率（MW）；en为调差系数；TG为调速器响应时间；TP为引导阀门时间常数；Ty为软反馈时间常数；TW/2 为水锤效应时间常数；VELCLOSE为最大水门关闭速度，每秒标么。标么值为正数，且等于一个单位PMAX，必为正数；VELOPEN为最大水门开启速度，每秒标么；Dy为软反馈环节系数；ε 为死区，相对于系统频率的标么值；H 是总的水头。其中，PMAX标么值＝PMAX/功率基准值；K’ ＝PMAX( 标么)；Tw=2*Tw/2；PUP＝(VELOPEN)(PMAX标 么 值）；PDOWN=(-VELCLOSE)(PMAX标么值）。

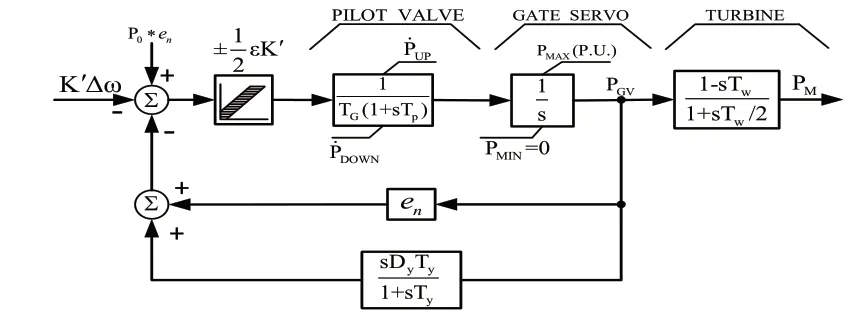
图1 GH模型

GH 模型的主要参数典型值取值范围如表1所示：

表1 GH模型的主要参数典型值取值范围

3 实际系统仿真验证

对云南电网的昆明、昭通、曲靖、红河、文山、玉溪、普洱、景洪、博尚、德宏地区的所有水轮机调速器-原动机模型中的调差系数、调速器响应时间、软反馈时间、水锤效应时间进行修改，并对比分析修改参数值、原参数值在直流线路发生直流故障和交流N-2 故障时，对云南电网频率的影响。调速系统4 种参数设置如表2 所示。

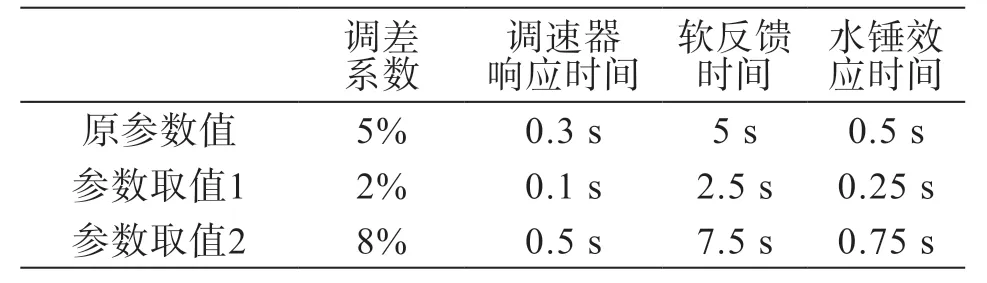
表2 调速系统4种参数设置

3.1 直流故障

在正常运行状态下，±500 kV 鲁西背靠背直流双极向外输送电功率达到2000 MW，单极输送功率能力为1000 MW。鲁西背靠背直流的正、负极直流输电线路在10 周波发生双极极直流闭锁故障，损失功率2000 MW。分析水轮机调速器-原动机模型中的调差系数、调速器响应时间常数、软反馈时间常数、水锤效应时间常数进行修改对电网频率的影响。

3.1.1 调差系数对频率稳定性的影响

机组调速系统的调差系数按表2 中的取值进行修改，仿真分析不同调差系数取值下系统母线频率的变化趋势，500 kV 圭山、墨江母线的频率特性曲线如图2 所示。

由图2 中的图a）、b）可知，调差系数按照2%、5%、8% 从小到大的顺序排列时，圭山母线对应的最大频率峰值偏移值分别为0.436 Hz、0.443 Hz、0.449 Hz；墨 江 母 线 对应的最大频率峰值偏移值分别为0.438 Hz、0.443 Hz、0.449 Hz。

由图2 中可以看出，在频率上升动态过程的初始阶段，调差系数的改变对频率基本没有影响。调差系数越大，频率上升幅度较大，调速系统调出的有功较少，但频率下降的幅度相对较小，且系统的稳定性较好。调差系数较小时，对应的频率跌落值较大，且频率跌落到最低点的时间较短，系统频率快速稳定性差。

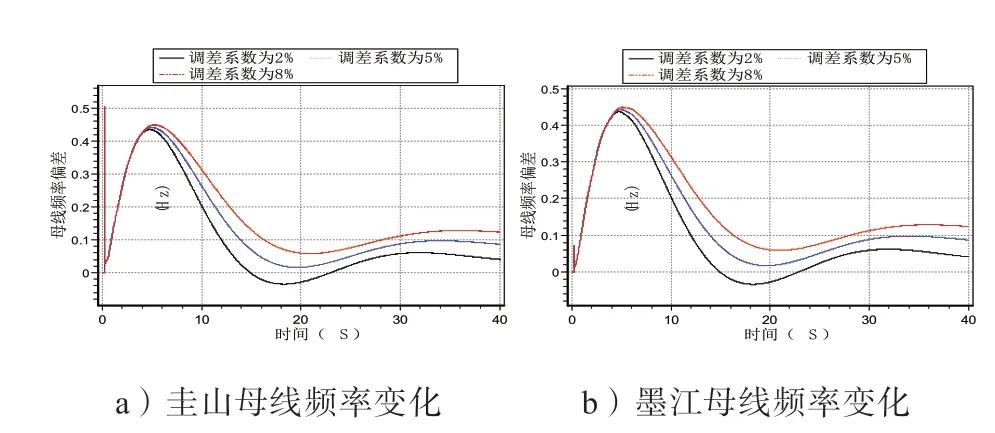
图2 改变调差系数时母线的频率曲线

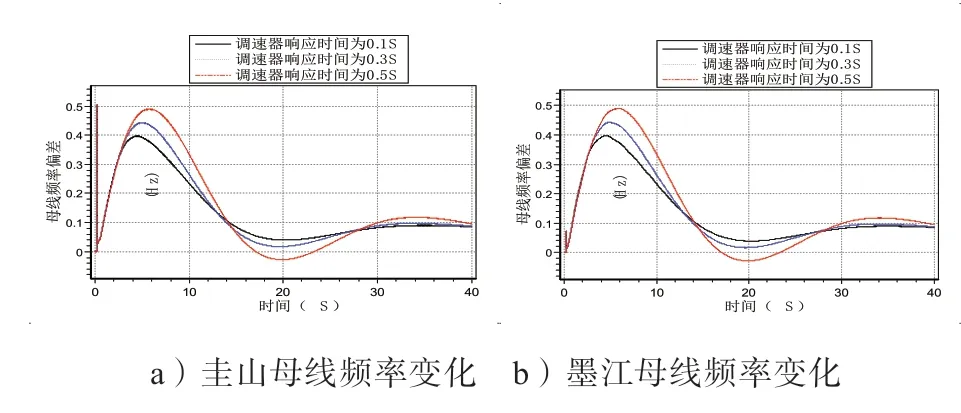
图3 改变调速器响应时间时母线的频率曲线

3.1.2 调速器响应时间对频率稳定性的影响

机组调速系统的调速器响应时间按表2 中的取值进行修改，仿真分析不同调速器响应时间取值下系统母线频率的变化趋势，500 kV 圭山、墨江母线的频率特性曲线如图3 所示。

由图3 中的图a）、b）可知，调速器响应时间0.1 s、0.3 s、0.5 s 从小到大的顺序排列时，圭山母线对应的最大频率峰值偏移值分别为0.397 Hz、0.442 Hz、0.489 Hz；墨 江 母 线对应的最大频率峰值偏移值分别为0.397 Hz、0.444 Hz、0.491 Hz。

由图3 中可以看出，在频率上升的初始阶段，改变调速器响应时间对频率的响应基本无影响。调速器响应时间越大，频率上升幅度越大，且频率上升到波峰或者下降到波谷的时间较长，频率的偏移值最大。调速器响应时间越小，频率上升值减小，且频率上升或下降的幅度较小，系统频率的快速稳定性好。

3.1.3 软反馈时间对频率稳定性的影响

机组调速系统的软反馈时间按表2 中的取值进行修改，仿真分析不同软反馈时间取值下系统母线频率的变化趋势，500 kV 草铺、黄坪母线的频率特性曲线如图4 所示。

由图4 中的图a）、b）可知，软反馈时间按照2.5 s、5 s、7.5 s 从小到大的顺序排列时，草铺母线对应的最大频率峰值偏移值分别为0.439 Hz、0.441 Hz、0.444 Hz；黄 坪 母 线对应的最大频率峰值偏移值分别为0.439 Hz、0.443 Hz、0.444 Hz。

由图4 中可以看出，在频率上升的初期，取不同的软反馈时间对频率影响很小。软反馈时间越大，频率上升幅值越大，且频率上升到波峰或者下降到波谷的时间延迟。软反馈时间减小，频率上升值减小，频率下降到最低点时间缩短，频率下降速度最快，但频率波动范围较大，且偏差值最大。

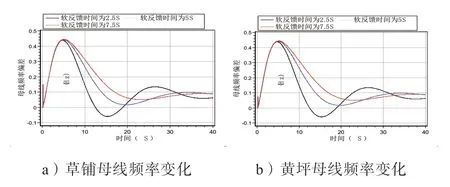
图4 改变软反馈时间时母线的频率曲线

3.1.4 水锤效应时间对频率稳定性的影响

机组调速系统的水锤效应时间按表2 中的取值进行修改，仿真分析不同水锤效应时间取值下系统母线频率的变化趋势，500 kV 草铺、黄坪母线的频率特性曲线如图5 所示。

由图5 中的图a）、b）可知，水锤效应时间按照0.25 s、0.5 s、0.75 s 从小到大的顺序排列时，草铺母线对应的最大频率峰值偏移值分别为0.387 Hz、0.443 Hz、0.507 Hz；黄坪母线对应的最大频率峰值偏移值分别为0.386 Hz、0.442 Hz、0.509 Hz。

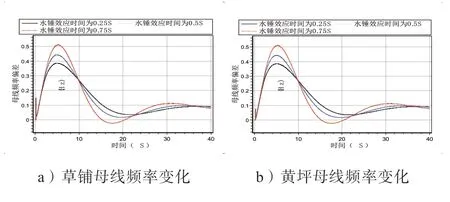
图5 改变水锤效应时间时母线的频率曲线

由图5 中可以看出，水锤效应时间对系统频率的影响，与调速器响应时间对频率稳定影响规律类似，因此不再概述。

3.2 交流故障

漫湾- 草铺500 kV 交流输电线路发生N-2故障时，漫湾电厂送电通道被切断，系统出现1616 MW 功率缺额，分析水轮机调速器-原动机模型中的调差系数、调速器响应时间常数、软反馈时间常数、水锤效应时间常数进行修改对电网频率的影响。

3.2.1 调差系数对频率稳定性的影响

机组调速系统的调差系数按表2 中的取值进行修改，仿真分析不同调差系数取值下系统母线频率的变化趋势，500 kV 红河、惠历母线的频率特性曲线如图6 所示。

由 图6 中 的 图a）、b） 可 知， 调 差 系数按照2%、5%、8% 从小到大的顺序排列时，红河母线对应的频率偏移最大峰值分别为-0.447 Hz、-0.459 Hz、-0.474 Hz；惠 历 母线对应的频率偏移最大峰值分别为-0.447 Hz、-0.459 Hz、-0.474 Hz。

由图6 中可以看出，在频率下降动态过程的初始阶段，调差系数的改变对频率基本没有影响。调差系数越大，频率下降幅度越大，调速系统调出的有功较少，但频率回升的幅度相对较小，且系统的稳定性较好。调差系数较小时，对应的频率跌落值减小，且频率跌落到最低点的时间较短，能有效控制频率的跌落，但系统的频率快速稳定性差。

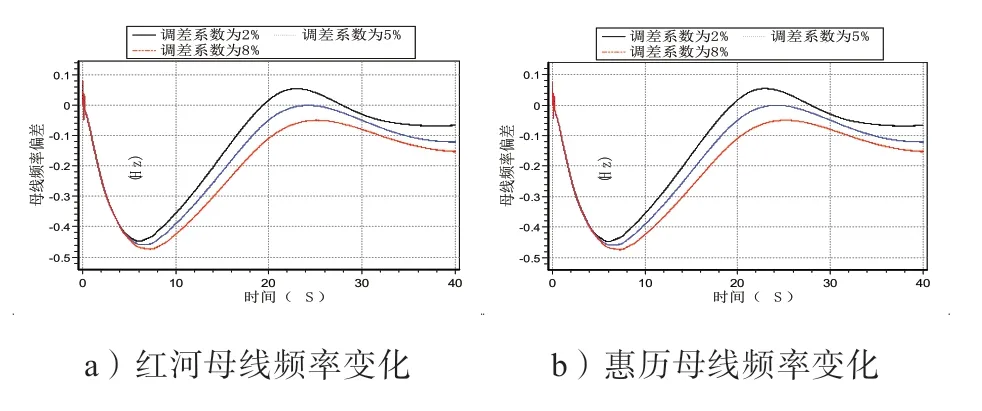
图6 改变调差系数时母线的频率曲线

3.2.2 调速器响应时间对频率稳定性的影响

机组调速系统的调速器响应时间按表2 中的取值进行修改，仿真分析不同调速器响应时间取值下系统母线频率的变化趋势，500 kV 红河、惠历母线的频率特性曲线如图7 所示。

由图7 中的图a）、b）可知，调速器响应时间按照0.1 s、0.3 s、0.5 s 从小到大的顺序排列时，红河母线对应的频率偏移最大峰值分别为-0.418 Hz、-0.458 Hz、-0.508 Hz；惠 历 母线对应的频率偏移最大峰值分别为-0.418 Hz、-0.458 Hz、-0.508 Hz。

由图7 中可以看出，在频率下降的初始阶段，改变调速器响应时间对频率的响应基本无影响。调速器响应时间越大，频率下跌幅度越大，且频率下降到波谷或者上升到波峰的时间较长，频率的偏移值最大。调速器响应时间越小，频率跌落值减小，且频率下降或上升的幅度较小，系统频率的快速稳定性好。

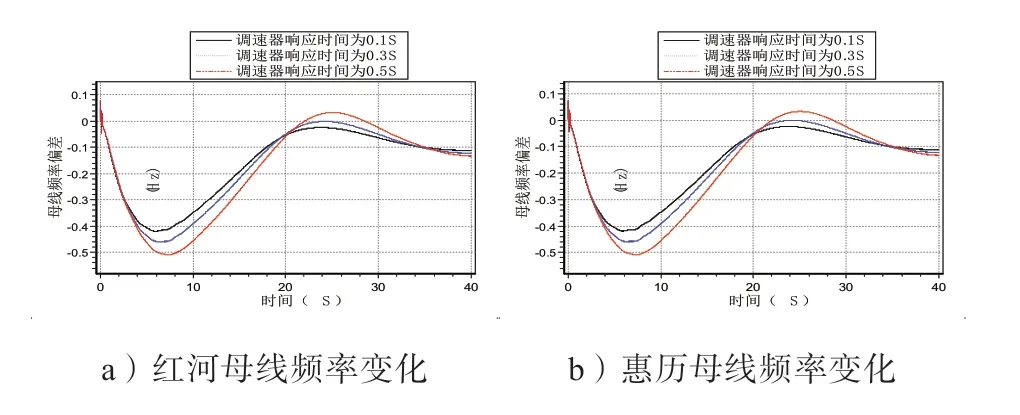
图7 改变调速器响应时间时母线的频率曲线

3.2.3 软反馈时间对频率稳定性的影响

机组调速系统的软反馈时间按表2 中的取值进行修改，仿真分析不同软反馈时间取值下系统母线频率的变化趋势，500 kV 红河、惠历母线的频率特性曲线如图8 所示。

由图8 中的图a）、b）可知，软反馈时间2.5 s、5 s、7.5 s 从小到大的顺序排列时，红河母线对应的频率偏移最大峰值分别为-0.446 Hz、-0.458 Hz、-0.468 Hz；惠历母线对应的频率偏移最大峰值分别为-0.445 Hz、-0.458 Hz、-0.468 Hz。

由图8 中可以看出，在频率下降的初期，取不同的软反馈时间对频率影响很小。软反馈时间越大，频率下降幅值越大，且频率下降到波谷或者上升到波峰的时间延迟。软反馈时间减小，频率跌落值减小，频率下降到最低点时间缩短，频率回升速度最快。频率再次下降的速度最快，频率偏差值最大。

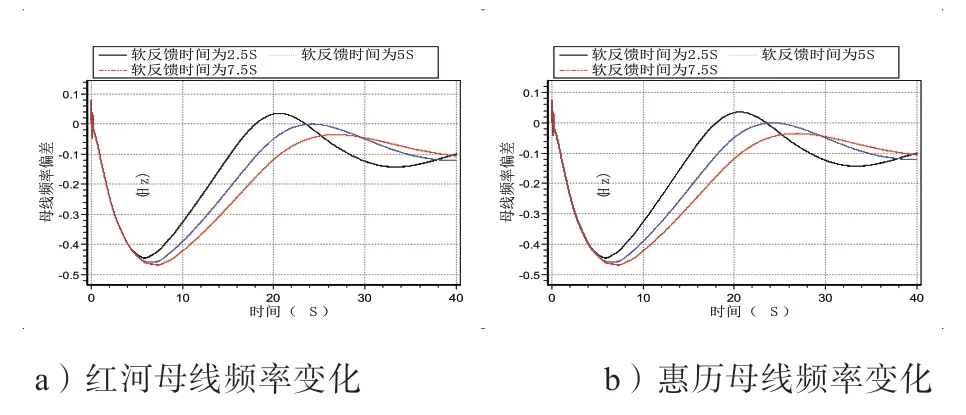
图8 改变软反馈时间时母线的频率曲线

3.2.4 水锤效应时间对频率稳定性的影响

机组调速系统的水锤效应时间按表2 中的取值进行修改，仿真分析不同水锤效应时间取值下系统母线频率的变化趋势，500 kV 红河、惠历母线的频率特性曲线如图9 所示。

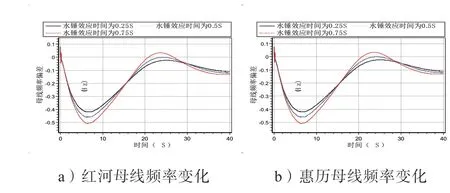
图9 改变水锤效应时间时母线的频率曲线

由图9 中的图a）、b）可知，水锤效应时间按照0.25 s、0.5 s、0.75 s 从小到大的顺序排列时，红河母线对应的频率偏移最大峰值分别为-0.416 Hz、-0.458 Hz、-0.506 Hz；惠 历 母线对应的频率偏移最大峰值分别为-0.418 Hz、-0.459 Hz、-0.506 Hz。

由图9 中可以看出，水锤效应时间对系统频率的影响，与调速器响应时间对频率稳定影响规律类似，因此不再概述。

4 结束语

通过分析水轮机调速系统参数对异步联网系统暂态频率稳定性的影响，得到相关的结论如下：

1）调差系数。在频率变化的初始阶段，调差系数的改变对频率基本没有影响。调差系数越大，频率变化幅度越大，调速系统调出的有功较少，但频率恢复稳态时频率偏差相对较小，且系统的稳定性较好。调差系数较小时，对应的频率跌落值减小，且频率跌落到最低点的时间较短，能有效控制频率的跌落，但系统的频率快速稳定性差。调差系数为2%的频率偏移最大峰值较小，但需要较长的时间系统频率才能趋于稳定，而调差系数为8%的频率偏移最大峰值较调差系数为2%的大，并系统稳定的快速性好。

2）调速器响应时间。在频率变化的初始阶段，改变调速器响应时间对频率的响应基本无影响。调速器响应时间越大，频率变化幅度越大，且频率到达波峰或者波谷的时间较长，频率的偏移值最大。调速器响应时间越小，频率变化值减小，且频率变化的幅度较小，系统频率的快速稳定性好。水锤效应时间对系统频率的影响，与调速器响应时间对频率稳定影响规律类似。

3）软反馈时间。在频率变化的初始阶段，取不同的软反馈时间对频率影响很小。软反馈时间越大，频率变化幅值越大，且频率到达波谷或者波峰的时间延迟。软反馈时间减小，频率跌落值减小，频率到达最低点时间缩短，频率恢复过程较快。