考虑调速器的电网PSS2B参数优化研究

闫飞

（中国能源建设集团安徽省电力设计院有限公司，安徽 合肥 230601）

0 前言

大规模直流输电技术快速发展，系统网络结构和运行方式发生变化，整体惯量减少，特别是对高压直流输电附近的输变电站的影响更为严重[1-2]。发电厂有功输出受到低频振荡的影响，严重的情况曾导致局部电厂发生功角失稳进而发生机组解列现象[3-4]。电力系统稳定器(PSS)通过附加在励磁系统前端为系统提供纯正阻尼，在提高系统的动态稳定性方面效果明显[5]。但是，目前大部分研究针对的都是汽轮机组的PSS2B 参数研究，并不能很好的实际电网情况。广西恭县某水电站曾因水轮发电机输出功率达400 MW 时，发生发散性振荡，致使机组无法投入使用。最后在励磁系统中加入PSS 后消除了振荡，使机组得以正常工作[6]。

目前，PSS 参数优化协调方面有诸多研究，近年来大部分PSS 参数协调研究集中在优化算法方面。较为主流的优化算法有遗传算法、粒子群算法、差分算法、免疫算法和进化规则，都在PSS 参数优化方面有所运用[7-10]，并且得到一些比较理想的优化效果。文献[11] 采用了免疫遗传算法，并结合系统机电模式的最小阻尼为目标函数来优化PSS 参数。文献[9] 提出了多机PSS 参数优化的新方法，目标函数设置为所有机电振荡模态性能的方程，将PSS 参数优化规划为带有不等式约束的非光滑优化问题，采用进化策略优化算法进行参数优化。文献[12-13]在合理配置PSS 的参数后，得到了理想的系统动态性能，提高了系统的稳定性。生物地理学算法(BBO)是基于物种迁移规律和突变现象建立的新型仿生优化算法[14]。与其它智能优化算法一样，标准BBO 算法也存在容易陷入局部最优的不足[15]。随着进化次数的不断增加，种群内个体的差异和多样性呈现逐渐减少的趋势，将会导致种群个体出现趋同现象，从而导致算法出现“早熟”现象。

为了优化出的PSS2B 参数能适应于电网的多种运行方式。因此，本文考虑了水轮机组对PSS2B 的影响，对电网实际采用的自并励励磁系统、调速器和PSS2B 进行了合理简化和线性化，并建立了符合电网实际情况的多机线性化模型。本文提出了自适应迁移操作和DE 变异操作改进标准BBO 算法进而获得改进后的BBO算法(BBO-DE)。最后，在PSASP 中搭建了电网部分区域电网模型，通过仿真验证了本文优化出的PSS2B 参数可以有效提高系统抑制低频振荡的能力，并能很好的适应于电网的多种运行方式。

1 多机系统线性化模型

本文研究主要针对，部分区域电网出现的低频振荡现象。现有电网中绝大部分发电机组采用的是自并励励磁系统、水轮机组调速器和PSS2B。对应PSASP 仿真软件中的型号分别为励磁模型12 型、调速器1 型和PSS 模型4 型。为了使建立模型能相对准确，本文考虑了水轮机组可能给系统带来新的振荡模式的影响和给PSS2B 参数优化带来的影响，在实际电网运行数据的基础上，对电网所采用的励磁系统、调速器和PSS2B 控制器进行了合理简化和线性化，建立了符合电网实际情况的多机系统线性化模型。

1.1 励磁系统线性化

自并励励磁系统传递框图如图1 所示，励磁调节器带有低励和过励限制两个环节，可由用户根据需要自行接入。而且PSS 输入信号可以选择在并联校正前接入，也可以选择在串联前接入。图中，Xc为调差阻抗，Kc为与换相电抗相关的整流器负荷系数，Tt1、Tt2、Tt3、Tt4、K为串联校正环节时间常数和增益，Tr测量环节时间常数，Ka、Ta分别为放大环节增益和时间常数，Kf、Tf分别为并联校正环节增益和时间常数，Kv为校正选择因子，Kv=1 时为比例积分型校正，Kv=0 时为纯积分型校正，Urmin、Urmax分别为调节器输出上、下限值，Uamin、Uamax分别为放大环节输出上、下限值，TL1、TL2和KL分别为过励限制环节时间常数和增益，TH1、TH2和KH分别为低励限制环节时间常数和增益。

图1 自并励励磁传递框图

目前电网采用的自并励励磁系统在正常运行时，都没有接入过励限制环和低励限制环节节，并且采用的是串联校正环节，即Kf=0。根据运行数据对自并励励磁系统参数进行分析时，发现大部分励磁系统的补偿环节时间常数为Tt3=Tt4，且调差阻抗Xc=0。根据实际电网情况，可将励磁系统进行合理简化，如图2 所示。图中，UT、UT1为2 个中间变量，其数学模型为：

图2 简化自并励励磁传递框图

式中，s为微分算子为励磁电压参考值。令dUpss/dt=UP_s，将式(1) 进行线性化处理可得：

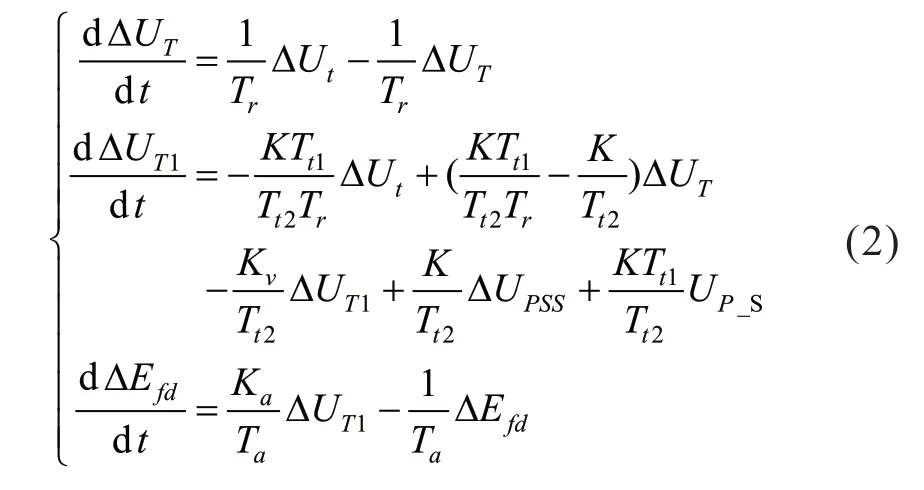
1.2 水轮机组调速器线性化

水轮机组机械功率相对容易变化，与系统并联的水轮机组，会给系统带来两个振荡模式，分别为与机电模式相近的水击模式和与水轮机调速器相关的机水模式[6]。电网大部分采用的都是PSS2B 模型，但是由于PSS2B 模型中含有合成机械功率Pm通道，在针对电网实际情况研究低频振荡时，不能在忽略调速器的影响。只有考虑水轮机调速器的影响，才能优化得到更好的PSS2B 参数。电网绝大部分采用的调速器传递框图如图3 所示。图3 中，Kδ为量测环节增益，Ts为伺服机构的时间常数，Tω为水锤效应时间常数，Ka硬反馈环节增益，Ti和Kβ为软反馈环节时间常数和增益。Ur1、Ur2为状态过渡变量。

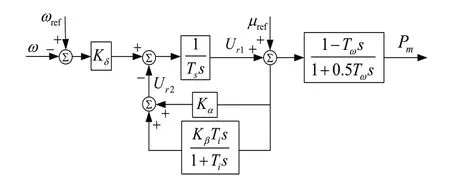
图3 电网水轮机组调速器传递框图

由图3 可得：

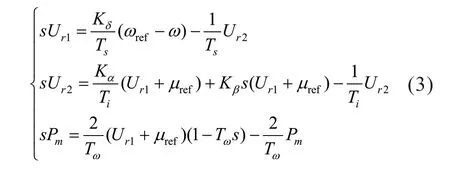
将式(3)进行线性化处理，可得

1.3 电网中的PSS2B线性化

目前对PSS2B 参数优化中，基本都是针对汽轮机组研究的，很少有论文专门讨论PSS2B的合成机械功率增量和考虑水轮机调速器给系统带来的振荡模式。本文提出了考虑PSS2B 中的合成机械功率通道和水轮机组调速器影响的建模。这样能使得本文的建模更加符合电网的实际情况。目前电网普遍采用的PSS2B 传递函数框图如图4。

图 4 电网PSS2B模型

图4 中，Trw和Kw分别为转速偏差时间常数和增益，T5、T6、T7为转速隔直环节时间常数，Kr、Ks分别为功率偏差增益和补偿系数，Tw、Tw1、Tw2为功率隔直环节时间常数，Tpω为功率测量时间常数，T9、T10、T12为陷波器环节时间常数，Kp为PSS 比例放大倍数，T1、T2、T3、T4、T13、T14为补偿环节时间常数。

图4 中的功率信号Pe和转速信号w 分别通过各自通道后得到功率偏差DPe和转速偏差Dw。两个信号合成机械偏差DPm原理如下：

将式(5)进行拉普拉斯变换，整理可得

根据传递框图4 和式(6)，消去不可测量的机械功率偏差ΔPm，可得：

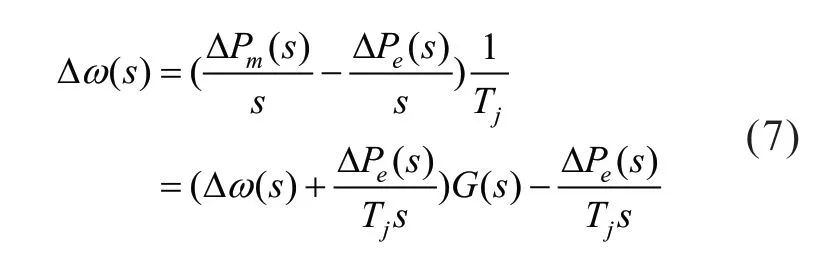
式中，G(s)为陷波器环节传递函数，见图4。

图4 中的隔直环节主要用于隔离稳态时的直流信号和一些频率特别低的信号。电网中绝大部分的隔离环节时间常数介于4～6 s 之间。此范围内隔离环节的交接频率为0.03～0.04 Hz，远远小于低频振荡的频率范围。结合电网的实际情况，在低频振荡研究范围内，可以对PSS2B 隔直环节进行合理简化。由于陷波器是一种高频滤波环节，在线性化处理时可忽略不计。本文考虑了调速器影响，提出一种考虑调速器影响的PSS2B 简化模型，如图5 所示。图中US1～US4、UPSS为过渡变量。

图5 PSS2B简化模型

根据图5 中PSS2B 的简化模型，整理可得：

将式(8)进行线性化处理可得：

1.4 电网部分等值法

物理等值法一般运用于系统规模较大且低电压等级网络较多的情况。不过，当仿真模型受到限制时，也可对系统影响较小的低电压等级网络进行简化处理[16]。主干网母线等值模型如图6 所示。

以电网B 区域（图7 中的B 区域）低电压等级网络为例，具体步骤如下：

1）图6 中，将低电压等级网络中的各个发电机j(j=1,2,…,M) 进行等值得到等值发电机，可得等值发电机额定容量SGN与有功出力PGN为：

式中，SGj和PGj分别为第j台发电机的额定容量和有功功率。

图6 主干网母线等值结构

进一步利用加权平均法可得等值机各参数。等值发电机各等值参数为：

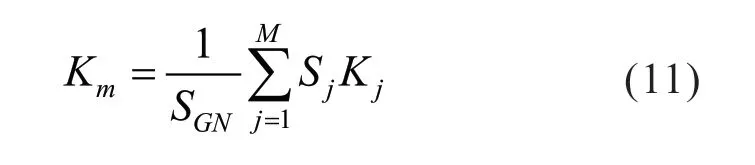
式中，Km、Kj分别为等值发电机和各待化简发电机的模型参数，包括电抗、阻尼系数、惯性常数等。

2）根据图6，等值负荷PLoad的计算公式为：

式中，Pg为等值发电机注入等值母线的有功功率，P为主干网经等值变压器注入低电压等级网络的总有功功率。

1.5 系统状态矩阵建立

建立带水轮机组调速器和PSS2B 的多机系统模型，考虑了调速器的影响和PSS2B 在机组之间的相互影响，可以使优化得到的PSS2B 更好的平息系统振荡。

联立系统网络方程与发电机的线性化方程，并整理式(2)、(4)、(9)，令X为系统状态向量，U为节点电压向量。整理系统状态方程为

系统的状态矩阵为：

可得系统状态矩阵空间方程为

本文通过矩阵求解系统的阻尼比，为设计算法的目标函数提供理论基础。

2 BBO-DE优化算法

2.1 BBO算法

在自然界中，物种生活在不同的栖息地，各个区中在栖息地的生存与每个栖息地的适应度指数(Habitat Suitability Index, HIS) 有直接的关系[17]。BBO 算法采用余弦迁移模型描述自然界中发生的迁移，通过直接迁入迁出操作实现了候选解之间的信息交流[18]。BBO 算法通过随机产生一个数值代替候选解某一维来模拟自然界的种群突变事件[19]。但是BBO 算法通过迁移操作来实现优质解的信息替换不良解的信息，具有很强的开发能力，但是容易造成种群出现趋同现象。随着进化次数的增加，种群中的个体差异和多样性将出现不断减少的趋势，因此极其容易出现“早熟”现象。

2.2 BBO-DE优化算法

针对BBO 算法存在的不足，在改进的BBO算法(BBO-DE) 中，本文提出了一种自适应迁移操作和采用DE 算法变异操作，可以加强算法的寻优能力和开发能力。本文优化算法的改进思路如下：

1)自适应迁移操作

BBO 算法通过直接的迁移操作来进行候选解之间的交流，但是这种操作对于栖息地HIS并不一定能够起到改善作用。本文设计了一种自适应迁移操作，根据问题解中待优化参数的多少，自适应的确定需要进行信息交流的特征信息个数，并在需要迁移参数的某个半径内进行搜索。自适应迁移操作表达式为

式中，k,i1, …,ih=1,2,…,n且不相等；j1, ...,jh= 1, 2 , …,D且不相等。X(i1,j1), ...,X(ih,jh)表示选择的待迁移特征，D为优化参数的个数，ceil表示正向取整。

自适应迁移操作可以使得种群内个体的迁移更加合理，让优秀的个体信息更好的进入较低迁出率的栖息地，扩大栖息地间的信息交流范围，有效地改善了种群内的个体特征和迁入栖息地的HIS。

2）DE 变异操作

BBO 算法通过在解空间中随机产生一个解向量替换原有的解向量来实现变异操作。这种操作在后期的进化中会对解的精度造成影响和减缓算法收敛速度。因此，本文在BBO 算法中，引进改进的DE 变异操作，步骤如下：

在进行变异操作前，在种群中随机选出若干个个体，并在其中随机选出的最优个体分量作为差分变异基，最后，在剩余的个体中随机选择2 个个体作为差分向量。改进后的DE 变异操作保证了差分变异基的质量和个体多样性，其表达式为：

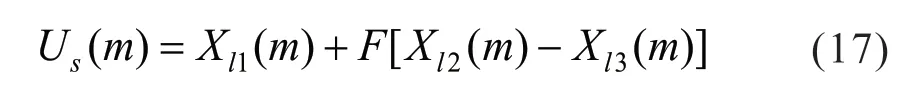
式中，U为变异操作后的值；s为第s个种群的栖息地；X为差分变异基；m为适应度向量的第m个分量。从1 到n中随机选取l1、l2、l3，并使l1、l2、l3和s为4 个互不相等的整数，F为差分因子。

本节改进的DE 变异操作有效保留了速度很快的迁移操作，并且增加了算法的变异能力，使得该算法可以更快更准确的寻找到最优解，有助于得到最佳优化参数。

2.3 PSS目标函数选取

系统的低频振荡与系统特征值有着密切关系。系统中加入PSS 的作用主要是为了系统低频振荡模态的特征值移向整个复平面的左边，从而使得系统的阻尼得到增强。系统阻尼比可以用于评价系统低频振荡抑制效果的性能指标，过小的阻尼比，不利于系统稳定。系统阻尼比公式为：

为了使优化得到的PSS2B 能适应于运行工况多变的电力系统，本文考虑了多种运行工况和多个机电振荡模态的相互作用，选择系统阻尼比作为优化目标函数的评价指标，其数学表述为：

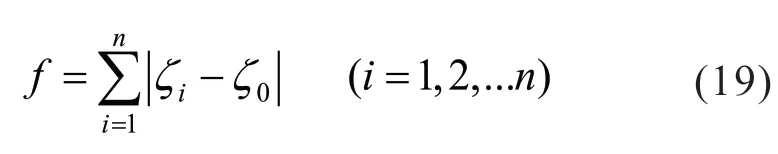
式中，zi是第i 个运行方式下阻尼比的最小值，这里z0为门槛值。

PSS2B 参数优化问题是一个带约束非线性的特征值优化问题，具体约束条件为：

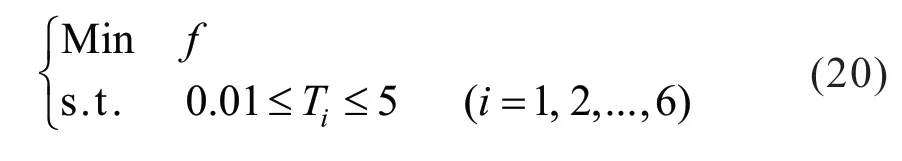
式中，Ti为PSS2B 的补偿环节时间常数T1、T2、T3、T4、T13、T14，具体见图4。

3 算例分析

3.1 电网部分区域特征值分析

为了研究考虑调速器后实际电网中A 区域机组的低频振荡抑制情况，在PSASP 仿真平台中搭建了电网部分区域模型[20]，如图7 所示。图中，A 和B 处于电网末端且互联，与C 等值区域形成一个类似于3 机9 节点的系统。该系统发电机采用3 阶模型，调速器采用PSASP 中的1 型通用调速器模型，励磁系统采用自并励励磁系统，稳定器采用PSS2B 模型。

系统基准容量Sn=100 MVA，Un=230 kV。B 区域机组容量为1200 MW，A 区域2 台机组容量都为360 MW，C 等值部分机组容量为1300 MW。

图7 电网部分区域模型

在PSS2B 优化参数流程中，考虑了系统3种不同的运行工况，分别表示电网中的常规运行工况、重负载运行工况和轻负载运行工况。因此，基于这几种比较有代表性的工况优化得到的PSS2B 参数可以保证系统拥有较好的稳定裕度。表1 为4 台发电机在3 种运行工况下的出力情况，表2 为3 种运行下的系统负荷情况。

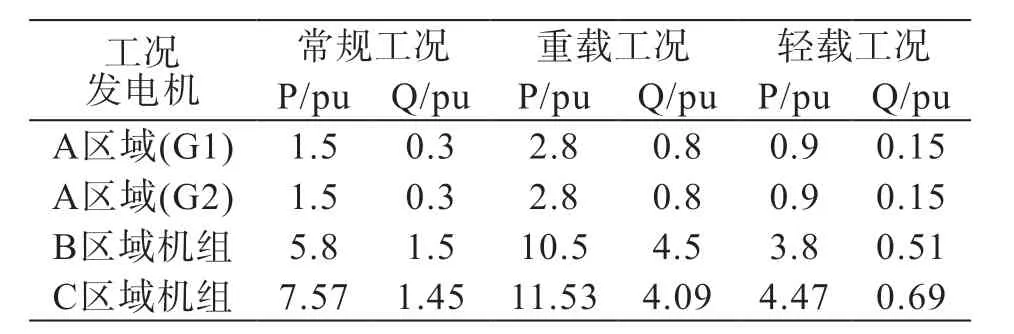
表1 各种工况下发电机出力

表2 各种工况下系统负荷情况

为了分析PSS2B 优化参数抑制低频振荡的效果和不同运行工况下的鲁棒性。本文利用小干扰稳定分析方法计算不同运行工况下系统的阻尼情况。

该系统模型有3 个机电振荡模式，频率都在1Hz 左右。系统加装原PSS2B 后，在常规工况下，系统的3 个机电振荡模式阻尼比分别为11.3%、12.2%和13.9%。在轻工况和重工况运行下，其3 个模式阻尼比中出现了阻尼比小于10% 的情况。系统加装BBODE-SPSS 后，在常规工况和重工况下，系统的机电振荡模式阻尼比都明显大于原PSS2B。在轻工况下，加装BBODE-SPSS 后系统阻尼比只是略大于原PSS2B，效果并不明显。在3 种不同运行工况下，加装BBODE-MPSS 的系统，3 个机电振荡阻尼比都是最优的且都大于20%，说明BBODEMPSS 受系统运行方式的影响较小。通过上述分析可知，BBO-DE 算法中考虑多工况时优化得到的BBODE-MPSS 具有良好的鲁棒性，在提高系统阻尼方面效果明显。

3.2 电网部分区域的时域仿真

本节分别设置三相短路故障和发电机励磁电压加2%的阶跃扰动等2 种典型故障，进行仿真验证系统分别加装原PSS、BBODE-SPSS 和BBODE- MPSS 后对低频振荡的抑制效果。

3.2.1 三相短路

本文在线路2-3 处设置三相短路故障，故障起始时间为1s，持续时间为0.1s。分别在系统 中 加 装 原PSS、BBODE-SPSS 和BBODEMPSS 进行仿真，取不同工况下A 区域(G1 机组)的电磁功率振荡曲线进行比较，如图8(a)～(c)所示。

图8 短路故障下G1机组功率曲线

图8 中，系统安装原PSS2B 时，在常规工况下，系统发生低频振荡，机组电磁功率振荡持续时间长且振荡明显，6.5s 左右振荡得到平息；在轻工况和重工况运行下，机组电磁功率振荡时间变长且振幅有所增加，振荡平息时间约8s。系统安装BBODE-SPSS 时，机组电磁功率的振荡衰减速度比安装原PSS 时快，常规工况下振荡平息时间为3.3s 左右，轻负载工况和重负载工况下振荡平息时间分别为5.5s 和4.5s 左右。系统安装BBODE- MPSS 时，机组电磁功率的振荡衰减速度最快，在3 种不同运行工况下，机组电磁功率振荡平息时间均小于3.5s，说明基于多工况下BBODE 算法优化的BBODE-MPSS 受运行工况变化的影响较小。上述仿真证明了本文优化的BBODE- MPSS 具有较好的鲁棒性。

3.2.2 励磁电压阶跃

励磁电压参考值处设置励磁电压参考值2% 的方波阶跃，故障起始时间为1s，持续时间 为0.1s。 对 安 装 原PSS、BBODE-SPSS 和BBODE-MPSS 的系统进行仿真，取不同工况下A 区域(G1 机组) 的电磁功率振荡曲线进行比较，如图9(a)～(c)所示。

图9 励磁阶跃故障下G1机组功率曲线

图10 典型故障下G1机组功率曲线

由图9(a)～(c)可知，常规运行工况下，系统加装原PSS2B 后，仍然存在低频振荡。系统分别安装BBODE-SPSS 和BBODE-MPSS 后，低频振荡得到较好的抑制。在常规工况下，低频振荡抑制效果最好的是BBODE-MPSS，其次是BBODE-SPSS，但是BBODE-SPSS 的抑制效果只是略好于原PSS 的抑制效果。在重工况和轻工况下，BBODE-SPSS 和原PSS 的抑制效果开始变差，振荡平息时间大于6s。但是BBODEMPSS 基本不受运行工况的影响，依旧能很快平息系统的振荡，振荡平息时间约为3.5s。

上述仿真证明了本文优化的BBODE-MPSS在不同的运行工况下都能较快的平息振荡，说明BBODE-MPSS 具有较好的鲁棒性。本文优化的PSS2B 参数对抑制A 地区水轮机组的低频振荡具备较好的鲁棒性，各种工况下抑制效果都比较明显，基本能在3.5 s 左右平息振荡。

3.3 电网部分区域的时域仿真分析

为了进一步验证本文优化的PSS2B 在实际电网的抑制效果，本文在电网大系统中加装BBODE-SPSS 和BBODE-MPSS 进行仿真验证。分别设置3 相短路故障和励磁参考电压阶跃故障，取A 区域(G1 机组) 的电磁功率振荡曲线行比较，如图10(a)～(b)所示。

由图10(a)～(b)可知，在3 相短路故障和励磁电压阶跃故障时，安装本文优化的BBODESPSS 和BBODE-MPSS 后，系统在抑制低频振荡方面的能力明显优于原PSS2B。通过对比可知，抑制低频振荡效果最优的是BBODEMPSS，其次是BBODE-SPSS。上述仿真证明了本文优化的PSS2B 对电网的低频振荡有较好的抑制效果。

4 结束语

本文通过建立电网部分电网状态矩阵，改进BBO 算法，并对PSS2B 参数进行了优化，得出主要结论如下：

1）考虑了水轮机组调速器对PSS2B 的影响，并根据电网实际情况对励磁系统、调速器和PSS2B 三者提出了合理的简化模型和进行线性化处理，建立了符合电网实际情况的多机线性化模型和状态矩阵。

2）提出一种自适应迁移操作和采用DE 算法变异操作改进了标准BBO 算法，得到本文改进后的BBO 算法（BBO-DE）。根据电网部分区域模型，构建了多机电振荡模式下的目标函数，进行了PSS2B 参数优化。

3）搭建了实际电网部分区域电网模型，在3 种不同运行工况下，通过仿真验证了本文优化出的PSS2B 均能在3.5s 左右平息振荡，并且能适应于系统不同的运行工况，拥有良好的鲁棒性。

4）将本文优化出来的PSS2B 参数代入整个大电网系统中，通过仿真验证了本文建模和优化方法的正确性和有效性。