基于主元分析的水轮机组导轴承异常诊断方法研究

赵明，梁俊宇，李孟阳，杜景琦

（1.云南电网有限责任公司电力科学研究院，昆明 650217；2. 云南电力试验研究院(集团)有限公司，昆明 650217）

0 前言

云南省水电装机占比大，承担电网基本负荷，电网的安全运行与水轮机组运行状态的好坏直接相关。水轮机组导轴承作为水轮发电机组的承力部件, 是转动体和固定体的接触分界面，当轴系失中、轴系振动、轴承制造缺陷、润滑不畅、异物进入等。会由于摩擦等原因产生大量热量，引起轴温快速升高，严重时可能会造成热损坏，导致安全事故以及重大的经济损失[1]。因此监测导轴承的运行状态，并对其进行状态预警，对机组的安全可靠性至关重要。

目前已有的异常诊断方法是将其看作分类问题，采用分类算法进行样本训练并进行异常类的识别，做出设备状态异常状态的判断[2][3]。然而由于大型轴承轴瓦数量多，轴承温度测点数量多，如此众多的测点进入异常诊断算法会造成“维度灾难[4]”问题，严重影响轴承温度异常诊断的效果。

本文基于主元分析方法（PCA），提出了一种水电机组轴承温度异常诊断方法。该方法是一种特征信号提取方法，具有消除数据相关性、降低数据维数等优良性能[5-9]。该方法利用轴承不同位置轴承温度相关性较高的特性，有效克服轴温多测点带来的“维度灾难”问题，当轴承工作异常时，测点温度会偏离正常的温度范围，进而导致模型残差分布发生变化，当残差超出通过历史数据训练的阈值时，提供运行人员异常信息，并检查水轮机组导轴承的工作状态。

1 主元分析方法（PCA）

主元分析（Prinipal Component Analysis,PCA），是一种得到广泛使用的多元统计分析法，可用于对多维数据的降维操作，有效提取多维数据中主要的信息，应用于图像处理、故障诊断和模式识别领域。

PCA 方法首先采集处于正常操作条件下的过程数据，对其进行标准化处理，得到均值为0，方差为1 的数据矩阵X∈RN×m（N为样本采样点数，m为测量变量数），其主元模型为

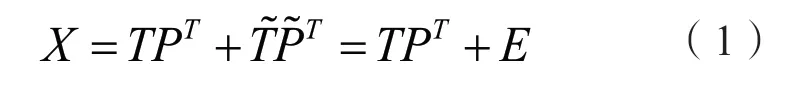
式中，P∈Rm×k，T∈RN×k分别为载荷（投影）矩阵和主元得分矩阵，k表示选取主元的个数，k≤m。P～∈Rm×(m-k)，T～∈RN×(m-k)分 别 为 残差的载荷矩阵和得分矩阵，E∈RN×m为预测残差矩阵。

其中，pi为单位特征向量，λi是特征值，i=1,2,...,m，λ1≥λ2≥...≥λm。 选 取 前k个 特 征向量作为PCA 中的负荷向量，构成负荷矩阵，P=[p1,p2,...,pk]。

通常，主元个数k通过累积百分比方法确定，即前k个主元的累积方差贡献率，通过前k个特征值的和除以所有特征值的和得到，表示这k个主元所能够代表数据方差的比例，即：

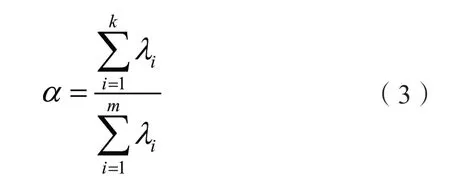
通常，α可以选取为85%、90%、95%，表示主元代表了数据矩阵85%、90%、95% 的信息，即选取的前k个主元代表了数据矩阵X的大部分信息，能够代表元数据矩阵，构成了主元子空间。未被选取的m-k个主元够成了残差子空间，包含了数据矩阵X的剩余信息。当使用PCA 进行异常检测时，常采用T2和SPE 统计量进行过程检测。SPE 统计量和T2统计量分别定义在残差子空间和主元子空间，SPE 指标衡量样本向量在残差空间的投影的变化：

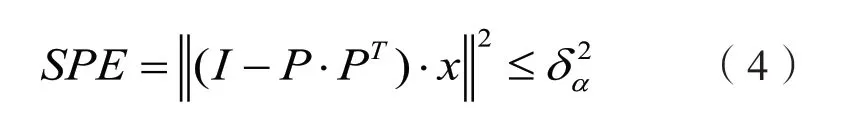
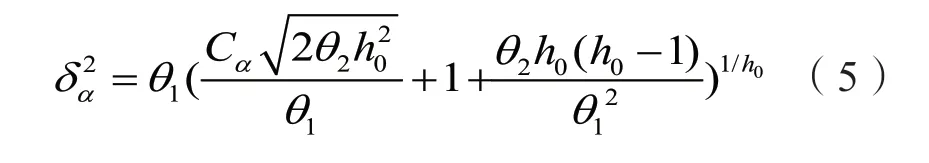
式中，

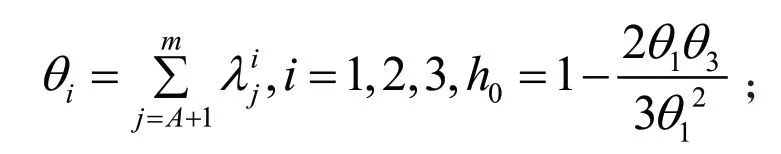
是协方差矩阵的特征值；

Cα为在置信度为α下标准正态分布的阈值。

T2统计量是用来衡量样本向量在主元空间上的变化：

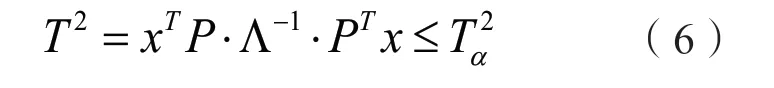
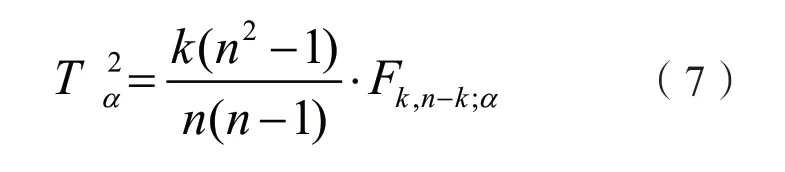
式中，Fk,n-k;α是带有k和n-k个自由度、置信度为α的F 分布值。

对任一组新的测量数据，通过归一化和PCA 计算后，得到的上述两个统计值超过了相应的阈值，则认为过程中出现了异常，即可实现异常的检测。

当过程发生异常时，SPE 可以检测出异常是否发生但是不能指出是哪个变量发生了异常。贡献图是一种非常有用的异常辨识方法[10]，它是基于如下理论假设：对异常检测指标贡献最大的变量是最有可能发生异常的变量。贡献图通过贡献值表征每个变量对SPE 的影响。贡献值实际上是异常在观测变量上的影响，不需要任何有关异常的先验知识就可以产生。

SPE 的贡献图定义如下：

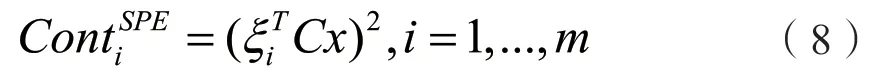
2 水电机组轴承温度预警建模

随着水轮发电机组单机容量的不断增大，大型混流式水轮机组的导轴承体积也不断增大、轴瓦数量不断增多，导轴承一般布置多个传感器，用于监测轴承不同轴瓦的温度，当某块轴瓦发生损坏后，该轴瓦的温度会出现升高，因此需要对每个温度测点进行监视，但传统的异常诊断方法难以监测如此多个参数，因此考虑通过PCA 统计建模方法对其进行异常诊断，首先对正常历史数据通过PCA 方法消除数据相关性、降低数据维数，并得到其得到模型残差分布特性，作为阈值；其次对实时运行数据进行PCA 操作，得到模型残差分布并与阈值比较，如果超出则进行异常报警，并基于SPE 贡献图对异常测点进行诊断。

其异常诊断的具体步骤如下：

步骤一：选择监控变量，提取正常工况下的轴温典型样本。从海量的历史运行数据中筛选出典型数据样本集。典型数据样本集要求：

1）训练数据中所覆盖的状态必须包含系统正常运行状态下所有监测参数动态变化过程，即机组各个典型负荷状态下的监测参数变化过程；

2）训练数据中的状态不能包含异常状态，必须全部为能够表征系统正常运行状态的参数。

步骤二：数据归一化。对于经过上述步骤处理的数据集X*∈RN×m，用下式将各变量值域标准化至[0,1]：

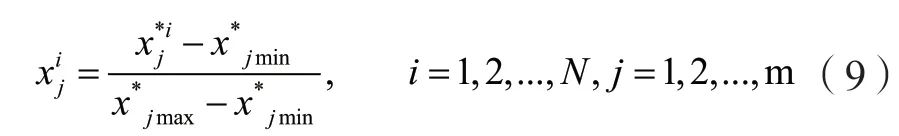
步骤三：对于步骤二中的正常典型样本数据集，建立PCA 主元模型。包括以下步骤：

3）计算前k个主要元素的累积方差贡献率

4）对典型样本数据集做PCA 分解，获得主元子空间和残差子空间。

步骤四：计算典型样本数据集PCA 模型的统计量及相应的阈值。包括SPE 统计量与T2统计量；

步骤五：基于标准典型样本数据集的PCA模型的在线异常检测与诊断。包括以下步骤：

1）在线采集电厂实际运行数据，获得新的数据集，并进行与步骤二同样的标准化。

2）对标准化后的数据，通过PCA 分解计算T2和SPE 统计量，监控其数据是否超过正常状态的阈值。若没有超限，则轴温正常；若超限，则计算每个过程变量对残差T2和SPE 统计量的贡献率，贡献率最大的变量就是可能引起异常的变量。

该方法的具体步骤如下图：

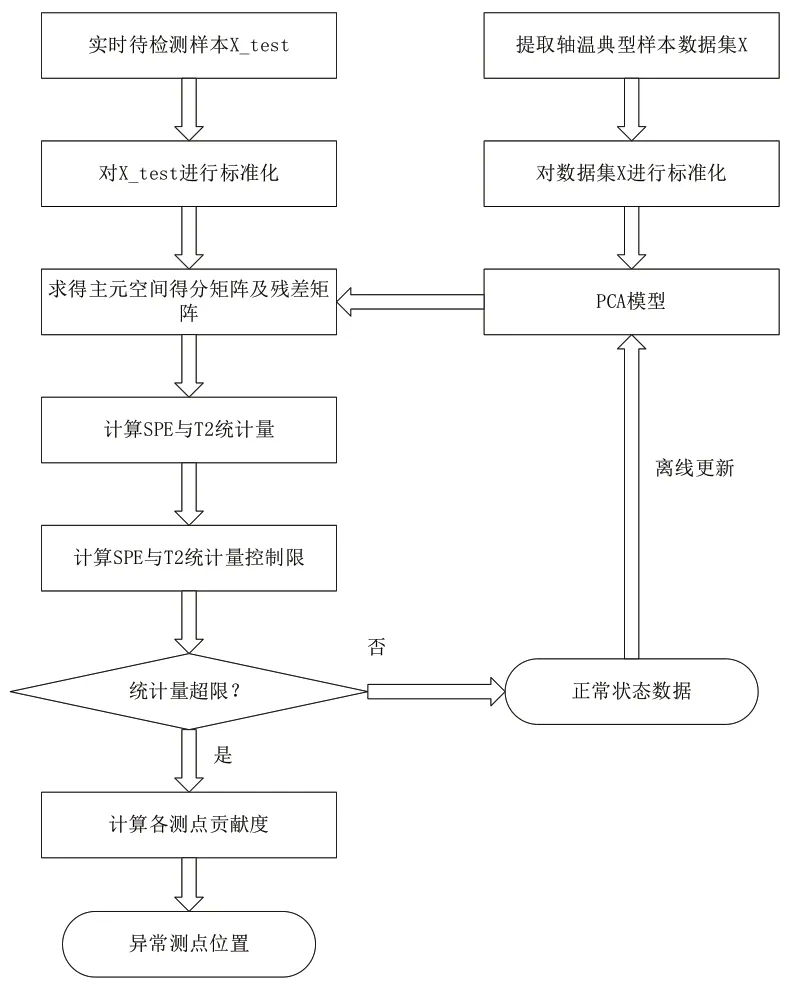
图1 基于PCA方法的主轴温度异常诊断

3 异常诊断模型构建示例

以云南省某水轮机组的上导轴承温度为例，该设备具有30 个温度测点，将该机组四个月的历史运行数据作为训练样本集，经过数据预处理以及样本选择过程，提取1500 条样本数据，构成矩阵规模为1500*30 的训练矩阵。并为此该典型样本数据集建立PCA 主元模型。

首先，对标准典型样本数据集执行协方差分解以计算特征值矩阵，并选择主元的数量。本例中要求累积方差贡献率达到99%，最终求得主元个数为8。计算标准典型样本数据集的PCA 模型的统计量及相应的阈值。包括SPE 统计量与T2统计量，本例中计算的SPE 阈值以及阈值分别为0.012 与23.5。

采用测试数据进行模型的测试，由于采集的测试数据集都是正常数据，SPE 统计量几乎始终未超限（仅有一处误报），为正常状态。T2统计量有少数超限但持续时间很短，可以认为是误报，设备仍可认为是正常状态。最终计算的贡献图见附图未发现有明显异常的测点，如图2～3。

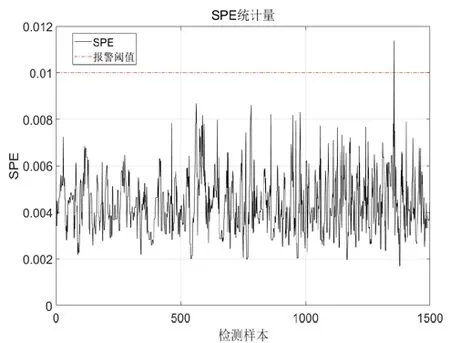
图2 正常数据的 SPE统计量

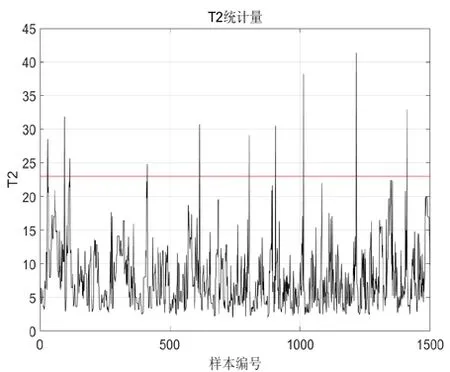
图3 正常数据的T2统计量

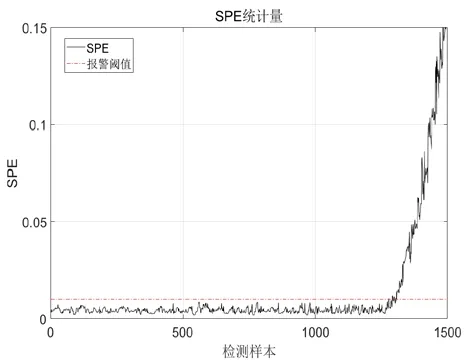
图4 异常数据 SPE统计量图

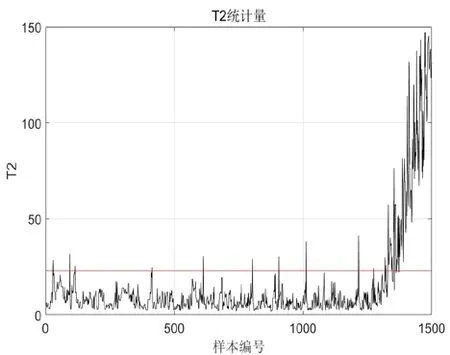
图5 异常数据T2统计量图

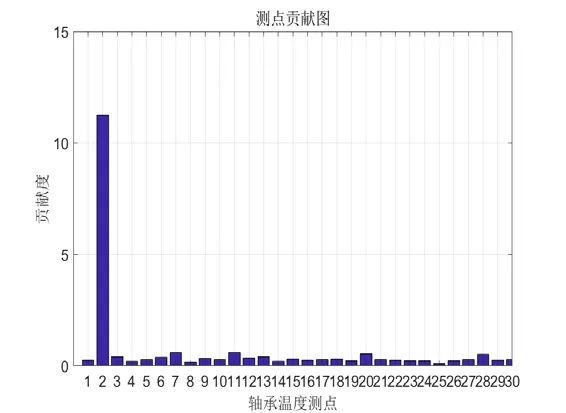
图6 异常数据测点贡献图

为对算法有效性进行验证，假定第二传感器测点位置的轴瓦发生异常，造成温度升高，对在1251～1500 时刻第二传感器测点的温度，在实际值基础上线性提升5℃。

最终结果见下图。从下图可以看出，在1～1250 时刻SPE 统计量始终未超限，为正常状态。在异常段1251～1500 时刻，SPE 统计值与T2统计量显著上升，最终SPE 统计量1294 时刻超限报警，在1321 时刻T2统计值发生超限，此时异常温升大概在1℃左右。最终计算的贡献图见图6，测点2 的贡献量远大于其它，可见PCA 正确的识别了发生异常的测点位置。

4 结束语

与传统的轴承温度异常诊断方法相比，该方法具有如下优点：

1）算法流程简单实用，条件容易满足，效率较高；

2）由于轴温传感器测点之间的强线性关系，不会产生维度灾难，即使测点很多的情况下也可以充分挖掘历史数据当中的信息，错报误报率小，具有更加合理的参考意义；

3）易于软件实现，可以较为方便地融入水电厂设备在线监测系统。