基于一种改进K-means聚类方法的岩体结构面优势分组研究

徐倚晴，郝朝阳，权雪瑞

（吉林省长春市朝阳区吉林大学朝阳校区，吉林 长春 130061）

复杂的地质作用会影响着岩石的发育，会形成各种不同类型和规模的结构面[1]。在岩体变形或破坏时，主要沿着岩体结构面开裂或破坏[2]。研究结构面的裂隙，对裂隙各参数进行实地测量进而应用统计方法进行研究是十分有利于工程应用的。

常见的岩体结构面裂隙的统计分析方法是将具有某些共同特征的裂隙归类，按照结构面裂隙的产出状态进行优势分组。Behzad等采用K-means均值聚类算法进行岩体结构面优势分组，但是传统算法中的K是人为定义的，主观性很强，这就导致了该算法结果的不确定性。

鉴于以上的不足，本文首先采取Canopy算法应用在K-means算法之前的粗聚类。由此，通过Canopy算法将含孤值点的聚类簇直接去除，有利于抗干扰。将Canopy算法筛选的每个Canopy的质心，作为K-means算法的初始分类中心，这样就有效的解决了算法结果不确定性的问题。并且改进后的K-means算法具有速度快、效率高等优点，应用于工程实例进行优势分组研究非常具有优势。

1 数学模型建立

1.1 结构面产状数据预处理

通常以野外调查的方式确定岩体结构面的倾向（0≤α≤360°）、倾角（0≤β≤90°），并以这两个参数为主来描述结构面在岩体中所处的空间延伸方位以及倾斜程度。一般采用上半球投影法对岩体结构面进行描述，忽略结构面的厚度，用一个三维空间内的平面来代替原结构面。在该坐标系中，结构面的单位法向量n=（x，y，z）表达式如下。

1.2 相似性度量

为了避免在上半球投影中采用欧式距离度量发生的陡倾角结构面过分组情况，采用两平面单位法向量之间夹角的正弦值作为相似性度量。距离公式表达式如下：

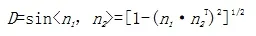
1.3 改进K-means算法原理

该算法针对数据集X={x1，x2，x3，…，xn}，预定义合适的T1、T2（T1＞T2）两个阈值。将数据集向量化后，随机选定一个数据作为第一个Canopy的质心，计算数据点之间的距离，并与设定的阈值进行比较来确定各数据点对于每一个Canopy的归属。多次迭代后，将数据集划分为几个部分。

经过Canopy算法初步聚类，得出的分组结果中心，作为K-means算法聚类分组的初始中心。根据距离公式，按照距离最近原则，将数据集中未分类的各数据划分到最适合的聚类组中，并按均值的方式重新计算分配后的聚类组质心。多次迭代直到聚类组质心几乎不再发生偏移，或偏移量小于某一设定的精确度。K-means算法步骤具体不再赘述。

1.4 算法可行性检验

为了检验改进后的算法的有效性，采用随机生成模拟数据的方法，共生成4组结构面，其中结构面的倾向和倾角服从二维正态分布。具体结构面产状均值等参数如下表所示：

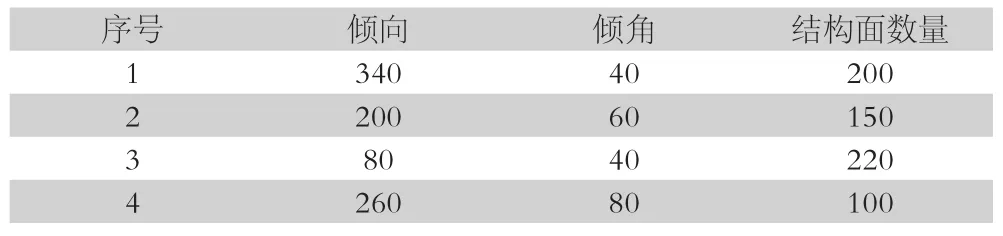
表1 结构面随机模拟参数

经过初始调整，确定阈值参数为T1=0.80，T2=0.77。应用该算法分组，得出结果如图1，验证了算法的可行性。

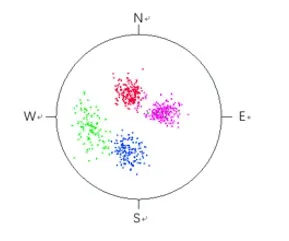
图1 模拟数据分组结果极点图

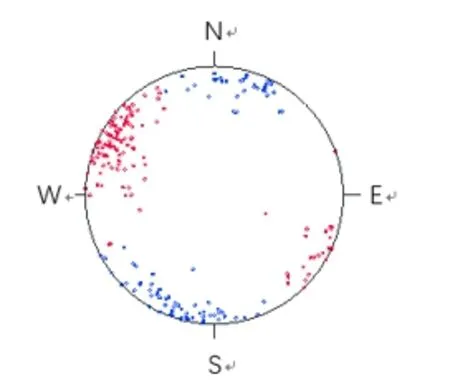
图2 实测数据分组结果极点图

2 工程实例

大藤峡水利枢纽水库区位于桂中、桂东北地区，现场主要调查了出露在28#坝段下游的该地层。此地层属于泥盆系下统郁江阶下段，岩性主要为灰～灰黑色灰岩、白云质灰岩。现场裂隙极其发育，裂隙特征也各有不同[3]。现场测得该坝段岩体裂隙总计277条。根据以上算法，通过交叉验证调整参数，确定Canopy算法分组阈值大小为T1=0.99，T2=0.97，并结合改进后的算法对测得的现场裂隙进行优势分组，结果如图2。

由分组结果可知，原始测量裂隙分两组最为合理。其中第一组裂隙为152.97°∠82.61°，第二组裂隙为266.57°∠79°。分组后的结果可详细反映与岩体结构面性质，且为岩体稳定性的分析评价、工程的设计提供更详细的信息依据。

3 结语

对岩体的结构面裂隙进行数值化统计分析是岩体力学领域的重要课题之一。本文提出了基于应用Canopy优化K-means算法的岩体结构面优势分组分析方法，可以得出：根据人工生成的4组结构面数据以及现场勘测的分离性较好的2组结构面数据，验证了完善后的算法确实可靠，极大地降低了对中心点选取的干扰。并表明该方法在解决大型岩体结构面数据优势分组问题时，能获得不错的分组效果，提供可靠的依据。