安装偏角对城市综合管廊支架受力影响分析★

许广州 董 聪 杨会兵 曹广勇石仁生 陈开军 魏国强 阮 磊 翟朝娇

(1.合肥福临工程监理有限公司，安徽 合肥 230000；2.安徽建筑大学建筑结构与地下工程安徽省重点实验室，安徽 合肥 230601；.合肥高新区综合管廊建设办公室，安徽 合肥 230088； 4.上海新光工程咨询有限公司，上海 200437)

0 引言

我国许多城市市政管线都埋在地下表面，造成地下空间拥挤和混乱，为了使城市地下空间资源充分得到利用，地下综合管廊应运而生。国内外关于综合管廊支架有不少研究，仲良[1]对综合管廊支架选用和受力计算进行了研究，王智文[2]和史伟伟[3]详细介绍了综合管廊中装配式支架安装工艺和要求，薛达[4]通过有限元分析软件研究了冷弯C型钢梁在弯矩和扭矩共同作用下的受力性能。城市综合管廊一般设计使用年限为100年，管廊支架在地下潮湿的环境中受长时间的荷载，经常会发生支架塌落，而装配不规范产生的偏角会加剧这种情况的发生。本文通过实验还原了现实施工中的安装偏角，研究了安装偏角对城市综合管廊支架受力影响，并通过ABAQUS有限元分析软件模拟验证试验的准确性，并提出了几条建议。

1 实验

1.1 工程背景

本项目位于合肥市高新区，建设内容包括综合管廊工程和入廊污水管线，总投资20.90亿元。其中综合管廊工程总长20.29 km，位于明珠大道等共7条道路，主要建设内容为管廊主体以及配套的电气、监控、照明、检测、给排水、消防、通风、控制中心等工程，建成后满足区域电力、通信、给水、再生水、供热、污水及燃气等管线的敷设需求，其建设状况如图1所示。

1.2 实验内容

综合管廊支架体系主要为管廊内的管道及桥架起到支撑及固定作用，传统的地下室及地道内的支架大多采用后锚固法施工，即先在施工现场加工支架，再通过膨胀螺栓与结构进行固定。由于现场安装过程存在偏差，两个固定螺栓所在直线与垂线出现偏角，支架截面在竖直方向出现偏转，示意图如图2所示。我们分别在100 N,150 N和200 N的荷载下选取0°，5°，10°，15°和20°的偏斜角度进行实验。

1.3 实验步骤

1)根据数值计算结果在固定端卷边上部和固定端支架下部开孔处粘贴电阻应变片并连接动态应变仪来计算应力变化，焊脚处无法粘贴应变片仅进行数值模拟，如图3所示；在梁悬臂端的上方将激光位移计固定，位移计与梁悬臂端的距离约为10 cm处，在梁悬臂端上选取一点并将激光对准该点，来测量支架悬臂端挠度变化。

2)将支架用膨胀螺栓固定在垂直混凝土墙上，通过改变膨胀螺丝位置来改变安装偏角，偏角分别取0°，5°，10°，15°和20°。

3)在施加载荷之前，按一次应变仪面板上的“平衡”按钮(调零)并记录激光位移计的读数，然后开始用砝码给支架添加三个荷载并在应变仪上读取并记录相应的各点处应变计的读数和变化后激光位移计的读数，如图4所示。

4)分别在100 N,150 N和200 N的荷载下进行实验。实验至少做两遍，取线性较好的一组作为本次实验的数据。

2 数值模拟方法

2.1 模拟内容

我们分别取0°，5°，10°，15°和20°的偏斜角度，用ABAQUS[5]进行数值模拟，得出在荷载作用下偏角对支架挠度的影响，求出最大应力点得到最危险截面。然后与实验进行对比得到结论。

2.2 模型建立

简支梁长0.7 m，由C字型钢与底座焊接而成，支架下部有椭圆形开孔。横截面尺寸如图5所示，材料选用Q235碳素钢材料，其性质如表1所示。

表1 材料性质

以HYAT型通信电缆中重量最重的电缆为理论计算荷载，理论计算取最大间距1 500 mm，为保证预留荷载余量，荷载按100 N,150 N和200 N计算，分别取0°，5°，10°，15°和20°的偏转角度进行模拟。

2.3 模型假定

1)管廊支架固定端由螺栓固定，没有位移和转角，假定支架固定端为完全固结状态，简化为悬臂梁进行计算。

2)假设在管廊支架上放置三排电缆，其荷载在实际运用中为线荷载，截取一段线荷载将其假定成集中荷载作用在管廊支架上。

2.4 分析结果

在模拟中选取正常安装和10°偏角，支架上施加三个150 N的集中荷载，分析得到Mises应力图。在正常安装时支架向下发生弯曲，如图6所示，Mises应力最大值50.87 MPa，出现在支架下部靠近固定端椭圆开孔处的中间位置；在支架上部的对应位置为上部应力最大点，Mises应力最大值为41.87 MPa，应力沿支架方向向两端逐渐减小，两点连线所在与轴线垂直的截面为应力最大平面，如图7所示；悬臂端挠度为1.02 mm。

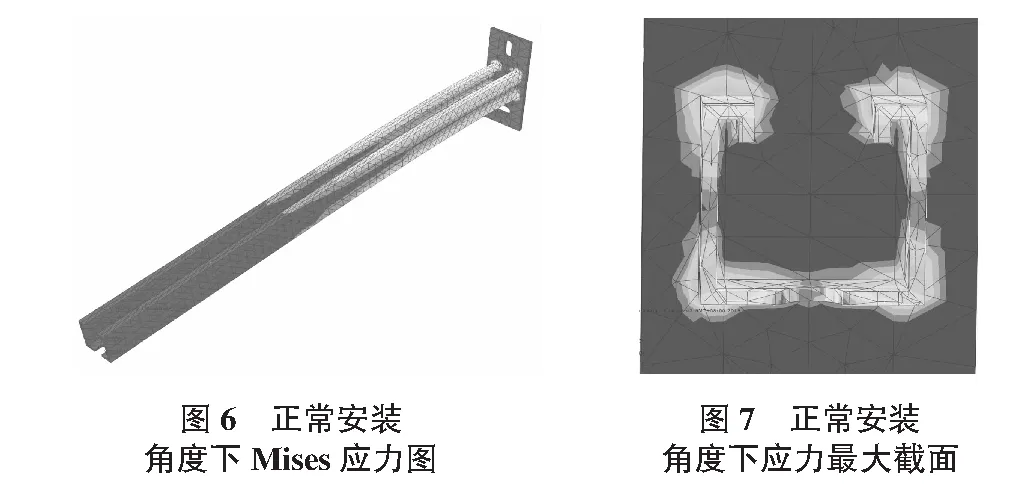
当安装出现沿顺时针方向10°偏角时，支架在出现向下弯曲的同时也出现了扭转变形，如图8所示，Mises应力最大值为68.09 MPa，出现在支架右下角焊接处，应力分布集中；在支架右上角内侧的焊接处为上部应力最大点，Mises应力最大值为62.21 MPa，冷弯C字型钢与底座焊机平面为应力最大截面，如图9所示，应力沿支架方向向悬臂端逐渐减小；悬臂端竖向最小挠度为0.97 mm。

3 试验结果与模拟实验对比分析

结合试验与数值模拟结果，得出以下结论:

1)随着偏转角度的增大，悬臂端挠度先减小后增大。为了说明此现象，我们在CAD中画出横截面以质心为原点建立坐标系，随着偏角的增加截面惯性矩I如表2所示。

表2 截面惯性矩

由抗弯刚度W=EI可知,弹性模量E只与材料组成及其型号有关，故抗弯刚度与惯性矩呈正相关。由表2可得随着偏转角度的增加竖向抗弯刚度增加水平抗弯刚度减小，与实验与数值模拟中0°～10°的悬臂端挠度变化与理论计算符合；10°～20°的悬臂端挠度变化随着角度的增大而略微增大，这是由于支架的扭转变形导致的。仲良[1]提出荷载下支架的形变不能超过L/100，其中L为悬臂梁长度。而实验中最大挠度为4.07 mm小于规定里的7 mm，故在仅有的荷载下支架的形变仍在允许范围内，但偏角不宜超过10°(见图10)。

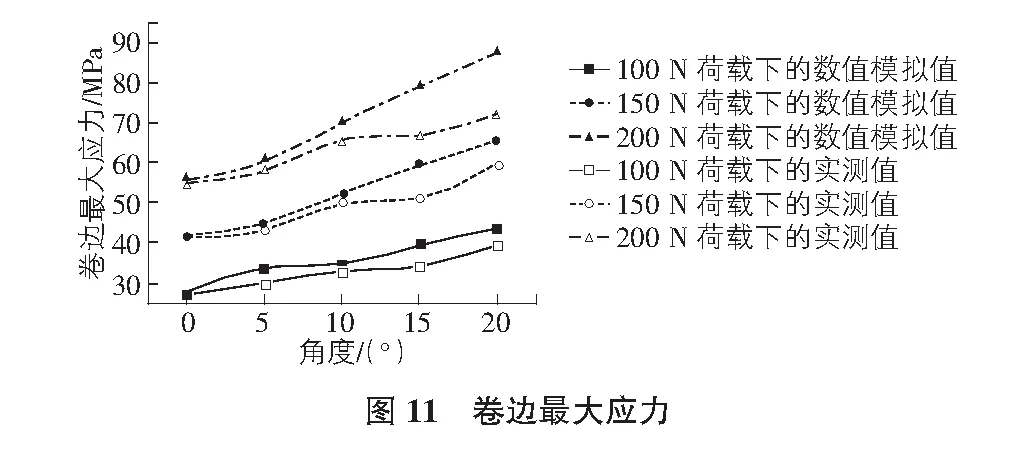
2)在正常安装时支架卷边的最大应力出现在靠近固定端的上部，支架下部最大应力出现在靠近固定端的开孔部分，下部应力大于上部应力。当安装出现偏角后支架卷边的最大应力处出现在偏转方向一侧的卷边上部，支架下部最大应力出现在偏转方向一侧的开孔处，上部应力大于下部应力。由图11，图12可以看出随着偏转的增大在0°～5°时卷边上部的应力增加比较缓慢，5°以后应力快速增加，而支架下部应力增加比较平稳。

3)在正常安装时焊脚处应力较小，随着转角度的出现焊脚处的应力迅速增大，偏转方向一侧的卷边内侧焊脚成为支架上部最大应力处，偏转方向一侧的下部焊脚成为支架下部最大应力处，且下部焊脚应力大于卷边焊脚，随着角度的增加应力增加变缓慢，见图13。

4 误差分析

通过比较，ABAQUS有限元数值分析能够得到与实验基本相符的结果，但是两种方法计算的结果存在部分差异，经过分析可能原因有以下几点：

1)模拟中有限元单元假设具有均匀、各向同性、单元间接触形式统一的特点，而实际工程中支架材料结构较为复杂，C字型钢与底座焊接处存在焊接残余应力，支架可能存在几何缺陷导致应力分布的改变，无法通过有限元建模完整呈现出来。

2)模型建立中假设固定端完全固定，而实验和工程实践中仅靠两根螺栓无法实现完全固定，故导致模拟挠度和实验挠度差别较大。

5 结论

本文通过实验还原了现实施工中的安装偏角，在100 N,150 N和200 N荷载下分别取了0°，5°，10°，15°和20°的偏转角度进行了实验，并用ABAQUS进行数值模拟比较，可得到以下结论：

1)悬臂端竖向挠度随着偏转角度先减小后增加。

2)在正常安装情况下应力最大值出现在支架下部靠近固定端椭圆开孔处的中间位置，随着偏转角度的增加，应力最大处出现在偏转方向一侧的下部焊脚，而且应力大于正常安装时的最大应力，应力分布更为集中。

3)综合实验和ABAQUS数值模拟发现，悬臂端挠度在10°时最小，各点应力在正常安装下最小，在偏角大于5°时应力增长较快，所以安装时应尽量减少偏角的发生，如果有偏角的存在应控制在5°范围内。

解决安装偏角问题的关键在于预防。施工单位在进行施工时应严格按照规范要求进行，当偏角大于5°时应重新安装支架；当偏角小于5°时，支架长时间在潮湿环境中工作，支架焊接处因难以防腐导致非常容易破坏，故应对焊接处做重点防腐处理，如涂覆防腐材料[6]。当焊脚处出现腐蚀时应及时更换新的支架，以防止支架发生塌落。