环氧树脂胶粘接的对接结构多轴疲劳寿命预测

李 慧，张 军，李海宇，申浩中，魏新利

(郑州大学化工与能源学院，郑州 450001)

粘接是借助胶黏剂的粘接力将同种或异种材料连接在一起的技术．近年来，胶黏剂迅猛发展，广泛应用于各个领域，在航空航天、汽车、电子电器、化工医药等领域有着举足轻重的地位[1-2]．但在实际使用中，粘接结构必然要经历多轴载荷循环作用，长期如此将会导致疲劳损伤和粘接结构的破坏．因此，对粘接结构的多轴疲劳性能深入研究具有重要的实际意义，使其在全寿命周期内保持完整性和可靠性．

工程材料的疲劳寿命是其工程应用必要数据，然而，在多轴载荷作用下的循环应力、应变响应非常复杂，材料和结构的疲劳性能很难描述．多轴疲劳寿命预测理论基本可以分为3 种，即等效应力-应变法、能量法和临界面法．其中，临界面法最早由Brown 等[3]提出，因其有明确的物理意义，预测结果与实验结果更为接近，而得到众多研究学者的青睐．该方法选取最大正应变面或最大剪应变面作为临界面，通过计算临界面上的应力、应变历史，并转化为损伤参量进行疲劳寿命预测．基于临界面法的多轴疲劳寿命预测模型有SWT、FS、CHX 等[4-6]，但是，由于其损伤参量选择的局限性，仍没有一个模型能够适用于各种材料和加载情况，都要根据实际材料和结构特点对疲劳寿命预测模型进行修改．

材料的疲劳实验和疲劳寿命预测以前主要针对金属材料[7-9]，而随着非金属材料的广泛应用，近年来，对非金属材料如粘接剂、橡胶、塑料、高分子复合等材料的疲劳性能和寿命预测也越来越受到重视.段小成等[10]研究了变幅载荷下，填充型天然橡胶的单轴疲劳特性及其寿命预测．以应变比为基础建立相关的疲劳寿命预测模型，最终证明了该模型在橡胶隔振器前期寿命预测的可行性．杜美娜等[11]研究了粘接层厚度、载荷加载频率以及加载平均应力对丙烯酸酯搭接结构疲劳性能的影响．王小会等[12]对几种有机硅密封胶的物理特性及疲劳性能进行了实验研究，发现弹性模量变化是疲劳损伤的主要原因．王文涛等[13]对橡胶材料进行了单轴拉伸疲劳实验，建立了相应的疲劳寿命预测模型，该模型能够给出较为准确的预测结果．Wang 等[14]选取PEEK 材质进行了单轴多轴疲劳实验，并应用SWT、FS、CXH 3 种模型对其进行寿命预测，预测结果各有好坏．根据裂纹扩展对疲劳寿命的影响，修正SWT 模型，并给出了较好的预测结果．Tao 等[15-16]研究了平均应力应变和剪切幅值等因素对环氧树脂胶单轴疲劳寿命的影响，以应力法、应变法和能量法分别对其寿命进行了预测，证明实验结果和预测结果有很好的一致性．Lin 等[17]对各向异性导电胶膜的单轴棘轮行为进行了研究，结果表明棘轮应变幅和棘轮应变率与应力幅值及平均应力成正比，应力循环之间会相互影响．Lu 等[18]研究聚碳酸酯(PC)的单轴疲劳及其随时间变化规律．实验结果表明，PC 的疲劳寿命与实验温度有很大的关系，棘轮应变和棘轮应变率随实验温度的升高而增大，疲劳断裂发生在较高温度的载荷情况下．

虽然对非金属材料的多轴疲劳寿命预测方面研究较多，但这些研究主要是对材料本身的研究，而对于粘接结构多轴疲劳实验研究和寿命预测的研究还很少，主要原因是用于多轴疲劳的对接试件制作困难，以及对其寿命预测准确性偏低．

本文采用铝合金为基材、环氧树脂胶为粘接剂的中空对接试件，在不同的加载路径、不同的等效应力幅值下对其进行了多轴疲劳实验；根据实验结果确定了粘接结构单轴和多轴疲劳的基本参数，并应用SWT、FS 和CXH 3 种模型对疲劳寿命进行了预测.根据粘接结构的断裂特点，对CXH 模型进行了修正，增加了临界面影响因子，采用修正的疲劳寿命预测模型对实验结果进行了分析．

1 试件制作和实验

1.1 试件材料及制备

试件粘接基材选用6061-T6 铝合金，粘接剂为E-44 环氧树脂胶和EP-1 固化剂．用360 目砂纸对基材粘接面进行打磨，保证其表面平整及粗糙度合适．用75%医用酒精对粘接面进行冲洗，去除残留的杂质．再将粘接基材放入电热鼓风干燥箱中进行加热干燥，温度控制在60 ℃左右．为保证对接试件的同轴度和相同的粘接厚度，按照美国ASTM D2095—96 标准，实验设计了一套对接试件的制作模具，如图1 所示．

试件制作时，首先把下面的铝合金管用压板固定在V 形槽中，上下V 形槽在一条直线上，从而保证对接的同轴度．为了粘接时胶黏剂不流入铝合金管内，在管内塞入聚丙烯棒，这种材料与环氧树脂胶不粘接；同时，在管外套上聚丙烯的锥形漏斗，防止胶黏剂流淌．之后，上面的铝合金管用压板也固定在V形槽中，对接表面均匀注入胶黏剂，旋转推进螺栓，使上下铝合金管对接，用定位环确定粘接厚度，一组试件为6 个．粘接后，试件连同模具一起，放置在型号为DHG-9030 干燥箱里，温度设定60 ℃，干燥时间6 h．最后，拆除模具取出固化的试件，去除锥形漏斗和聚丙烯塞棒，打磨粘接层溢出的胶体．对接试件的结构尺寸和实验中的试件如图2 所示．

图1 圆柱对接试件制作模具Fig.1 Mold for manufacturing cylindrical butt-joints

1.2 实验过程及结果

本实验在EUM-25k20 电子万能拉扭试验机上完成，通过载荷控制循环加载，采用正弦波加载，循环周期为4 s，实验在室温条件下进行，由自动采集系统获得实验数据．

本文应用4 种加载路径进行疲劳实验，如图3 所示．由轴向应力与剪切应力关系，即定义以下4 种加载路径：单轴拉压路径，单轴扭转路径，比例路径，非比例的圆路径．每种加载路径进行了5 种等效应力幅值实验，平均应力都设置为0．具体疲劳实验数据和结果见表1．

通过稳油降水措施在该区块的应用，对区块、单井进行分析，在积极治理低效无效井的同时，加大油水井措施力度，加强节能新工艺的推广应用，防止有效益井效益类别下滑及新低效井的产生，巩固了区块开发效益。共实施压裂、补孔、堵水、调参、调冲、间抽等各类调整共1109井次，与运行计划对比，实现水驱年控水16.1×104m3、年控液11.9×104m3、聚驱年控液 7.3×104t，节电 505.34×104kWh，节气19.2×104m3，年收益1.33亿元。

图2 试件与结构尺寸Fig.2 Specimen and structure dimension

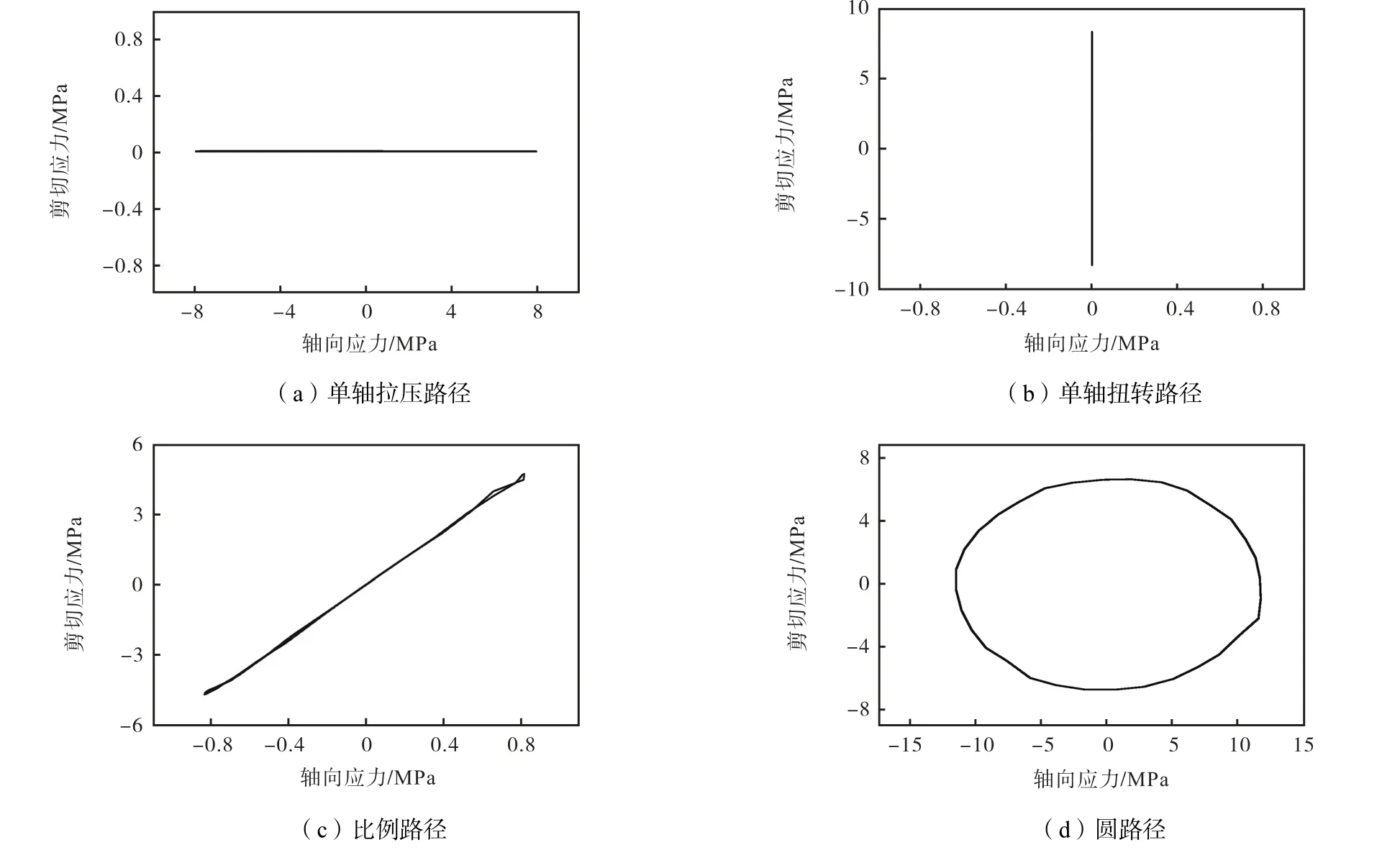
图3 加载路径示意Fig.3 Schematic of loading paths

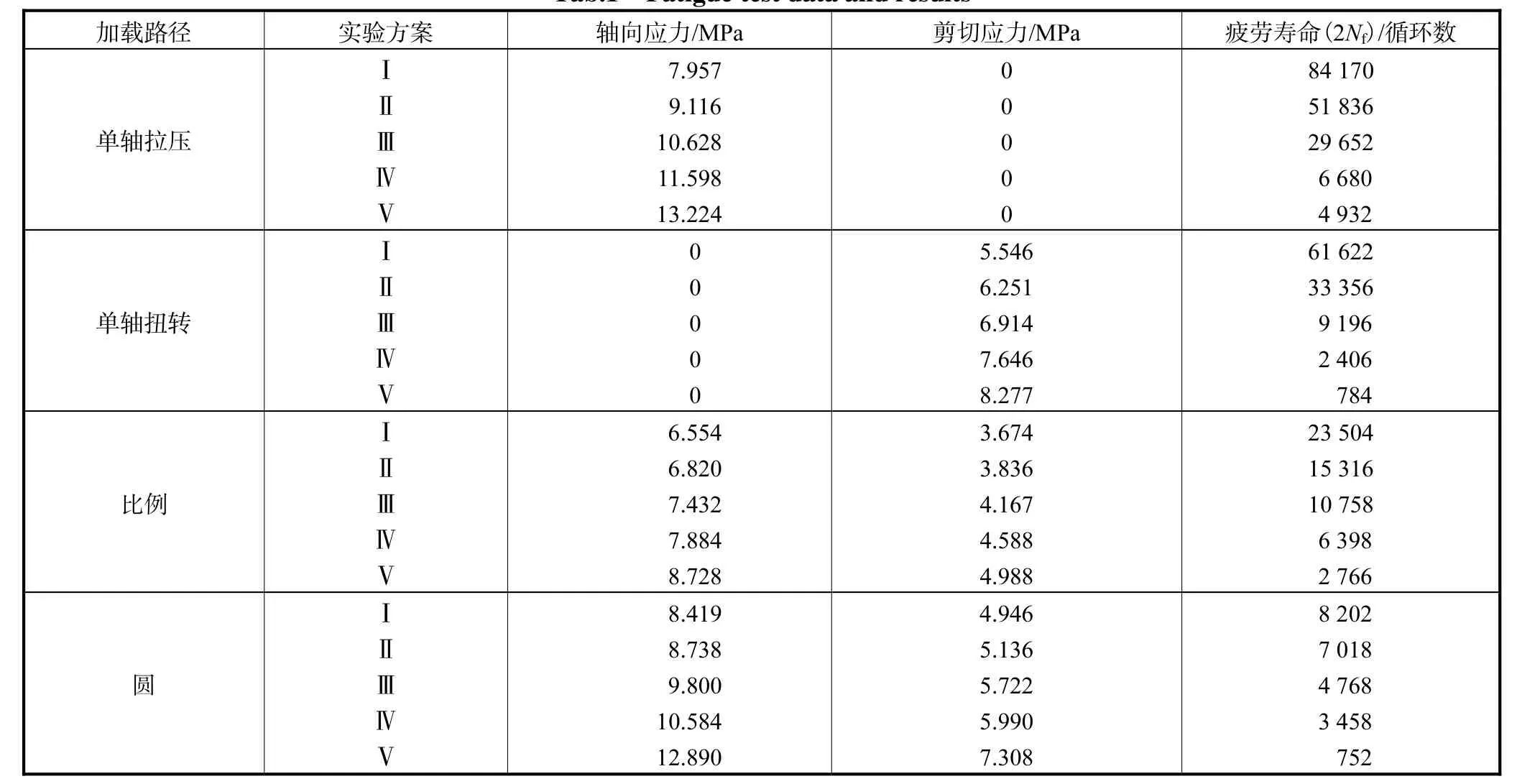
表1 疲劳实验数据和结果Tab.1 Fatigue test data and results

2 理论分析及参数计算

通过实验机上的传感器得到试件拉压及扭转的载荷、扭矩、位移和转角．应用以下公式进行计算得到轴向应力与剪切应力，以及轴向应变与剪应变．计算公式和各变量定义如下.

轴应力和剪应力的公式分别为

式中：F和M分别为实验中加载的载荷和扭矩；D和d分别为试件的外径和内径．本文所采用的试件非严格意义薄壁试件，故将相对厚度纳入公式中.

轴应变和剪应变的公式分别为

式中：l0为粘接层的原始长度；l 为粘接层拉伸(或者压缩)后的长度；α为扭转角．为了考虑粘接结构对剪应变的影响，此处引入长度系数为粘接层厚度，lt为试件总长度．

通过对接结构的单轴拉伸和扭转实验，得到材料的基本参数弹性模量、剪切模量和泊松比等参数[19]；比例和非比例路径下寿命预测所需要的参数，如拉伸和扭转的总应变幅、弹性应变幅和塑性应变幅，通过单轴拉压和单轴扭转实验结果获得，如表2 和表3

所示．

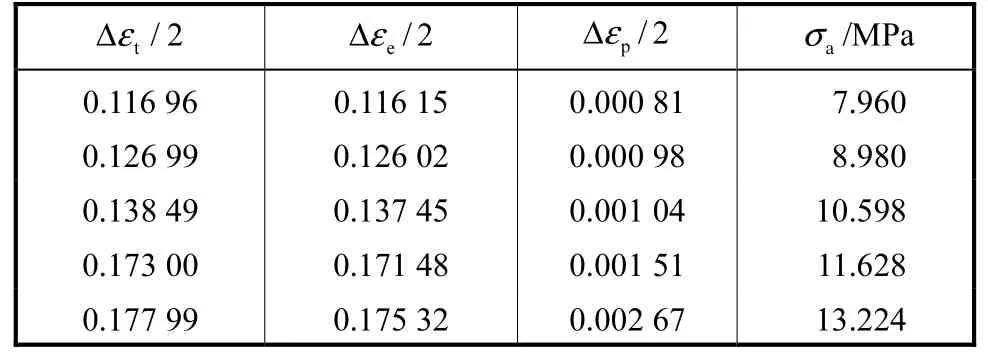
表2 单轴拉压疲劳实验参数Tab.2 Uniaxial tension-compression fatigue parameters

表3 单轴扭转疲劳实验参数Tab.3 Uniaxial torsion fatigue parameters

其他材料常数通过Coffin-Manson 关系拟合获得，如表4 所示．单轴拉压Coffin-Manson 公式的形式为

表4 对接粘接结构的材料常数Tab.4 Material constants of epoxy resin bonding butt-joints

3 疲劳寿命预测

3.1 Smith-Watson-Topper模型

SWT(Smith-Watson-Topper)疲劳寿命预测模型，主要是考虑在最大正应变或正应力平面上的裂纹扩展而导致材料失效，它同时考虑了循环应变幅值和材料的最大应力产生的损伤．尽管裂纹萌生于剪平面，但是垂直于最大正应变和正应力方向的裂纹扩展是影响疲劳寿命的主要因素，因此将最大主应变幅和最大主应变平面上的最大拉应力作为损伤参量，给出模型

图4 SWT模型疲劳寿命预测结果与实验对比Fig.4 Comparison of experimental fatigue lives with predictions using SWT model

3.2 Fatemi-Socie模型

FS(Fatemi-Socie)疲劳寿命预测模型是一种基于剪应变作为主要损伤量的模型，该模型引入非比例加载引起的剪应变平面的法向应力作为另一个损伤量，其模型方程式为

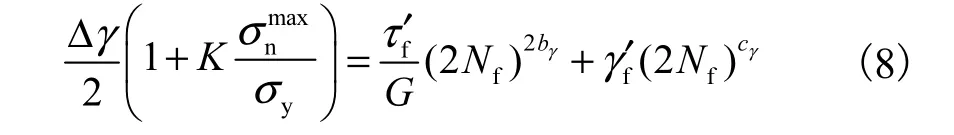
图5 FS模型疲劳寿命预测结果与实验对比Fig.5 Comparison of experimental fatigue lives with predictions using FS model

图5 为用FS 模型预测的寿命与实测寿命的对比，从图中可以看到，所有数据点都落在2 倍误差范围下边，表明基于最大剪应变平面的FS 模型预测对接结构的多轴疲劳寿命过于保守．与SWT 模型相比，FS 模型只考虑剪应变与其面上的法向正应力，忽略了正应变及正应力对粘接结构破坏的影响，远远低估了两种路径疲劳寿命．

3.3 Chen-Xu-Huang模型

CXH(Chen-Xu-Huan)多轴疲劳寿命预测模型是一种结合能量密度和临界面法的混合模型，分别选择最大正应变面和最大剪应变面作为临界面，同时，也考虑了两个临界面上两个方向的能量密度对其损伤的影响．拉伸开裂行为的预测模型表达式为

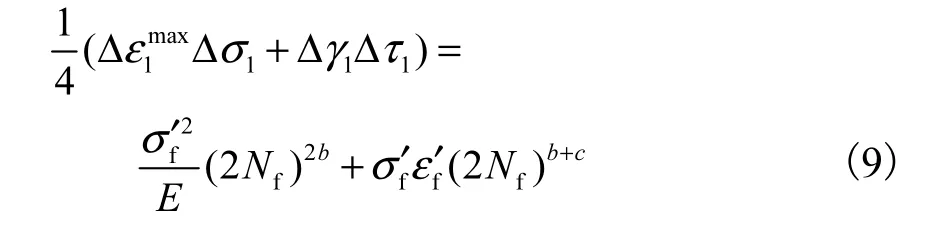
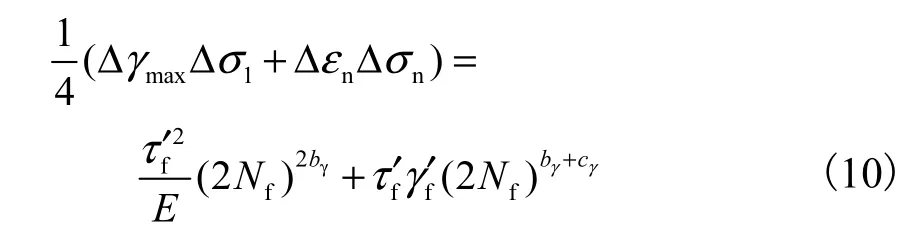
图6 为CXH 模型预测结果与实验结果的对比.预测结果显示，比例路径和圆路径的寿命数据点都有落在2 倍误差范围内的，即使没有落在2 倍误差范围内，两个路径的寿命数据点都在2 倍误差线上边界附近，且预测结果较为集中，但CXH 模型整体预测结果是危险的．由于该模型以最大正应变面为临界面，同时考虑临界面上的剪应变和剪应力的影响，预测结果比前两种模型预测得都好．说明对于粘接结构，单独考虑剪应变或者正应变的某一项，不能较好地预测多轴疲劳寿命，要同时考虑两个方向的应变且比例要有限定．

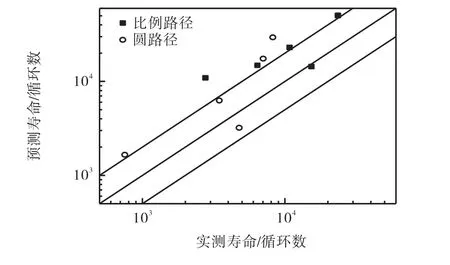
图6 CXH模型疲劳寿命预测结果与实验对比Fig.6 Comparison of experimental fatigue lives with predictions using Chen-Xu-Huang model

3.4 修正CXH模型

从前面3 个模型的预测结果可以发现：SWT 模型把最大正应变面作为临界面，仅考虑拉伸项损伤的影响，寿命预测值偏低．而FS 模型只考虑剪应变与其面上的法向正应力对疲劳损伤影响，忽略了正应变及正应力对粘接结构疲劳破坏的影响，两种路径疲劳寿命预测远低于实验结果．然而，CXH 模型以最大正应变面为临界面，同时考虑临界面上的剪应变和剪应力的影响，预测结果优于其他两个模型，但由于没有考虑到损伤面上两个方向损伤的比重，所以，预测结果与实际结果也存在偏差．实验中发现，粘接结构的断裂强度是由粘接材料强度和粘接界面强度共同

决定，其断裂方式可分为4 种，如图7 所示．

图7 粘接结构的裂纹形式Fig.7 Cracking behaviors of epoxy resin bonding buttjoints

复杂混合失效是粘接结构最为常见的断裂形式，即由粘接层局部失效扩展至粘接界面和粘接层，如图8 所示．为此，考虑到粘接结构的破坏特点，复杂混合失效时，把粘接界面和粘接层失效与它们之间过渡区的失效进行区分．也就是粘接界面和粘接层失效为临界面，它们之间的过渡区为剪切影响．在CXH模型基础上，为了体现复杂混合失效对多轴疲劳寿命的影响，增加两个方向应变的影响系数，此系数根据实验确定．对CXH 模型进行修改，其公式为

式中：1ξ为最大正应变系数，由粘接界面和粘接层失效面积占粘接面积的比值确定；2ξ为剪切应变系数，由过渡区的面积占粘接面积比值确定．

修正后CXH 模型的预测结果如图9 所示．从图中可以看出，将混合因素影响系数增加后，修正后的模型大大提高了比例和非比例两种路径的多轴疲劳寿命预测的准确度，大部分数据点都落在了2 倍误差范围之内．每个路径只有一个数据点落在2 倍误差线附近下方．从以上的结果来看，粘接结构的疲劳寿命预测，不仅要同时考虑剪切项和拉伸项影响，而且还要考虑粘接结构混合失效的比重因素，这样才能能够更为准确地预测该粘接结构的多轴疲劳寿命．

图8 对接试件多轴疲劳实验的断口Fig.8 Fracture appearance of the butt-joint specimen in a multiaxial fatigue test

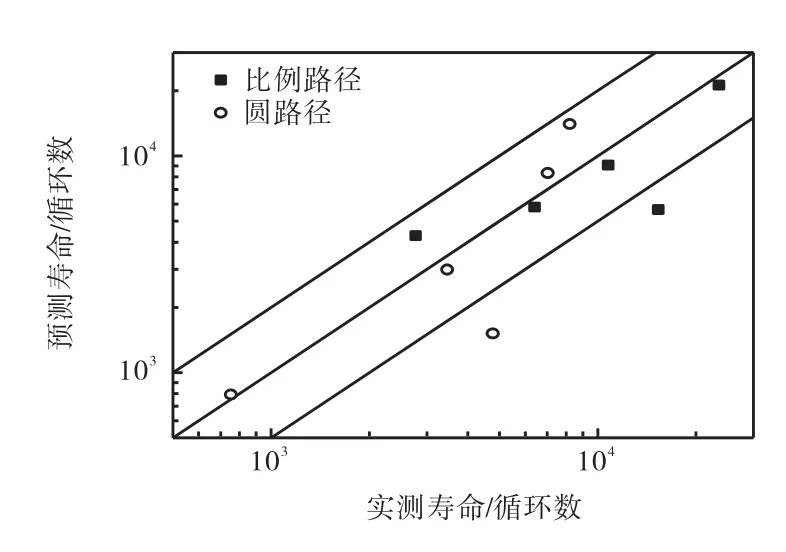
图9 修正CXH模型疲劳寿命预测结果与实验对比Fig.9 Comparison of experimental fatigue lives with predictions using the modified Chen-Xu-Huang model

4 结 语

本文采用环氧树脂胶粘接的中空对接试件，对其进行了单轴拉压、单轴扭转、比例路径和非比例圆路径多轴疲劳实验．根据单轴实验数据，计算出对3 种多轴疲劳寿命预测模型的参数，并采用3 种模型对比例路径和非比例圆路径的疲劳寿命进行预测和分析．结果发现，以最大正应变面为临界面的SWT 寿命预测模型低估了大多数两种加载路径的疲劳寿命，预测结果多数偏于保守；同样，FS 模型以剪应变作为临界面，对比例和非比例两种路径寿命预测过于保守，远远低估了两种路径疲劳寿命．然而，CXH 多轴疲劳寿命预测模型同时考虑拉伸项和剪切项，得到了优于SWT 模型和FS 模型的预测结果，两个路径的寿命数据点都落在2 倍误差线之内和上边界附近，且预测结果较为集中．在CXH 模型基础上，考虑到粘接结构的复杂混合失效特点，增加了混合因素影响系数，修改后的CXH 模型不仅要同时考虑剪切项和拉伸项影响，而且还要考虑粘接结构混合失效的比重因素，修正后的CXH 模型多轴寿命预测模型能够更为准确地预测该粘接结构的多轴疲劳寿命．