计及配网有功无功协调运行优化的SST 规划方法

石季英，乔 文，薛 飞，马 丽，杨文静

(1. 天津大学电气自动化与信息工程学院，天津 300072；2. 国网宁夏电力有限公司电力科学研究院，银川 750001；3. 国网天津东丽供电公司，天津 300300)

随着高比例分布式电源(distributed generation，DG)的接入，配电系统正不断向清洁能源驱动型系统转变．但如何高效利用分布式能源，增强系统的柔性调控能力，是当今电网亟待解决的问题[1]．固态变压器(solid-state transformer，SST)是一种利用全控型电力电子器件实现能量管理和功率控制的变电装置．其交直流多端口设计，可方便DG 的安全接入与灵活组网，同时兼具电压调节、无功补偿和潮流控制等功能，能够有效应对DG 接入带来的诸多问题[2]．

目前针对SST 的研究主要集中在拓扑结构、物理模型和控制方法上，较少有学者关注SST 在配电系统中的运行规划问题．文献[3]在传统配网中建立SST 的稳态运行模型．文献[4]将SST 与有载调压变压器对比，证明了将SST 运用在主动配电网进行无功调节的优越性．文献[5-7]忽略SST 的控制方法，针对其外特性，构建了基于SST 的无功优化模型．文献[8]提出一种以电压偏移最小为目标的功率-电压协调控制方法．文献[9-11]考虑SST 协调配网有功运行优化问题，提出含SST 的交直流系统调度优化方法．

以上研究表明，借助SST 的潮流调节、无功补偿等能力有助于提升配网的运行控制潜力，但目前只涉及SST 与系统有功资源的协调运行．有别于输电网，配网线路的有功和无功耦合性较强[12]，忽略无功运行，只对SST 参与协调配网单方面有功协调运行分析，是不够全面的．充分协调SST 参与配网有功无功运行优化，一方面，统筹系统的有功无功协调运行，可更精准地对SST 进行运行调控，提高系统的柔性调节能力；另一方面，协调SST 的电能调节作用，进一步对系统的有功无功资源综合调配，可以实现运行效益的最大化．

此外，较高的投资成本[2]也使得SST 在配网中的合理规划显得十分必要．然而目前只有文献[13]考虑了SST 的规划研究，其忽略系统运行优化影响，提出一种单层规划模型，证明SST 的规划有益于改善线路过载和电压过低情况．但该模型完全忽略了SST高成本带来的经济影响，无法为SST 的实际工程规划提供经济性理论指导．同时没有考虑规划结果与运行优化之间的耦合关系，单层求解的规划模型也限制了规划结果的合理性．

本文计及SST 协调配网有功无功运行优化，提出一种充分考虑模拟运行结果的SST 规划方法．研究SST 稳态数学模型，提出一种考虑负荷与分布式电源时序性的参数控制方法．充分协调配电网有功无功资源，研究了SST 协调配电网有功无功资源运行优化策略．考虑SST 投资成本、环境效益和配电网运行成本，构建了融合配网有功无功时序运行优化的SST 双层规划模型，采用改进的主从式差分入侵杂草混合算法对运行层与规划层解耦求解，计及协调有功无功运行对SST 规划的积极作用，促进SST 规划方案的合理性．

1 固态变压器的稳态模型

理想的SST 具有多个不同电压等级的交/直流端口，其中交流端口主要连接交流子网、交流微网、交流负荷和交流型分布式电源；直流端口主要连接直流子网、直流微网、直流负荷和直流型分布式电源．与传统变压器相比，SST 增加直流端口设计，丰富了系统组网形式，同时在无功功率补偿与谐波治理、故障隔离与环保运行等方面具有很大优势．针对多场景下交流负荷、直流分布式电源和直流储能系统的接入情况，本文以SST 在双交流系统及交直流系统连接模式下，研究其在配网中的优化配置．理想多端口SST 的稳态数学模型如图1所示．

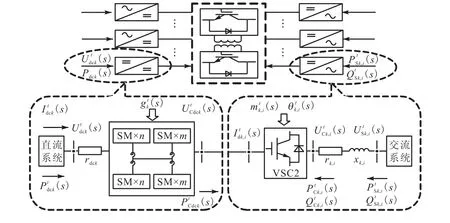
图1 SST的稳态数学模型Fig.1 Steady-state mathematical model of SST

设交流/直流端口共计k个，其中各端口的功率方程分别为

式中：i为配网节点；s为优化场景；t为优化时段；k为SST 的端口数(文中1 表示中压交流端口，2 表示低压交流或低压直流端口)；rk,i和xk,i分别为换流器的等效电阻和电抗；αk,i＝arctan(rk,i/xk,i)；Yk,i=和分别为端口与系统交换的有功和无功功率；为交流端口侧连接系统的电压幅值；和分别为两侧VSC吸收的有功和无功功率；为交流端口侧的端口电压幅值；为SST 交流端口VSC 的调制角；为直流端口侧转换器一次侧的电压赋值；为直流端口侧转换器与SST 的交换功率；为直流端口侧的电压赋值；为直流端口侧的电流赋值；为直流端口转换器的直流电压比；rdck为直流端口损耗的等效电阻；Ф和Ψ分别为直流和交流端口集．

为保证运行稳定，在SST 中压交流端口采取定直流电压控制(恒定)，低压交流端口或低压直流端口采取电压控制(恒定或恒定)，即控制低压交流或直流侧电压的相位与赋值．低压交流端口输入的有功和无功功率由交流负荷(和决定，低压直流端口输入的有功功率由多场景时序直流分布式电源或储能系统决定在中压交流端口侧，SST 可以通过控制中压交流端口的有功和无功出力，实现系统的无功调节与潮流控制，在低压交流/低压直流端口侧，SST 可以通过控制低压端口侧的输出电压，实现低压系统的电压控制．

对于SST连接中压交流与低压交流系统的接入方式，由PWM 调制原理，可得

将式(8)代入式(1)～(3)，SST 低压交流端口侧的有功和无功功率表达式可以转换为

由式(9)和式(10)对和进行求解得

由式(11)和式(12)对进行求解得

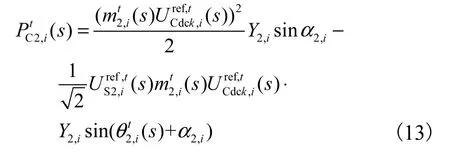
将式(13)代入功率平衡方程式(7)中，得到的函数表达式为

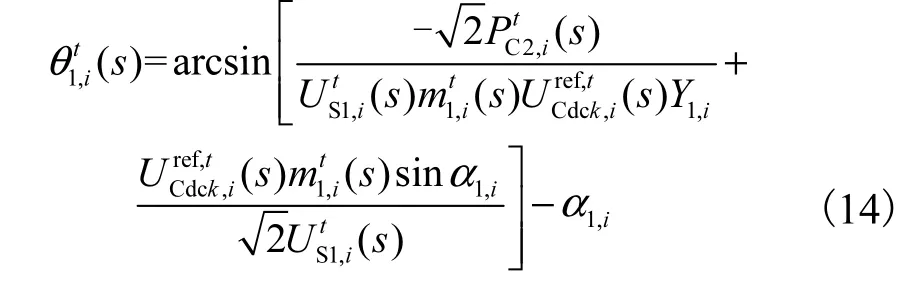
联立式(1)、(2)、(8)和(14)，得到SST 中压交流端口侧有功和无功功率的函数表达形式为

对于SST连接中压交流与低压交流系统的接入方式，与恒定，只需控制调制比即可进行SST 中压交流端口侧与系统交换的有功和无功功率的时序调节．

对于SST连接中压交流与低压直流系统的接入方式，联立式(5)～(7)可得

将式(17)代入式(3)和式(8)，得到的函数表达式为

联立式(1)、(2)、(8)和(18)得到SST 中压交流端口侧有功和无功功率的函数表达形式为

同理，对于SST连接中压交流与低压直流系统的接入方式，与恒定，只需控制调制比即可进行SST 中压交流端口侧与系统交换的有功和无功功率的时序调节．

为保证稳定运行，设置调制参数约束和功率约束方程[14]为

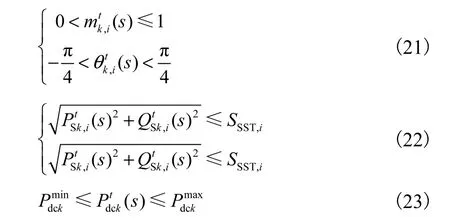
式中：是SST 的视在功率；和分别为SST 直流端口的端口功率上、下线约束．

2 计及有功无功协调运行的SST规划方法

2.1 上层规划模型

本文所提的SST 规划方法既要确定SST 的安装位置与容量，又要计算多时段各场景下配电网有功无功资源的最优运行状态．

上层规划模型以年综合费用最小为目标函数，包括 SST 的等年值投资成本(年运维成本环境效益和配电网年运行成本(Cope)分别为

式中：CLoss、CGrid和Cξ分别为网损成本、主网购电成本和设备运行成本，包括微型燃气轮机(MTG)、风力机组(WTG)、储能、需求响应和电容器组；T为时间总数；N为场景总数；ΩSST为SST 的候选节点集；d为贴现率；p ( s) 为场景概率；y为SST 的经济使用年限；cSST为SST 的单位容量投资成本；η和γ分别为SST 的年运维系数和环境效益系数，环境效益由SST减少传统变压器油的污染产生，取负值；λi为传统变压器油转换系数；βς为变压器油的环境效益转换系数；ς为环境效益类别，以《排污费征收使用管理条例》为基准核算，包括标准煤能耗、水质、土壤、固体物和大气污染；eς为能耗排污价格[15]．

SST 的安装容量需满足约束

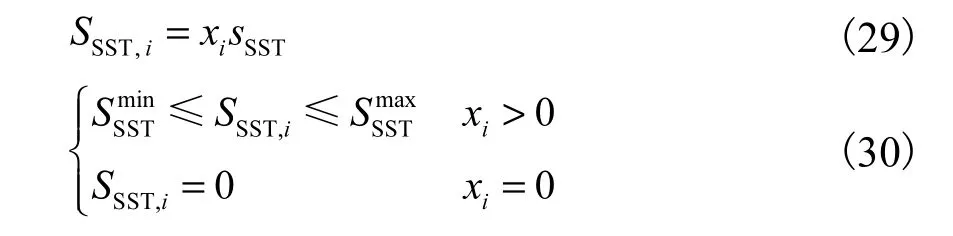
式中：sSST为单位容量SST 的安装容量；xi为安装SST 单位容量的数量，用非负整数表示；SSST,i表示安装SST 的容量；和分别为安装容量上、下限.

2.2 下层规划模型

下层模型基于上层传递的SST 规划配置方案，优化系统有功无功资源的协调运行，以配电网日运行成本最小为目标，即

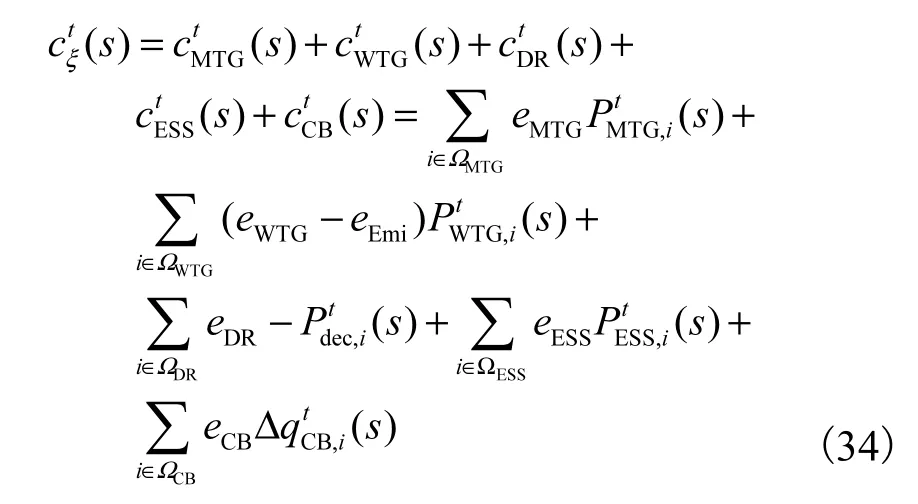
式中：e、eGrid、eMTG、eWTG、eEmi、eDR、eESS和eCB分别为售电价格、主网购电价格、MTG 发电价格、WTG发电价格、传统火电排放价格、需求响应运行价格、储能运行价格和电容器投切价格；ΩBrence、ΩMTG、ΩWTG、ΩDR、ΩESS和ΩCB分别为配网支路集、MTG、WTG、柔性负荷、储能和电容器组的安装节点集；和分别为网损量、主网购电量、MTG 和WTG 的有功出力及需求响应减少电量；为电容器组投切变量；为支路电流赋值；Rij为支路电阻．

下层除要考虑SST 的运行约束式(21)～(23)，还需考虑如下约束．

(1) 节点功率平衡约束为

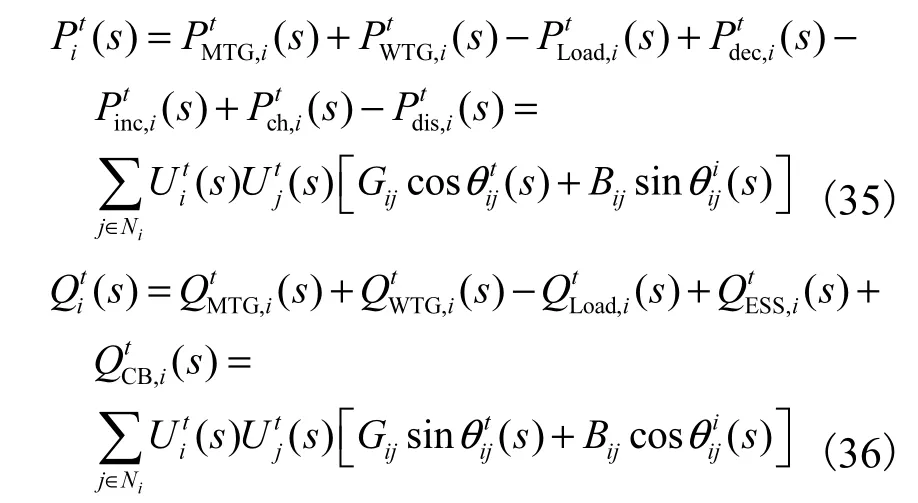
(2) 配电网运行约束为

(3) MTG 运行约束为

(4) WTG 运行约束为

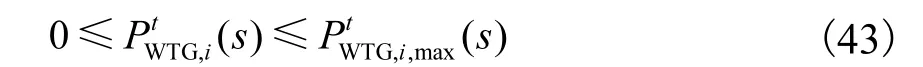
(5) 需求响应约束为

(6) 储能运行约束

(7) 电容器组运行约束为

2.3 主从式差分入侵杂草混合算法

差分入侵杂草算法(DEIWO)既结合入侵杂草算法(IWO)结构简单和鲁棒性强的优点，又利用差分进化算法(DE)克服陷入局部最优，可用于非线性多元优化问题的求解[16]．本文以待安装SST 的节点位置和容量作为控制变量进行上层优化，下层根据上层选定的配置方案进行配网有功无功协调运行最优求解，上下层迭代求解，得到最优运行结果下的最优规划方案．为缩短计算时间，采用主从式并行计算架构，主处理器负责双层模型的整体流程，先对上层杂草初始化，再分别发送给两个子处理器，在不同的场景下进行下层运行最优求解，并将下层结果返回到上层进行年综合费用的计算，完成上层迭代优化．具体求解流程如图2 所示．

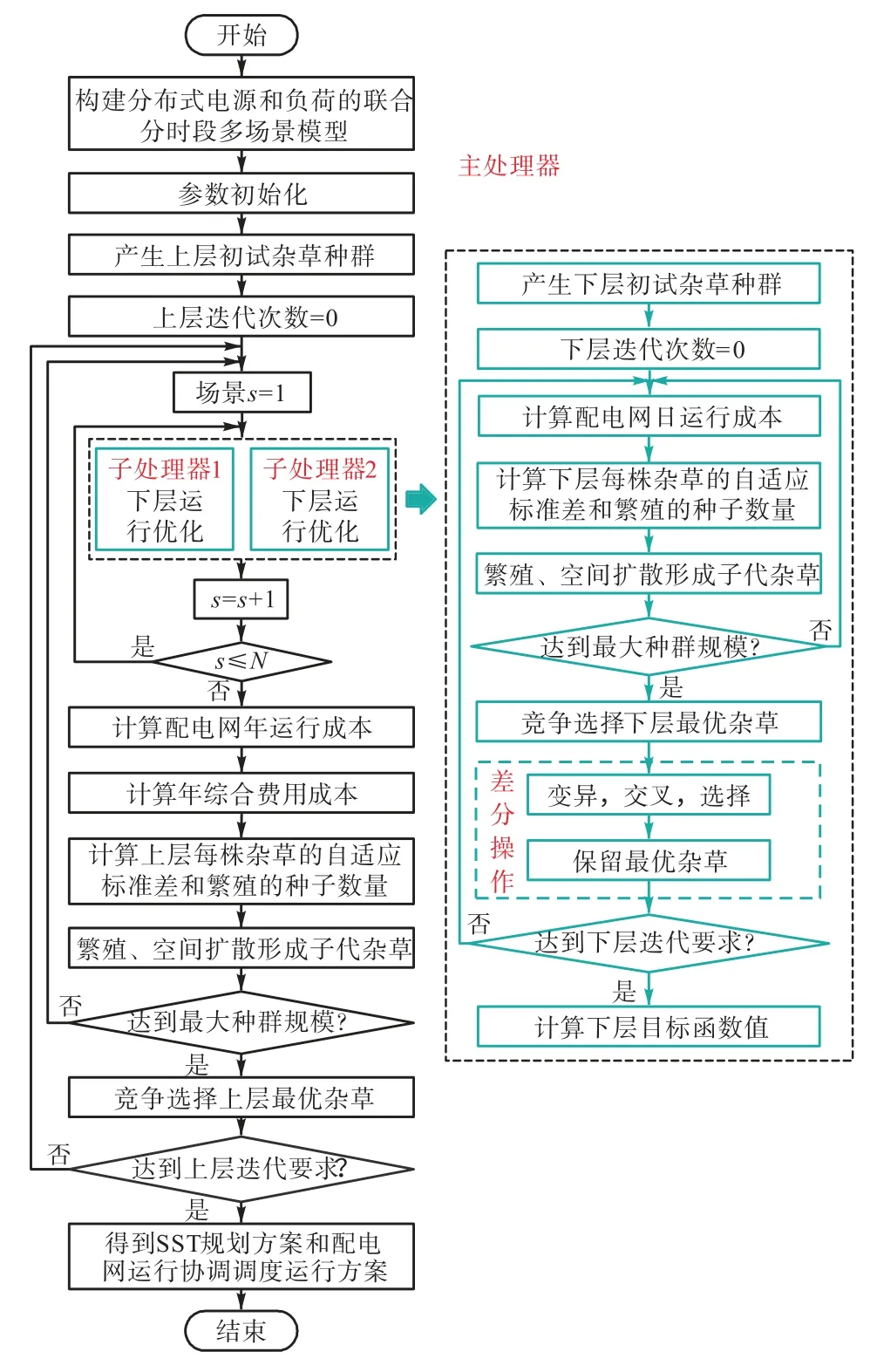
图2 SST规划流程Fig.2 Flow chart of planning model for SST

3 算例仿真与分析

3.1 算例概况与参数设计

采用改进的IEEE33 节点算例对所建双层规划模型进行分析验证，如图3 所示．系统接入的WTG、MTG 和储能系统的基本配置参数如表1 所示．电容器组安装在节点10 和节点27 处，其调节容量为200 kvar，调节步长为 10 kvar．此外，系统网络和WTG 的相关参数详见文献[17]，MTG、储能系统、需求响应和分时电价的相关参数详见文献[18]，电容器组运行参数详见文献[19]．SST 相关参数如表2 所示[2,9,15]，选择中低压交流双端口电压变比为10 kV/400 V，选择中压交流低压-直流双端口电压变比为10 kV/750 V，以4、7、12、14、16、24、28、29、30、32和33 节点作为SST 的待选位置．假设各节点风速环境相同，根据典型日[17]风速情况，采用拉丁超立方抽样和后向场景消减法，建立风机出力时序多场景模型，将各时段划分为5 个场景，如图4 所示．负荷运行曲线根据典型日历史数据得到[19]．算例在Matlab R2016a 环境求解，主从式DEIWO 求解上下层规划模型的最大迭代数均取值为50，算法其余参数详见文献[16，20]．

图3 修改的IEEE 33节点配电系统Fig.3 Modified IEEE 33-node distribution system

表1 系统配置相关参数Tab.1 Related parameters of system configuration

表2 固态变压器的相关参数Tab.2 Related parameters of SST

图4 风电概率场景Fig.4 Schemes of WTG

3.2 规划结果分析

设置4 种规划方案如下.

方案1考虑SST 协调配电网单有功资源的运行优化，对SST 进行双层规划．

表3 规划结果与成本对比Tab.3 Comparison of planning results

方案2考虑SST 协调配电网单无功资源的运行优化，对SST 进行双层规划．

方案3综合考虑SST 协调配电网有功无功资源的运行优化，对SST 进行单层规划．

方案4综合考虑SST 协调配电网有功无功资源的运行优化，对SST 进行双层规划．

规划结果和成本对比如表3 和表4 所示，表中所有成本均为等年率值．

3.2.1 SST 协调有功无功运行分析

对比方案1、2 和4 的规划结果和各项成本，重点分析考虑SST 协调配电网有功无功综合运行优化对规划模型的影响．

由表3 可知：①方案4 的年综合费用比方案1 和2 分别减少了91.1 k$和21.8 k$，说明综合考虑SST协调配网有功无功优化运行提高了规划结果的经济性；②相较于方案1 和2，方案4 的配网年运行成本分别减少了78.5 k$和28.0 k$，说明考虑SST 协调配网有功无功优化运行，可充分协调SST 参与配网有功无功资源调度运行，减少配网运行成本，并积极作用于SST 的规划结果，降低系统整体经济成本；③方案1 中SST 的投资成本比方案2 和4 分别提高3 倍和1 倍，其年综合费用分别提高69.3 k$和91.1 k$，说明仅依靠SST 在配网中的无功调节能力，在SST 投资成本较高的现状下，会导致配电网综合经济成本较高；④规划结果中，SST 接入系统的连接方式的主要选择为中低压双交流系统的连接方式(代替传统配电变压器)，其与中压交流与低压直流系统的连接方式(代替AC-DC 转换器)相比，所实现的无功调节与经济效益优势更突出．

由表4 可知：①方案1 中的网损成本小于方案2、4，说明SST 在配电网中具有较强的无功调节能力，可有效减少系统网损，提高运行稳定性；②方案1、4 的主网购电成本均小于方案2，这是因为方案2忽略了系统中DG、储能系统与柔性负荷的有功调节，过度依靠主网购电维持系统有功所导致；③方案4 的总运行成本优于方案1，说明充分协调系统有功无功资源运行优化，有助于改善系统运行经济性，从而得到更优的规划方案．

表4 运行成本结果对比Tab.4 Comparison of operating cost results k$

方案1、2 和4 的日运行成本如图5 所示，对比考虑单有功/单无功运行方案，方案4 综合协调配网有功无功资源在峰时段的运行成本优势最为明显，说明SST 协调配网有功无功运行可更好应对DG 和负荷的波动性，降低系统运行经济成本．

选取运行日风机出力第3 场景为例，方案1 在14 节点、方案2 在28 节点及方案3 在30 节点的SST 发出的无功功率如图6 所示．由图可知，方案4发出的无功功率最少，方案1 最多，说明SST 参与有功无功协调运行，可提高系统的潮流控制和电压调节能力，降低SST 的无功补偿压力．

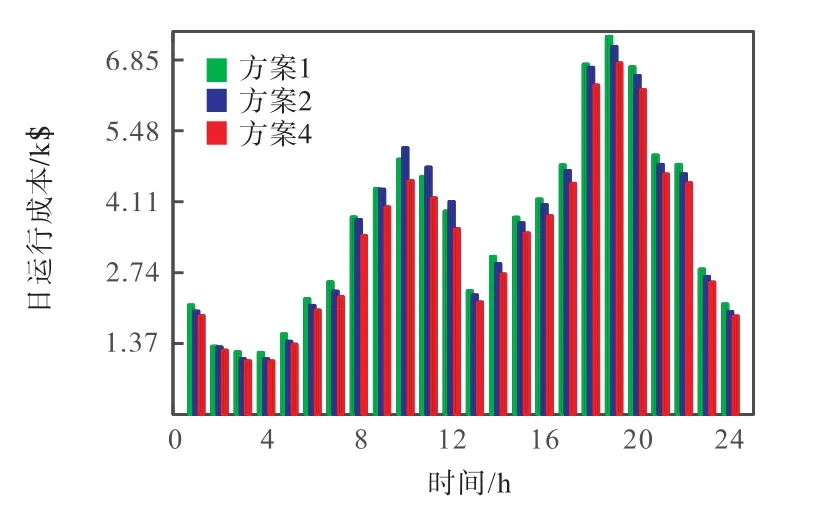
图5 日运行成本Fig.5 Daily operating costs

图6 SST发出的无功功率Fig.6 Reactive power injection of SSTs

为验证SST 协调配电网有功无功优化运行对电压质量的改善情况，以峰(19：00—20：00)、平(14：00—15：00)和谷(02：00—03：00)时段在第1 场景的运行结果为例，系统节点电压的分布情况如图7 所示．选取电压分布最低的18 节点，其各时段的电压偏差期望如图8 所示．

从图7 可以看出，SST 联合系统有功无功运行优化，在峰、平及谷时均可改善电压偏差情况，有效缓解DG 和负荷的波动接入带来的冲击，其中峰时的优化效果最为突出．值得关注的是，方案1 中SST 的规划配置数量最多，其电压运行偏差最小，证明了SST较强的无功调节能力．从图8 可以看出，方案1 与方案4 的电压幅值波动情况较方案2 得到改善，且方案1 与方案2 的最大偏差相差较小，说明在考虑经济规划成本的情况下，SST 充分协调系统有功无功运行优化可缩小电压偏差，改善供电质量，减少系统网损，进而积极作用于SST 的规划结果．

3.2.2 运行-规划双层解耦模型分析

对比原系统、方案3 和4 的规划结果与各项成本，重点分析运行层与规划层解耦模型对规划结果的影响．

图7 系统电压分布Fig.7 Nodal voltage profile

图8 18节点的电压偏差Fig.8 Voltage deviation of node 18

由表3 可知：①方案4 的年综合成本比原系统减少了54.2 k$，方案3 比之减少了1.3 k$，表明受限于SST 的高昂投资成本，只有合理的SST 规划方案才能充分实现系统整体的经济性能优化；②方案3 和方案4 的配电网年运行成本比原系统减少了13.9 k$和106.6 k$，说明将SST 的无功补偿和潮流调节能力应用于配网协调运行，可提升系统的运行经济性能；③方案4 比方案3 的年综合费用减少了92.7 k$，表明本文模型充分考虑下层协调运行与上层规划配置的相互作用，较单层规划模型，更益于实现经济合理的规划结果．

由表4 可知：①方案3 比方案4 的WTG 年运行成本增加了17.3 k$，说明双层规划模型相较于单层模型有助于增强系统的调节能力，提高清洁能源的消纳率．②与原系统相比，方案3 和方案4 的网损成本分别减少了45.6 k$和46.5 k$，说明SST 的规划和应用有助于调节系统无功，改善系统电压偏差；③方案3 与方案4 相比，除了系统网损和WTG 的年运行成本，其余运行成本明显增高，导致总运行成本升高，说明单层规划模型将规划结果与运行结果统一求解，忽略规划与运行的相互影响，不利于运行结果的充分寻优，从而限制规划结果的合理性．

方案3、方案4 和原方案的日运行成本如图9 所示，虽然方案3 和方案4 的总运行成本均比原方案减少，但方案3 在部分时段的运行成本接近甚至超过原方案，说明运行优化结果并未能实现最优，而方案4在各时段运行成本均得到了降低，进一步说明在双层模型中将规划层与运行层解耦优化，运行层寻优能力比单层模型更强，更适合规划结果的求解．

图9 单双层规化模型日运行成本对比Fig.9 Daily operating costs of single and bi-level planning models

为比较双层规划与单层规划模型中SST 的无功调节、改善电压偏差能力，以峰(19：00—20：00)、平(14：00—15：00)和谷(04：00—05：00)时段在第1 场景运行结果为例，节点电压分布如图10 所示．系统各时段的电压最小值如图11 所示．

图10 单双层规化模型系统电压分布对比Fig.10 Nodal voltage profile of single and bi-level planning models

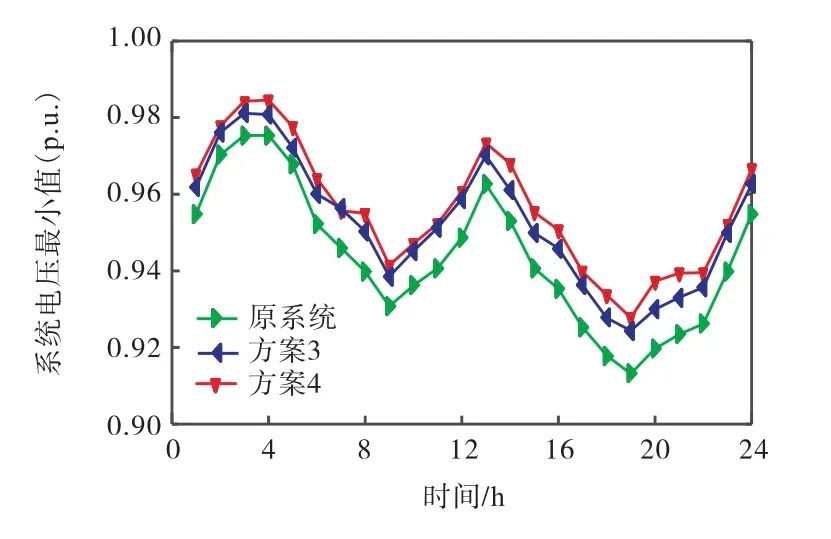
图11 系统电压最小值Fig.11 Minimum system voltage

从图10 可以看出，在峰、平及谷时段，SST 的规划运行均可实现电压偏差的改善，有效缓解系统中DG 和负荷的接入带来的冲击．且双层规划模型中电压波动最小，说明双层模型中解耦优化规划层与运行层，可实现更优的前期运行优化，从而得到更合理的规划结果．从图11 可以看出，方案4 的电压幅值波动情况得到了改善，电压偏差总和相较原系统和方案3 分别减少了25%和18%．

4 结 论

本文融合SST 的运行特性、负荷及分布式电源的不确定性，研究了SST 在中低压双交流与中低压交直流系统连接模式下的时序稳态控制方法．计及SST 协调配电网有功无功运行优化，考虑SST 的投资成本、环境效益和配网运行成本，建立了融合运行优化结果的SST 统筹规划模型．通过算例得到的结论如下．

(1) 本文方法可充分考虑协调主动配电网有功无功运行对SST 规划的影响，相较于考虑单方面有功/无功运行和单层的规划方法，其在运行经济性与安全性方面优势更突出，更易获得合理的SST 规划方案．

(2) 与中压交流-低压直流系统的连接方式相比，SST 在中低压双交流系统的连接方式下，其无功调节能力与经济效益更具优势．

此外，基于多端口灵活设计的SST 可选择不同的接入节点和控制模式，本文仅针对SST 在中低压系统连接方式下的无功补偿和潮流调节能力进行配置规划．如何在规划模型中充分考虑配网复杂组网形式和更多柔性控制需求将是今后研究的方向．