规则波中船舶Froude-Krylov 力的解析积分计算
张 腾,任俊生,张秀凤,梅天龙
(1. 大连海事大学航海学院,大连 116026;2. 上海交通大学船舶海洋与建筑工程学院,上海 200240)
船舶航行在大洋中时时刻刻遭受波浪的作用,船舶在波浪中的大幅度摇荡运动也会对船体结构造成破坏,从而大大降低船舶的适航性,更为严重的会导致海难的发生.因此,准确计算船体所受的波浪作用力对船舶操作、设计及运营显得尤为重要.
自20 世纪50 年代以来,船舶在波浪中所受的Froude-Krylov 力及运动的研究取得了一定的进展,主要体现在从无限水深到有限水深及从数值计算到解析计算方法的转变.在无限水深范畴内,Korvin-Kroukovsky 等[1]基于二维理论,采用切片法将船体离散成若干等截面的切片,数值计算出船舶各个横剖面由于入射波作用引起的F-K 力,沿船长方向积分可得到总的F-K 力,但其并未考虑到由入射波引起的绕射力.Salvesen 等[2]进一步提出了STF 法,该理论有效地考虑由入射波引起的绕射力对船体的作用,其运动预报精度有了较大提高.基于三维范畴内,Beck等[3]及孙葳等[4]将船体平均湿表面离散成一系列四边形平面面元,F-K 力可由高斯积分定理在平面面元上进行直接积分得到.邹元杰等[5]基于“高频低速”假定对零航速格林函数进行航速修正,并分析了波浪中行驶船舶在不同波长处所受的水动力及F-K 力对船舶运动的影响.
以上文献中F-K 力计算都是基于无限水深及数值积分进行的,实际上,水深对船舶运动具有很大的影响,比如船舶破损事故经常在有限水深海域发生,因此F-K 力的计算需要考虑水深的影响是必不可少的.在有限水深下,基于二维理论,贺五洲等[6]采用切片法预报船舶所受到的F-K 力、辐射力及绕射力.基于三维频域理论,冯乾栋等[7]基于有限水深三维频域格林函数,对有限水深中的破损船舶波浪载荷进行数值计算.在三维时域内,刘昌凤[8]采用数值积分方法计算船舶在有限水深及无限水深下所受到的F-K 力,并基于三维时域Green 函数[9],成功地预报了船舶在规则波中的运动.上述不管有限水深还是无限水深中F-K 力的计算,都是基于数值积分方法,对于具有强烈波动性的F-K 力的计算,即使将船体划分大量的面元,仍然存在数值积分误差.Rodrigues等[10]采用解析压力积分表达式对无限水深以正弦表达式形式的规则入射波产生的F-K 力进行精确计算,其船体表面网格划分与计算水动力相同的粗网格相同,精度却毫无损失,避免了数值积分计算F-K 力产生的数值误差.但是该研究进行F-K 力解析积分计算时仅仅考虑无限水深这种特殊的情形,并没有将水深因素考虑进去,在近海处,由有限水深带来的浅水效应对F-K 力的计算有较大的影响.
为避免数值积分方法计算F-K 力带来的误差及减少船体表面面元划分数量,并将流域水深因素考虑进去,基于格林定理,本文详细推导了任意水深下FK 力在四边形平面面元上的解析积分表达式.研究了流域水深在不同入射波浪向角及波长下对作用在WigleyⅠ型船[11]船体上的F-K 力的影响,并进一步基于三维时域Green 函数建立了船舶任意水深下的波浪激励力计算模型.最后,对迎浪航行在规则波中WigleyⅠ船舶受到的波浪激励力进行预报.
1 数学模型的建立
如图1 所示,参考坐标系Oxyz 固定在以速度U前进的船体上,原点O 为船舶中点,Oxy 与静水面重合,Ox轴正方向指向船首,Oy 轴正方向指向船舶左舷,Oz轴正方向垂直向上.面元局部坐标系O′x′yz′ ′的原点O′为面元几何中心,O′xy′ ′与四边形面元平面重合,O z′ ′轴正向垂直于四边形平面面元,且指向船体内部.面元局部坐标坐标与参考坐标系Oxyz 坐标 r ( x , y ,z)的转换式为
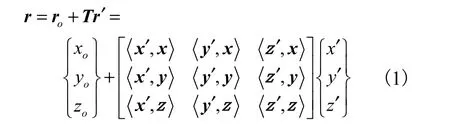
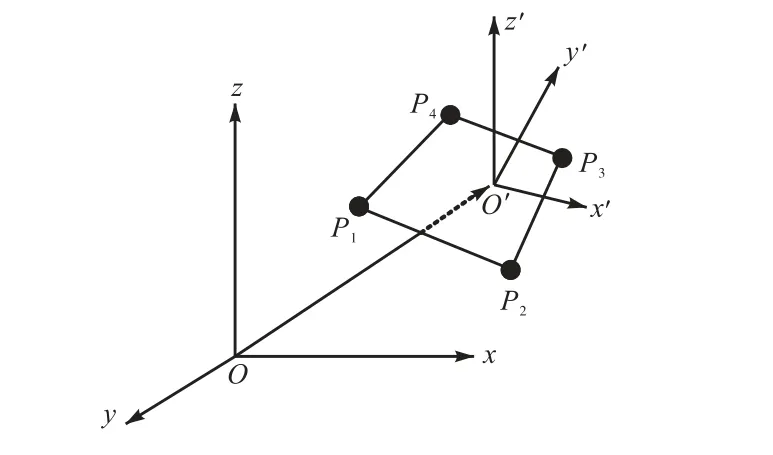
图1 参考坐标系与面元坐标系Fig.1 Reference coordinate system and panel coordinate system
1.1 F-K力的解析积分表达式推导
假定流体不可压缩、无黏性,且流动是无旋的,不考虑流体表面张力效应.水深为d的入射波速度势及入射波波高在参考坐标系下的表达式分别为
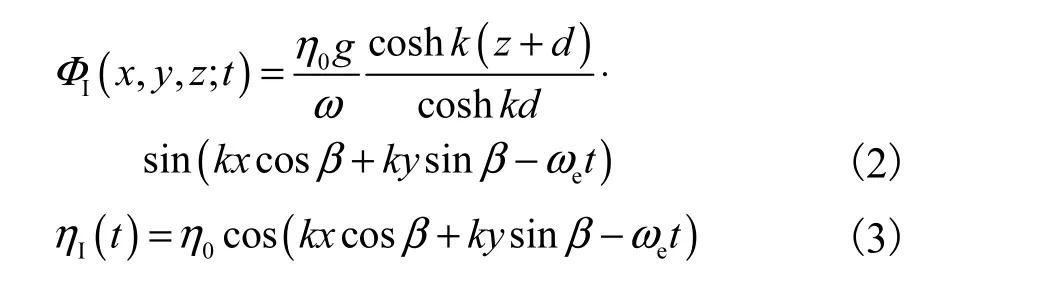
式中:0η为入射波波幅;g为重力加速度;ω为入射波原频率;k =ω2g 为波数;β为浪向角,其传播方向与Ox轴正方向的夹角,迎浪为为遭遇频率.
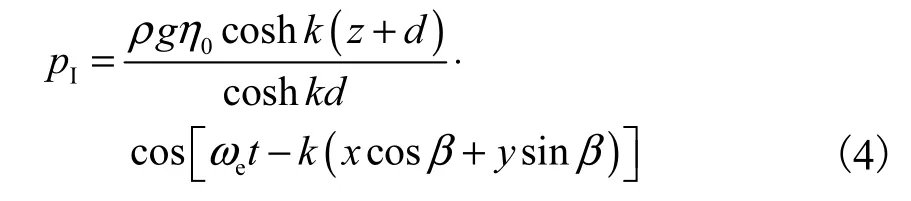
式中ρ为流体密度.
将船体湿表面处理为N块四边形平面面元,则第i块面元上的入射波压力积分为
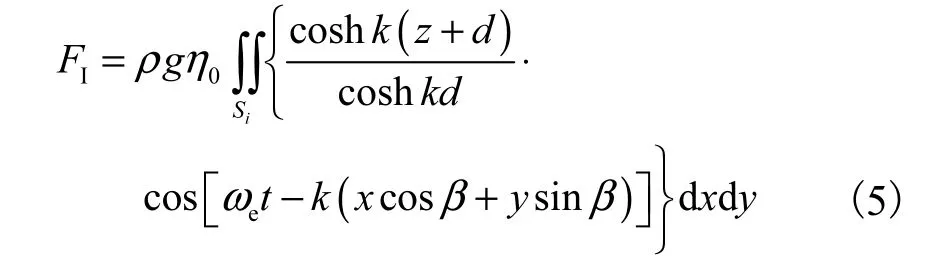
式中Si为第i 块面元面积.
经过推导,则IF可写为
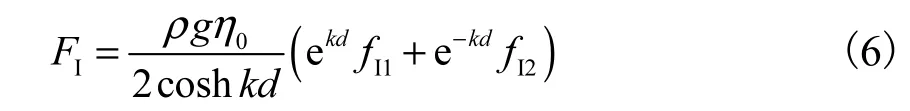
式中 fI1及 fI2可分别写为

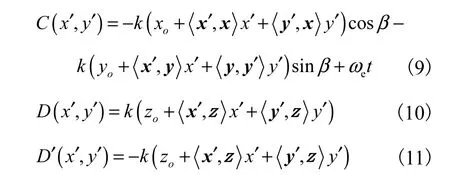
第i块四边形面元上第j条边在面元坐标系内可以参数化得

则第i块面元第j条边上的C、D 及D′ 关于参数α的表达式分别为
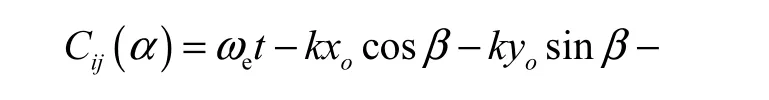
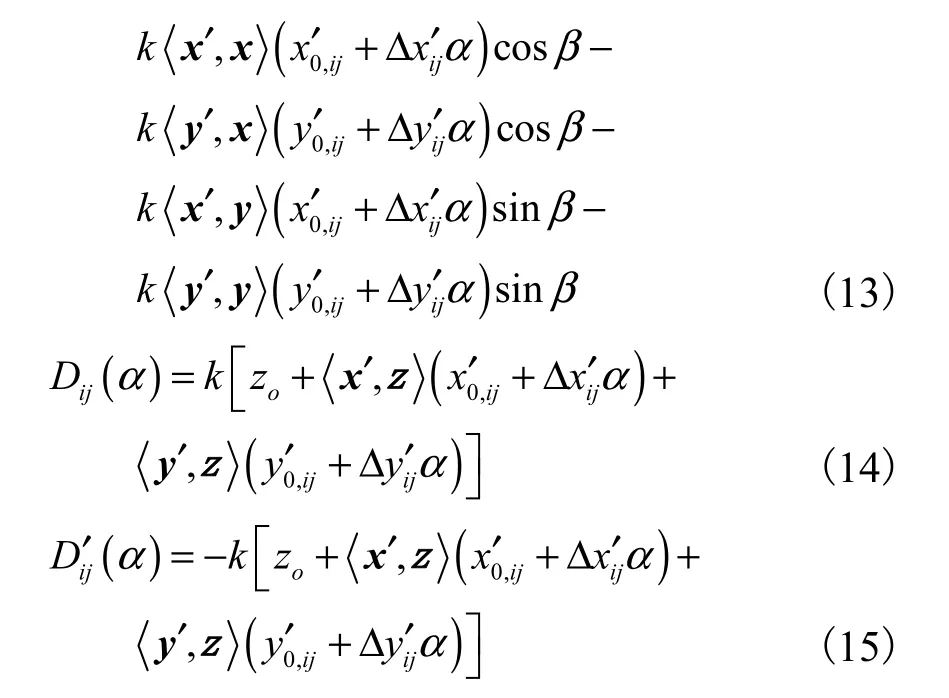
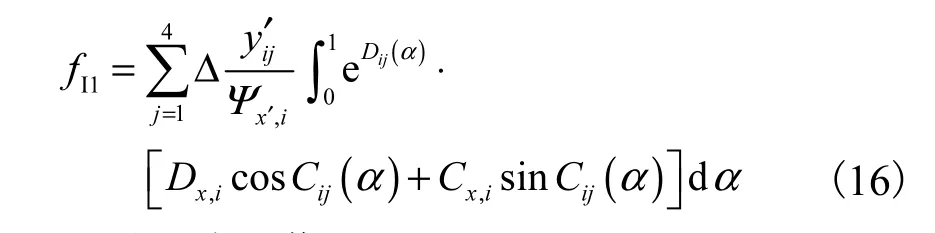
fI1可进一步写作
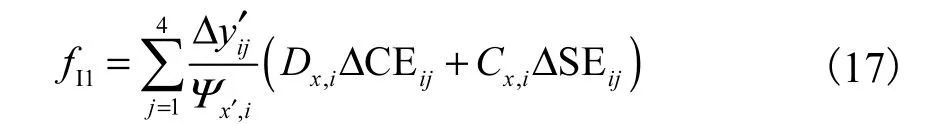
式中 ΔC Eij和 ΔS Eij可表示为
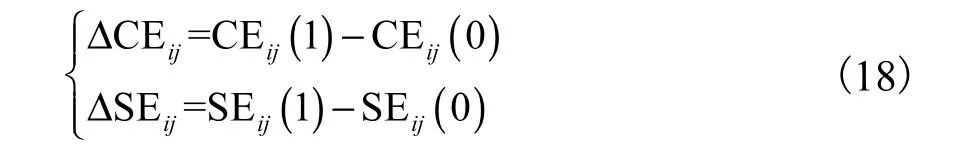
式中SEij及CEij可表示为
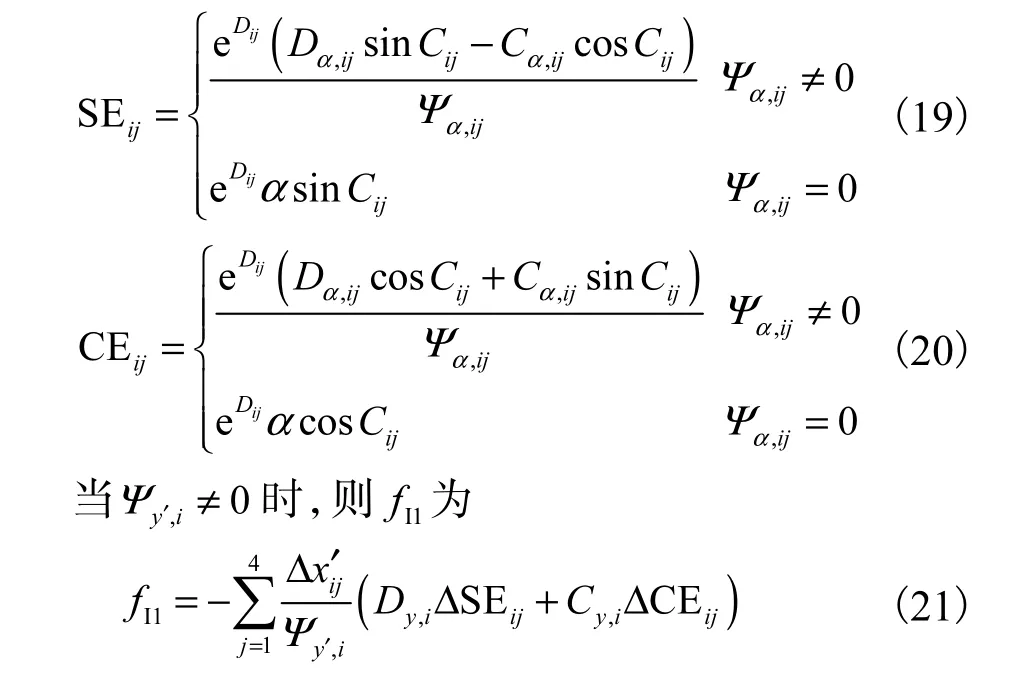
同理,可以采用相同方法求取fI2.最终将fI1及代入式(6),解得入射波压力积分IF.
同理,可以采用解析积分表达式求解F-K 力及力矩.值得注意,当水深 d→∞时,此时IF可以表示为

注意:式(22)为IF为无限水深时F-K 力的解析积分表达式,相对于有限水深F-K 力的解析表达式(6),式(22)中不包含水深d 的影响.
1.2 绕射问题求解
在Oxyz 参考坐标下的入射波遇到船体反射产生绕射势DΦ,其满足如下条件:
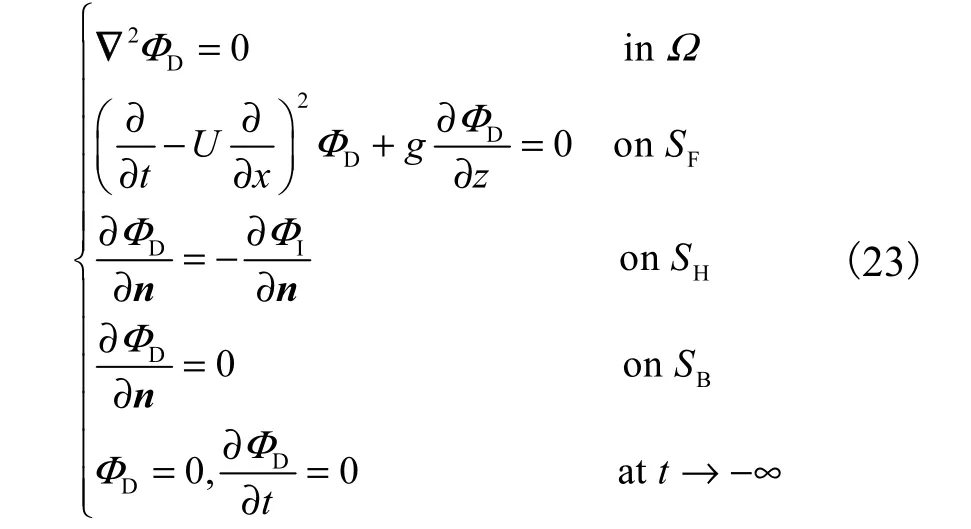
式中:Ω为流域;SF为自由液面;SH为船体平均湿表面;SB为水底面积;n 为单位法向量,指向流域外部.令分别代表船舶纵荡、横荡、垂荡、横摇、纵摇及首摇.
时域格林函数用于求解满足绕射势DΦ边界方程
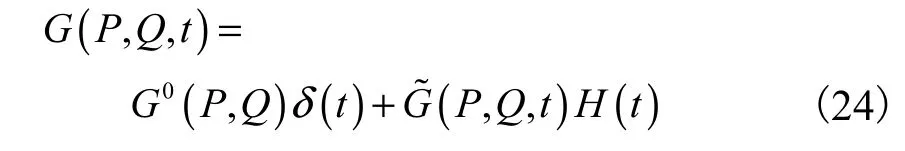


G0与的数值求解可由文献[9,12-13]所得,其绕射势ΦD满足的边界积分方程[8]为
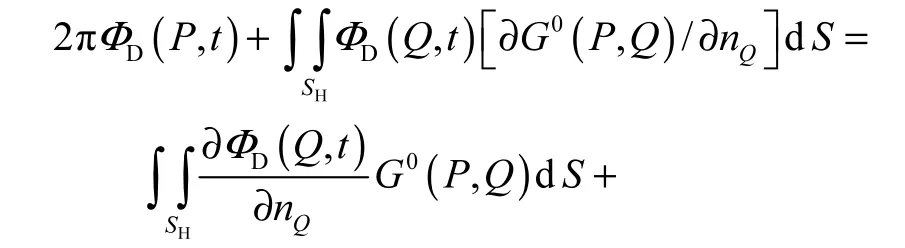
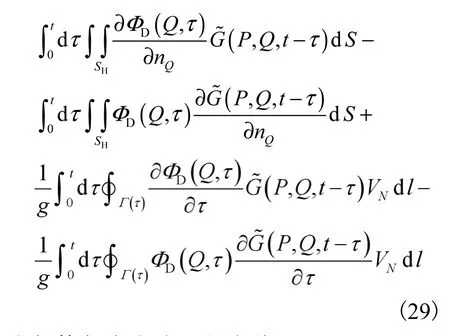
式中:Γ为船体与自由液面的交线;为垂直水线指向船体内部的单位法向量.
采用常数面元法求解式(29),最终求解出绕射势
DΦ,则由绕射势产生的压力 pD为

则i运动模态上的绕射力FDi为

i模态上的频域波浪激励力 Fwi可由 FDi与 FIi合力经过傅里叶变换得到[8].
完成建模工作后,有必要对Rodrigues 方法[10]与本文方法做一个比较,如表1 所示.
如表1 所示,本文方法相对于Rodrigues 方法,适用范围更为广泛,主要体现在:①本文采用解析积分方法计算任意水深下的F-K 力,而Rodrigues 采用解析积分方法只计算无限水深下的F-K 力;②本文采用直接时域方法计算流体扰动力,可以有效避免采用间接时域方法在高频处的数值误差;③本文入射波波高以余弦形式表示,而Rodrigues 方法以正弦形式表示,最终两者F-K 力解析积分表达式不仅体现在有无水深项的不同,还体现在式(17)及式(21)括号项中表达式的不同.
2 数值模拟与结果分析
2.1 面元上F-K力的解析积分计算验证与分析
首先选取1 块1 m×1 m 的正方形面元进行研究,其4 个顶点坐标在参考坐标系中依次为(-0.5,0,-1)、(0.5,0,-1)、(0.5,0,1)和(-0.5,0,0).该面元前进速度为U =1 m/s,入射波波长λ=5 m,波幅0η=0.1 m,水深d =6 m.在t=3 s 时刻,对浪向角β为及在该面元上F-K 力由压力积分解析表达式分别求得为446.637 N、-88.462 N(保留到0.001 N).对面元上FK 力采用高斯数值积分进行计算,并进一步对面元进行如图2 的剖分,直到与解析解求得的结果相同为止.
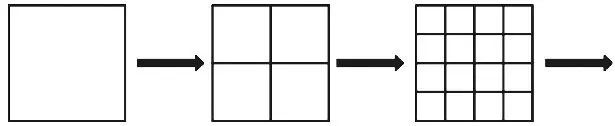
图2 面元剖分示意Fig.2 Panel subdivision schematic
由表2 可知,当划分次数为3 时,数值积分解与解析积分解具有相同的精度,此时面元被划分为64个子面元,数值积分所需要的面元数目远远大于解析积分.对于形状比较规则的箱形体船,比如驳船[10],需要6 块面元即可求出准确的F-K 力值,极大地提高了计算效率.
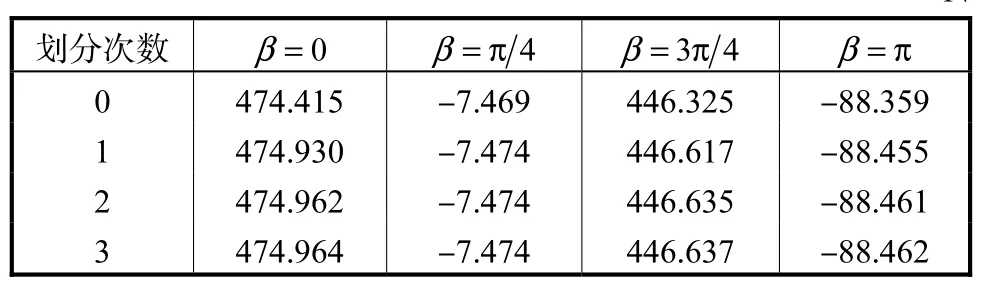
表2 t=3 s面元上F-K压力积分值Tab.2 Values of F-K pressure integration on the panels at t=3 s N
2.2 船体F-K力的计算与分析
本文采用WigleyⅠ型船验证数学模型的可靠性与准确性,其主要参数如表3 所示.并将船体平均吃水一下的船体划分为80×4 个面元,如图3 所示.

表3 WigleyⅠ型船主尺度Tab.3 Main particulars of Wigley Ⅰ hull

图3 Wigley Ⅰ型船体面元划分Fig.3 Panel distribution for Wigley Ⅰ hull
由图4 和图5 可得,“数值积分”与“解析积分”的F-K 力时间历程完全重合,从而验证了本文开发的F-K 力解析积分算法的可靠性.
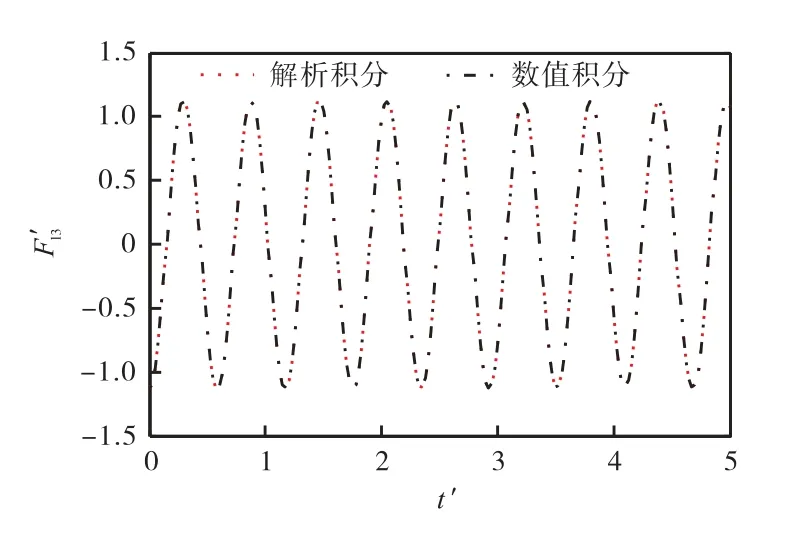
图4 无量纲垂荡F-K力时间历程(=0.5,d =0.5λ,Fr=0.2)Fig.4 Time history of non-dimensional heave F-K forces(=0.5,d =0.5λ,Fr=0.2)
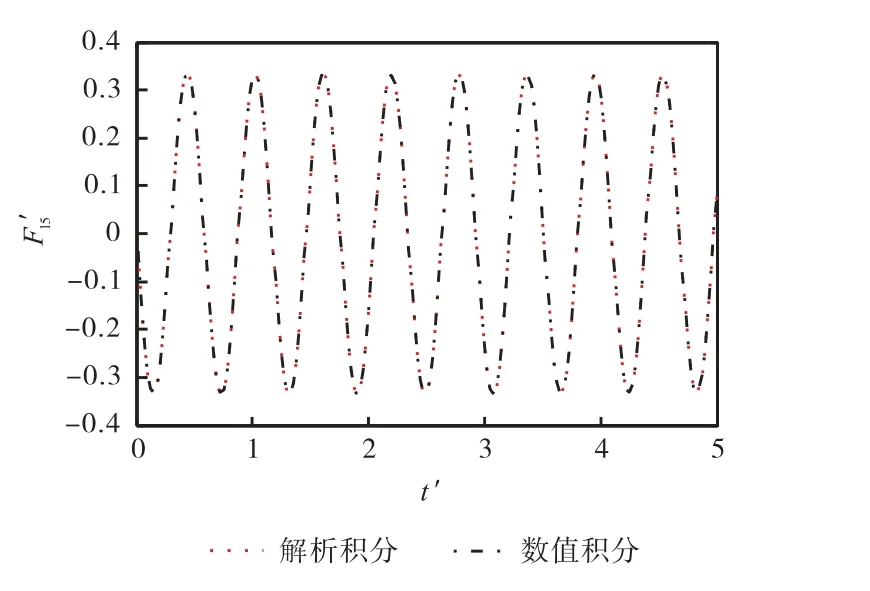
图5 无量纲纵摇F-K力时间历程(=0.5,d =0.5λ,Fr=0.2)Fig.5 Time history of non-dimensional pitch F-K forces(=0.5,d =0.5λ,Fr=0.2)
WigleyⅠ型船前后左右几何对称,如图 6 所示.本文选取第1象限中及3 个浪向角进行研究.在船舶航速下,对于不同入射波波长船长比λL 处,本文对影响F-K 力的流域水深d做进一步分析与探讨.其中,无量纲水深为
由图7~图12 可得,在不同入射波波长及浪向角下,当无量纲水深较小时,水深对F-K 力影响较为显著,不可忽略.当无量纲水深时,船体所受的 F-K 力逐渐趋于无穷水深所受到的F-K 力.
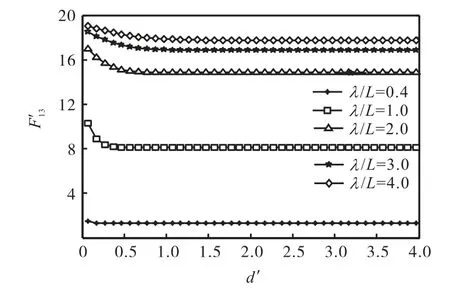
图9 无量纲垂荡F-K力幅值(β =)Fig.9 Amplitude of non-dimensional heave F-K forces(β =)

图11 无量纲垂荡F-K力幅值(β =)Fig.11 Amplitude of non-dimensional heave F-K forces(β =)
2.3 绕射问题分析与验证
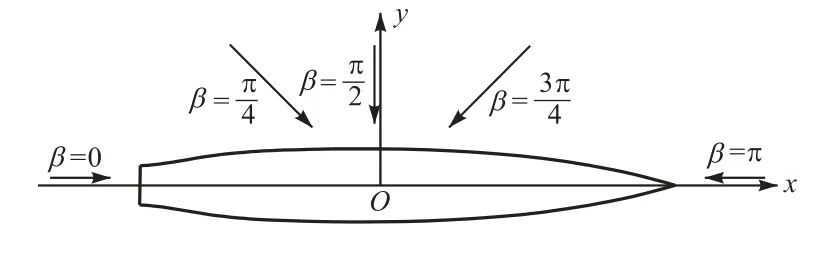
图6 浪向角示意Fig.6 Diagram of incident wave directions
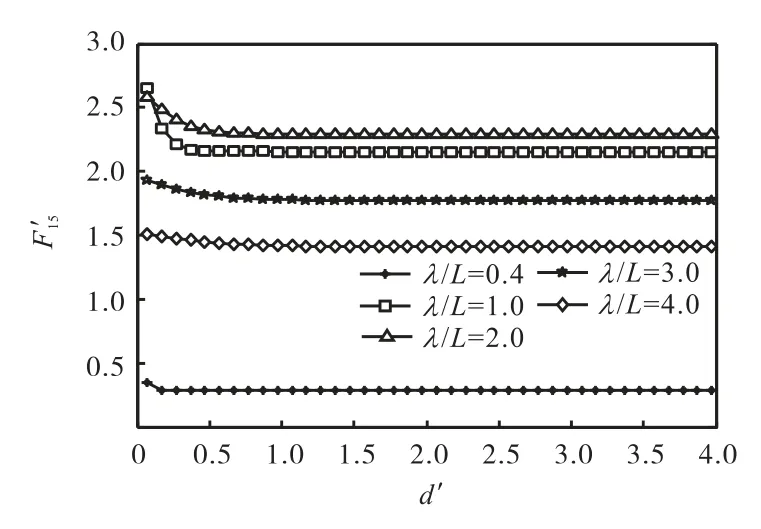
图8 无量纲纵摇F-K力幅值(β =π)Fig.8 Amplitude of non-dimensional pitch F-K forces(β =π)
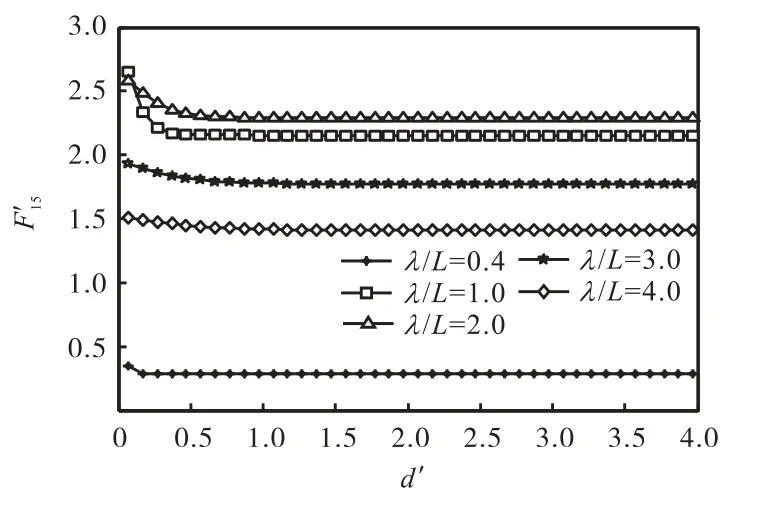
图10 无量纲纵摇F-K力幅值()Fig.10 Amplitude of non-dimensional pitch F-K forces()

图12 无量纲纵摇F-K力幅值(β =)Fig.12 Amplitude of non-dimensional pitch F-K forces(β =)
为与Journée[11]试验结果做比对,本文只对无限水深(即水深d 趋于无穷的情况)的WigleyⅠ型船进行垂荡、纵摇2 个自由度的波浪激励力数值模拟,船舶前进速度分别为Fr=0.2与Fr=0.3,基于本文计算模型所得结果表示为“本文方法”,基于Journée 试验所得结果为“试验结果”.
垂荡波浪激励力为Fw3,Fw3无量纲形式为纵摇波浪激励力为其无量纲形式为无量纲波数为
由图13~图16 可知,在大部分频率范围内,WigleyⅠ型船所受的垂荡波浪激励力与纵摇波浪激励力的频率响应函数均与试验值吻合良好,其中垂荡波浪激励力的预报效果优于纵摇波浪激励力.结果验证了本文提出算法的可靠性与有效性.
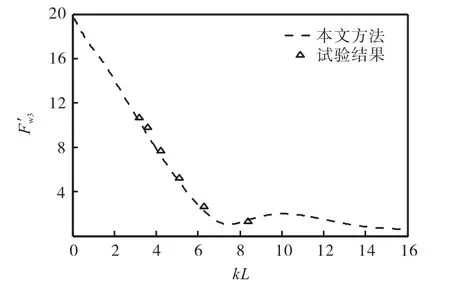
图13 无因次垂荡波浪激励力幅值(Fr=0.2)Fig.13 Non-dimensional heave amplitude of wave exciting force(Fr=0.2)
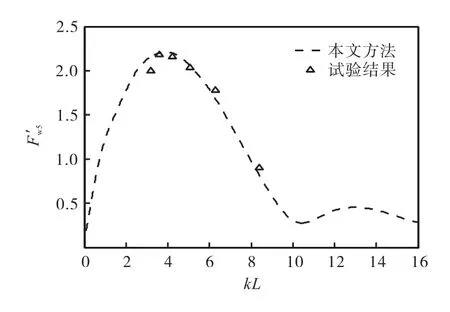
图14 无因次纵摇波浪激励力幅值(Fr=0.2)Fig.14 Non-dimensional pitch amplitude of wave exciting force(Fr=0.2)

图15 无因次垂荡波浪激励力幅值(Fr=0.3)Fig.15 Non-dimensional heave amplitude of wave exciting force(Fr=0.3)
此外,由于本文采用自由面时域格林函数计算波浪激励力,该方法基于Neumann-Kelvin 线性化自由面条件,其不能准确考虑航速效应的影响,在个别频率处计算结果与试验结果偏差较大.为了进一步提高波浪激励力的数值预报精度,可以采用简单Rankine 法,该方法不仅能准确地考虑航速效应,也能计入移动兴波对船体所受波浪激励力的影响,从而进一步提高船体受力及运动预报的数值精度.
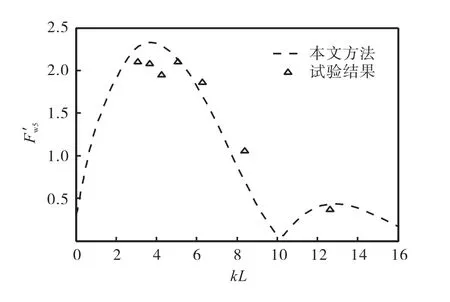
图16 无因次纵摇波浪激励力幅值(Fr=0.3)Fig.16 Non-dimensional pitch amplitude of wave exciting force(Fr=0.3)
3 结 论
(1)本文系统地推导了任意水深下船体所受F-K力的解析积分方法,可以避免由于数值积分所产生的误差,并大大减少船舶所需剖分的面元数量.对于形状规则的船体,比如驳船或者海洋钻井平台,只需要划分数量级面元即可满足计算要求.
(2)在一定入射波长及浪向角下,当流域水深较小时,水深因素对WigleyⅠ型船船体所受的F-K 力有较为显著的影响,不可忽视.随着水深的增加,特别当水深船长比大于0.5 时,有限水深中WigleyⅠ型船船体所受到的F-K 力越来越趋近于无限水深中船体所受到F-K 力.
(3)通过对无限水深中的以不同航速迎浪前进的WigleyⅠ型船进行计算仿真,其波浪激励力与试验值吻合良好,进一步证明了本文任意水深下船体所受F-K 力解析积分计算模型的精确性与可靠性.

