浅水波方程的一类改进的格子Boltzmann模型

陈文文 张文欢 汪一航 朱俏俐

浅水波方程的一类改进的格子Boltzmann模型

陈文文1, 张文欢1,2*, 汪一航1,2, 朱俏俐1

（1.宁波大学 数学与统计学院,浙江 宁波 315211; 2.宁波市非线性海洋与大气灾害系统协同创新中心,浙江 宁波 315211）

提出了一种改进的格子Boltzmann模型来模拟浅水流动. 新模型通过在演化方程中添加修正项,一个可调参数被引入到黏性系数与无量纲松弛时间的关系中,从而使得无量纲松弛时间的值在黏性系数固定时是可调的. 为了验证模型的精确性与稳定性,对圆柱绕流、流量驱动无外力浅水流进行了模拟. 数值结果表明,相较于以往模型,新提出模型在提高精度的同时,计算效率和稳定性也得到了改善.

格子Boltzmann方法; 浅水波方程; 无量纲松弛时间; 稳定性; 边界条件

近几十年来, 格子Boltzmann方法(LBM)由于计算简单、并行性好、易于处理复杂不规则的边界及能简单方便地考虑源项等优势, 已经发展成为求解浅水波方程(SWEs)的一种新方法. Salmon[1]最先成功将LBM应用于模拟风力驱动的海洋环流.冯士德等[2]将旋转流中存在的哥氏力效应引入到SWEs的格子Boltzmann(LB)模型的研究中,并在理想边界条件下模拟了北半球的大气环流. Zhou[3]则较系统地阐述了SWEs的LBM理论, 并对一些经典浅水波问题进行了验证. Thömmes等[4]采用LBM对直布罗陀海峡中的潮流进行了模拟. Klar等[5]开展了在复杂几何地形中通过LB模型对污染物扩散的潮流问题的实际研究. 接着, Liu等[6]成功将LBM应用于白洋淀的风力驱动水流模拟.以上研究表明, LBM具有良好模拟各种流体动力学情况下浅水流动的能力.

近年来, 为了进一步提高LBM模拟浅水流的精确性和稳定性, 不少学者也进行了改进. Zhou[7]采取了一种新颖方式将床层结合到格子Boltzmann方程(LBE)中, 消除了以往模型中底面坡度涉及到一阶导数的差分计算问题. Li等[8]提出了一种改进的浅水波LB模型, 其基本思想是将二次深度项从平衡态分布函数(EDF)中去除, 以避免EDF中二次深度项系数与LBE源项中的床斜率项系数之间的匹配要求. Peng等[9]分别使用具有单个松弛时间和多个松弛时间(MRT)碰撞项的LBM以求解SWEs, 并将力矩项的加权中心方案与河床坡度项中的水深结合, 以改进模型来模拟具有不连续床的浅水流. Peng等[10]指出具有单个松弛时间的LBE不太稳定, 并提出了SWEs的九速方格(D2Q9)上的具有2个松弛时间(TRT)的LBM以期能改进模型的稳定性.

与标准单松弛(LBGK)模型相比, TRT模型与MRT模型虽然在数值稳定性上有较大的优势[10-11], 但由于不止一个松弛时间, 在模拟计算中更加复杂. LBGK模型的稳定性很大程度上取决于无量纲松弛时间, 而无量纲松弛时间又与流体黏度或扩散系数有关. 如果无量纲松弛时间的值太大或太小(接近0.5), LBGK模型将很不稳定, 进而会因为数值不稳定而无法完成计算, 这极大地限制了模型在复杂流体流动研究中的应用. 为了克服LBGK模型在无量纲松弛时间方面存在的不足, 学者们进行了许多改进. Xiang等[12]在研究对流扩散方程的LBGK模型时, 将参数引入二阶矩条件中进行修正, 使得无量纲松弛时间的值在调整参数后不接近0.5. 尽管使用该方法可以提高LBGK模型稳定性, 但改进效果并不显著. Inamuro[13]提出了一种具有传热的不可压缩流体流动的晶格动力学方案(LKS). 在此方案中, 通过在平衡态分布函数中添加一个与应力张量(或热通量)有关的离散量, 无量纲松弛时间的值被固定为1.0. 然而, Yang等[14]指出LKS不满足质量守恒定律, 并针对求解不可压Navier-Stokes方程的LBGK模型提出了一种修正方案. 该方案通过在演化方程中加入修正项作为外力项或源项, 引入一个使松弛时间可调的参数, 无量纲松弛时间的选取更自由, 因此模型的稳定性得到提高.

本文基于Yang的改进模型思想, 提出针对二维浅水波方程的一种改进的LBGK模型来模拟浅水流动. 通过Chapman-Enskog多尺度分析, 所提出的改进模型可准确地恢复至二维浅水波方程. 新模型通过在源项中添加修正项, 在流体黏性系数与松弛时间的关系中引入一个可调参数, 此参数使得无量纲松弛时间的值可以保持在一个适当范围内, 从而提高了模型的稳定性.

1 浅水波方程(SWEs)

二维(2D)深度平均浅水波方程可用下式表示:

2 求解SWEs的改进LB模型的建立

针对求解2D浅水波方程的D2Q9-LBGK模型做出改进. 其中, 改进的演化方程如下:

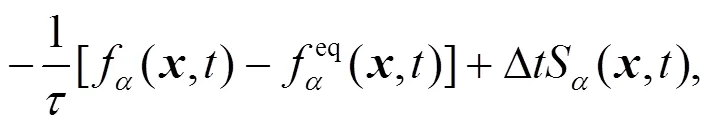
在D2Q9模型中, 离散速度定义如下:

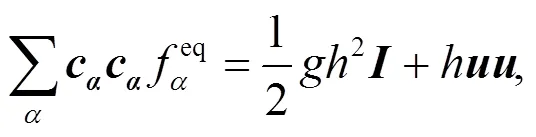
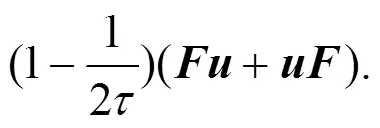
通过Chapman-Enskog多尺度分析[3,14], 该改进模型从演化方程(3)正确恢复至二维浅水波方程. 其中, 黏性系数定义为:

3 流入和流出的边界条件

3.1 考虑外力影响的进、出口边界条件

在入口边界由式(7)和(8), 可得以下3个方程:

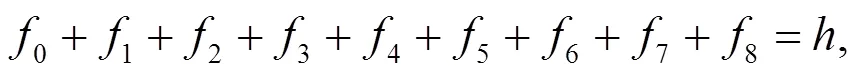
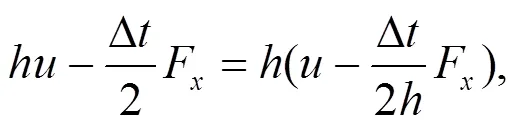
3.2 入口边界恒定流量

在模拟流动时, 通常设定入口边界条件为恒定流量, 入口处的速度和水深未知, 因此上述方案不再适用. Liu[16]提出了一种方法来处理这种入口边界, 即在水流方向上将恒定流量添加到动量方程中. 新方案以质量和动量守恒为基础, 同时包括以下2个步骤.

因此, 式(15)相应变为:

入口处的拐角点需要特殊处理. 以入口底部的拐角点为例, 分2种情形来讨论.

类似的过程可解出入口的顶部拐角点和出口的顶、底部拐角点的未知分布函数.

3.3 出口边界固定水深

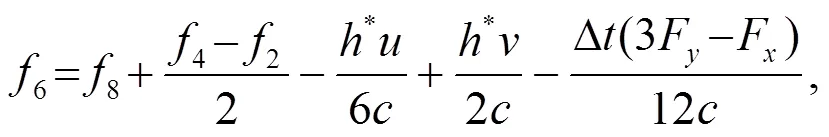
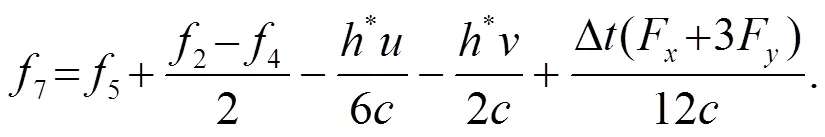
4 数值模拟

分别对圆柱绕流和流量驱动无外力浅水流进行数值模拟, 并将计算结果与其他数值方法结果对比, 以验证本文所提出模型的精确性和稳定性.

4.1 圆柱绕流

为验证模型的精确性, 分别使用Li等[8]和本文提出的模型对圆柱绕流进行模拟, 各种参数的设置与Zhou[3]的模拟保持一致. 模拟的流道长4m, 宽2m, 位于流道中心的是半径为0.11m的圆柱体, 左端为入口, 流入的流量及出口的水位皆为定值.

图2显示了本文模型在模拟达到稳定后圆柱体附近的流动特性, 这与zhou[3]绘制的图3有较好的一致性. 图4为Zhou和本文模型模拟得到的沿流道中心线上的水位结果与实验数据的对比. 其中, 本文所用实测数据是使用图像数据化软件(GetData Graph Digitizer)从参考文献[17]的图中获取. 由图5可知, 在圆柱后, 本文模型的模拟结果与Zhou模型的模拟结果很接近, 且都与实测结果吻合很好; 但在圆柱前, 本文模型的模拟结果与实测的结果更为接近. 为了定量比较2种模型模拟的精度的不同, 定义水位的相对误差为:

式中, 为实测值的数量; 和分别为水位的模拟值与实测值.经计算, 得出本文模型模拟水位的相对误差为1.16%, Zhou模型模拟水位的相对误差为1.65%, 说明本文模型在模拟圆柱绕流时的精度比Zhou模型更高. 值得注意的是, Li模型在进口流量m∙s-1时计算收敛, 但当进口流量增大为m∙s-1时计算发散, 这说明Li模型的稳定性没有本文提出的模型和Zhou模型的好.另外,由于实测数据是在进口流量m∙s-1的工况下采集, 而Li模型无法模拟得出此工况下的流速和水深数据, 因此文中没有展现有关Li模型的图表数据对比.

4.2 流量驱动的无外力浅水流

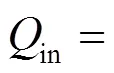
表1 入口流量为Qin=0.02 m3∙s-1, 3种模型皆达到R=1×10-8时所用的计算步数和时间

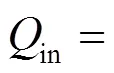
表2 入口流量为Qin=0.024 m3∙s-1,计算步数分别为50万、80万和100万步时的全局相对误差

表3 入口流量为Qin=0.0261 m3∙s-1,计算步数分别为50万、80万和100万步时的全局相对误差

5 结论

Yang等[14]针对求解不可压Navier-Stokes方程的LBGK模型提出了一种修正方案, 本文借鉴其改进模型的思路提出了一种求解二维浅水波方程的LBGK模型改进方案, 将一个修正项添加在标准LBGK模型的演化方程中, 作为源项的一部分, 使得在恢复宏观方程后流体黏性系数与无量纲松弛时间的关系中被引入了一个可调参数. 通过调节该参数的值, 无量纲松弛时间的值可保持在一个使计算稳定的范围内, 从而提高了模型的稳定性, 研究得出以下结论:

(1)在提出的改正模型正确恢复至二维浅水波方程的过程中, 应变率张量的计算采用了一个高效的局部计算格式. 梯度的计算仅通过局部信息便可得出, 避免了差分运算, 使得改进的LBGK模型保持了天然的并行性, 且易于处理具有复杂边界的物理问题.

[1] Salmon R. The lattice Boltzmann method as a basis for ocean circulation modeling[J]. Journal of Marine Research, 1999, 57(3):503-535.

[2] 冯士德, 赵颖, 茑原道久, 等. 旋转流场中的格子波耳兹曼模型[J]. 地球物理学报, 2002, 45(2):170-175.

[3] Zhou J G. Lattice Boltzmann Methods for Shallow Water Flows[M]. Berlin: Springer, 2004:7-18.

[4] Thömmes G, Seaïd M, Banda M K. Lattice Boltzmann methods for shallow water flow applications[J]. International Journal for Numerical Methods in Fluids, 2007, 55(7):673-692.

[5] Klar A, Seaïd M, Thömmes G. Lattice Boltzmann simulation of depth-averaged models in flow hydraulics [J]. International Journal of Computational Fluid Dynamics, 2008, 22(7):507-522.

[6] Liu H F, Li M, Zhao Y W. Application of the lattice Boltzmann method in shallow water lake[J]. Advanced Materials Research, 2011, 356:2333-2337.

[7] Zhou J G. Enhancement of the LABSWE for shallow water flows[J]. Journal of Computational Physics, 2011, 230(2):394-401.

[8] Li S T, Huang P, Li J M. A modified lattice Boltzmann model for shallow water flows over complex topography [J]. International Journal for Numerical Methods in Fluids, 2015, 77(8):441-458.

[9] Peng Y, Zhou J G, Zhang J M, et al. Lattice Boltzmann modeling of shallow water flows over discontinuous beds[J]. International Journal for Numerical Methods in Fluids, 2014, 75(8):608-619.

[10] Peng Y, Zhang J M, Zhou J G. Lattice Boltzmann model using two relaxation times for shallow-water equations[J]. Journal of Hydraulic Engineering, 2016, 142(2):5017- 5025.

[11] Lallemand P, Luo L S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance and stability[J]. Physical Review E, 2000, 61(6):6546-6562.

[12] Xiang X, Wang Z, Shi B. Modified lattice Boltzmann scheme for nonlinear convection diffusion equations[J]. Communications in Nonlinear Science & Numerical Simulation, 2012, 17(6):2415-2425.

[13] Inamuro T. A lattice kinetic scheme for incompressible viscous flows with heat transfer[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2002, 360(1792):477- 484.

[14] Yang X G, Shi B C, Chai Z H. Generalized modification in the lattice Bhatnagar-Gross-Krook model for incompressible Navier-Stokes equations and convection- diffusion equations[J]. Physical Review E, 2014, 90(1): 13309-13326.

[15] Zou Q, He X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model[J]. Physics of Fluids, 1997, 9(6):1591-1598.

[16] Liu H F. Lattice Boltzmann simulations for complex shallow water flows[J]. Clinical Infectious Diseases, 2009, 28(3):560-571.

[17] Yulistiyanto B, Zech Y, Graf W H. Flow around a cylinder: Shallow-water modeling with diffusion- dispersion[J]. Journal of Hydraulic Engineering, 1998, 124(4):419-429.

[18] Mei Q Y, Zhang W H, Wang Y H, et al. Lattice Boltzmann study on seawall-break flows under the influence of breach and buildings[J]. Communications in Theoretical Physics, 2017, 68(4):525-535.

A modified lattice Boltzmann model for shallow water flows

CHEN Wenwen1, ZHANG Wenhuan1,2*, WANG Yihang1,2, ZHU Qiaoli1

( 1.School of Mathematics and Statistics, Ningbo University, Ningbo 315211, China; 2.Ningbo Collaborative Innovation Center of Nonlinear Hazard System of Ocean and Atmosphere, Ningbo 315211, China )

A modified lattice Boltzmann model is proposed to simulate shallow water flows. The new model introduces an adjustable parameter in the relationship between the viscosity coefficient and the dimensionless relaxation time by adding a correction term to the evolution equation, so that the dimensionless relaxation time is adjustable when the viscosity coefficient is fixed. In order to verify the accuracy and stability of the model, the flow around the cylinder and the discharge-driven shallow water flow without external force is simulated.The numerical results show that compared with the previous approaches, the proposed model is improved not only in accuracy, but also in computational efficiency and stability.

lattice Boltzmann model; shallow water equations; dimensionless relaxation time; stability; boundary conditions

TV131.2

A

1001-5132（2020）01-0072-08

2019−06−21.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

宁波市自然科学基金（2016A610075）.

陈文文（1994－）, 女, 安徽六安人, 在读硕士研究生, 主要研究方向: 格子Boltzmann建模. E-mail:2514805223@qq.com

张文欢（1986－）, 男, 湖北黄冈人, 博士/讲师, 主要研究方向: 格子Boltzmann建模. E-mail: zhangwenhuan@nbu.edu.cn

（责任编辑 章践立）