Well-posedness for A Plate Equation with Nonlocal Source term
LIU Gong-wei, ZHAO Rui-min, ZHANG Hong-wei
(College of Science, Henan University of Technology, Zhengzhou 450001, China)
Abstract: In this paper, we investigate the initial boundary value problem for a plate equation with nonlocal source term. The local,global existence and exponential decay result are established under certain conditions. Moreover, we also prove the blow-up in finite time and the lifespan of solution under certain conditions.
Key words: Plate equation; Nonlocal source term; Decay estimate; Blow-up
§1. Introduction
In this paper, we shall deal with the following plate equation with nonlocal source term

where Ω is a bounded domain in Rnwith sufficiently smooth boundary ∂Ω, ν is the unit outer normal to ∂Ω, u0(x) and u1(x) are given initial data, N is a nonpositive function on R+which is defined in Section 2. The exponent p satisfies
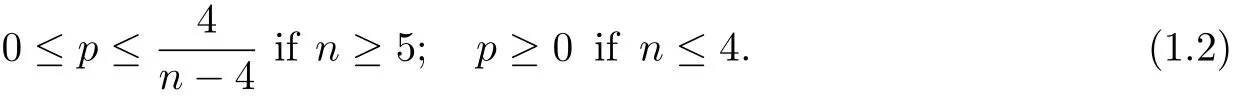
In fact, the classical beam equation is a description of the change of the state of the elastic beam by the fourth-order partial differential equation
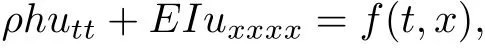
where u is the vertical displacement of the beam in the downward direction,f(t,x)is the forcing term, ρ is the density of the beam, E is the elastic coefficient of the beam and I is inertia of section of neutral beam. For plate equation with polynomial source term, Messaoudi[7]studied the following problem
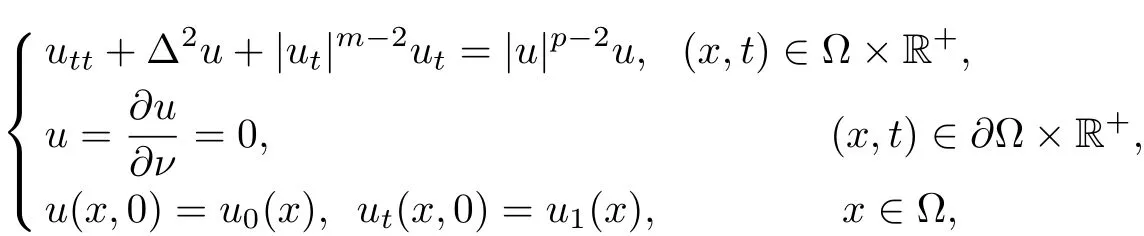
he established the existence result and showed that the solution continues to exist globally if m ≥p and blows up in finite time if m
The problem of plate equations with nonlocal source terms has caught the attention by many mathematicians in recent decades. In [5], Khanmamedov and Simsek considered the following plate equation
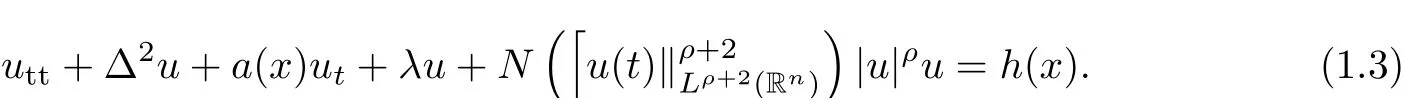
Under proper conditions on the damping coefficient, they established that the dynamical system associated with (1.3) possesses a global attractor. In particular, the nonlocal sourcewith ρ = 0 arise in Kerr-like medium models [6, 13]. Recently, Narciso [10]investigated the following plate equation with damping and source terms given by the product of two nonlinear components

where I1(u(t)) = M(∇u(t)) and I2(u(t)) =. The existence of solution and a compact global attractor are obtained [10].
Motivated by the above mentioned researches, in this paper, we intend to study the initial boundary value problem (1.1). The nonlocal source term in our paper is in the right hand side of the equation which is different from (1.3) and (1.4). For the related nonlocal source term,we also mention the paper [4], where the following equation
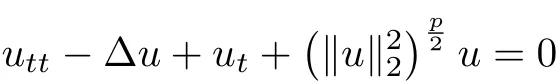
with Neumann boundary condition was considered. We notice here that the nonlocal source termon the right hand side may cause finite-time blow-up of solution to the problem (1.1) which is similar as the classical polynomial source term |u|p−2u, but we need more careful computation.
§2. Preliminaries and Main Results
In this paper, We denote the standard Lebesgue space Lp(Ω) and Sobolev spacewith usual scalar products and norms. We introduce the Sobolevs embedding inequality :. We also use C and Cito denote positive constant that may have different values in different lines.
Now, we need the following assumptions about the function N,
(H) N is a C1function on [0,+∞) with N(s)≥0 and satisfies
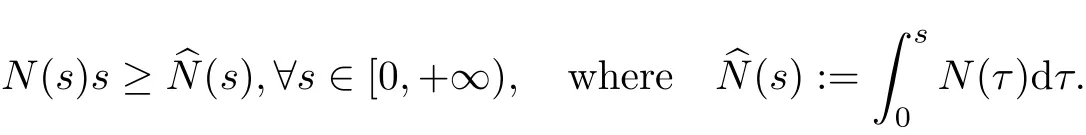
For simplicity, we assume 0 ≤N(s)≤µskwith k ≥0.
Theorem 2.1If u0∈H20(Ω),u1∈L2(Ω), (1.2) and the assumption (H) hold, then there exists T > 0 such that the problem (1.1) has a unique local solution u(t) in the classwith ut∈L2([0,T],L2(Ω)).
Next, we will discuss the global existence, energy decay and blow-up of the solution under N(s)=µsk. Hence, we can obtain. We define the following functions:
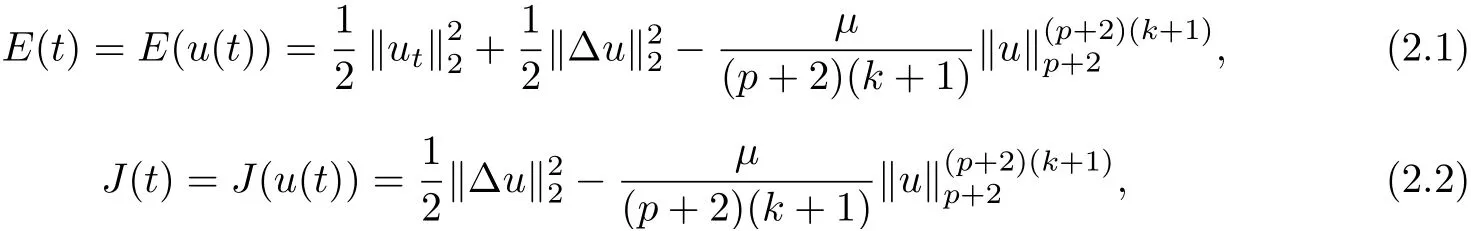
and

The potential well depth of the functional J(u(t)) is defined by
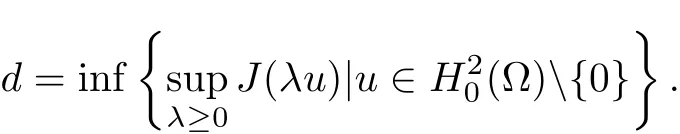
Theorem 2.2Let u(t)be the unique local solution to problem(1.1)obtained in Theorem 2.1. Assume I(u0)>0 and

hold,then the problem(1.1)admits a global solution. Moreover,there exists positive constants M and κ such that

Theorem 2.3Let u(t) be the unique local weak solution to problem (1.1) obtained in Theorem 2.1, if one of the following
(i)0 ≤E(0)
(ii)E(0)<0,
where E1and λ1are defined by (3.17) and (3.16), respectively, then u(t) blows up at a finite time T. Moreover, the lifespan can be established by 0 In this section, we shall give the proof of main results. For every T >0, Let us consider the space endowed with thenorm Lemma 3.1Suppose that (1.2) holds, u0∈H20(Ω) u1∈L2(Ω) and u ∈H, then there exists v ∈H∩C2(|0,T|,H−2(Ω))with vt∈L2(|0,T|,L2(Ω))which solves the following equation ProofWe employ the standard Garlerkin approximation scheme. Letbe the orthogonal complete system of eigenfunctions of ∆2inwith= 1 for all i, and Wh= Span{w1,...,wh}. We denote by {λi} the related eigenvalues to their multiplicity. We should seek h functions γ1h,...,γhh∈C2[0,T]for each h>0 such that solves the following problem For i = 1,...,h, taking η = wiin (3.1) yields the following Cauchy problem for the ordinary differential equation with unknown γih where Then the above problem admits a unique local solution γih∈C2[0,T]for all i, which in turn implies a unique vhdefined by (3.2) satisfying (3.3). By young’s inequality, we can deduce that Combining the above two inequalities, we can have where C >0 is independent of h. Therefore, as usual, up to a subsequence, we may pass to the limit in (3.3) and obtain a weak solution v of (3.1) with the required regularity. Then we prove the uniqueness of solution. If v1and v2were two solutions of (3.1) which shall the same initial data, putting w =v1−v2, we could obtain which implies that w =0, i.e. v1=v2. The proof of the lemma is now complete. Proof of Theorem 2.1For u0∈H02(Ω),u1∈L2(Ω),we denote R2:=2and BR:={u ∈H|u(0,x)=u0(x),ut(0,x)=u1(x),≤R}for every T >0. It follows from Lemma 3.1, for any u ∈BR, we could define a map Φ : H →H defined by v = Φ(u), where v is the unique solution to (3.1). Now let us prove that Φ is contract mapping. By the similar argument, we obtain Taking T is sufficiently small, we havewhich yields that Φ(BR)⊆BR. Taking v1= Φ(w1),v2= Φ(w2) with w1,w2∈BR, and v = v1−v2, we deduce that v satisfies Taking η =vt=v1t−v2t, and integrating both sides of above equation over (0,t), we obtain We shall compute the last term of the right hand side of (3.5). First,we estimate I1. Using N ∈C1[0,+∞),H¨older’s inequality withand Sobolev’s embedding, we have Now, let us estimate the term I2. After a simple computation, we have Hence, we can estimate I2as Inserting (3.6) and (3.5) into (3.5), we have for some δ < 1 when T is sufficiently small. By the Contract Map Principle [2-3], there exists a unique weak solution to (1.1) defined on [0,T]. This completes the proof of Theorem 2.1. Now we are in the position to prove the global existence and the energy decay rate. Lemma 3.2Let u(t) be the solution obtained in Theorem 2.1, Moreover, if I(u0) > 0 and (2.4) hold, then, I(u(t))>0 for t ∈[0,T]. ProofIt follows from the continuity of I(u(t)) that I(u(t)) ≥0 for some interval near t=0, let tmaxbe the maximal time (possibly tmax=T). It follows from (2.2) and (2.3) that Hence, from (2.2) and (2.3), we have and Hence, we have I(u(t))>0 on [0,tmax). This implies that we can take tmax=T. Proof of Theorem 2.2It follows (2.1), (3.8) and Lemma 3.2 that Multiplying both sides of the equation (1.1) by utand integrating over Ω×[t,t+1], we have Thus,it follows(3.11)that there exist t1∈t,t+and t2∈t+,t+1satisfying4D(t)2, i=1,2. Next, multiplying (1.1) by u(t) and integrating in over Ω×[t1,t2], we get It follows from (3.9) that and Hence, we have Thanks to (2.3) and (3.10), we have where η ∈(0,1) by (2.4). Hence, using (2.1) and (2.3) and (3.13), we obtain Hence, combining (3.12) and (3.13), we have where C2=and C3=4+2C1+which implies Hence, we apply Nakao’s inequality [9]to (3.14) to obtain the decay estimate (2.5). The proof of Theorem 2.2 is complete. In the following part, we will give the proof of the Theorem 2.3. By the definition of E(t),we get It is easy to see that G(λ) has the maximum at and the maximum value is Lemma 3.3Suppose E(0) (i)if<λ1, then<λ1for t ≥0. (ii)if>λ1, then there exists λ2>λ1such that≥λ2for t ≥0. ProofThe method of the proof is similar to [15]. See also the We omit it here. Proof of Theorem 2.3(i) When 0 ≤E(0) where E2=Then, from (3.18), we have Let By differentiating both sides of (3.19) and using (1.1), we get Hence, by (2.1), we have where λ2is given by Lemma 3.3, C4=C5=−(p+2)(k+1)E2. It follows from Lemma 3.3 (ii) that C4>0. By (3.17), we have Combining (3.20) with (3.21), we have that Then, using H¨older’s inequality, we have From (3.15) and (3.18), we obtain Moreover By Young’s inequality, we see that where α1=>0, ε>0. Then, by (3.23), letting 0<α<α1, we obtain Now, we define where δ1>0 . By differentiating (3.25), from (3.22) and (3.24) we get Hence, from (3.18), we obtain Now, we choose ε>0 sufficiently small such thata nd 0<δ1<. Thus, we can obtain where C7= min,a1−a3,C4−a3,(p+2)(k+1)−Since L(t) is a nonincreasing function as t ≥0. We choose δ1sufficiently small in (3.25) such that L(0) > 0. Now,letting η =since α<α1<1, we have 1<θ Applying H¨older’s inequality and Young’s inequality, we have So, we have Since θβ1=<(p+2)(k+1), combining (3.28)-(3.30), we see that It follows from (3.27) and (3.31), we see that where C9=. Integrating (3.32) over (0,t), we have Since,L(0)>0,(3.33)yields that L(t)blows up in some finite time T,where T ≤T∗= (ii) For E(0) < 0, we take H(t) = −E(t) instead of (3.18). Then, by the similar argument as in the part (i), we have the result. The proof of Theorem 2.3 is complete. AcknowledgmentsThe authors would like to thank the referees for the careful reading of this paper and for the valuable suggestions to improve the presentation and the style of the paper.§3. Proof of The Main Results

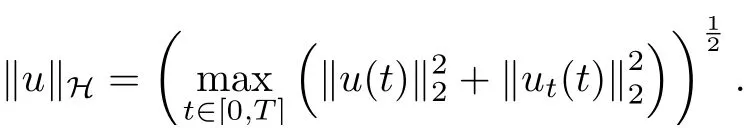



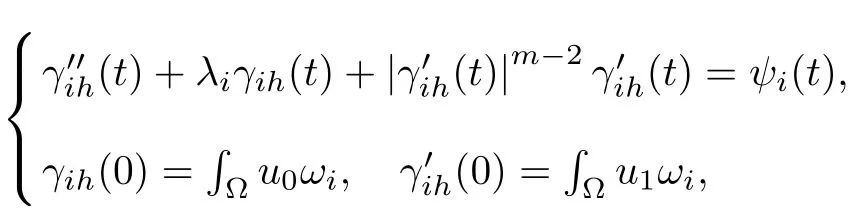
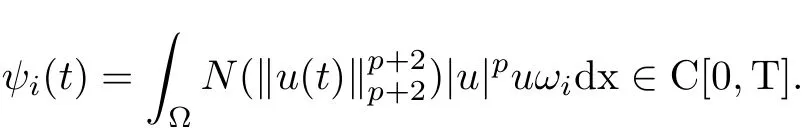
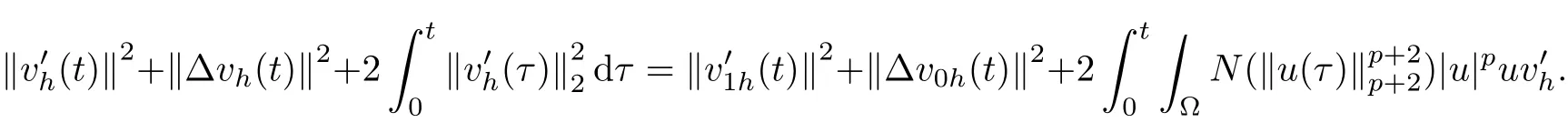
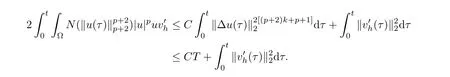
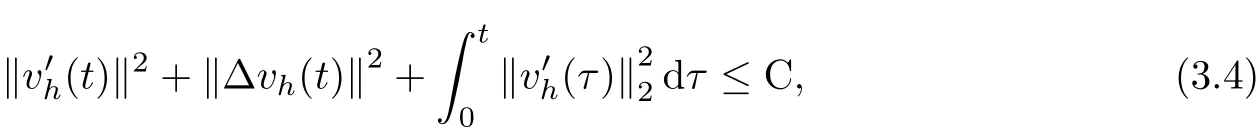

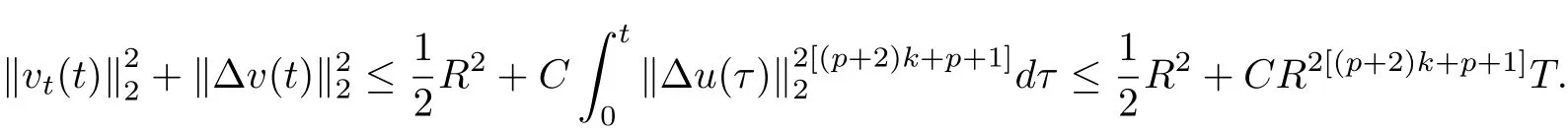
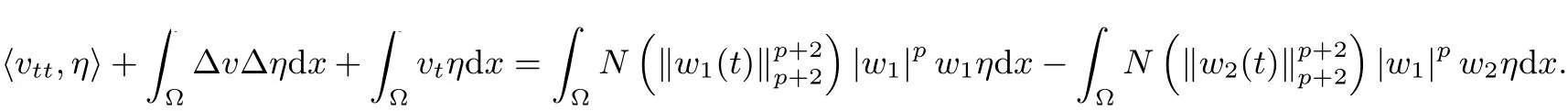
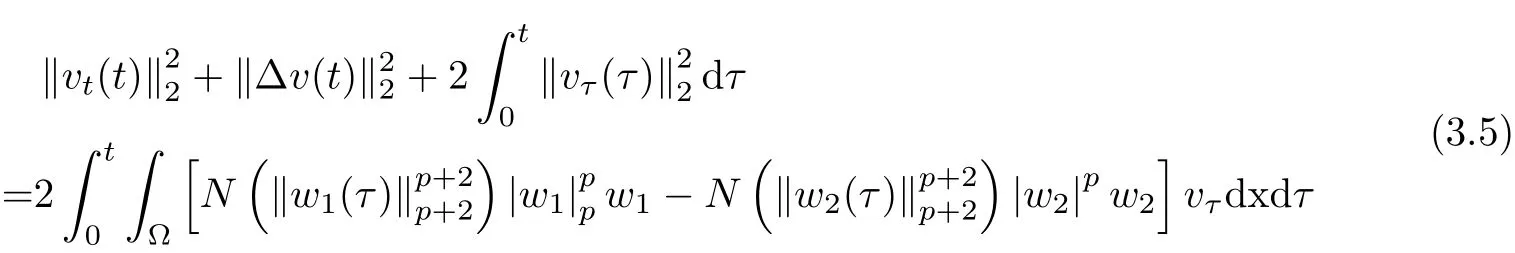
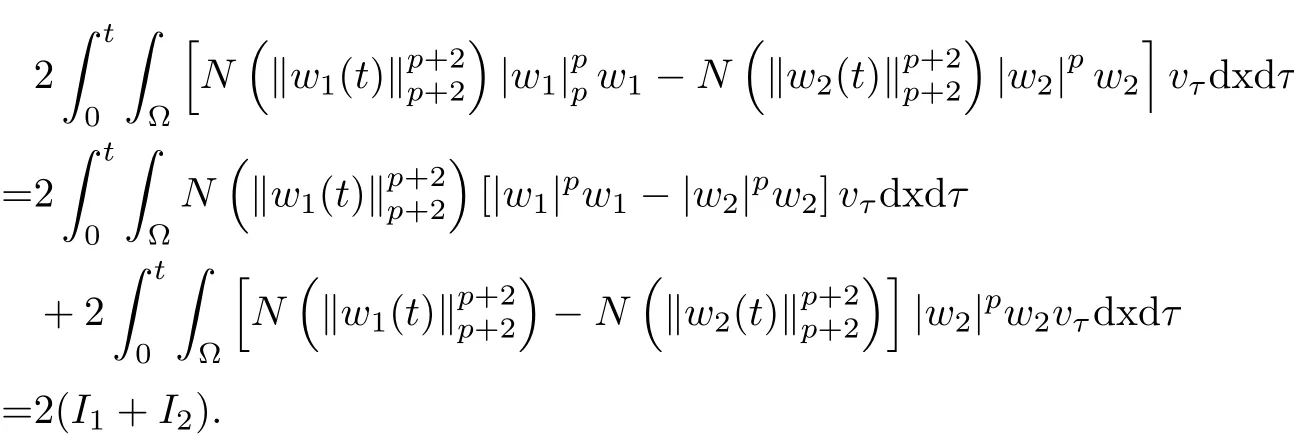
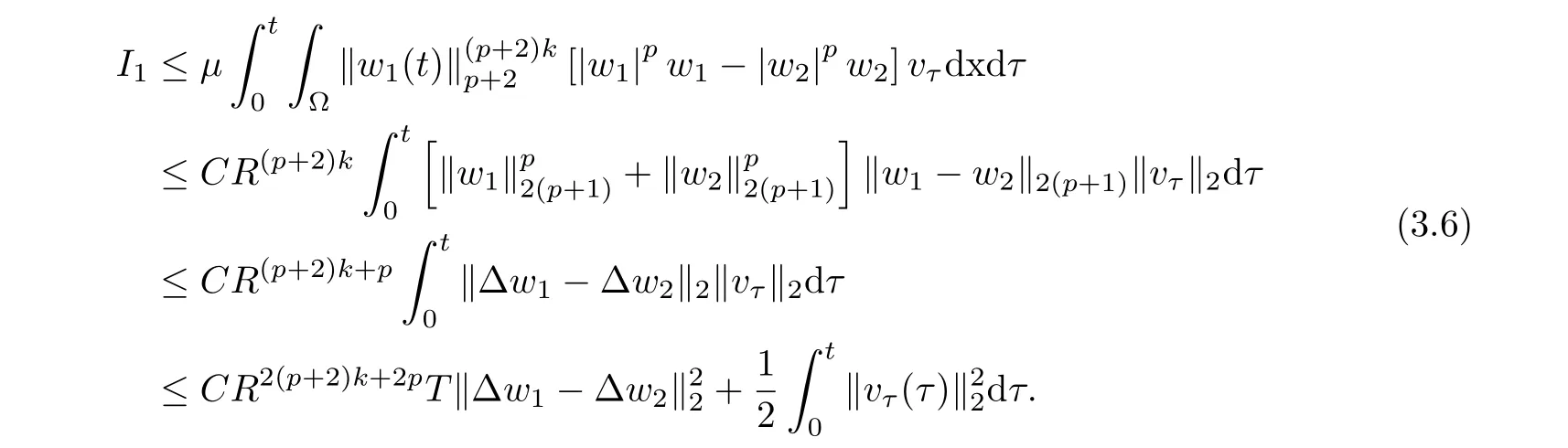
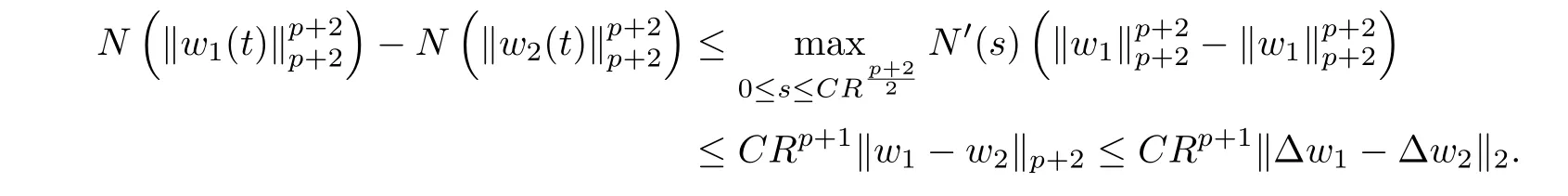

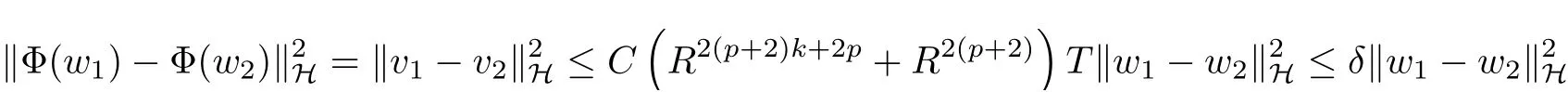
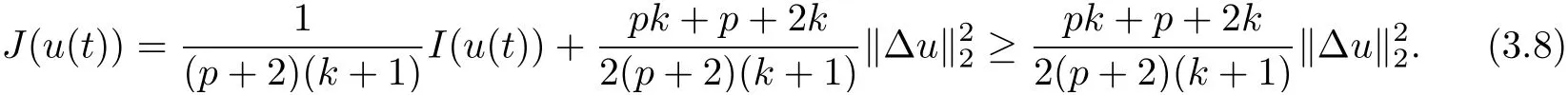
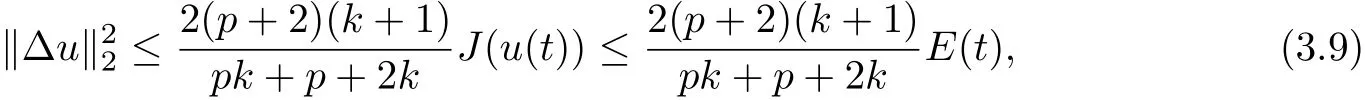
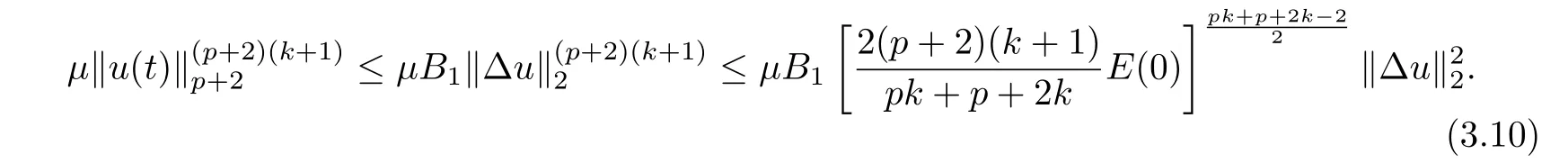
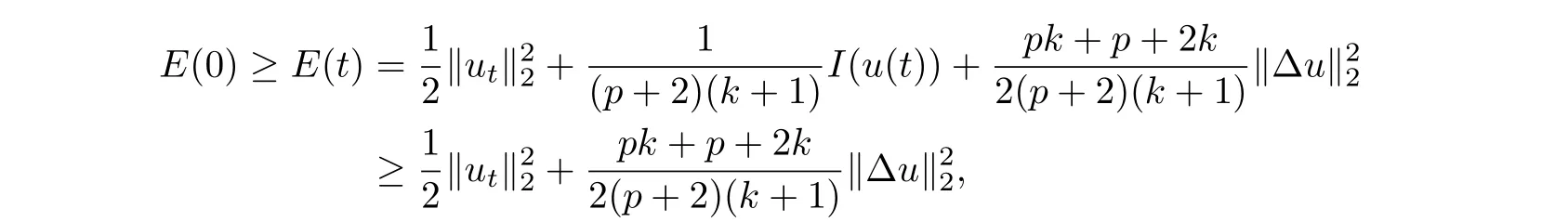
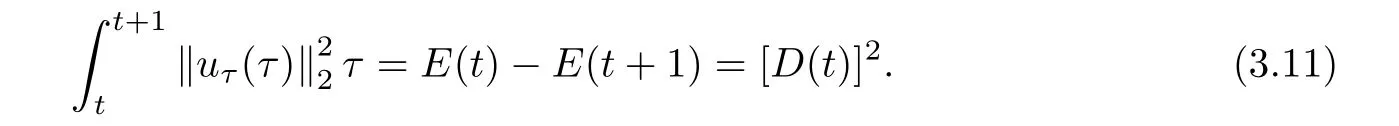
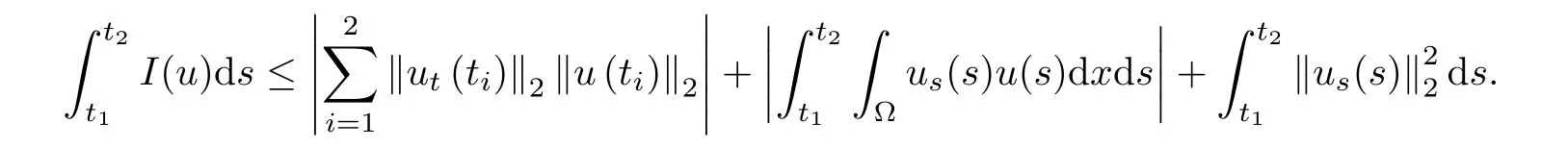
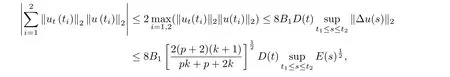
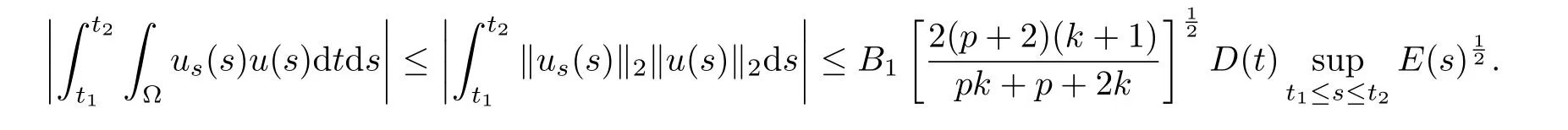


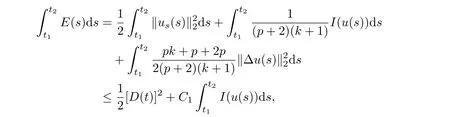
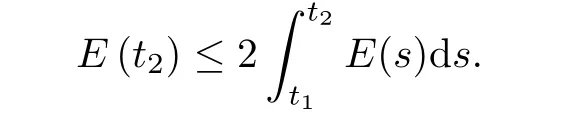
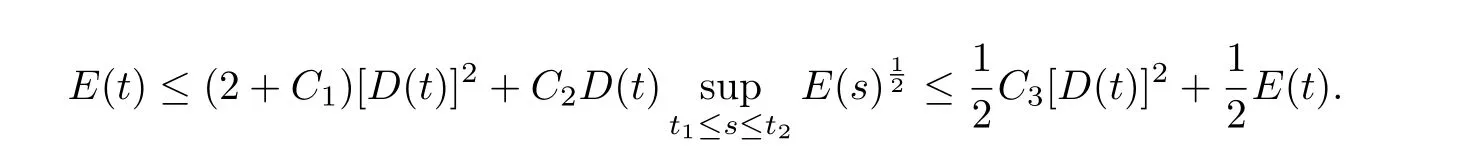

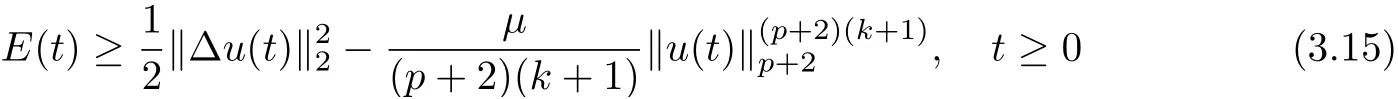
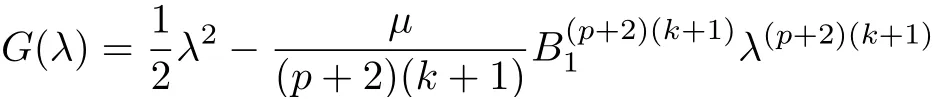
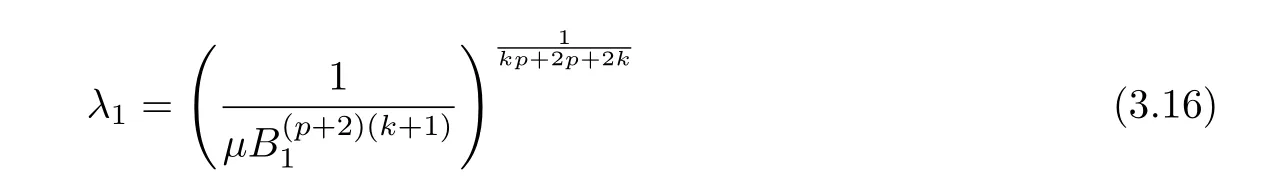
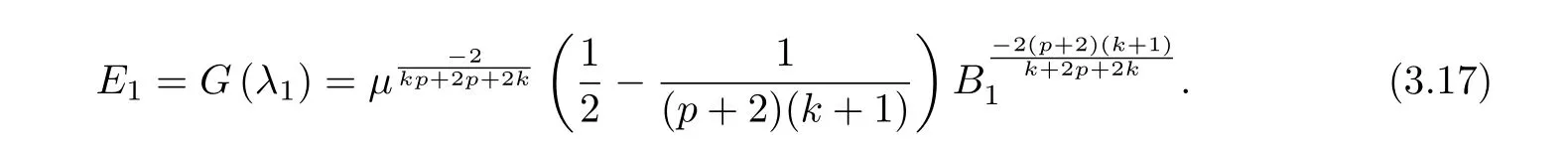

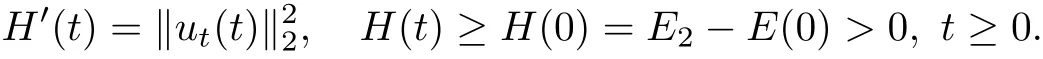
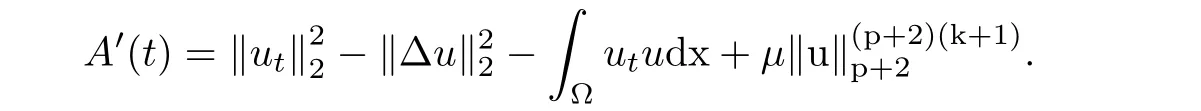

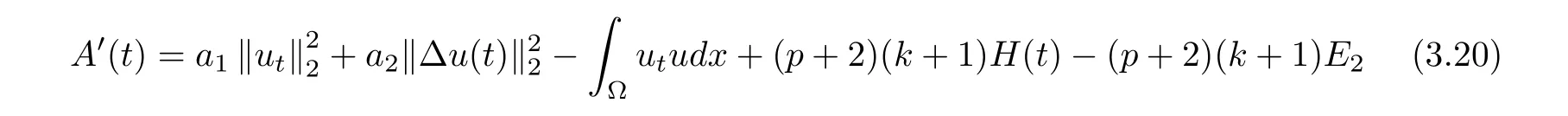
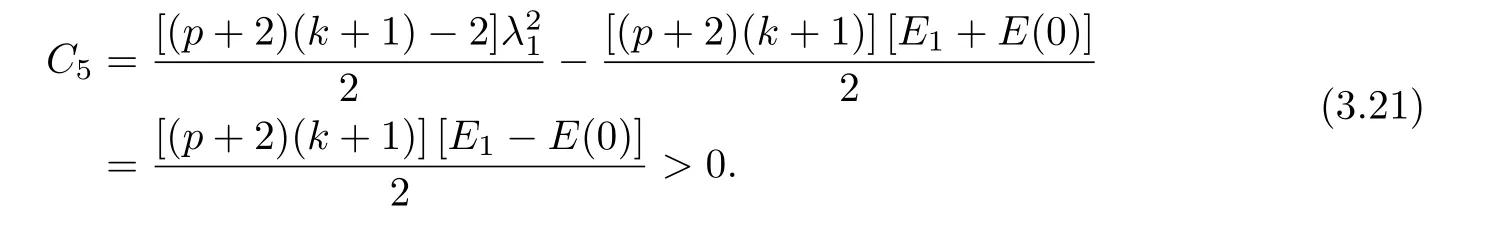
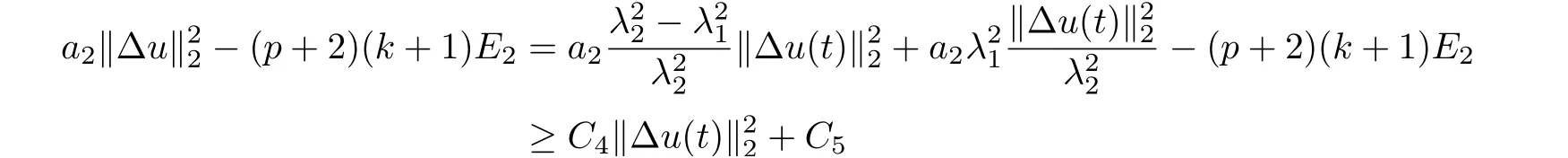

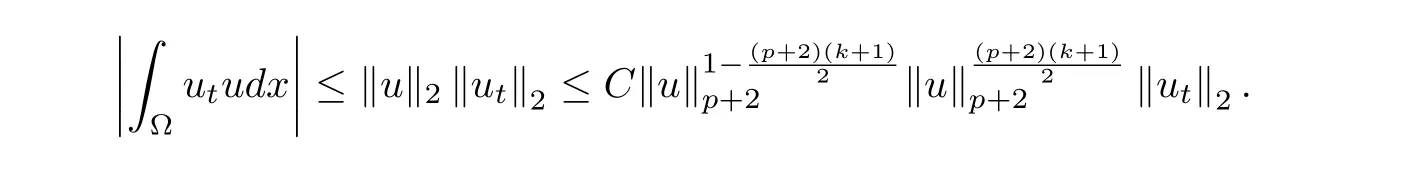
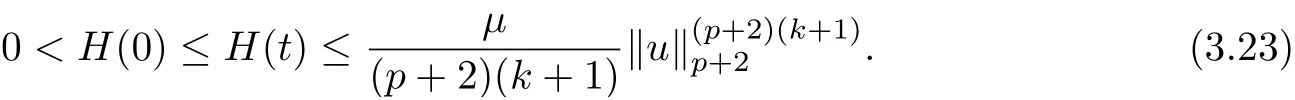

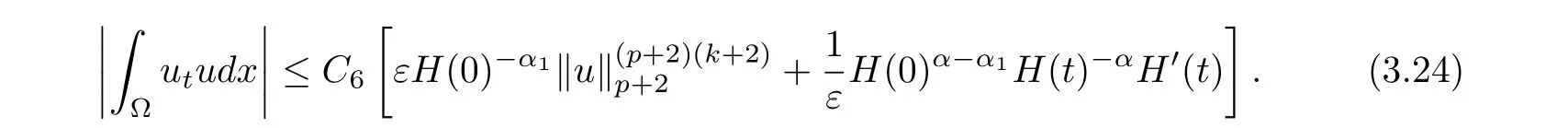
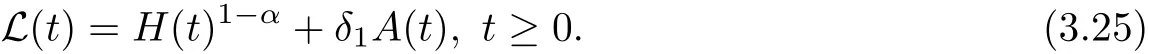

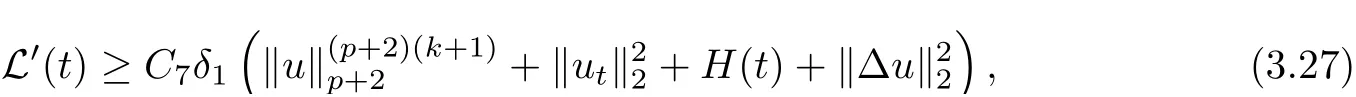

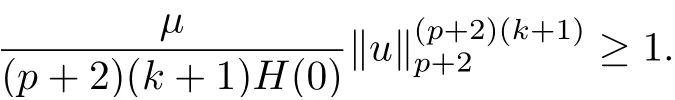
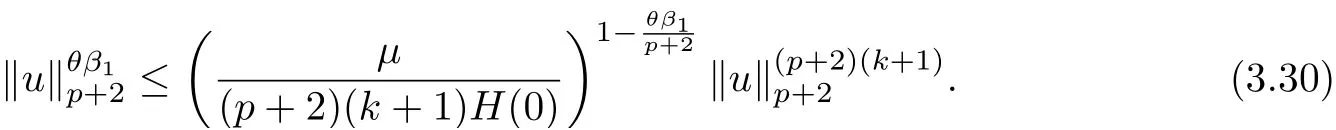
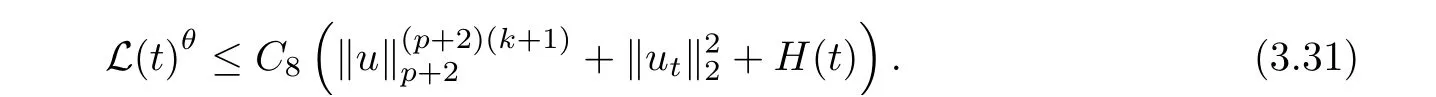

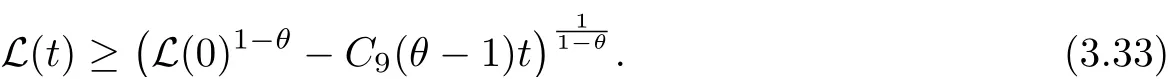
 Chinese Quarterly Journal of Mathematics2019年4期
Chinese Quarterly Journal of Mathematics2019年4期
