朱砂根盆花果实数量指标一元线性回归方程的建立

张森行

摘要：为探索朱砂根盆花果实结果枝数、结果量、果实直径之间的关系，通过对武平县钦福花场绿叶型的朱砂根盆花进行抽样调查，调查内容包括结果枝数、结果量、果实直径3项指标，并在R语言程序中，利用函数hiSt（）、plot（）、cor（）、cor.test（）、Im（）、Sum-mary（）、predict（）及相关命令对调查结果进行直方图分析、散点图分析、相关分析及t检验、回归分析及t检验、一元线性方程预测。结果：3项指标呈近正态分布，并存在线性相关关系;结果枝数、结果量的相关系数为0.6106085，结果枝数与果实直径的相关系数-0.2811521，结果量与果实直径的相关系數-0.4104362，均通过t检验;结果枝数与结果量的一元线性回归方程为v=-283.04+62.83x，结果枝数与果实直径一元线性回归方程为：y=9.42124-0.06184x，结果量与果实直径的一元线性回归方程为y=9.023579-0.0008772x，均过t检验;一元线性回归方程预测结果与实际调查值相符或相近。

关键词：朱砂根盆花;果实数量指标;相关分析;回归分析;一元线性回归方程;预测

朱砂根）盆花，商品名为富贵籽，是福建省成功驯化开发的特色野生花卉品种。作为观果花卉，它的主要特点是以树冠中部的果实为主要观赏点，所以它的结果枝数、果实量、果实直径为最主要的数量规格指标。为探索结果枝数、果实量、果实直径之间的相关关系，建立果枝数、果实量、果实直径之间一元线性回归方程;在栽培种植措施不变的前提下，测算单株果实量、果实直径达到特定值所需的结果枝数和结果量。2019年1～2月，在武平县东留镇的钦福花场，对绿叶型朱砂根盆花开展了调查分析。

1产地概况和花场生产条件与措施

1.1产地概况

武平县位于武夷山脉的最南端，东经115°51～116°23，北纬24°47～25°29，属亚热带海洋性季风气候，温暖湿润，雨量充沛，降雨相对集中，干湿季节明显，四季分明，夏长冬短。2月中旬，全县平均气温开始达到10℃以上，进入春季，历时80d左右;5月上旬，平均气温开始达到22℃以上，进入夏季，历时160d左右;10月上旬，开始进入秋季，历时80d左右;12月下旬，平均气温开始低于10℃，进入冬季，历时40d左右。

1.2苗圃生产条件与措施

钦福花场的设施条件为肩高1.8m、拱高3.Om的连拱钢架薄膜塑料大棚，外加一层透光率约70%黑色针织遮阳网;18cm×20cm塑料薄膜容器袋袋栽，栽培基质为（30%）椰糠+（70%）塘泥土。采用武平县富贵籽花卉协会推广应用的朱砂根盆花生产技术措施。

2调查方法与内容

2.1抽样

按《花卉检验技术规范第3部分：盆花检验》规定，以盆为单位抽取，用“x”法抽取，每条线上的抽取点视批量而定，抽取点数最少不少于3点，每点取1盆，共50盆。

2.2调查内容

结果枝数、果实量、果实直径3项。

2.3调查方法

结果枝数以目测计数，生长着果实的枝条全部计人;果实直径用游标卡尺测量，选取有代表性的3个果实测量，以平均值为果实直径;果实数量：先选取有代表性的3个果序计算果实数，计算果序上的平均果实数，然后以果序上果实平均数乘以结果枝数算结果量。

3调查结果与分析

3.1结果

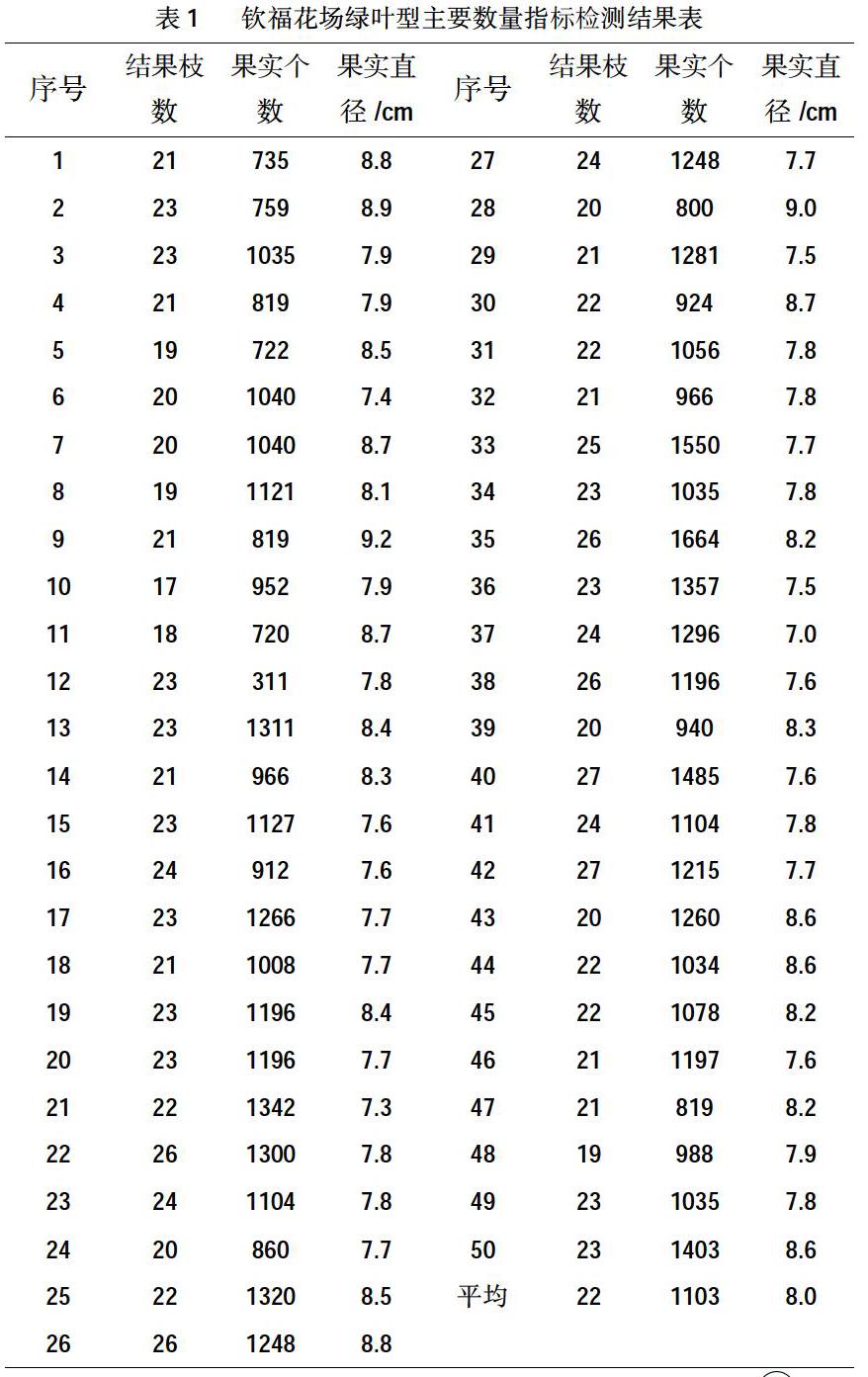
结果枝数、结果量、果实直径检测结果见表1，经计算平均结果枝数22枝、平均结果量1 103个、平均果实直径8.0cm。

3.2分析

调查数据采用R语言程序统计分析。3.2.1直方图分析。分别将表1中的结果枝数、结果量、果实直径按1枝、100个、0.5cm为1级分级，并输入R语言程序中，植入函数hist（），分别输出它们的直方图（图1、图2、图3）。从直方图的形状可以判断，结果枝数、结果量、果实直径的数值是呈近正态分布。

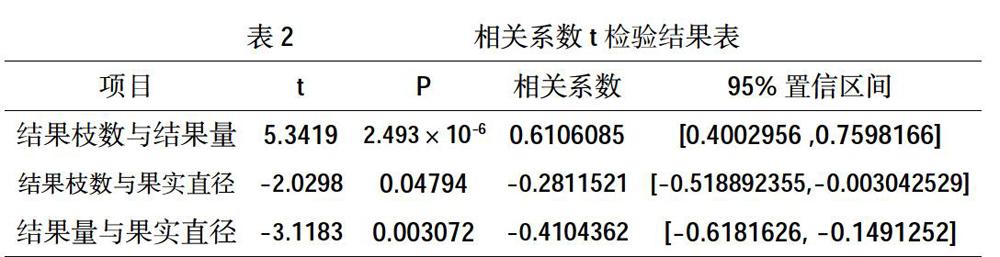
3.2.2散点图分析。在R语言程序中，植入函数plotO和命令ablineO，分别输出它们的散点图（图4、图5、图6）。从散点图的形状可判断，结果枝数与结果量、结果枝数与果实直径、结果量与果实直径存在线性相关关系。3.2.3相关分析。在R语言程序中，植入函数cor（），分别求得结果枝数与结果量的相关系数r=0.61 06085，结果枝数与果实直径的相关系数r=-0.281 1 521，结果量与果实直径的相关系数r=-0.4104362。3.2.4相关系数t检验。在R语言程序中，植入函数cor.testO，分别求得检验的t统计量、对应的检验P值、相关系数、95%置信区间（表2）。

结果枝数与结果量的t统计量的值为5.3419，明显大于对应的检验P值2.493×10-6，它们存在相关系数0.6106085的正相关，相关系数95%的置信区间为[0.4002956，0.7598166]。结果枝数与果实直径的的t统计量的值为-2.0298，绝对值明显大于对应的检验P值4.794×10^-2，它们存在相关系数一0.2811521的负相关，相关系数95%的置信区间为[-0.518892355，-0.003042529]。结果量与果实直径的t统计量的值为-3.1183，绝对值明显大于对应的检验P值3.072×10^-3，它们存在相关系数-0.4104362的负相关，相关系数95%的置信区间为[-0.6181626，-0.1491252]。3.2.5一元线性回归方程的建立。假设结果枝数与结果量、结果枝数与果实直径、结果量与果实直径的一元线性回归方程为：v=a+bx。

根据参数的最小二乘准则，在R语言程序，植入函数lmO，分别求得a、b的值（表3）。

结果枝数（x）与结果量（Y）的一元线性回归方程为：y=-283.04+62.83x;结果枝数（x）与果实直径（y）一元线性回归方程为：Y=9.42124-0.06184x;结果量（x）与果实直径（y）的一元线性回归方程为：y=9.023579+（-0.0008772x）。

3.2.6显著性t检验。在R语言程序中，植入函数Summary（），分别求得回归方程的判定系数R²、回归系数a的t检验统计量和P值、回归系数b的t检验统计量和P值（表4）。

结果枝数与结果量的一元线性方程Y=一283.04+62.83x的判定系数R²=0.3728427，表明结果量的变动中可以由结果枝数来解释的部分37.28%，未解释的部分62.72%，估计回归方程拟合优度较高;标准误差S=187个，也说明回归方程的平均误差较小，拟合优度较高;回归系数a和b的t检验统计量分别是-1.076和5.342，对应的P值分别为0.287和2.4×10^-6因此在0.05的显著水平下，a和b的t检验都通过。

结果枝数与果实直径的一元线性方程y=9.42124-0.06184x的判定系数R²=0.0790465，表明果实直径的变动中可以由结果枝数来解释的部分7.04%，未解释的部分92.96%，估计回归方程拟合优度一般;标准误差S=0.48cm，也说明回归方程的平均误差中等，拟合优度一般;回归系数a和b的t检验统计量分别是13.83和一2，03，对应的P值分别为2.0×10^-16和0，00307，因此在0.05的显著水平下，a和b的t检验都通过。

结果量与果实直径的一元线性方程y=9.023579-0.0008772x的判定系数R2=0，1684579，表明果实直径的变动中可以由结果枝数来解释的部分16.84%，未解释的部分83.16%，估计回归方程拟合优度一般;标准误差s=0，46cm，也说明回归方程的平均误差中等，拟合优度一般;回归系数a和b的t检验统计量分别是28.182和-3.118，对应的P值分别为2.0×10-16和0.00307，因此在0.05的显著水平下，a和b的t检验都通过。

3.2.7一元线性回归的预测。结果枝数与结果量的一元回归预测，在R语言程序中，分别输入结果枝数x：18、19、20、21、22、23，并植入函数predictO，预测结果量y分别为：847、910、973、1036、1099、1162，并给出一定变动区间（表5）。

结果枝数与果实直径的一元回归预测，在R语言程序中，分别输入结果枝数x：18、19、20、21、22、23，并植入函数predict O，预测果实直径y分别为：8.3、8.2、8.1、8_1、8.0、7.9，并给出一定变动区间（表6）。

结果量与果实直径的一元回归预测，在R语言程序中，分别输入结果枝数x：800、900、1000、1100、1200，并植入函数predictO，预测果实直径y分别为：8.3、8.2、8_1、8.0、7.9，并给出一定变动区间（表7）。

从表6、7、8中可见，结果枝22枝时，测预结果量、果实直径分别为1099个、8.0cm，结果量1100个时，预测果实直径为8.0cm，与实际调查结果的平均结果量1103个相近，与平均果实直径8.0cm相等。

4结论

（1）钦福花场绿叶硬枝型朱砂根盆花的结果枝数、结果量、果实直径的数值呈近正态分布。

（2）结果枝数与结果量存在线性正相关关系，相关系数0.6106085;结果枝数与果实直径、结果量与果实直径存在线性负相关关系，相关系数分别-0.281 1 521、-0.4104362;3个相关系数均通过t检验。

（3）结果枝数（x）与结果量（v）的一元线性回归方程为：y=-283.04+62.83x;结果枝数（x）与果实直径（y）一元线性回归方程为：Y=9.42124-0.06184x;结果量（x）与果实直径（y）的一元线性回归方程为：y=9.023579+-0.0008772x。3个方程的回归系数a、b在95%显著水平下通过t检验，结果枝数与结果量的一元线性回歸方程拟合优度比较高，其它2个的拟合优度一般。

（4）经过一元线性方程预测，结果枝22枝时，结果量、果实直径分别为1099个、8.0cm，与实际调查结果的平均值是相近或相等。

5讨论

（1）结果量与结果枝数存在正相关关系，且相关系数较高，所以，培育特殊花枝对提高朱砂根盆花质量尤为重要。（2）果实直径与结果枝数、结果量存在负相关关系，相关系数较低，说明果实直径的大小更关键的因素在于结果后保果、促果措施，如科学选择肥料、合理施肥等。（3）因为结果枝数、结果量、果实直径之间存在相关关系，在朱砂根盆花生产质量果实数量指标方面，首先要确定一个合理的结果枝数目标值，然后通过栽培措施，提高结果量和果实直径。

（收稿：2019—10—04）