不确定金融市场下具有浮动利率的几何平均亚式期权的定价

王振芳，罗 芳

(山西大同大学数学与统计学院，山西大同037009)

自从 1973 年 Black 和 Scholes[1]，以及 Merton[2]建立了期权定价理论之后，Black-Scholes-Merton 公式已成为期权和其他金融衍生品交易中不可缺少的工具。1997 年，Scholes 和Merton 因这一贡献而获得诺贝尔经济学奖，之后，随机金融理论也得到快速发展。在Black-Scholes的股票模型中，股票价格被描述为一个随机过程，假设股票价格服从几何布朗运动，但是仍有许多学者认为一些股票的价格并非表现为随机性。为了处理非随机性的现象，1965 年，Zadeh[3]建立了模糊集理论，随后，被广泛接受和应用到科学和工程的各个领域。在金融领域，也有大量学者利用模糊集理论研究投资组合和期权定价等问题，如Wu[4]给出了模糊形式的Black-Scholes 欧式期权定价公式，Youshida[5]也研究了在模糊环境下的欧式看涨和看跌期权。

尽管模糊集理论得到广泛接受与应用，但仍有许多学者对此提出挑战，大量研究表明人的信度既不能用主观概率来解释，也无法用模糊集理论来解释。为了合理地处理关于人的信度的问题，在2007年，Liu[6]提出了一种处理信度的新的公理化的数学理论——不确定理论，随之受到许多学者的研究，并在许多领域得到应用与发展，如不确定积分、不确定微分方程、不确定规划、不确定统计、不确定风险分析、不确定金融等。利用不确定理论，Liu[7]提出了一个不确定股票模型，并给出了基于Liu 股票模型的欧式期权定价公式，之后，Chen[8]得到了Liu股票模型下的美式期权定价公式。Zhang和Liu[9]研究了该模型的几何平均亚式期权的定价问题。

在以上模型中，都假定利率为常数，这一假设忽视了利率随时间变化的事实。2013 年，Chen 和Gao[10]基于不确定理论假设利率服从一个不确定过程，给出了一个不确定利率模型。对不确定利率下的几何平均亚式期权进行了研究，并得到了相应的期权定价公式。

1 预备知识

当没有足够的样本数据时，人们往往会用专家的信度来作出判断，在这种情况下，概率论难以作出很好的刻画，不确定理论的提出，成为一种研究这类不确定现象的数学系统。

对需要用到的一些不确定理论的概念和性质做一介绍：

定义1令 Γ 是非空集合，L是 Γ 上的σ代数，σ代数L中的每个元素Λ 称为事件，不确定测度M是从L到[0,1]的函数，满足如下公理：

公理1对全集Γ，M{Γ}=1。

公理2对任意事件 Λ ，M{Λ}+M{ΛC}=1。

公理3对任何可列事件Λ1，Λ2，…，有

分别称为规范性，对偶性和次可列可加性。

定义2令 Γ 是非空集合，L是 Γ 上的σ代数，M是不确定测度，则三元组(Γ，L，M)称为不确定空间。

Liu[7]在2009年定义了乘积不确定测度，也就是不确定理论的第四公理。令(Γk，Lk，Mk)

k=1,2,…，是不确定空间，记

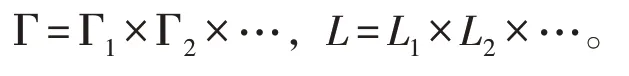
公理 4令 (Γk,Lk,Mk) ，k=1,2,…，是不确定空间，不确定乘积测度满足

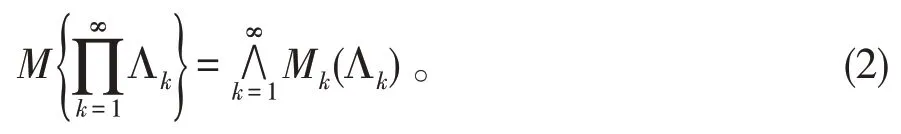
这里Λk是Lk中任意选取的事件，k=1,2,…。

定义3不确定变量ξ是从不确定空间(Γ,L,M)到实数集的可测函数，即对任意的Borel集B，集合

是L中的事件。

定义4不确定变量ξ的不确定分布定义为

定义5一个不确定分布Φ，如果对于每一个α∈(0,1)，它的反函数Φ-1(α)存在且唯一，则称之为正则不确定分布。

定义6设ξ是一个具有正则不确定分布Φ的不确定变量，逆函数Φ-1被称为ξ的逆不确定分布。

定义7如果不确定分布为

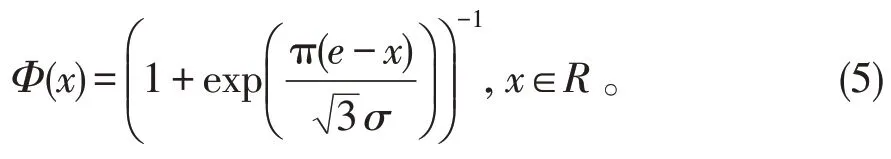
则不确定变量ξ称为正态不确定变量，记为N(e,σ)，这里e和σ是实数且σ＞0 。

它的逆不确定分布是

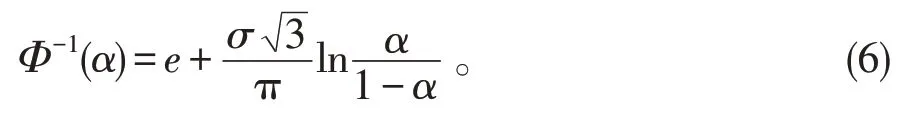
定义8令ξ是不确定变量，则ξ的期望值定义为：

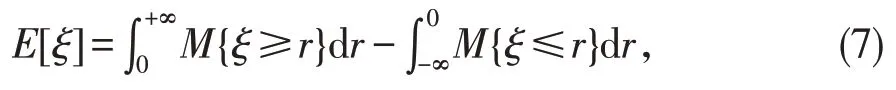
如果上述两个积分中至少一个有限。

定义9如果T表示时间，(Γ,L,M)是一个不确定空间，那么一个不确定过程就是从T×(Γ,L,M)到实数集的可测函数，即对于任意的时间t∈T和Borel 实数集B，{Xt∈B}={γ∈ Γ|Xt(γ)∈B}是L中的事件。

定义10Liu 过程Ct是指满足下面三个条件的不确定过程：

(1)C0=0，几乎所有的轨道Lipschitz连续；

(2)Ct具有独立稳态增性质；

(3)对于时间t，增量Cs+t-Cs是一个具有期望为0和方差为t2的不确定变量，其不确定分布是

Liu[7]过程是一类特殊的不确定过程，它的样本轨道函数不可微点虽然稠密，但却是Lipschitz 连续的。

定理1令ξ是不确定变量并且具有不确定分布Φ，如果期望值存在，则

定理2令ξ是不确定变量并且具有正则不确定分布Φ，如果期望值存在，则

定理3令ξ1,ξ2,…,ξn是独立的不确定变量并且具有正则不确定分布Φ1,Φ2,…,Φn，如果函数f(x1,x2,…xn) 对x1,x2,…xm严格单增，对xm+1,xm+2,…xn严格单减，则ξ=f(ξ1,ξ2,…,ξn)是不确定变量并且具有逆分布

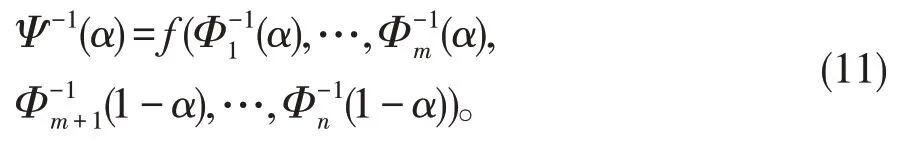
Liu和Ha[13]证明了不确定变量

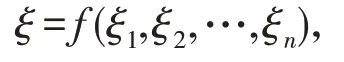
有期望：

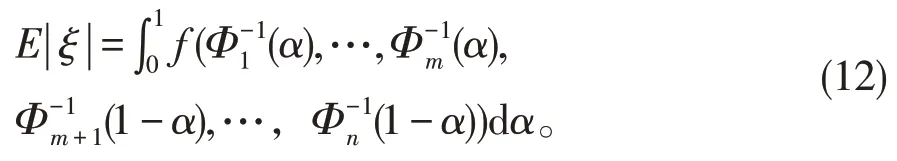
定理4令Xt和是不确定微分方程

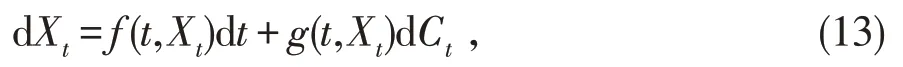
的解和α轨道，那么对任何s＞0 和严格单增函数J(x)，(Xt)dt有逆不确定分布

定理5令Xt和是不确定微分方程

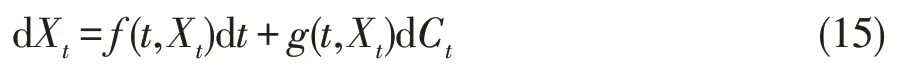
的解和α轨道，那么对任何s＞0 和严格单减函数J(x)，有逆不确定分布

2 具有浮动利率的不确定股票模型

1973 年，Black 和 Scholes 在假设股票价格服从几何布朗运动的前提下，给出了著名的欧式看涨期权的定价公式。其股票模型如下：

其中Xt为债券价格，r为无风险利率，St为股票价格，μ为期望回报率，σ为波动率，Bt为Wiener过程。

2009年，Liu[7]依据不确定理论假定股票价格服从几何Liu过程，提出如下的股票价格模型：

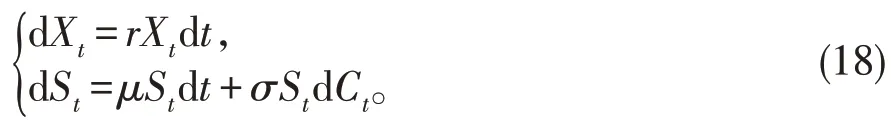
其中Xt为债券价格，r为无风险利率，St为股票价格，μ为期望回报率，σ为波动率，Ct为Liu过程，并给出了相应的欧式期权的定价公式。

以上模型都假定利率为常数，忽视了利率随时间变化的事实。2013 年，Chen 和Gao[10]基于不确定理论假定利率服从一个不确定过程，给出了如下的不确定利率模型：

其中a,b和δ都是常数。

将基于如下的股票价格模型来研究几何平均亚式期权的定价问题：

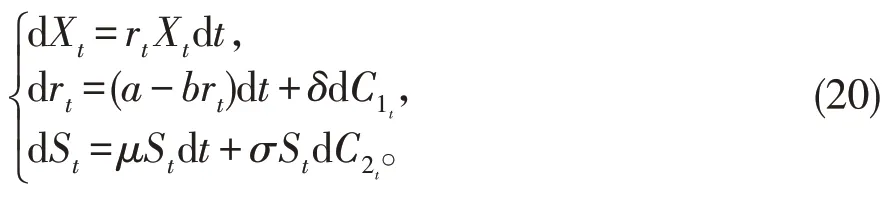
其中Xt为债券价格，rt为不确定利率，St为股票价格，μ为期望回报率，σ为波动率，C1t和C2t为两个相互独立的典范过程，rt和St独立。

注意到股票价格

它的逆不确定分布是

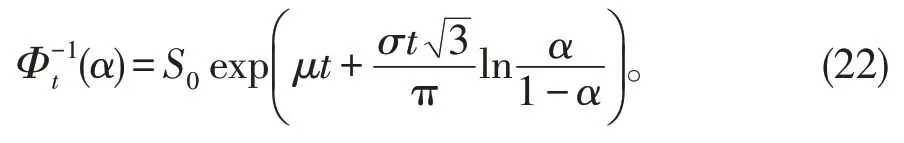
3 具有浮动利率的几何平均亚式期权的定价公式

亚式期权是重要的期权之一，它依赖于路径，由于其良好的风险管理的功能而被投资者广泛接受。亚式期权分为算术平均亚式期权和几何平均亚式期权，主要是研究几何平均亚式期权的定价问题。假设亚式期权在到期时间T有敲定价格K，St是t时刻的股票价格。那么几何平均亚式看涨期权的得益是

考虑到金钱的时间价值，这份得益的当前值应该是

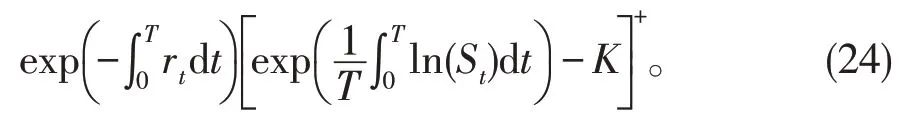
因此亚式看涨期权的价格应该是此得益的平均值。

定义11假设一份几何平均亚式看涨期权具有敲定价格K和到期时间T，那么期权具有价格

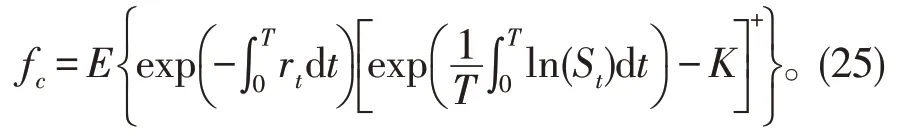
定理6对于股票价格模型20，如果几何平均亚式看涨期权具有敲定价格K和到期时间T，那么期权的价格是

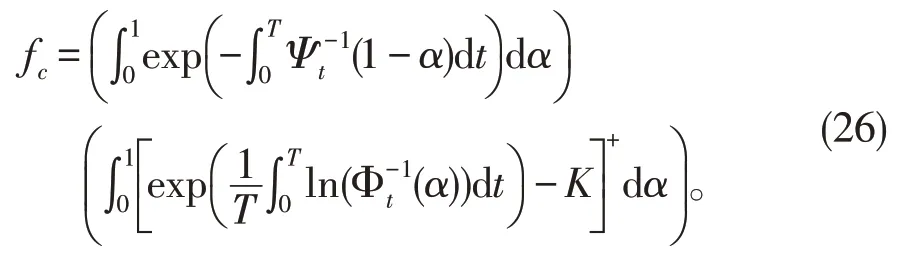
其中

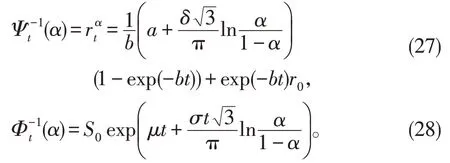
证明由rt和St的相互独立，我们有

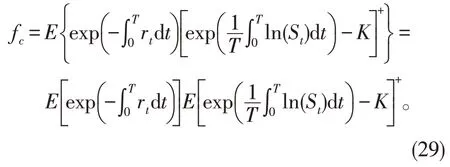
解微分方程

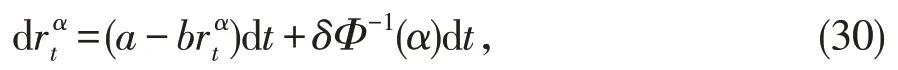
其中 0 ＜α＜1，Φ-1(α)是逆标准正态不确定分布，从而有

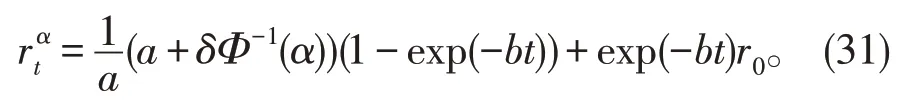
这意味着不确定微分方程

有α轨道

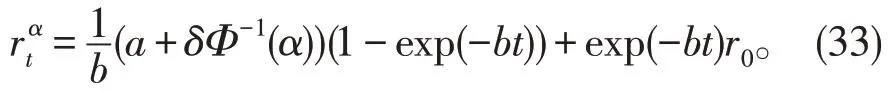
根据Yao-Chen公式可知rt有逆不确定分布

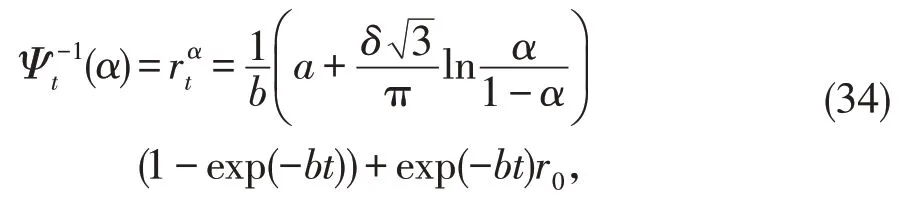
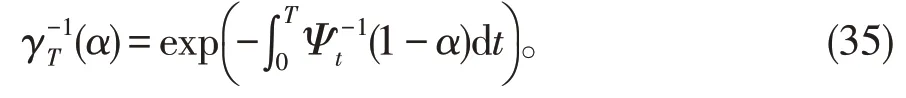
那么我们有

由定理3和式(22)可知

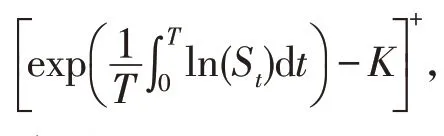
有逆不确定分布

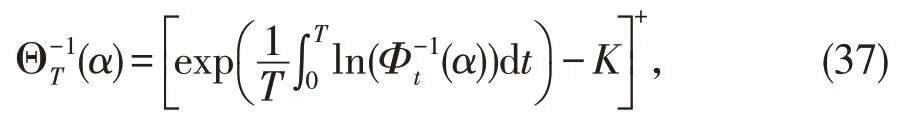
其中

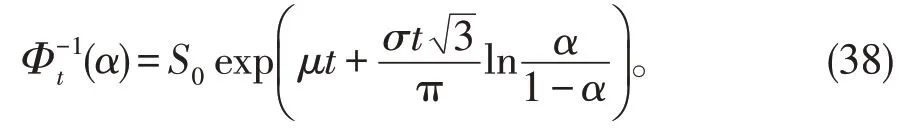
因此

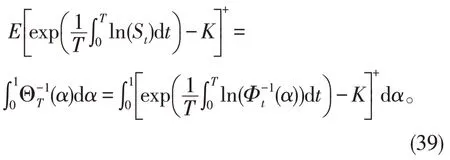
所以几何平均亚式看涨期权的价格为

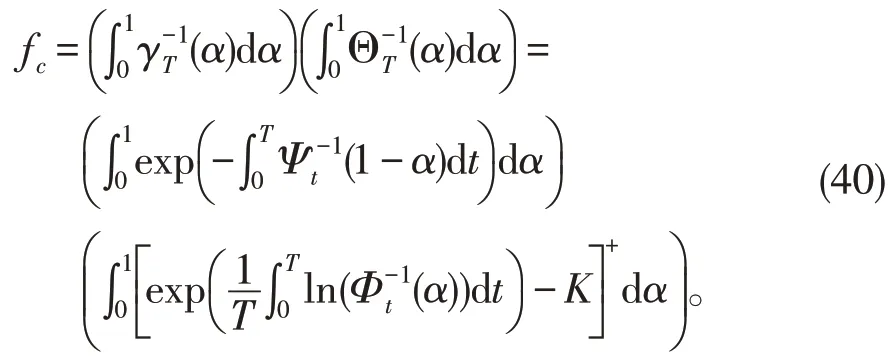
定理证毕。

同理我们给出如下的几何平均亚式看跌期权的定价方式：

定义12假设一份几何平均亚式看跌期权具有敲定价格K和到期时间，那么期权具有价格

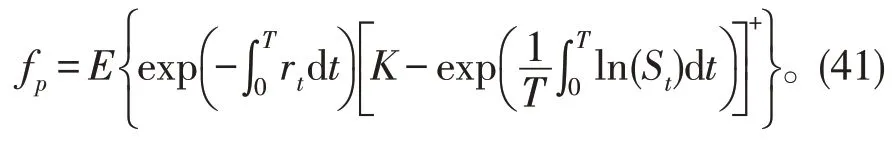
定理7对于股票价格模型(20)，几何平均亚式看跌期权具有敲定价格K和到期时间T，那么期权的价格是

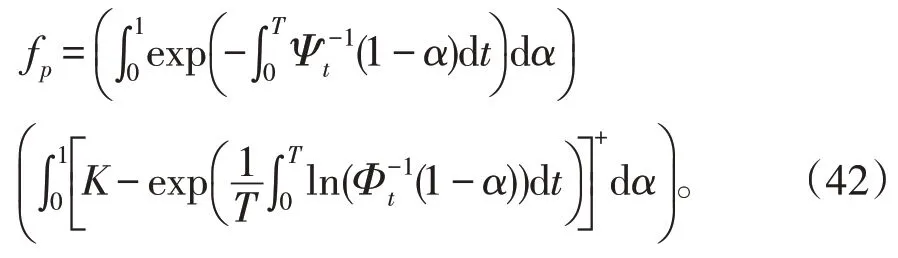
其中

证明根据定理5，类似于定理6的证明，我们可以得到亚式看跌期权的价格为

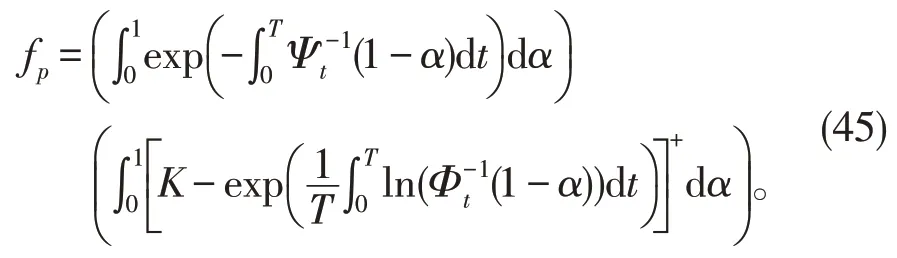
定理证毕。

4 结论

期权定价是现代金融中最重要的内容之一，经典的期权定价理论是建立在概率论的基础之上，认为金融市场具有随机性，假设股票价格服从几何布朗运动，利用随机微分方程得到了期权定价公式。但是Liu给出的悖论表明用随机微分方程描述股票价格变化过程并不合适。在不确定理论基础上，利用不确定微分方程来描述股票价格变化和利率期限结构，研究了具有浮动利率的几何平均年亚式期权的定价问题，并给出了相应的定价公式。