模糊模式识别法标度软硬酸碱理论中碱的软硬度

多本加

(青海省藏语佛学院，青海贵德811700)

现代化学是一门信息量巨大的学科。描述化合物的种类和数量所涉及的数据信息可以描述为一个巨大的数据海洋，如何利用数学方法从大量的数据信息中提取有用的信息，并发现化学规律，已成为基础化学研究的热点之一。我们考虑了许多物理化学性质，如硬酸和软酸、强碱和弱碱等的概念[1-3]，其外延是模糊的，应用模糊数学方法建立了酸碱软度的数学模型，并将其应用于酸碱软度的分类和预测，结果令人满意。

1 建模原理

1.1 化合物的隶属函数

设A1，A2, …,An是论域U中的n个模糊子集，U=R(实数)，具有以下形式的隶属函数：

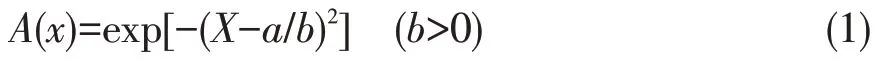
键参数a、b分别为电负性（X）和离子电荷半径比(Z2/R)[4-6]。

1.2 择近原则

设模糊集合A1、…、An，B∈U；若存在1 ≦i≦n，使得

则认为B与Ai最贴近，即判定B与Ai为一类。

1.3 贴近度的计算

设A、B是U上的两个模糊子集,记

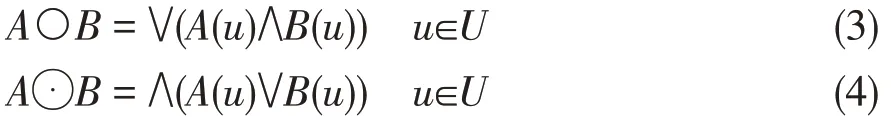
符号“∨”和“∧”分别表示最大值和最小值，A○B为模糊子集A与B的内积，A⊙B为模糊子集A与B的外积，A(u),B(u)为隶属函数，定义：记(A,B)=1/2(A○B+(1-A⊙B)),若A1，A2模糊子集,分别具有参数(a1,b1),(a2,b2),则有：

如果2 个模糊子集的贴近度趋于1，则两个模糊子集越接近[7]。

2 酸碱软硬度的判别

取6 个类别的化合物作为模型,它们分别是A1(硬酸)、A2(交界酸)、A3(软酸)、B1(硬碱)、B2(交界碱)、B3(软碱)。其键参数a、b的取值见表1。

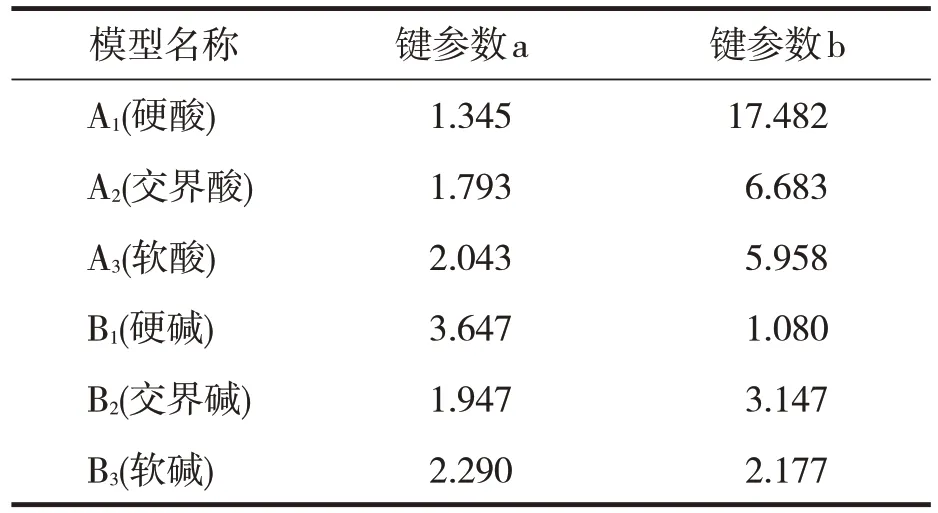
表1 各模型键参数取值

根据表1、2和3的数据，采用等式(5)计算每种化合物与3类已知化合物的贴近程度，然后根据择近选择度确定归属。下面的例子说明了酸碱硬度判别方法。已知化合物C=Rb+的a= 0.68,b= 0.8则根据方程式(5)，要识别的模型c 和已知的3 个模型的贴近程度计算为：

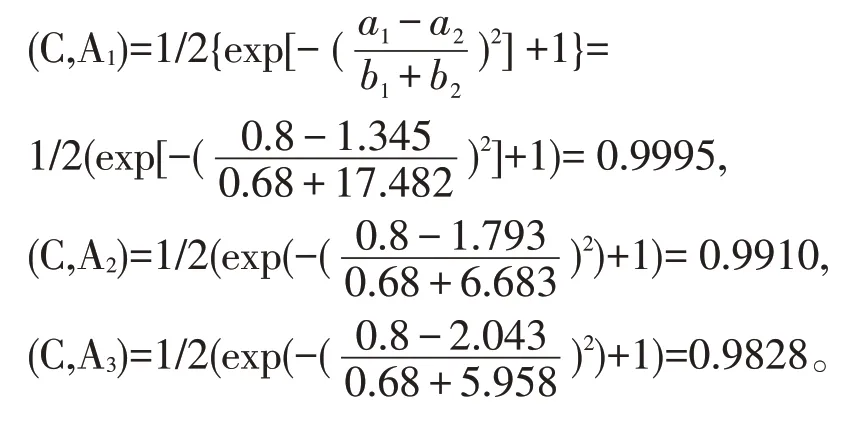
按择近原则可判定, Rb+∈H(硬酸), Rb+为硬酸,这与已知的实验结果是一致的。出于同样的原因，可以计算剩余化合物与已知模型的贴近度。相关数据及判别结果见表2。

3 结果与讨论

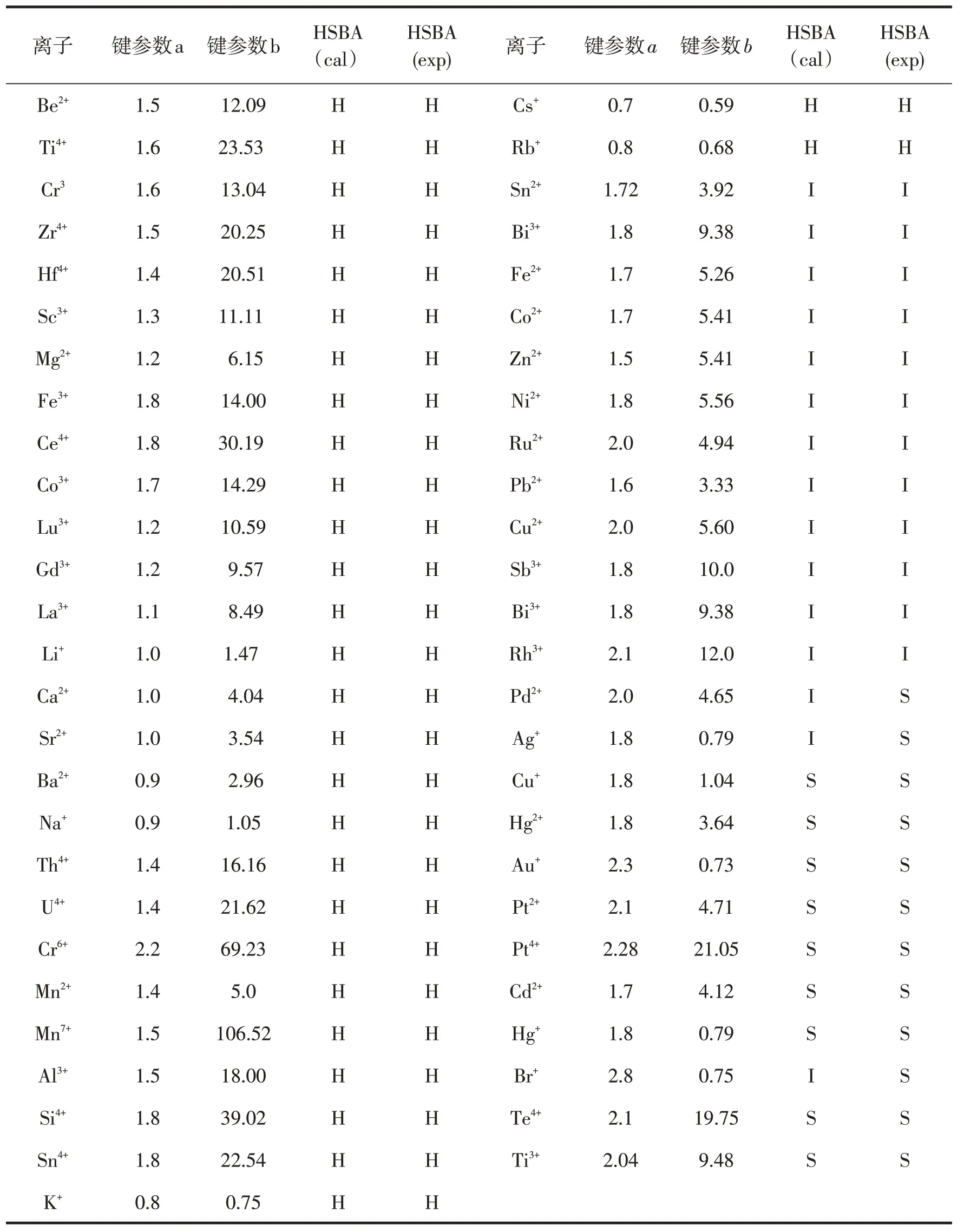
表2 常见离子的有关数据及判别结果

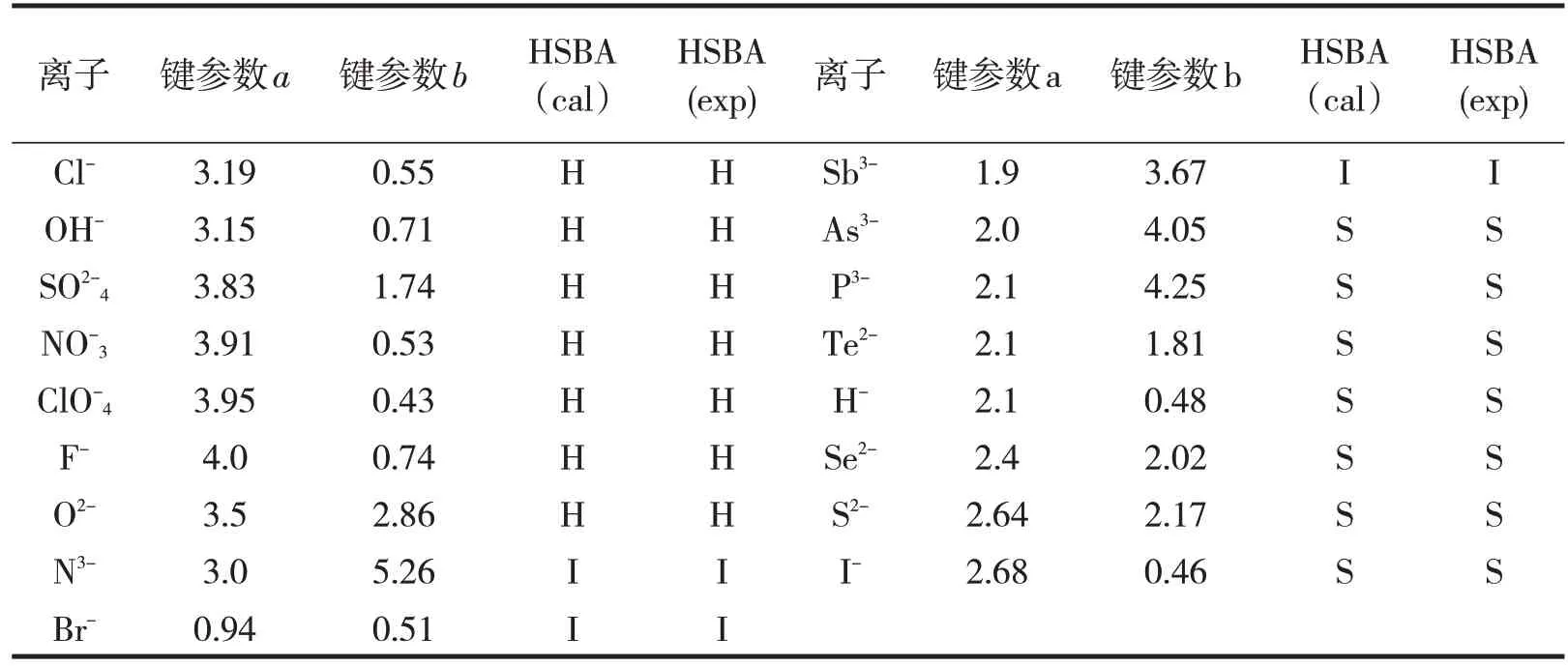
表3 碱的软硬度的键参数标度值

我们选择电荷半径比和电负性差作为两个基本参数来区分酸碱硬度，物理意义是明确的,酸和碱的硬度表示酸和碱所持电子的紧度[10]。因此，测量酸碱硬度的参数应充分反映酸碱相互作用过程中的抓电子的能力，电负性可以作为尺度参数，因为它与粒子吸引外层电子和抵抗电子损失的能力有关。此外，极化直接反映了电子抓取的紧密性，Z2/R的值可以作为离子极化能力的度量。故本文选用标度参数之一，这恰与我们所得的结论一致，即化合物的键型不是绝对的概念。一个正常化学键是非极性共价部分和强极性离子部分的线性组合,正常键的类型取决于哪个键占优势[11]。因而,像离子性和共价，酸度和碱度、离子软度和硬度也是一对模糊的概念。因此，应用模糊数学方法研究其分类是可行的。在本文中所建立的类型判别模型,识别率在96%以上，达到了一般的模式识别方法的识别水平。