连锁便利店分档研究

陶 浩，吴 旦，田考聪

（重庆医科大学,重庆400016）

一、导言

随着信息化的不断发展，连锁便利店已经成为当前社会便利销售服务的核心。中国连锁经营协会与波士顿咨询公司联合发布的 《2017年中国便利店发展报告》指出，我国2017年便利店行业增速达23%，门店超过10万家，市场规模超过1900亿元。开店数量及门店销售额双双增长，市场空间大，一二线城市是增长热点①。

但看似欣欣向荣发展的背后，却存在着巨大的危机。一方面，本土便利店品牌会直接遭遇外资品牌在综合运营能力上的挑战；另一方面，自身的品牌建设能力和商品开发能力不足，导致企业缺乏明确的价值观和落地能力②。近年来店铺租金、人工成本的不断上涨也给企业带来更多负担。不少连锁便利店不仅难以盈利，甚至连维持生计也成为问题。目前对连锁便利店的研究主要包括在选址、竞争策略、品类管理、配送优化等方面。很少有学者从门店自身产生的大量销售数据入手，对企业的发展和管理提出建议和给予帮助。本文对X市Y便利店的经营数据进行分析，现将结果进行报告。

二、对象与方法

（一）对象

本研究取自于X市Y连锁便利店的150家门店2017年6月至2018年5月的销售数据,主要信息包括交易时间、流水号、子店名称、商品名称、购买数量、销售额、商品成本、商品毛利润等，共计6145万余条销售记录。

对企业而言，开设便利店的目的是盈利，因此本文的研究对象是各门店的每日毛利润。考虑到便利店的每日毛利润易受到休息日、节假日等的影响，选择其毛利润的变异系数作为稳定性的衡量。日均利润越高，说明该店的运营能力越强；变异系数越低，说明该店的经营越稳定。经提取每家店每日毛利润，剔除异常值，求其平均值后，得到最终的数据集如表1所示。

表1 各店日均利润及其变异系数

（二）方法

1.基于熵权的TOPSIS综合评价。熵权是根据各指标观测值的信息量（熵）来计算权重的一种客观赋权方法。它能够客观体现决策时某项指标在指标体系中的重要程度③。基于熵权的TOPSIS法的计算步骤如杜挺和李灿等所论④⑤。用TOPSIS法进行评价，转化方式用倒数法⑥。然后对同趋势化后的原始数据矩阵进行归一化处理：

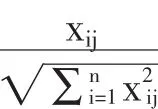
确定最优方案（Z+）与最劣方案（Z-）：

采用熵权权重模型，计算权重。

首先，计算各指标的熵

再计算各指标的差异系数dj:

式中，dj越大，说明该指标越重要。最终计算出各指标的权重wj：

在上述基础上计算出Ci。

按照Ci大小将各评价对象排序，Ci值越大，表示综合效益越好。

（三）有序样品聚类

有序样品聚类由Fisher于1958年提出，它对样品进行分类时，要求考虑样品的顺序特性这个前提条件，不破坏样品间的顺序。具体的分析步骤为③⑦：

步骤 1：设样品 X1、X2、…、Xn在分档中，某类 G 包括的样本有{Xi、Xi＋1、…、Xj}，(j＞i),则该类的均值向量为：

将该类内部的各样本间的总差异（其指标是离差平方和）定义为该类的直径，用D（i,j）表示：

步骤2：定义此分类的最小损失函数即为类内总离差平方和:

步骤3：确定聚类个数：最优分割就是使L[p(n,k)]达到最小值的一种分类法，聚类个数通过做L[p(n,k)]与聚类数k的变化趋势图求得，曲线的拐点处即为最优聚类个数⑧。

（四）分类决策树

决策树常用的算法有ID3、C4.5与CART⑨。本文是基于连续属性来生成决策树，因此使用C4.5算法，它的采用机制是用二分法对连续属性进行处理。从根节点开始，选取最优分割点来进行样本集合的划分，使其该点二分后的信息增益达到最大。再对子节点递归的调用以上方法，构建决策树，直到所有特征的信息增益均很小或没有特征可以选择为止⑩。

三、结果

（一）基于熵权的TOPSIS法评价

现对表1中150家门店进行综合评价。日均利润、变异系数作为原始指标，属于权重未知的情况，故采用熵权法求得日均利润与变异系数的权重分别为：0.79217、0.20783。确定权重后，进行TOPSIS综合排序。其排序部分结果如表2所示。

表2 150家门店基于熵权的TOPSIS法排序结果

（二）有序样品聚类

上述中的C值作为综合指标，表示为诸评价对象与最优方案接近程度。是综合考虑了各子店的日均利润、变异系数而计算出的值。虽然可以直观地看到每家门店经营能力在连锁品牌中的排位，但是本研究旨在对150家门店进行分档，即把运营实力相近的门店放到相同的档位。现利用有序样品聚类法对TOPSIS法中的C值进行聚类。主要结果如表3所示。

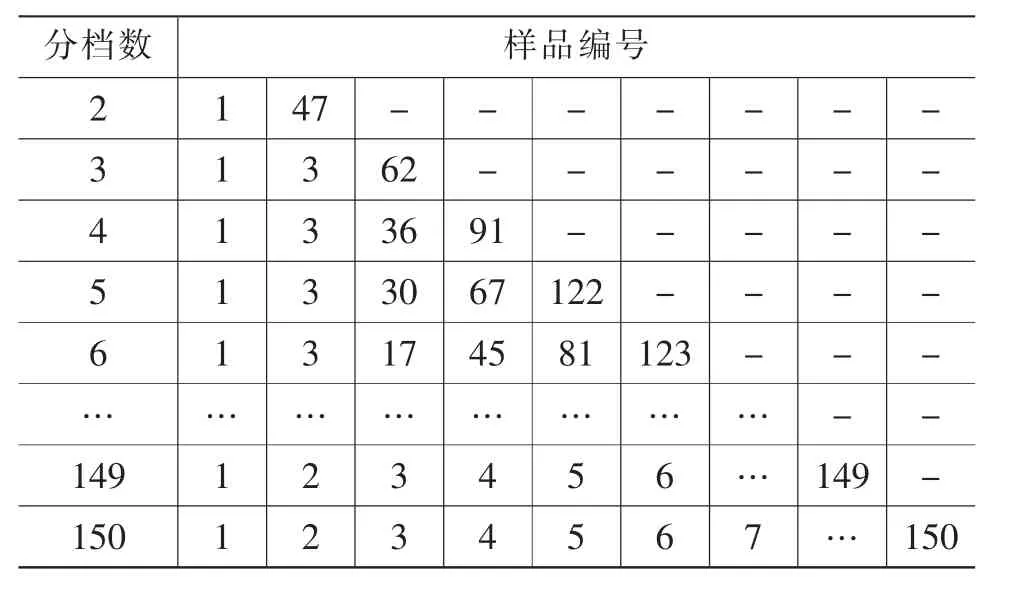
表3 有序样品聚类结果

图1为聚类数K（只取到20）与其最小损失函数值的变化趋势图。曲线的拐点出现在K=6时，说明有序样品被分为6档时效果较好。此时，最小损失函数值为0.144。结合表3可知，第一档门店：2家；第二档门店：14家；第三档门店：28家；第四档门店：36家；第五档门店：42家；第六档门店：28家。各子店的具体分档情况如表4所示。

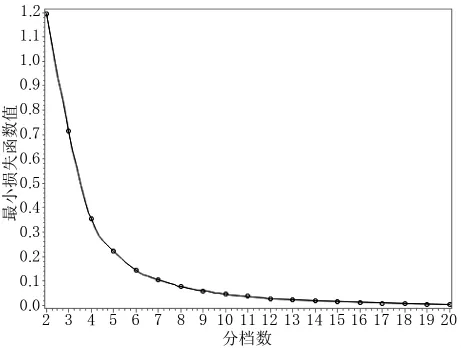
图1 不同分档数时的最小损失函数值

表4 150家门店的分档结果

现对各档位门店日均利润的均值是否相同做差异性分析。由于第一档的门店数仅有两家店，样本过少，在此不纳入分析。Shapiro-Wilk检验结果表明，剩下5个档位门店的日均利润数据均满足正态性分布。而Levene方差齐性检验结果为F=1.64，P=0.1667＞0.05，表明这五组的数据满足方差齐性。故在此可采用方差分析对各组间的均值进行比较。其结果如表5所示。

表5 各档日均利润方差分析

方差分析结果为F=518.82，P＜0.0001，说明各档位门店的日均利润均数存在统计学差异，SNK-q检验两两比较结果表明：任意两个档位之间的差异均具有统计学意义。具体均数的高低为：Ⅱ档(均数：3348.28)＞Ⅲ档 （均数：2560.13）＞Ⅳ档 （均数：1832.62）＞Ⅴ档 （均数：1227.61）＞Ⅵ档 （均数：623.32）。这说明有序样品聚类进行分档的结果比较合理，能够将运营实力相近的店面放到同一档位，不同档位间具有明显的差异。

（三）决策树分类

经过综合评价和有序样品聚类，不仅实现了150家子店的综合经营实力排序，而且对其完成了所处档位的标注。而企业管理者较关心的一个问题是原始指标的阈值具体为多少时，子店可以分到何等档位。现运用机器学习中的分类决策树对表6进行分类学习，以便能实现其需求。

表6 150家门店的原始指标及其档位标注

由于该连锁品牌中子店属于Ⅰ档的门店仅有两家，这在决策树中分成训练数据集和验证数据集会造成一定的影响，因此在上表的等级一列中，其值的意义为：2（Ⅰ、Ⅱ档）、3（Ⅲ档）、4（Ⅳ档）、5（Ⅴ档）、6（Ⅵ档）。分别代表门店的等级：优、较优、良、中、差。即将样本较少的档位合并到邻近的低档位中，便于决策树的学习以及泛化效果的验证。其模型的部分结果如图2所示。

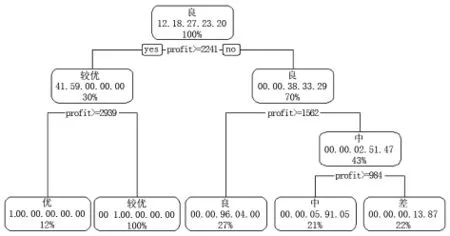
图2 基于信息增益生成的决策树

将表6中的150家门店随机分为训练样本与验证样本，其比例为7:3。由训练样本最终生成的决策树如图2所示，一共有四次分叉，且均用了日均利润这个变量。其4个划分节点分别为2939、2241、1562、984。 表明门店其日均利润在[2939，＋∞＋∞）区间时被分为优店；在[2241,2939）时被分为较优店；在[1562,2241）区间时大可判断为良店；在[984,1562）区间时可判断为中等店；在[0,984）区间时可判断为差店。其生成的决策树在验证集上的预测准确率为91.11%，其分类准确率较高，具体的分类结果（混淆矩阵）如表7所示。

四、总结与建议

便利店作为一个竞争极其残酷的行业，若企业没有系统性地对自身进行评估和认识，很难做出理性决策来帮助自身在市场上立足。本文建立了一套连锁便利店全面的合理性评价细则。综合考虑便利店的运营能力和稳定性，选取各子店的日均利润和变异系数来作为原始指标,进行基于熵权的TOPSIS综合评价。可得到具体门店在其所有店面中的经营实力排名，这可以帮助企业管理人员直观地看到各门店的综合运营能力高低。

表7 生成决策树对门店的预测结果

通过有序样品聚类，可以有效地将所有店面划分为6个不同优劣等级的档位，相同档位内的门店经营能力比较接近。其中极优店面有2家，占比1.33%；较优店面有14家，占比9.33%；良好门店有28家，占比18.67%；中等门店有36家，占比24%；较差门店有42家，占比28%；而极差门店有28家，占比18.67%。总体看来，该连锁便利店只有不到30%的优良门店，其经营状况亟待改善。

运用决策树进行分类学习表明，不仅帮助企业确定了不同档位间的分档阈值，可以让子店的运营者了解到自身经营水平属于何种等级；而且该决策树的泛化能力比较强，对新店的经营水平可直接进行预测。在此，本文可以有效地对国内连锁便利店进行高效分档，并确立其分档指标的阈值大小，可以为企业的政策制定与调整提供有效参考。

最后，建议企业从以下两个方面做出改善。首先，对所有店面的位置进行综合评分，在这里可以参考便利店选址模型。通过地址评分，一方面可以找出位置评分低而自身经营能力也很低的门店，可以直接考虑关店，及时止损。另一方面，可以找出位置评分高但自身经营能力却很低的门店，必须关注这部分地理位置上的优质门店，及时找出其经营能力不强的原因，进行调整。其次，该连锁品牌子店分布于该市各区，可以对其进行地址划分，结合其划分区域门店优良占比情况，合理选择建仓位置及其大小，在满足门店经营需求下，最大程度地降低运输成本和储存成本。

注释：

①中国连锁经营协会，波士顿咨询公司.2018中国便利店发展报告[EB/OL].（2018-05-24）[2018-08-05].http：//www.ccfa.org.cn/portal/cn/view.jsp?lt=33&id=434758.

②章曼程.我国连锁便利店发展存在的问题及对策分析[J].时代金融,2016.

③毛玮.几种典型综合评价方法的比较及SAS软件实现[D].中国人民解放军军事医学科学院,2011.

④杜挺,谢贤健,梁海艳等.基于熵权TOPSIS和GIS的重庆市县域经济综合评价及空间分析[J].经济地理,2014,34(6):40-47.

⑤李灿,张凤荣,朱泰峰,等.基于熵权TOPSIS模型的土地利用绩效评价及关联分析[J].农业工程学报,2013,(5):217-227.

⑥孙振球.医学统计学[M].北京：人民卫生出版社，2016:416-417.

⑦颜虹.医学统计学[M].北京：人民卫生出版社，2010:416-417.

⑧蔡亚宁,裴晓婷,孙盼盼等.基于有序聚类分析法探讨成年人体质指数的年龄和性别分布特征[J].中华流行病学杂志,2018,39(6):821-825.

⑨李航.统计学习方法[M].北京：清华大学出版社，2018:55-74.

⑩周志华.机器学习[M].北京：清华大学出版社，2018:79-88.