基于多假设解分离算法的BDS/SINS紧组合完好性监视

王海东1,孙淑光,匡 杉

(1.大连国际机场，辽宁 大连 116033; 2.中国民航大学 电子信息与自动化学院，天津 300300)

0 引言

民航PBN运行要求卫星导航接收机必须具备接收机自主完好性监测(receiver autonomous integrity monitoring，RAIM)功能。RAIM算法利用冗余卫星信息进行完好性监视，在存在一颗卫星故障的情况下，要求接收机接收到的卫星(高度角5°以上)数量至少5颗及以上才能进行故障卫星的检测，而要进行故障卫星的隔离则至少需要不少于6颗可见星。当飞机在更高精度要求的环境下运行时(如精密进近阶段等)，为确保导航精度，部分测距误差较大的卫星也可能被认为是故障卫星而进行隔离，这就会出现多故障卫星同时并存的情况，这种情况下，要进行故障的检测与隔离，必然需要更多的可见星信息。SINS作为飞机的重要导航系统，与卫星导航系统进行紧组合导航计算，BDS已经在2018年12月26日完成了基础性全球卫星的布网，在95%时间运行情况下，水平准确率达到10 m，因此BDS/SINS的组合，不仅可以增加系统的冗余信息，而且由于利用SINS高度和地球半径信息，将地球作为紧组合算法中的一颗伪卫星，可以有效改善组合导航的几何精度因子(geometric dilution precision,GDOP)，提高定位精度。

BDS/SINS组合导航可以实现二者的优势互补，更好地满足导航精度和带宽等方面的要求。BDS观测量对SINS的误差漂移有一定抑制作用，而SINS可以改善BDS导航的连续性和完好性。民航飞机上通常有三套SINS，可以利用三个SINS信息对SINS进行组合前的设备故障预检测，如果有设备故障，则首先将故障设备隔离，然后利用正常设备的位置信息进行组合导航的计算，如果设备没有故障，则可以利用三套SINS设备输出的加权平均值进行组合导航的计算，确保组合导航的精度。考虑到对机载三套SINS的适航要求，在BDS/SINS紧组合导航计算中，可以忽略SINS故障的情况，而仅进行故障卫星的检测与隔离。

1 BDS/SINS紧组合方式

误差的存在会降低系统的导航精度，从而影响到导航的完好性。BDS接收机的误差主要有随机误差、非随机误差和外来误差三类。各种误差来源和性质明显不同，其中随机误差主要和传输以及接收机自身性能有关；非随机误差主要有传输延迟、多径误差、钟漂等，此类误差会影响伪距测量精度。可基于误差模型来修正前两种延迟。而钟漂误差则可通过定位解算来确定；外来误差主要和系统异常有关[2]。

SINS的误差主要包括惯性测量单元(inertial measurement unit，IMU)传感器误差、初始对准误差、计算误差以及各种干扰引起的误差等[3]。传感器误差主要包括陀螺和加速度计的常值误差、漂移和标度因数等导致的误差。具体分析可知，其中初始对准误差主要包括初始对准的位置、速度和姿态误差，组合导航中，主要受KALMAN滤波器的影响。计算误差主要包括SINS计算的量化误差、累积误差以及参数设置误差。干扰误差主要是飞机受到冲击或震动时的误差。

1.1 BDS/SINS组合导航系统误差分类

虽然BDS/SINS组合导航系统的误差种类众多，但根据其特性，基本上可以分为6类[3-5]：

1.1.1 阶跃误差

f(t)=Au(t-t0)

(1)

其中:A为误差幅值；u(t)为单位阶跃函数；t0为起始时间。这种误差较大时，易用“快照”式的完好性监视算法检测到[24]。部分导航偏差可以认为是长时间的阶跃误差，通常在导航解算中考虑消除。

1.1.2 斜坡误差

斜坡误差为一类随时间逐渐变化的误差，其误差模型为：

f(t)=R(t-t0)u(t-t0)

(2)

其中:R为误差斜率；u(t)为单位阶跃函数；t0为误差初始时间。由于误差是逐渐变化的，斜率较小时(即慢变误差)较难检测。若采用“快照”式RAIM算法，只有当误差累积到一定程度时，才可能检测出[4]，设备老化可能产生此类故障。

1.1.3 随机噪声

随机噪声误差较多，从电离层闪烁和对流层变化到SINS解算的各个过程都存在[24]。其误差模型为：

f(t)=Aku(t-t0),

(3)

其中:N(m，V)为高斯正态分布，m为均值，V为协方差；η为误差均值；u(t)为单位阶跃函数；t0为起始时间。

1.1.4 随机游走

随机游走误差主要存在于SINS传感器，各种类型的陀螺和加速度计中，其误差模型为：

(4)

其中:a(t)为高斯分布随机变量；u(t)为单位阶跃函数；t0为起始时间。

1.1.5 振荡误差

振荡误差为SINS的误差类型，主要和SINS的惯导解算与误差校正存在相关性[24]。可通过如下模型描述此误差：

f(t)=Asin(t-θ)u(t-t0)

(5)

其中:A为故障幅值；θ为相位；u(t)与t0含义同上[24,28]。

1.2 运用卡尔曼滤波的BDS/SINS紧组合

BDS/SINS紧组合方式下，相应的输入信息为BDS伪距域观测量，并综合相应的SINS输出信息，而实现组合导航的目的[6]，如图1所示。

BDS/INS紧组合将BDS接收机导航计算和BDS/SINS组合导航算法合二为一，输入参数包括伪距、伪距率，组合系统解算时应用到卡尔曼滤波器。使用扩展卡尔曼滤波器，将BDS接收机观测得的伪距、伪距率与飞机位置、速度之间的关系方程线性化[2]。

1.2.1 系统状态方程

紧组合方式中，卡尔曼滤波器的系统状态方程包括SINS和BDS的误差方程。

在地球坐标系下建立SINS的误差状态方程。状态向量包含位置误差、速度误差、姿态角误差以及加速度计和陀螺的误差，陀螺和加速度计误差只考虑常值漂移误差。

X(t)=[δrx,δry,δrz,δvx,δvy,δvz,δφx,δφy,

δφz,bgx,bgy,bgz,bax,bay,baz]T

其中:下标x、y、z代表在地球坐标系的三个轴向；δrx，δry，δrz为位置误差；δvx，δvy，δvz为速度误差；δφx，δφy，δφz为姿态角、航向角误差；bgx，bgy，bgz为陀螺常值漂移；bax，bay，baz为加速度计常值漂移；wgx，wgy，wgz为载体坐标系下陀螺的噪声；wax，way，waz为载体坐标系下加速度计的噪声[6-8]。

(6)

由SINS的解算方程可得系统的状态转移矩阵为：

WB(t)=[wgxwgywgzwaxwaywax]T

美国国立卫生研究院建立了分工明确、责任可查、合作协调的管理制度，保障基金资助管理水平。一是分阶段管理，美国国立卫生研究院科学评审中心主要负责申请的受理与分配、大部分竞争性项目的初评工作，美国国立卫生研究院各研究所负责二审及项目立项和过程管理。二是管理队伍分工明确，团队协作。美国国立卫生研究院各研究所项目管理人员负责日常管理、审核申请是否符合规章制度和指南；项目官员负责指南编制、审核项目进展报告、现场检查等；项目管理人员、项目官员及财务、临床实验专业管理人员组成科研管理团队，相互配合，充分发挥专业化管理的优势和效率。

BDS接收机设置的状态向量为和接收机时钟对应的误差，主要包括等效距离变化率误差和等效距离误差(分别表示为δtru，δtu)，在分析时前者可看作为一阶马尔科夫过程。可通过如下方程描述这两个误差：

(7)

其中:βtru为相关时间，wtu，wtru为白噪声[9-10]。

因此，BDS接收机误差的状态方程为：

(8)

式中,

式(6)、(8)合并即可得BDS/INS紧组合卡尔曼滤波的系统状态方程：

(9)

即：

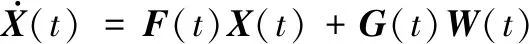
(10)

X(t)=[δrx,δry,δrz,δvx,δvy,δvz,δφx,δφy,δφz,bgx,

bgy,bgz,bax,bay,baz,δtu,δtru]T

1.2.2 系统量测方程

(11)

将上式在(x，y，z)处泰勒展开，舍弃高阶项，得：

(12)

式中,

第i颗卫星与用户的惯导位置之间的距离为：

ρIi=ri+ei1δx+ei2δy+ei3δz

(13)

BDS接收机观测得的接收机到第i颗卫星的伪距为ρBi=ri-δtu-υρ。其中，δtu为等效距离误差，vρ为量测噪声，其主要和伪距残差有关，常见的如多径误差等[2]。

可通过如下表达式描述距离差量测方程：

(14)

综合式 (6)～(14)，可以得到最终的伪距量测方程：

Zρ(t)=Hρ(t)X(t)+Vρ(t)

(15)

其中:

(16)

SINS位置与第i颗卫星之间的距离变化率在(x，y，z)点线性化之后得到：

(17)

(18)

由于SINS输出的导航参数是真实值与误差值之和，所以有：

(19)

由此，SINS导航解算的距离变化率可表示为：

(20)

BDS接收机测量输出的伪距率为：

(21)

综合式(20)和(21)，紧组合导航系统伪距率量测方程如下：

(22)

由此，伪距率量测方程可表示为：

(23)

其中:

由以上各式得到伪距、伪距率组合方式测量方程为[18]：

(24)

2 多假设解分离的完好性监视

完好性主要表示系统在无法完成预定工作情况下及时准确的发送有效告警的能力[5,11-13]，对这种系统而言，需要在规定期限内提供超限警报信息给用户[5,11-14]。可通过三个指标描述完好性，也就是完好性风险，保护限、告警时间，以下进行具体描述[5,11-15]。

保护限(protection limit，PL)可划分为水平(horizontal protection limit，HPL)和垂直(vertical protection limit，VPL)两个方向的保护限，可通过其反映出相应虚警和漏检概率的径向位置误差最小值[11,12,15]。后续以水平保护限为例分析多解分离的完好性监视方法。根据PBN运行要求及特点，不同的飞行阶段对应不同的告警限值(alarm limit，AL)。当PL超出指定飞行阶段的AL时，系统应给出告警。

告警时间(time to alarm，TTA)具体表示从系统出现故障到发出告警的时间差，告警时间为Δt=t2-t1。根据安全性要求，不同飞行阶段所对应得最大允许告警时间tmax不同，若Δt≤tmax表示系统完好性能及时告警；反之，为漏警。

完好性风险含义为系统误差超过告警限制但没有发出报警的概率[4,11]。若计算结果表明相应位置误差超过设定值情况下，需要在告警期限内发出报警信息；而若没有发出报警，则可判断存此类风险。也即：

PIntegrity_Risk=

(25)

2.1 基于多解分离的扩展卡尔曼滤波结构

如图2反映出这种滤波器结构，分析可知其中具体包括主滤波器F00、N个子滤波器和N-1个次滤波器。而对应的主滤波器的量测信息主要为全部N颗BDS可见星的测量结果；其中子滤波器中含有其他BDS可见星的测量信息；次滤波器中的观察信息和前者的属性相同。在运行过程中接收到的卫星信息中有故障情况下，必然有一个子滤波器的状态解和主滤波器的存在偏离。这样在主滤波器和一个或者多个子滤波器的分离解大于设定值情况下，系统会发出报警信息，可根据相应的子与次滤波器的分离解来实现隔离目的[3,13,19]。

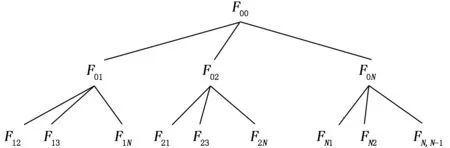
图2 多解分离滤波器结构

2.2 基于多解分离的完好性监视

可通过如下表达式描述k时刻主滤波器和某子滤波器估计解的分离向量：

(26)

其协方差为：

(27)

建立起各子滤波器统计量：

(28)

在已知误警率PFA条件下，可确定出和各统计量d0n相关的判断阈值T0n为：

(29)

在隔离BDS观测数据过程中，可应用N个子滤波器相关的统计量，相应的判据表示为：

1)无故障H0：所有子滤波器对应的检验统计量均有d0n≤T0n；

2)有故障H1：至少存在一个子滤波器对应的检验统计量d0n>T0n[3,13,19]。

图4 故障发生时各子滤波器的完好性监视输出

对其中子和次级滤波器的分离解进行分析就可塑实现故障隔离的目的。相应的算法和故障检测的基本上一致。可基于其解分离向量确定出统计量dnm和对应的阈值Tnm。检测并验证第r颗卫星故障的判据为：对全部n≠r，有一个或者多个次滤波器相关的统计量高于阈值[3,13,19]。

每个子滤波器的水平保护限用下式计算：

HPLn=T0n+a0n

(30)

其中:T0n表示该子滤波器对应的判决门限；a0n表示该子滤波器F0n本身的水平位置误差门限[11,23,41,50]。记λP0n为水平位置误差向量协方差阵P0n的最大特征值[3,11,13,19]，根据漏检率PMD要求，可得：

(31)

进而得到多解分离的水平保护限为[11,,23,41,50]：

HPL=max(HPLn)=max(T0n+a0n)

(32)

2.3 BDS/SINS紧组合完好性监视仿真与分析

在以上分析基础上，接着模拟仿真这种接收机的卫星观测数据误差情况。在进行导航解算过程中，可在各时空点选取满足要求的GDOP值最大的6颗可见星，且将故障信息加在检测难度最大的卫星上。

故障参数设置如下：对应的观测卫星GEO3在11 s时出现斜坡率为0.63 m/s的斜坡故障，持续时间为129 s。飞行阶段设定为非精密进近阶段，漏警、误警概率要求、告警时限遵循非精密进近阶段的要求，如图3所示。

图3 测试阶段多解分离算法计算的保护限

在出现故障情况下，如图4(a，b，c，d，e，f)显示了各卡尔曼滤波器的输出结果，分析此图可知11 s时在GEO3的观测值出现了0.63 m/s的斜坡误差，运行过程中，子滤波器F03在13 s时检验到观测值超出设定值，而发出报警提示。在18 s时各子滤波器位置解的水平定位误差高出设定值，据此可判断出：在出现卫星故障情况下，多解分离法可控制定位误差低于设定值，或者发送报警提示，而相应的告警时间也在合理限度内，满足要求。

为了对这种算法的虚警率和漏检率进行验证，判断是否在许可范围内，而开展了蒙特卡洛试验。在此实验过程中选取8 000个时空点来模拟仿真，相应的故障设置情况为，每隔120个时空点随机情况下加一次故障，对所得结果进行整理，如图5所示，测试数据的仿真情况见表1。

表1 statistical result data of Monte Carlo simulation

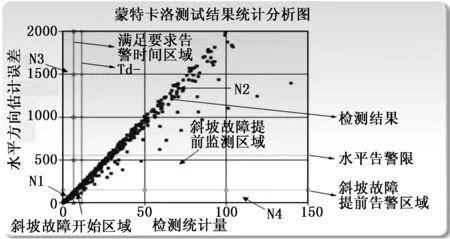
图5 蒙特卡罗测试结果统计分析图

分析以上结果可知，虚警率为1.25×10-4，而漏检率为0，虚警率高的原因为多解分离算法结果容易受到慢变的斜坡故影响。

3 结束语

本文分析了SINS和BDS导航的误差特点，搭建了扩展卡尔曼滤波的BDS/SINS深组合系统，利用多假设解分离算法对BDS/SINS紧组合导航系统的完好性监视算法进行了完善，选择最大GDOP的6颗卫星组合，通过在最难检测的卫星上人为加入误差信号，进行故障卫星的检测与隔离，并计算水平保护限，仿真结果表明该方法能够有效实现故障卫星的检测与隔离，满足导航系统完好性算法的要求。论文选择了最差的情况，只考虑单颗卫星故障。当多颗卫星故障时，可以用同样的方法解决，但所需的卡尔曼滤波器的数量会急剧增加，影响处理速度。