宏弯型光纤位移传感器的分析与设计*
左路路,金 韬*,何 流,刘伟明,朱 翔,汪启杭
(1.浙江大学信息与电子工程学院,杭州 310027;2.浙江中技建设工程检测有限公司,杭州 310012)
裂缝监测是危房评估领域的一个重要指标[1],位移传感器可以将裂缝信息转化为电信号进行处理,实现对裂缝的实时监控,其发展可分为经典电磁位移传感器阶段和半导体位移传感器阶段[2]。前者因利用电磁学理论直接在电域进行信号采集,存在着电磁学的固有缺点[3]。而作为后者的光纤类位移传感器利用光束在光域进行信号采集,摆脱了电域信号采集的缺点,同时拥有诸如灵敏度高、耐腐蚀、质量轻、抗电磁干扰能力强等优点[4-5]。
近年来,光纤位移传感器被越来越多地应用到建筑裂缝监测中[6-9]。根据其作用机理,可分为本征型和非本征型两类[10]。本征型光纤位移传感器又可分为微弯型和宏弯型两类。其中微弯型光纤位移传感器利用光纤轴向上的微弯效应感知位移变化,可监测的裂缝位移量程较小,仅为2 mm左右[11-13],且光纤输出功率随裂缝间距变化的线性度较差[14-15];而宏弯型光纤位移传感器利用光纤宏弯损耗来感知位移变化,测量量程较大,且结构简单,便于应用。
位移传感器也被称为线性传感器[10],线性度水平和测量量程是衡量其性能的重要指标。为了提高这两项指标,产生了不同结构的宏弯型光纤位移传感器。常见简单的宏弯型光纤位移传感器[16-19]结构如图1所示,光纤分为固定和悬空部分,其中固定部分的光纤与裂缝两侧的基体紧密结合,不随裂缝的变化发生结构形状的变化;悬空部分的光纤处于裂缝之间。当裂缝发生变化时,悬空部分的光纤弯曲结构发生变化,导致其光损耗的变化。通过测量光纤弯曲产生的光损耗可间接获悉裂缝宽度的变化。本文提出了一种新的分析该宏弯型光纤位移传感器的数学模型,通过对光纤损耗的理论仿真和实验数据的分析,设计出了一种线性度好、测量量程大、结构简单的宏弯型光纤位移传感器。

图1 宏弯型光纤位移传感器
1 光纤传输损耗的理论分析
从材料分类,光纤主要有聚合物光纤和石英光纤两类。聚合物光纤的光衰减较大,不适合远距离传输[20],然而在光纤位移传感中,主要利用光纤宏弯产生的光损耗作为特征值进行裂缝测量,一般不需要远距离传输光信号,而聚合物光纤较大的弯曲衰减特性对于传感应用尤为合适。另外,聚合物光纤的数值孔径较大,使得其与光源的耦合较为简单[21],且柔韧性较好,不易折断[22],安装固定较为方便[23]。综合考虑,在裂缝传感中,聚合物光纤有着石英光纤不可比拟的优点。因此,选用聚合物光纤作为裂缝传感的敏感介质。
根据D.Marcuse的光纤宏弯损耗理论[24-25],经化简整理后的聚合物光纤宏弯损耗系数2αB为:
(1)
式中:R为光纤宏弯曲率半径,φ1和φ2均是与传输光波长和光纤参数有关的常数[26]。
对于一段长为L、曲率半径恒为R的光纤,设其输入端光功率为Pin(单位:mW),输出端光功率为Pout(单位:mW)。根据定义可知:Pout/Pin=e-2αBL,则宏弯损耗DB(单位:dB)为:
=-10lge-2αBL=10(lg e)×2αBL
(2)
2 仿真模型的建立与分析
2.1 宏弯结构模型的建立
通过对图1所示的光纤宏弯结构进行数字图像处理[27],可以得到沿光纤中心轴的曲率半径分布,如图2所示。
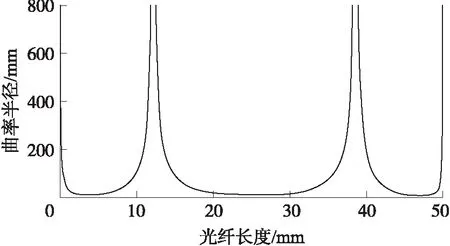
图2 宏弯型光纤曲率半径分布
如果要对该光纤宏弯结构进行光损耗理论计算,需要获知沿光纤每一点的曲率半径。如果要计算随裂缝变化的光损耗,则更需要获取不同裂缝情况下沿光纤每一点的曲率半径。显然,这是不现实的,因此需要对该光纤宏弯结构进行建模以便于光损耗的理论计算。
由光纤弯曲损耗公式可知,曲率半径越小,光纤弯曲损耗系数越大,所以在图1的光纤宏弯结构中,光损耗主要是由裂缝中悬空部分的两侧和中间的光纤弯曲结构造成的。因此,可以将光纤宏弯结构分解为两侧的圆弧、中间的圆弧和连接它们的直线三个部分,可认为整体光损耗基本由两侧和中间的圆弧部分的光纤光损耗累加产生。显然,左右两侧和中间的圆弧中任何一部分的光损耗与裂缝位移之间都没有很好的线性关系,最终输出的整体光损耗与裂缝位移之间也没有很好的线性关系。
然而,图1中固定部分的光纤所在直线的斜率会影响裂缝中悬空部分的两侧圆弧和中间圆弧的弯曲程度以及在整体光损耗中的占比。因此,通过不断调整固定部分的光纤所在直线的斜率,可以寻找到使得整体光损耗与裂缝位移之间线性关系达到最好的结构。根据固定部分的光纤所在直线斜率的不同,进行以下不同情况的分析。
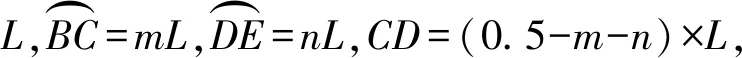
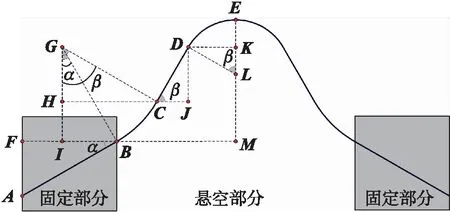
图3 α>0且HC>BI时的宏弯型光纤结构
第一种情况如图3所示,裂缝间距较小时,HC>BI,经推导可得裂缝间距X为:
(3)
式中:β为连接侧边圆弧和中间圆弧的直线与水平线的夹角。
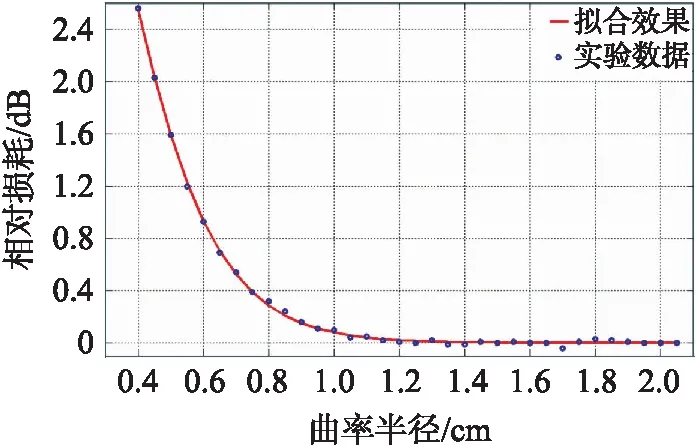
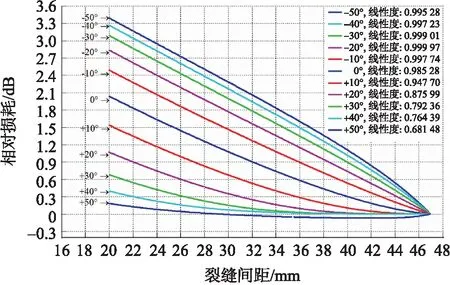
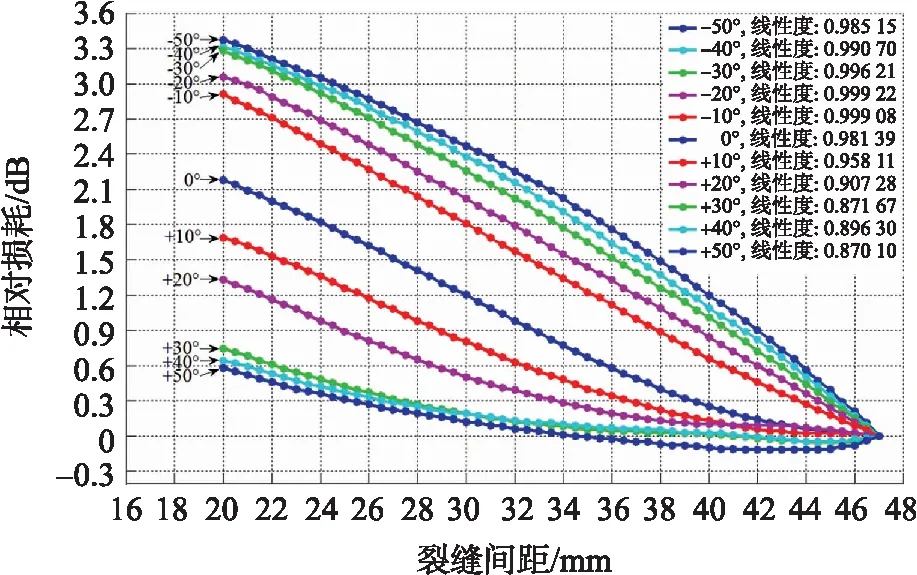
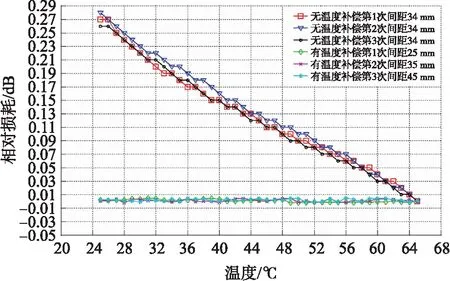
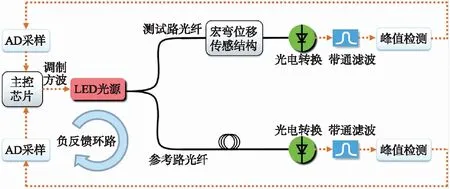
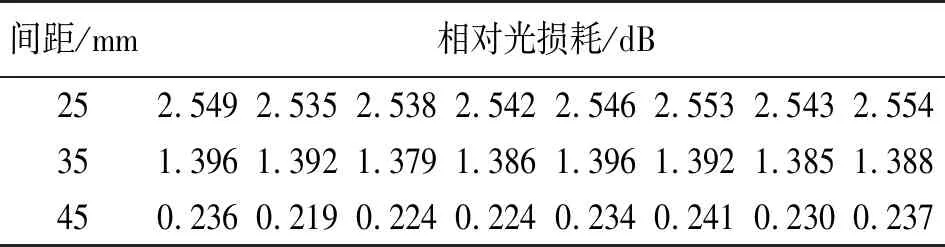
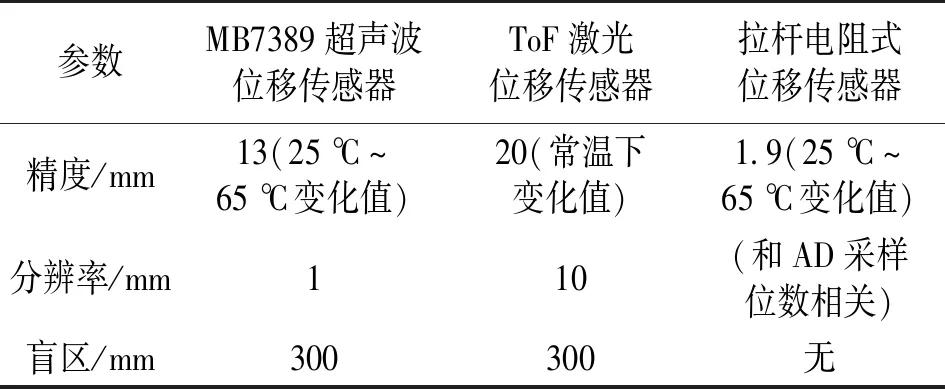
第二种情况如图4所示,裂缝间距较大时,HC 图4 α>0且HC 其次,如图5所示,固定部分AB线段的光纤所在直线的斜率为负,规定其与水平线的夹角α为负值,图中用-α表示实际非负角度值。经推导,裂缝间距同样也可用式(3)表示。 图5 α<0时的宏弯型光纤结构 综上所述,三种情况下的裂缝间距均可由式(3)描述,式(3)中只有β为变量,其余参数均为常量,因此裂缝间距只与变量β相关,这为计算仿真带来了方便。 根据光纤宏弯损耗式(2)和宏弯结构模型,可以得到光通过裂缝间光纤后产生的总的光损耗DB为: (4) 式中:φ1、φ2是可以通过实验测定的常量。由式(1)和式(2)可知,长度为L、曲率半径恒为R的光纤产生的弯曲损耗(单位:dB)为: (5) 为了测试方便并提高准确度,将光纤以螺旋方式紧密缠绕在圆柱上n圈,则光纤环长度为: (6) 式中:r为光纤包层半径,联立式(5)和式(6)可得: (7) 实验中,光纤包层半径r为0.05 cm,光纤缠绕圈数n取5,光纤环半径R以0.5 mm逐次变化,如图6所示。采集不同光纤环半径下的光损耗值,根据式(7)对采集的数据点进行非线性拟合,如图7所示,得到φ1值为1.85,φ2值为-8.05。 图6 实现不同半径光纤环的实验装置 图7 φ1、φ2常量的拟合曲线 L是实验中固定端之间光纤总长度,根据常见墙体裂缝变化范围以及光纤形态变化情况,取值为50 mm,m、n是仿真分析过程中设定的光纤两端弯曲部分和中间部分的一半所占总光纤长度的比例,通过反复调整和校验,当设定m为3/50、n为7/50时,仿真分析的结果与实验结果最为匹配。α是固定部分的光纤所在直线的斜率,从-50°~50°以10°为间隔依次进行了仿真分析和实验测试。 综上所述,式(3)和式(4)中只有β为变量,其余参数φ1、φ2、L、m、n、α均为常量,因此光损耗DB只与变量β相关。联立式(3)和式(4),二式的自变量均为β,因变量分别为裂缝间距X和光纤损耗DB,通过MATLAB等软件绘制出曲线DB=f(X),即光纤损耗随裂缝的变化情况。改变常量α,可计算在不同初始夹角α下光纤损耗DB随裂缝间距X的变化情况。 固定端之间光纤总长度为50 mm,当固定端间距拉伸至50 mm时,如果固定端的光纤所在直线的斜率不为0,则在固定端处光纤会发生塑性形变,将对光纤造成不可逆的损伤。为了对比固定端光纤不同直线斜率下的多种情况,经过多次实验测试,设定固定端间距最大值为47 mm。当固定端间距过小时,光纤会因材质特性发生三维方向的旋转,不能使其保持在同一平面内,导致光损耗来源的分析变得尤为复杂,为了避免这种情况的发生,通过不断的测试调整,设定固定端间距最小值为20 mm。 以裂缝间距为47 mm时的光纤输出光功率为基准,记此时的光损耗为0 dB。测试不同初始夹角α下光损耗与裂缝间距的关系,结果如图8所示。当夹角α为-20°时,曲线的线性度最好(定义R2为衡量曲线线性度水平的参数,其中R2=回归平方和/总平方和,值越接近1表示曲线线性度越好),裂缝变化范围20 mm~47 mm。 图8 不同夹角α下的宏弯损耗与裂缝间距的关系 图9 整体实验结构 实验采用波长650 nm的LED作为光源,纤芯直径0.5 mm、包层直径1 mm的聚合物多模光纤作为导光光纤,裂缝之间光纤长度L为50 mm。在恒温环境下,利用位移平台模拟裂缝变化,利用光功率计检测光纤输出光功率的大小,整体结构如图9所示。 输入输出引导光纤与水平线夹角在-50°~50°之间以10°为间隔变化,测量并记录裂缝间距从20 mm~47 mm变化过程中光纤的输出光功率。以裂缝间距47 mm时的光纤输出光功率为基准,计算其余情况下的相对光损耗,结果如图10所示。由图10可见,当夹角α为-20°时,光功率损耗和裂缝间距之间的线性度最好,和仿真结果一致。理论仿真和实验测试结果的吻合验证了构建的宏弯结构模型的正确性。 图10 不同夹角α下实验测量的宏弯损耗与裂缝间距的关系 聚合物光纤的材料特性决定了在位移传感中光损耗易受到环境温度的影响,当采取无温度补偿方案时(设置输入输出引导光纤与水平线夹角α为-20°,裂缝间距为34 mm),将其中模拟裂缝位移结构的装置放置到恒温箱中,测量温度范围为25 ℃~65 ℃,温度间隔为1 ℃。测量过程中裂缝位移不变,以65 ℃时的光纤输出光功率为基准,记此时的光损耗为 0 dB。重复三次实验观察温度对光损耗的影响,测量结果如图11所示。在该温度范围内,相对光损耗变化了约0.27 dB,因此温度的确会对测量结果产生较大的影响。 图11 补偿前后光损耗受到温度的影响情况 实际应用时采取了利用反馈调节方式实现的温度补偿方案。整体方案如图12所示,光源发出的光信号一分为二输出到两条相同属性的聚合物光纤,其中一条光纤作为测试路,用于检测裂缝位移信息,另外一条光纤作为参考路,用于检测温度等因素导致的光纤传输损耗变化。测试路和参考路的光信号经过相同的光电转换、放大采集等处理后传输到控制芯片,由控制芯片根据参考路信号对光源幅度进行反馈调节。利用该补偿机制对多个间隙进行测试,结果如图11所示,波动峰峰值为0.007 dB,基本消除了温度的影响。 图12 反馈补偿方案整体框图 灵敏度即宏弯损耗与裂缝间距之间关系曲线的斜率。当初始夹角为-20°时线性度最好,在图8的仿真分析中,对应拟合直线的斜率为-0.104,故其理论灵敏度为-0.104 dB/mm;同理在图10的实验测试中,对应拟合直线的斜率为-0.116,故其实验灵敏度为-0.116 dB/mm。 测量精度即间距测量的最大测量误差。在反馈补偿方案下,输出信号波动的峰峰值最大为0.007 dB,因此,理论精度为:(0.007/0.104)mm ≈ 0.067 mm,实验精度为:(0.007/0.116)mm ≈ 0.060 mm。 测量分辨率与AD采样位数相关。在反馈补偿方案下,使用16位AD芯片进行数据采集,输入电压信号范围为0~5 000 mV,因此1位对应电压值为0.076 mV。光损耗最小(即间距为47 mm)时设置为满量程5 000 mV,在初始夹角为-20°的仿真分析中(见图8),量程范围内光损耗变化了2.841 dB,因此在间距为20 mm时输入电压信号为2 599.381 mV,此时分辨率最差,其值为1.221 μm;同理在初始夹角为-20°的实验测试中(见图10),量程范围内光损耗变化了3.124 dB,因此在间距为20 mm时输入电压信号为2 435.398 mV,此时分辨率最差,其值为1.168 μm。 为了测试稳定性和重复性,在初始夹角为-20°(即线性度最好)的情况下,选取了固定端间距分别为25 mm、35 mm和45 mm的三种情况,每间隔1 h对三种情况进行多次实验测试,结果如表1所示。 由表1可见,三种间距下的相对光损耗平均值分别约为2.545 dB、1.389 dB、0.231 dB,计算可得测量间距平均值分别约为25.060 mm、35.024 mm、45.012 mm,对应的均方差分别为0.059 mm、0.051 mm、0.066 mm。 表1 稳定性和重复性测试 此外,我们对常见的超声波、激光和拉杆电阻式三种类别的位移传感器的性能进行了实验测试,测试对比结果如表2所示。测试数据表明,本文设计的宏弯型光纤位移传感器的精度、分辨率等参数均优于这三种位移传感器,同时具有很强的抗温度干扰能力。 表2 不同类别位移传感器性能测试 本文提出了一种用于分析宏弯型光纤位移传感器光传输损耗的数学模型,通过理论仿真优化和实验验证,设计和制作了一种高线性度、大测量量程且结构简单的宏弯光纤位移传感器。采用反馈补偿机制可显著提高传感器的长期稳定性和重复性,其测量精度、分辨率等性能参数均优于超声波、激光和拉杆电阻式等传统的位移传感器,其理论最优线性度达到0.999 97,实测达到0.999 22,最大测量量程27 mm。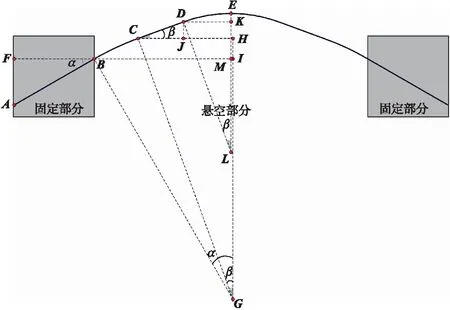
2.2 传感器结构的仿真分析


3 传感器的实验测试
4 传感器的性能分析
5 结论

