抓住关键信息 寻找解题方法

重庆市南川道南中学(408400) 汪仁友

近几年高考数学试题中出现了一种新题型：数学文化试题.该类试题的特点是文字较多,学生在考试时常常读题需要花较多时间.其实我们在做该类试题时,不要在过多的数学文化介绍上花太多时间,只要抓住题目中的关键信息,即可获得解题方法.下面以2019年全国卷ⅠⅠ理科试题为例说明之.

例1(2019年高考全国卷ⅠⅠ理科第4题)2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日L2点的轨道运行.L2点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,L2点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程：由于α的值很小,因此在近似计算中则r的近似值为( )

思路1抓住已知等式及关键信息,从构造α入手.

解法1由

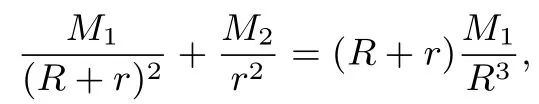
得

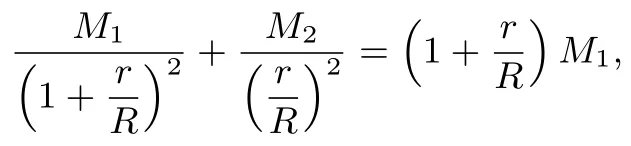
则

即

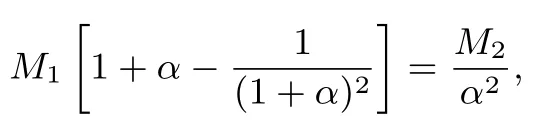
所以

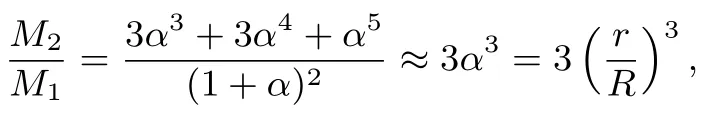
思路2抓住已知等式及r=αR关键信息,从消去r入手.

解法2把r=αR代入已知等式,得

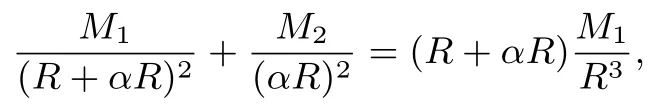
所以

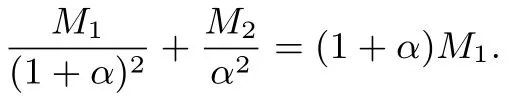
以下同解法1.

思路3抓住已知等式及关键信息,从消去R入手.

解法3把代入已知等式,得

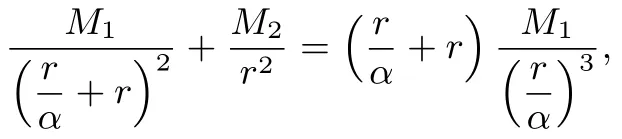
则

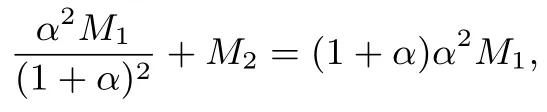
即

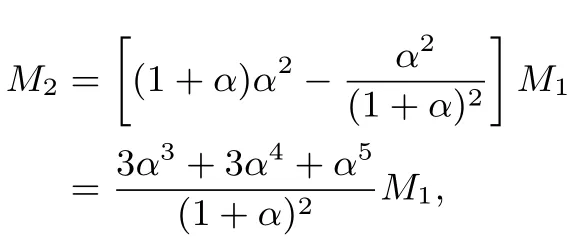
所以

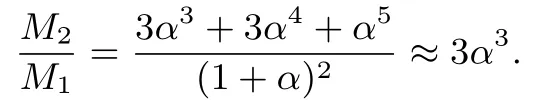
以下从略.

思路4抓住题目答案中的关键信息.因为四个答案中均含,所以我们可以从已知等式计算入手.

解法4由已知等式得

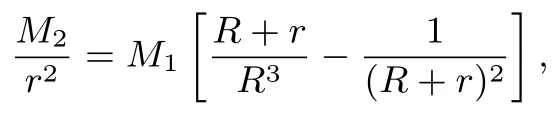
所以

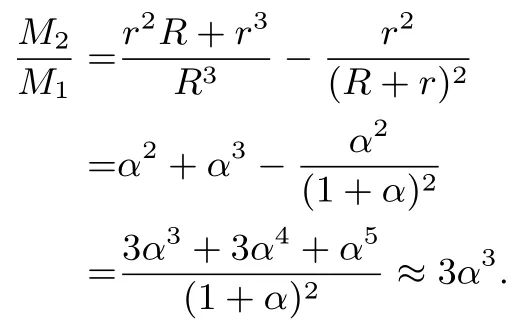
以下从略.

评注本题以“嫦娥四号”航天探测为背景,以方程的近似解为平台,注重数学文化,体现育人导向的同时考查了考生数据处理、数学运算核心素养及换元思想、化归与转化思想的应用.但学生在考试时,觉得读题比较费力,还需要较多的时间.其实该题即是前面的文字部分读不懂,只要我们抓住后面的等式,充分利用α与R和r的关系等关键信息,就可以获取解题方法.

图1

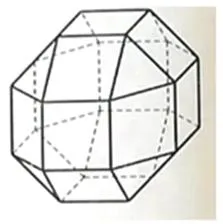
图2

例2(2019年高考全国卷ⅠⅠ理科第16题)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有_____个面,其棱长为____.(本题第一空2分,第二空3分.)

解析第一空只要抓住“图2”图形这个关键信息,即可得出答案为26.第二空抓住“半正多面体”是由正多边形围成的多面体,即它的棱长均相等,以及顶点都在同一个单位正方体的表面上这个关键信息,将它放在单位正方体中,即可得出答案为

评注本题以数学文化为背景,以半正多面体为载体,考查了考生空间想象能力和运算求解能力,同时也考查了直观想象、逻辑推理、数学运算等核心素养.只要我们抓住“半正多面体”的定义及空间图形关键信息,就可以获取解题方法.