认清特性 巧解极坐标与参数方程问题

云浮市郁南县西江中学(527100) 周坤荣

“极坐标与参数方程”是近三年全国卷高考数学题“二选一”的第一题,分值为10分.从选择性来看,近三年每年都有百分之九十左右的广东考生选做这题,足见考生和教师对这题的青睐!从平均分来看,18年这道题广东理科平均分为5.23分,文科为3.87分,2019年的文理平均分都有下降的趋势!大部份学生只能做这道题的第一问,在第二问方程的应用上很难取得突破!事实上,此题在解答题中属于中易难度题,属于必得分数题,考生只要充分理清三种方程各自的特性,准确选择方程的形式,定能取得“极坐标与参数方程”应用的突破!

笔者曾对本校高三级三百多名文科生做过关于“极坐标与参数方程”这道选做题的问卷调查,调查显示68%高中文科生都把极坐标系中的问题转化成直角坐标系中的问题来解决,学生对极坐标系的方程和图形的关系不熟悉,对参数方程中参数的几何意义没理解透彻,对直线参数方程的标准形式理解不完整,怕出错不得不选择直角坐标系进行复杂的代数运算.认清三种方程各自的特性是突破这道题的前题.

1.熟悉的直角坐标方程

直角坐标方程是学生最熟悉的方程,学生易跟据曲线的直角坐标方程看出曲线的类别,作出图象,得出基本特征且便于学生进行相计算和解有关方程组.对于求曲线间的交点,定点到线的距离和处理直线与圆的位置关系等较直观的问题,可选用直角坐标方程去解决!

例1(2013年高考新课标Ⅰ卷)已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.

(1)把C1的参数方程化为极坐标方程;

(2)求C1与C2交点的极坐标(ρ≥0,0≤θ＜2π).

分析(1)略;(2)求两个圆交点的极坐标,问题的关键在于解方程组,若选择用极坐标表示曲线的方程,解极坐标方程组学生明显较为生梳,解方程组过程出现的三角函数化简与变换对学生也是不小的挑战.若曲线的方程用直角坐标方程表标,所解方程组学生相对是熟悉的,学生只要先求出两圆交点的直角坐标再化成极坐标表示即可!

解析(1)将消去参数t,化为普通方程(x-4)2+(y-5)2=25.即C1:x2+y2-8x-10y+16=0.将代入x2+y2-8x-10y+16=0得ρ2-8ρcosθ-10ρsinθ+16=0,所以C1的极坐标方程为ρ2-8ρcosθ-10ρsinθ+16=0.

(2)C2的普通方程为x2+y2-2y=0.由

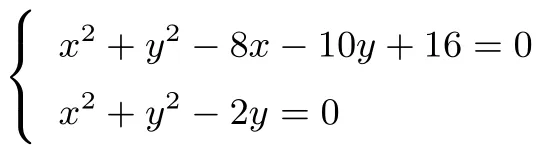
例2(2018年高考全国Ⅰ卷理科)在直角坐标系xOy中,曲线C1的方程为y=k|x|+2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2+2ρcosθ=0.

(1)求C2的直角坐标方程;

(2)若C1与C2有且仅有三个公共点,求C1的方程.

分析(1)略;(2)考查圆与动直线的位置关系,在直角坐标系中,有关直线与圆的图象,性质及相互间的位置关系学生都比较熟悉,所以本题第二问曲线的方程选用直角坐标方程表示,方便学生作图,进而理清直线与圆的位置关系.

解析(1)由x=ρcosθ,y=ρsinθ得C2的直角坐标方程为(x+1)2+y2=4.

(2)由(1)知C2是圆心为A(-1,0),半径为2的圆.由题设知,C1是过点B(0,2)且关于y轴对称的两条射线.记y轴右边的射线为l1,y轴左边的射线为l2.由于B在圆C2的外面,故C1与C2有且仅有三个公共点等价于l1与C2只有一个公共点且l2与C2有两个公共点,或l2与C2只有一个公共点且l1与C2有两个公共点.

当l1与C2只有一个公共点时,A到l1所在直线的距离为2,所以故k=或k=0.检验,当k=0时,l1与C2没有公共点;当k=时,l1与C2只有一个公共点,l2与C2有两个公共点.

当l2与C2只有一个公共点时,A到l2所在直线的距离为2,所以故k=0或经检验,当k=0时,l1与C2没有公共点;当时,l2与C2没有公共点.综上,所求C1的方程为

2.灵动的参数方程

曲线的参数方程选择的参数不同,可有不同的形式.参数方程的参数一般有特殊的几何意义,如果对参数的几何意义能理解透彻,处理起某些问题能起到事半功倍的效果!参数方程能把曲线上的点用一个变量(参数)表达出来,这比用直角坐标少了一个变量,便于后面的化简、求值和处理有关取值范围的问题.对于处理直线与曲线相交的长度或与曲线上一个动点有关的问题,曲线的方程可选用参数方程,把曲线上的动点用参数表示,这样可以把目标问题转化成于参数θ(或t等)的目标函数!

例3(2019年高考全国Ⅰ卷)在直角坐标系中,曲线C的参数方程为(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为2ρcosθ++11=0.

(1)求C和l直角坐标方程;

(2)求C上的点到l距离的最小值.

分析(1)利用代入消元法,可求得C的直角坐标方程;(2)利用参数方程表示出C上点的坐标,根据点到直线距离公式可将所求距离表示为三角函数的形式,从而根据三角函数的范围可求得最值.

解析(1)由x=得：t2=,又y2=,所以

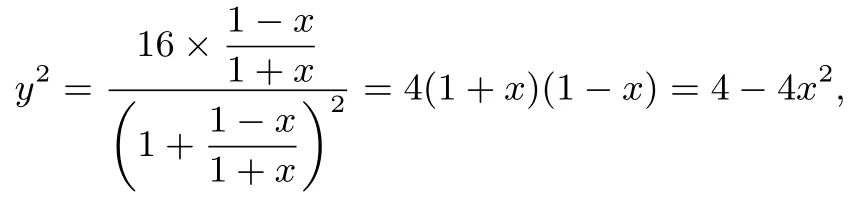
整理得C的直角坐标方程为：又x=ρcosθ,y=ρsinθ,所以l的直角坐标方程为：11=0.

(2)设C上点的坐标为：(cosθ,2sinθ),则C上的点到直线l的距离

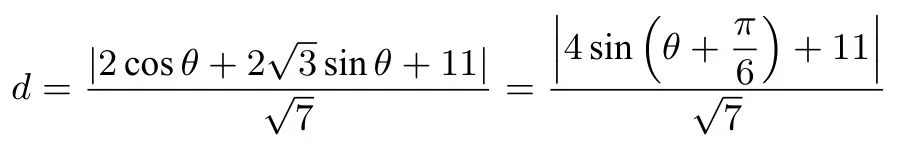
例4(2016年高考全国ⅠⅠⅠ卷)在直线坐标系xOy中,曲线C1的参数方程为(α为参数).以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为

(Ⅰ)写出C1的普通方程和C2的直角坐标方程;

(ⅠⅠ)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.

分析(1)略;(2)这是关于两线上两动点距离最值问题,通过作图分析知当直线的平行线与椭圆相切时,|PQ|取得最值,难点是学生是否会把问题转化为相切;动点Q在直上,|PQ|的最小值等价于P到直线x+y-4=0距离的最小值,可把两个动点的问题转化成一动点的问题,利用参数表示出P的坐标,再用点到线的距离公式把目标问题转化为关于参数的三角表达式,最后用三角函数相关知识求出最值即可!

解析(Ⅰ)C1的普通方程为的直角坐标方程为x+y-4=0.

(ⅠⅠ))由题意,可设点P的直角坐标为因为C2是直线,所以|PQ|的最小值,即为P到C2的距离d(α)的最小值,

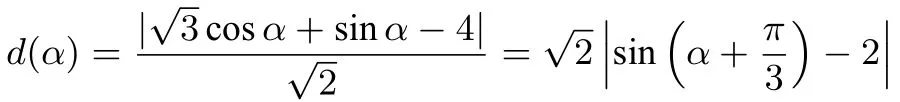
3.最有几何性的极坐标方程

极坐标系是坐标系的一类,相对于直角坐标系学生会感到有些生梳,但对于有特殊性的几何图形,极坐标系更易表达出相关点、边间的特殊关系.

对于过极点的直线,垂直等特殊的图形及出现多个动点的问题,曲线的方程可选用极坐标方程来表示.有多个动点的问题,要注意找出动点间极角的关系,尽可能用一个变量表示出所有动点的极角,最后把问题转化成关于极角的目标函数!

例6(2018年佛山一模)在直角坐标系xOy中,直线l的参数方程为

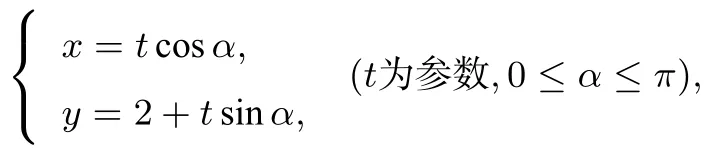
曲线C的参数方程为

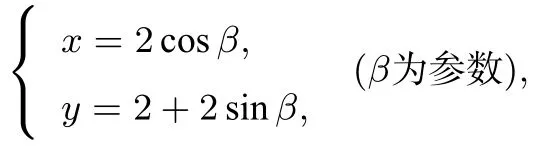
以坐标原点O为极点,x轴正半轴为极轴建立极坐标系.

(1)求曲线C的极坐标方程;

(2)设C与l交于M,N两点(异于原点),求|OM|+|ON|的最大值.

分析(1)略;(2)作出相关图形易知,直线l经过圆C的圆心,则△MON为直角三角形,若用极坐标表示,则M,N两点的极角只需引入一个变量即可,而|OM|,|ON|刚好为M,N两点的极径,根据极坐标方程极径可以用关于极角的三角函数表达,最后对三角函数式进行化简整理即可求得最值!

解析(1)因为曲线C的参数方程为(β为参数),所以消去参数β,得曲线C的普通方程为x2+(y-2)2=4.化简得x2+y2=4y,则ρ2=4ρsinθ,所以曲线C的极坐标方程为ρ=4sinθ.

(2)因为直线l的参数方程为

所以由直线l的参数方程可知,直线l必过点(0,2),也就是圆C的圆心,则∠MON=,不妨设M(ρ1,θ),N(ρ2,θ+),其中则

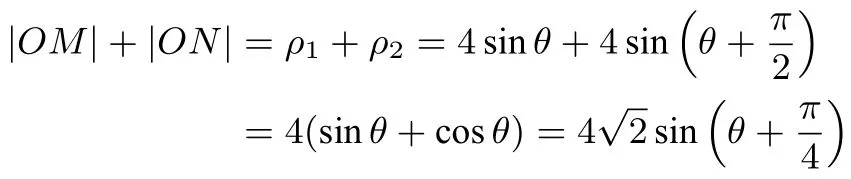
教师在“坐标系与参数方程”模块的解题教学中,要结合相关图形,理清三种曲线方程的本质与特性,对题型进行分析、比较和归类.只要善于进行系统总结和综合分析,就能发现和掌握知识的内在规律,从而举一反三,触类旁通,收到“一览众山小”的效果!