立体引学,活力课堂

广东省高州中学(525200) 李文聪

“立体引学”是教师引导学生的自主合作探究学习.概念教学是基础知识和基本技能教学的核心,正确理解数学概念是学好数学的基础,是数学教学的重要环节.本文结合数学概念课立体引学教学实践,从“明确学习目标,找准引学方向;结合学生实际,找准引学起点;运用学习心理,找对引学策略”三方面打造活力课堂.

一、明确学习目标,找准“引学”方向

数学新概念的形成是由特殊到一般,由具体到抽象的过程.对于那些初次接触或较难理解的数学概念,可以采用概念的形成方式进行学习.其教学过程为：提供概念例证→抽象出本质属性、形成初步概念→概念的深化→概念的运用[1].

幂函数是基本初等函数之一,是在学生系统学习了函数、指数函数、对数函数的概念和性质之后,掌握根式和有理数指数幂的基础上学习的一种特殊函数.学习幂函数是对函数概念和性质的进一步应用.我们先让学生列出下列问题中的函数式：

问题1如果张红购买了每千克1元的蔬菜w千克,那么她需要付的钱数p=w元,这里p是w的函数.

问题2如果正方形的边长为a,那么正方形的面积S=a2,这里S是a的函数.

问题3如果正方体的边长为a,那么正方体的体积V=a3,这里V是a的函数.

问题4如果正方形场地的面积为S,那么正方形的边长,这里a是S的函数.

问题5如果某人ts内骑车行进了1km,那么他骑车的平均速度v=t-1hm/s,这里v是t的函数[2].

引导学生观察归纳出这五个函数的共同形式特征：(1)都是以底数为自变量,以幂的值为函数值;(2)幂指数是常数;(3)只有一项,且系数为1.综合以上三个特点,得出以上函数都形如y=xa的形式,a是常数,x为自变量.通过实例归纳,形成幂函数的概念：一般地,形如y=xα的函数称为幂函数,其中a是常数,x为自变量.这样通过对实例的归纳分析,学生认识了幂函数的特点,再给出幂函数定义,学生易于理解,易于撑握.

二、结合学生实际,找准“引学”起点

教学中,教师必须了解学生原有的数学认知结构,知识基础及智力、能力、个性心理特征等,才能为学生选择提供合适的数学材料,对学生缺乏的进行补充,使那些模糊和欠稳定的部分变得清晰和稳定,使新的数学知识和学生原有的知识联系起来.

以下是笔者的教学片段实录：

一枚炮弹发射后,经过26s落到地面击中目标,炮弹的射高为845m,且炮弹距地面的高度h(单位：m)随时间(单位：s)变化的规律是h=130t-5t2,那么炮弹距离地面的高度h是时间t的函数吗？[3]

生1：对于任一个给定的时间t,都有唯一确定的高度h与之对应,因此h是t的函数,其解析式是h=130t-5t2.

师：好！很有道理.你能说出t=1s,10s,100s时对应的高度h吗？

生3：t=1s时,h=125m,t=10s时,h=800m,t=100s时,h=3700m..师：请想一想,学生3回答正确吗？

生4：由于炮弹在26s时已经落到地面爆炸了,因此在t=100s时没有高度跟它对应了.

师：很好！细节决定成败.学生3的计算正确,但未能联系实际,学生4则关注了实际情况.请问任给一个时间t,都有唯一确定的高度h与之对应吗？

生5：对于0s：26s之间的每一个时间t,都有唯一确定的高h=130t-5t2与它相对应.

师：0s：26s是我们生活中的语言,其实我们可以用集合表示这个范围,你能说出这个集合吗？

生6：A={t|0≤t≤26}.

师：对！那么高度h也能用集合表示吗？

生7：B={h|0≤h≤845}.

师：非常好！我们用集合的语言重新表述这个实例中的对应关系,谁来说一说.

生8：对于集合A中的每一个时间t,集合B中都有唯一的数值h与之对应.

师：精辟！本例中用集合的语言描述了炮弹距离地面的高度h是时间t的函数关系.

上例以问题为主线,采用一系列的设问、引导、启发、发现,让学生归纳概括出函数概念,突破本节课的难点,符合学生的认知规律,学生容易理解.

三、运用学习心理,找对“引学”策略

数学学习的主体是学生.学生的心理状态对学习有十分重要的影响.了解学生学习心理,方可找到正确的“引学”策略：

1.创设情境,激发兴趣

“兴趣是最好的老师”.美国教育心理学家罗伯特•加涅[Robert Mills Gagné]认为：“教学活动是一种旨在影响学习者内部心理过程的外部刺激”.创设合适的教学情境能激发学生学习兴趣、激活学生思维.教师通过联系社会、生活实际,设计数学实验等方式创设学生感兴趣的学习情境,激发学生强烈的学习愿望,为实现对概念的摄取、理解、巩固、应用奠定基础.

例如在“指数函数”的教学中,我们创设如下实验情境：让每位学生做折纸游戏.并思考问题：(1)折纸的层数y关于折叠次数x的函数关系是什么？(y=2x);(2)折纸呈现的面积数y关于折叠次数x的函数关系是什么这两函数具有哪些相同的特征？(观察对比可得：都是y=ax这种形式,指数是自变量,底数是常数)(4)这样的函数给它起个什么名字好呢？(一般地,y=ax,a＞0,a=1叫做指数函数,它的定义域为ℝ)(5)请问我们可从哪些方面研究这类函数？(解析式、图象、定义域、值域、奇偶性、单调性、特殊点等.)

这样,学生在实验基础上展开相关问题的研究,渴求了解和掌握相关知识的欲望大增.我们通过问题引导,归纳出“指数函数”的概念,学生自然融入学习的情景之中,为实现对指数函数概念的摄取、理解、巩固、应用奠定了基础.

2.直观教学,形成概念

俄国心理学家谢切诺夫指出：“某一思想只有在它构成一个人自己有的经验中的一个环节时,才能被他领会或理解.”概念的摄取的过程即是概念映像在头脑初步形成的过程.在学习概念过程中,学生要用各种感官去感知概念,去听取教师的言语说明,去阅读文字符号,去进行实际操作,其目的在于了解概念的表征,有选择地把感知的概念的有关信息进行初步概括,形成表象.教学中,教师要运用教具、图表、多媒体等,加强直观教学,培养学生的形象思维,促进学生对概念的感知;注重运用强度律、差异律、对比律、活动律和组合律等感知规律有目的、有系统、有计划地组织学生进行观察,培养学生敏捷而准确的洞察力,获取信息,形成概念.

在讲授导数的几何意义时,我们开展了如下实验探究：

实验器材：铁线一条(l)、小线圈两个(A、B)、小绳一条(lAB)

实验过程：

1.将小绳穿过两个线圈(A、B),再将小线圈套到铁线l上(如图1),将线圈A固定于铁线上;

2.将B点慢慢向A点移动到如图2的位置;

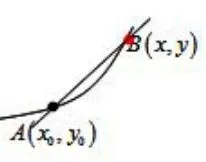
图1

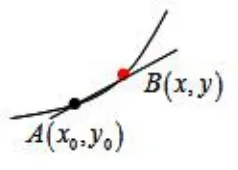
图2

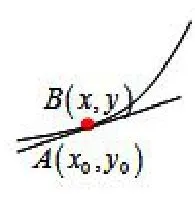
图3

3.将B点移动到A点与之重合如图3的位置;

4.可重复以上步骤,加深体会.

实验过程让学生体会到l的割线AB在变化运动中渐变成的切线过程(运用实物教具、多媒体动画演示)

不妨设l的方程为y=f(x),点A(x0,y0),B(x,y),其中割线AB斜率,结合导数的定义：即可以这样理解：.

由割线的斜率到切线的斜率,学生理解自然而然,对导数几何意义的理解水到渠成.

3.揭示联系,理解概念

理解是以已有的知识经验为基础的.根据美国著名学者奥苏伯尔的同化理论,任何一个新知识均可依附上位概念或下位概念作为新概念的支撑点,建立新概念与原有知识的联系,促进知识的正向迁移.为帮助学生透彻理解并掌握数学概念,教师要注意加强对数学概念的对比分析.如,在学习偶函数概念时,让学生对比分析：(1)函数f(x)=x2,(x∈(-1,2))的奇偶性;(2)函数f(x)=x2,x∈(-1,1]的奇偶性;(3)函数f(x)=x2,x∈[-a,a](a＞0)的奇偶性.学生在对比可发现：函数定义域关于原点对称是函数为奇(偶)函数的必要条件.

4.强化训练,巩固概念

美国著名心理学家斯金纳提出的“操作性条件反射”中,“强化”和“惩罚”是两个最基本的心理现象.学生的学习在师长与同学的赞扬、奖赏、获得成功愉悦感,则这些学习行为会得到“强化”;如果学生的学习行为伴随着另一种结果,比如疼痛或尴尬,那么今后在相似的情况下,他们将很少会再重复这一行为,这种现象被称为“惩罚”.

概念的应用是概念学习的最高层次.它使摄取、理解、巩固的概念得到检验和发展,是抽象知识化为具体行动的过程.为了引导学生理解并运用好念,我们注意做好如下三个方面：

1.设计对比练习,辩析概念例如,学生对两个函数相同的概念比较模糊,总以为定义域相同和值域相同的两个函数是相同的.教师可举反例：函数f(x)=(x+1)2,x∈{-1,0,1}与函数g(z)=(z-1)2,z∈{-1,0,1}的定义域相同,且值域都是{0,1,2},但它们的对应法则不同,是两个不同的函数.这样,加深了学生对函数的理解.

2．在知识交汇处设计练习,融会贯通.在解决一些情景复杂的问题中,单凭头脑中某一个或几个概念是无法进行的,审题时要找出其中明朗的和隐含的信息,依据这些信息向自己己有的认知网络系统靠近,从中找出结合点,并将这些结合点激活,重现所需概念.教学中应重视培养学生思维的广阔性和深刻性,使他们善于找出事物的本质属性.如：讲二次函数时,设计练习：当x为何值时,函数y=mx2+2x-1与x轴只有一个交点？许多学生不假思索地直接用∆=0,解得m=-1;默认y=mx2+2x-1必是二次函数,而忽略了m=0这种情形.这是对二次函数y=ax2+bx+c中a=0的本质属性认识不足造成的,教师教学中要把关键字词作标示,引起学生解题时注意,让答题时全面考虑问题.

3．从发展的角度设计练习,培养创新思维.有些概念是在特定的教学阶段中产生的,概念因此具有一定的局限性.随着认知进程的发展,概念的本质属性和非本质属性也随着发生了不同程度的变化,因此应用概念不能因循守旧,必须从发展的角度应用概念.

例(2009年陕西卷文科第10题)定义在上的偶函数f(x),对任意的有则( )

A.f(3)＜f(-2)＜f(1) B.f(1)＜f(-2)＜f(3)

C.f(-2)＜f(1)＜f(3) D.f(3)＜f(1)＜f(-2)

考题是单调减函数教材定义的等价形式,结合函数奇偶性得出答案A,既真正体现“源于教材,高于教材”的命题理念,又有效的考查了考生辨析问题和解决问题的能力.同年理科卷第12题呈现了单调增函数定义等价形式“(x1-x2)f(x1)-f(x2)＞0”,这些都是在教材核心概念的基础上稍加变形或类比而设计的试题,体现了命题者的智慧和创新能力,这是从发展的角度理解概念的典型范例.

“立体引学”让教师在教学中有所作为,给教师的发挥足够的余地;让学生展现自我、获得成功搭建了平台,给学生的思维发展创设了更广阔的空间;让师生互动更有效,给课堂注入了新的活力.