淤泥地层中压入式沉井挤土效应的有限元分析
易 琼, 廖少明, *, 朱继文, 徐伟忠
(1. 同济大学地下建筑与工程系, 上海 200092; 2. 上海城建市政工程(集团)有限公司, 上海 200065)
0 引言
由于地层的差异分布,传统沉井下沉施工中会出现突沉、下沉困难、沉井姿态偏斜等问题。为解决竖向地层差异性给沉井下沉带来的困难,压入式沉井这一改良沉井工法出现并得到应用。该工法通过由千斤顶组成的反力控制装置提供下压力,在适当取土的情况下将沉井平稳地压入土层内,从而保证下沉全过程的稳定。
压入法最早应用于沉箱法施工桥梁基础中,早在1989年于日本西高岛平高架桥下部工程施工时为解决场地狭小的问题就采用了压入开口沉箱法[1]。近年来,随着施工机械设备的发展,一些市政工程也采用了压入式沉井工法,其规模和深度呈不断增大趋势。国外方面,D.Allenby等[2]介绍了苏格兰某污水处理工程中4个采用压入法施工的沉井案例。T.G.Newman等[3]介绍了伦敦泰晤士环城水道延伸工程中隧道两端采用压入式沉井工法施工的工作井案例。国内直到近几年才出现了采用压入式沉井施工的工程。台北捷运系统芦洲线CL700A标联络通道的竖井受限于施工空间狭小,引进了压入沉箱工法进行施工[4]。采用顶管法施工的上海市污水处理白龙港片区南线东段输送管道工程,也在其中1个工作井采用了压入式沉井工法[5]。
与静压管桩施工相类似,压入式沉井在下沉过程中会产生一定的挤土效应,这是不同于普通沉井的一个较大区别。施工中若处理不当,沉井下沉过程中挤土造成的扰动甚至会引起周边地面和建筑物的破坏。如何评估与预测压入式沉井下沉过程中的挤土效应将是施工中的一个重点问题。当前压入式沉井在国内外的工程应用仍较少,相关的理论研究尤其是与挤土效应有关的研究不够成熟,目前的研究主要集中为对沉井施工过程的现场监测分析。如徐鹏飞等[6]结合上海市污水处理工程中的压沉法工作井实例,通过分析沉井压沉过程中周边土体及管线的监测数据探讨了其对周边环境的影响;黄丁等[7]针对同一工程实例,重点对侧摩阻力进行了现场监控。至于有关沉井下沉过程中所产生的挤土效应则可参考静压管桩的相关研究,主要分为数值模拟、试验及现场监测。数值模拟方面,由于涉及到大变形,传统的有限元方法不再适用,取而代之的是离散元、任意拉格朗日欧拉法(ALE)、耦合的欧拉-拉格朗日法(CEL)等方法。叶建忠等[8]通过二次开发二维颗粒流程序PFC2D对静压沉桩过程进行模拟,细观上揭示了桩端、桩周土体在桩土相互作用过程中的运动规律;周健等[9]通过对静压开口管桩沉桩全过程进行离散元数值模拟并与模型试验进行对比,研究了土塞形成规律及砂土变形机制;张明义等[10]采用位移贯入法模拟静力压桩,在数值模拟中考虑了弹塑性本构关系、大变形及桩-土滑动摩擦等问题;章文姣等[11]基于LS-DYNA,采用ALE方法模拟了开口混凝土管桩连续贯入粉土的全过程,得到沉桩过程中桩周土体应力、位移及沉桩阻力的变化规律;王建华等[12]采用CEL方法模拟钻井船插桩过程对邻近桩影响,通过与离心模型试验结果比较验证了利用CEL有限元数值方法分析钻井船插桩对邻近桩影响的可行性;J.Ko等[13]运用CEL法对开口钢管桩沉入砂土的过程进行了数值模拟,研究了管桩直径、冲击能量、土层弹性模量及沉桩深度等因素对土塞高度和最大径向应力的影响;闫澍旺等[14]应用CEL有限元法模拟了桶形基础自重下沉和液压下沉的过程,得到不同强度黏土中的下沉阻力和下沉深度的关系及土塞高度。试验方面主要分为室内模型试验和现场试验,雷华阳等[15]通过对PHC管桩沉桩过程进行现场测试,研究了在沉桩过程中的桩周孔压变化和土体位移分布规律。综上所述,数值模拟结合试验与现场实测是目前研究贯入问题的主流手段。
尽管目前已有大量关于桩体压入问题的研究,但由于沉井在尺寸规模上与桩有很大不同,相关结论不能简单照搬,故对压入式沉井下沉过程的挤土效应进行研究仍十分有必要。本文以压入式沉井为研究对象,依托温州市区某超深压入式沉井工程,分析沉井压入过程中土体运动的力学机制,并采用耦合欧拉-拉格朗日(CEL)法对沉井下沉挤土过程进行数值模拟,重点分析下沉速度、土体压缩性及隔离桩对挤土效应的影响。
1 工程背景
1.1 项目概况
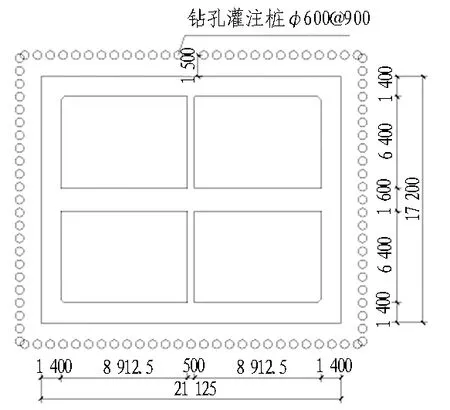
浙江省温州市鹿城区南塘街北入口改造工程中采用压入式沉井工法施工一地下16层立体停车库,为国内首次采用该工法进行地下车库施工。其中沉井结构采用矩形断面,尺寸为21.125 m×17.200 m,高度为34.05 m。长短边各设1道中隔墙将沉井分为4个井隔舱。此外,井壁外1.5 m处还设有一圈隔离桩用以减小沉井下沉对周围土体的扰动。沉井结构示意见图1。施工场地紧邻众多建(构)筑物,环境保护要求严格。周边环境示意如图2所示。
施工场地附近为古河道,根据地质勘察结果,场地自上而下主要为①1杂填土层、②1淤泥层、②2淤泥层、④11粉质黏土层、④12粉质黏土层、④2黏土层、⑤2黏土层等工程地质层。其中,②1、②2淤泥层厚度近25 m,是沉井下沉穿越的主要地层,且其呈流塑状,压缩性、灵敏度高,承载能力差,地基承载力仅40 kPa,属典型的软弱地基土,将给沉井下沉施工带来许多挑战。根据勘察报告,各土层的地质剖面及物理力学参数变化情况如图3所示。
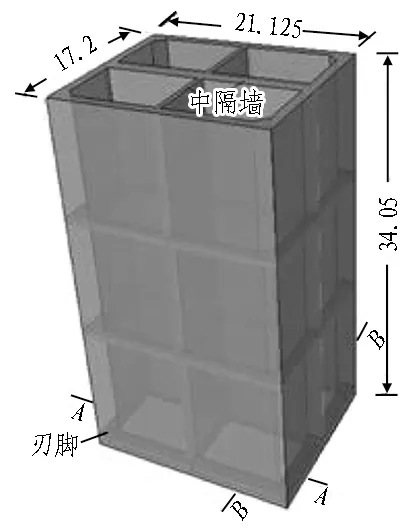
(a) 沉井三维示意图(单位: m)
(b) 沉井平面图(单位: mm)

(c) 沉井竖向剖面图(单位: mm)
图1沉井结构图
Fig. 1 Structure sketches of caisson

图2 沉井周边环境示意图(单位: m)
1.2 压入式沉井施工工艺
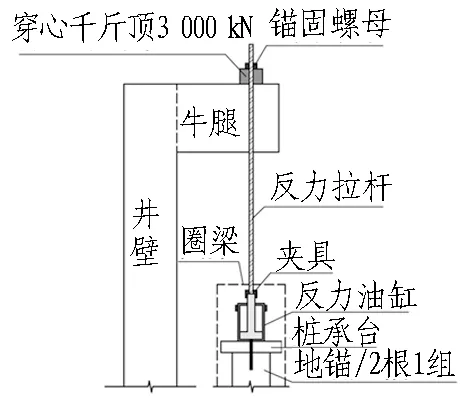
压入式沉井工法的特点在于有一套施加下压力的反力系统,主要包括穿心千斤顶、承压牛腿、反力拉杆、反力油缸、桩承台及反力地锚等。本工程沉井外侧4角对称布置16根直径为1 m的钻孔灌注桩作为反力地锚(2根1组,共8组),每组反力地锚分别与1个反力油缸相连,最大可提供3 000 kN的顶力。同时对称布置4对反力梁,每对反力梁由2个外伸承压牛腿组成。另外圈梁与沉井之间对称布置8个导向块,用以防止沉井下沉过程中发生过大偏斜。反力系统的平面布置如图4所示。
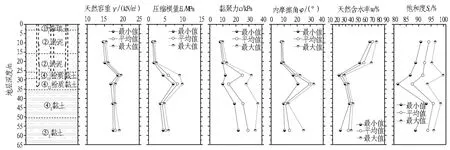
图3 地质剖面及地层参数示意图
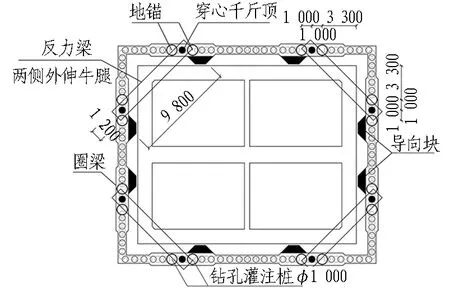
图4 反力系统平面布置图(单位: mm)
压入式沉井的施工流程为: 安装反力拉杆,将反力油缸与承压牛腿相连;反力油缸千斤顶将拉杆顶升一个行程(约80 cm)后锚固螺母将拉杆锁紧;反力油缸千斤顶带动反力拉杆缩回,将拉力传递至承压牛腿,使沉井受到压力下沉;当沉井下沉一个行程后,松开锚固螺母开始下一个行程的压入,重复上述步骤直至沉井下沉至牛腿接近圈梁时结束这一次压沉循环;拆除反力拉杆,切割牛腿,待下一节沉井结构施工完成后,再次安装反力拉杆将反力油缸与下一节的承压牛腿相连,开始下一次压沉循环。施工流程示意如图5所示。
(a) 安装反力拉杆

(b) 加压下沉到位
图5压入式沉井施工流程
Fig. 5 Construction process of press-in caisson
压入式下沉施工的原则是“先压入后取土”,即通过理论分析在井内预留适当高度的土塞后,进行主动压入下沉,直到千斤顶所提供的压入力无法继续将沉井压入下沉时,再进行井内取土调整井内土塞至合适高度后进行下一阶段压入。在下沉过程中,应尽量避免取土过多导致沉井下沉,确保每一次下沉都是压入力主导的主动下沉而不是自重引起的被动下沉。
每次下沉时沉井所需的压入力可通过下沉系数K1反算得到,下沉系数
K1=(N+G)/(Rf+Rr+Qr)。
(1)
式中:N为压入力;G为沉井自重;Rf为总侧摩阻力;Rr为刃脚阻力;Qr为浮力。
由此推导得到压入力
N=K1·(Rf+Rr+Qr)-G。
(2)
根据地层的物理力学参数及沉井结构尺寸可以得到沉井自重、侧摩阻力、刃脚阻力和浮力,将这些参数代入式(2)便能预估出给定下沉系数所需的压入力,为下沉施工提供参考。一般下沉系数为1.05~1.25时,沉井能够较为平稳地下沉。
2 沉井压入挤土引起的土体位移机制
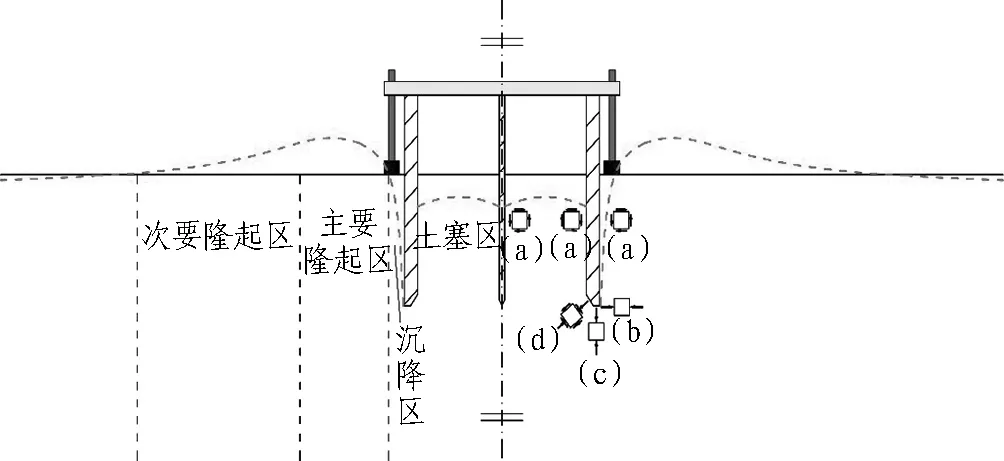
对于压入式沉井而言,在沉井下沉过程中,周边土体受到挤压会发生隆起变形,其大致形状可参考Meyerholf[16]提出的深层贯入所引起的土体位移模式。如图6所示,土体的变形情况表现为靠近沉井处的土体受到井壁摩擦力作用向下运动,稍远一点的土体由于挤压发生隆起变形,随着距离不断增大,隆起变形增大至最大值后逐渐减小。而由于沉井内部的隔舱尺寸较小,其内部的土塞会形成拱起状的土拱。根据地层变形情况可以将压入式沉井下沉的影响区域分为沉降区、主要隆起区、次要隆起区以及井内的土塞区。
一般来说,初始地层处于平衡状态,由沉井下沉引起土体的位移则可归结于土体中应力场的改变,即应力的增量。为探究压入式沉井下沉引起的土体位移的影响机制,需首先分析沉井下沉过程中不同部位的应力状态。
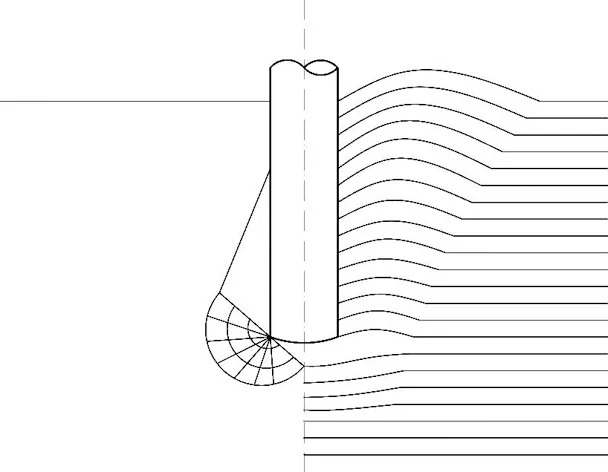
(a) Meyerholf位移模式
(b) 压入式沉井下沉挤土的地层变形
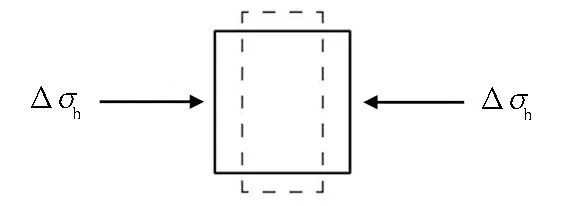
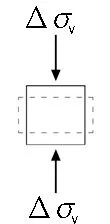
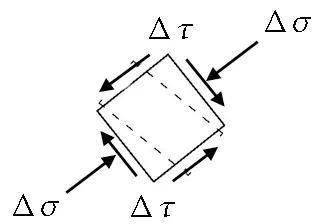
为明确沉井下沉产生的挤土效应的主要影响因素,这里仅考虑沉井下沉挤压土体引起的应力增量,忽略周边土体对挤压运动的约束作用。在压入下沉的过程中,沉井对土体的影响可分为4种情形: 浅层竖向剪切、深层水平挤压、底部竖向挤压及刃脚斜面挤压。不同情形引起的应力改变模式不同,如图7所示。
(a) 浅层竖向剪切
(b) 深层水平挤压
(c) 底部竖向挤压
(d) 刃脚斜面挤压
图7不同影响情形下的典型应力改变模式
Fig. 7 Typical stress variation patterns under different influences
下文分别具体分析图7所示几种情形下的应力应变情况。
2.1 浅层竖向剪切
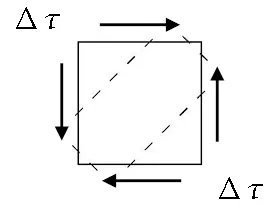
当沉井下沉至一定深度时,浅部地层内的结构对周围土体的作用主要表现为以摩擦力为主的竖向剪切作用,而几乎无水平向的挤压作用。这种作用在宏观上体现为邻近土体被沉井带动共同下沉,将其作用下的应力改变模式定义为浅层竖向剪切,其应力应变情形如图7(a)所示。
2.2 深层水平挤压
沉井底部的刃脚在下沉过程中会对土体产生显著的挤压作用,体现为土体被结构挤开产生塑性变形甚至剪切破坏,其位移模式可以简要看作是竖向挤压和水平挤压在不同程度上的叠加。其中水平挤压可类比孔扩张,其应力应变情形如图7(b)所示。
一般来说,水平向的应力增量会产生水平位移和竖向位移,当所需的竖向约束应力大于上覆土体自重应力时,该处土体就会产生向上隆起。
2.3 底部竖向挤压
刃脚一般由水平踏面和斜面组成,踏面的主要作用是在沉井停止下沉时提供承载力。正因如此,沉井下沉时对土体挤压最剧烈的位置便是在刃脚踏面正下方,主要是对土体产生竖向挤压作用,其应力应变情形如图7(c)所示。
竖向挤压导致的应力增量与自重应力不同,其大小主要与下沉速度有关。假定在下沉过程中的任意小的时间增量Δt内,沉井下沉使得刃脚踏面以下体积为V的微元土体由静止变为以相同下沉速度v向下运动,则根据动量定理有
F·Δt=mv。
(3)
其中微元土体的质量
m=ρV=ρvAΔt。
(4)
式(3)和式(4)中:F为刃脚对微元土体的竖向挤压力;v为下沉速度;ρ为土体密度;A为刃脚与微元土体的接触面积。
将式(4)代入式(3)可得
F=ρv2A。
(5)
于是有
(6)
式中Δσ竖向为竖向挤压应力增量。
式(6)表明,竖向下沉中刃脚踏面对土体的竖向挤压应力与土体密度及下沉速度的平方呈正比。
2.4 刃脚斜面挤压
相比于踏面,刃脚斜面处的土体位移情况较为复杂,简要的应力应变情形如图7(d)所示。
为分析压入式沉井下沉挤土效应的影响因素,下文对压入式沉井下沉中范围最广的典型影响模式,即浅层竖向剪切进行分析,其应力应变变化情况的相关公式如下。
Δσ1=Δτ;
(7)
Δσ3=-Δτ;
(8)
(9)
(10)
式(7)—(10)中: Δσ1为最大主应力增量; Δσ3为最小主应力增量; Δτ为切应力增量; Δε1为最大主应变增量; Δε3为最小主应变增量;E为土体弹性模量;ν为土体泊松比。
Δσ水平=KΔσ竖向=Kρv2;
(11)
Δτ=μΔσ水平=μKρv2;
(12)
(13)
式(11)—(13)中:Δσ水平为水平挤压应力增量;K为侧向土压力系数;μ为沉井侧壁与土体的滑动摩擦系数。
综上可知,压入式沉井下沉挤土影响下的土体位移规律主要与土体弹性模量E、泊松比ν、侧摩擦因数μ、侧向土压力系数K、土体密度ρ及下沉速度v等参数有关。
3 压入式沉井挤土效应的数值分析
3.1 有限元模型建立
为分析压入式沉井在淤泥地层中下沉所引起的挤土效应,采用ABAQUS有限元软件中的耦合欧拉-拉格朗日(CEL)方法对沉井的压入下沉过程进行数值模拟,重点分析下沉速度v、土体压缩模量Es以及隔离桩布设情况对压入式沉井下沉挤土效应的影响。
针对本工程特点和地质条件,采用如下简化假定和模拟方法:
1)由于沉井刚度一般远大于周边土体,可将其假定为刚体,并采用拉格朗日网格建模,单元类型为R3D4;
2)模型中仅考虑单一淤泥地层,采用Drucker-Prager弹塑性本构模型及欧拉网格建模,单元类型为EC3D8R;
3)采用耦合欧拉-拉格朗日方法(CEL)考虑土体的大变形问题,并采用罚函数约束来控制沉井与土体的接触耦合;
4)CEL方法的计算收敛性对网格密度的依赖较大,参考文献[11-14],欧拉网格尺寸选为沉井壁厚/6;
5)采用位移贯入法在沉井上施加匀速变化的位移曲线模拟整个下沉过程,下沉速度基准设置为0.2 m/d,下沉过程中井内不挖土,并假定整个下沉过程中结构保持垂直姿态。
建立的压入式沉井下沉模型如图8所示,沉井尺寸同图1。模型长150 m,宽120 m,高70 m。采用欧拉网格模拟土体,欧拉土体上方设置一个厚度为10 m的空物质层,以容纳地表土体可能发生的隆起变形。沉井初始位置位于模型表面正中心。

图8 有限元模型示意图(单位: m)
淤泥层的物理力学参数按实际土层厚度加权得到。鉴于温州淤泥层的特殊性,土体弹性模量E根据文献[17]并经试算后取E=5Es,泊松比ν取0.49,沉井结构的基准侧摩擦系数μ取0.3。由此得到的土体计算参数如表1所示。

表1 土体计算参数
根据第2节的分析,土体受沉井下沉挤土所产生的位移主要与下沉速度、土体压缩模量等因素有关。通过独立改变这些参数的大小进行多次计算,可得到挤土效应对这些参数的敏感性。主要以地表变形、深层土体水平位移及刃脚挤压应力作为判别挤土效应大小的指标,并与实测数据进行对比。其中背景工程的压入式沉井已下沉3.77 m,下沉时长18 d,平均下沉速度约为0.21 m/d。下沉期间,地表最大隆起为9.6 mm,发生在井外4.5 m处;最大沉降为0.9 mm,发生在井外27 m处;周边地表变形以隆起为主;地下污水管线最大沉降为16.9 mm;邻近建筑物的最大沉降为15.4 mm,最大差异沉降为5.5 mm,对应倾斜仅为0.000 6。从实际施工来看,压入下沉对周边管线及建筑物的影响较小,对环境的影响主要体现在挤土效应引起的地表不均匀变形。
3.2 有限元模型验证
文献[18]以上海地铁7号线某采用气压沉箱法施工的盾构隧道竖井为研究对象,通过现场实测和数值模拟探讨了施工对周边地层环境的影响。该气压沉箱长25.24 m、宽15.6 m、深29.06 m,与本文的压入式沉井在尺寸上较为接近。该工程整个施工过程的平均下沉速度约为0.2 m/d。同时,气压沉箱通过设置高气压限制周边土体进入井内,压入式沉井通过井内留土限制周边土体进入井内,二者施工引起的周边土体位移机制也比较类似。为验证本文数值模型的正确性,将下沉速度为0.2 m/d时数值模拟所得的地表变形曲线与文献[18]的研究成果进行对比,结果如图9所示。这里仅对比长边方向,并以各自的沉井长度为基准对横坐标的离井壁边距离进行归一化处理。

图9 压入式沉井与气压沉箱引起的地表变形比较
Fig. 9 Comparison between ground deformation induced by press-in caisson and that induced by pneumatic caisson
由图9可以看出: 本文模拟得到的地表变形曲线与文献[18]研究得到的地表变形曲线在变形趋势上拟合得较好,均为近处地表发生沉降而远处地表稍有隆起。不同点主要在于气压沉箱施工引起的地表沉降在影响范围和数值大小上都更大。这可能是因为气压沉箱主要通过高气压来平衡水压从而限制地下水进入井内,但仍会有部分土体在下沉时进入井内,进而造成周边地表有比较明显的沉降;而压入式沉井一是可以借由土塞自重平衡井外土压,二是由于沉井无底使得井内外地下水存在渗流通道,无论地层渗透系数如何最终井内外地下水位总会趋于一致从而平衡井外水压,因此能够大大减小周边地表沉降。尽管如此,本文模拟结果与文献[18]研究结果在数量级上是较为接近的,由此可认为本文所采用的有限元模型计算得到的结果是合理的。
3.3 下沉速度对挤土效应的影响
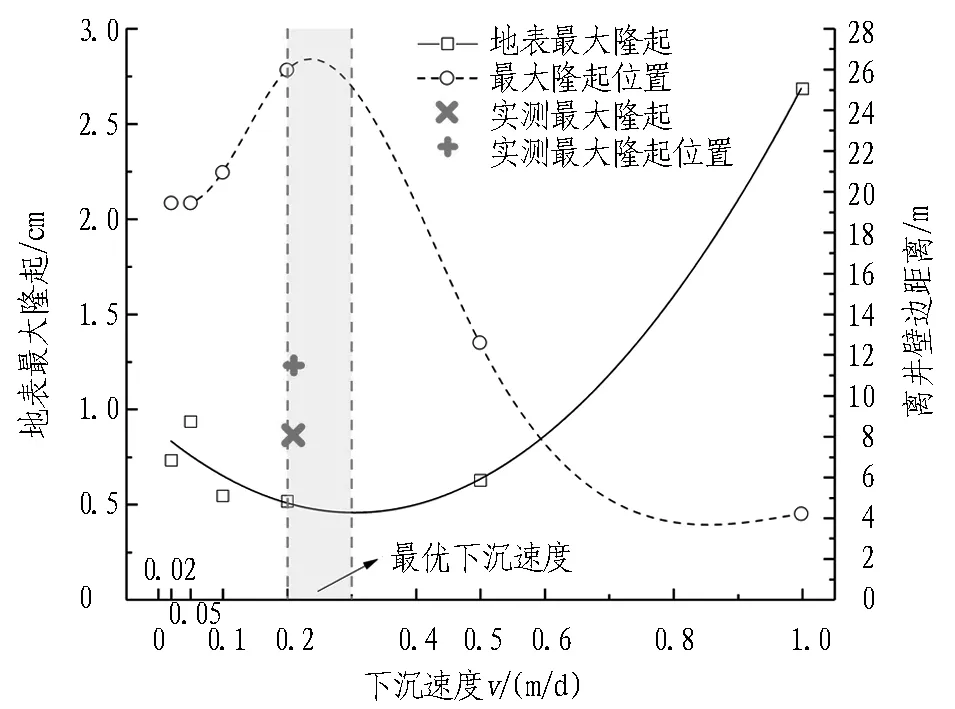
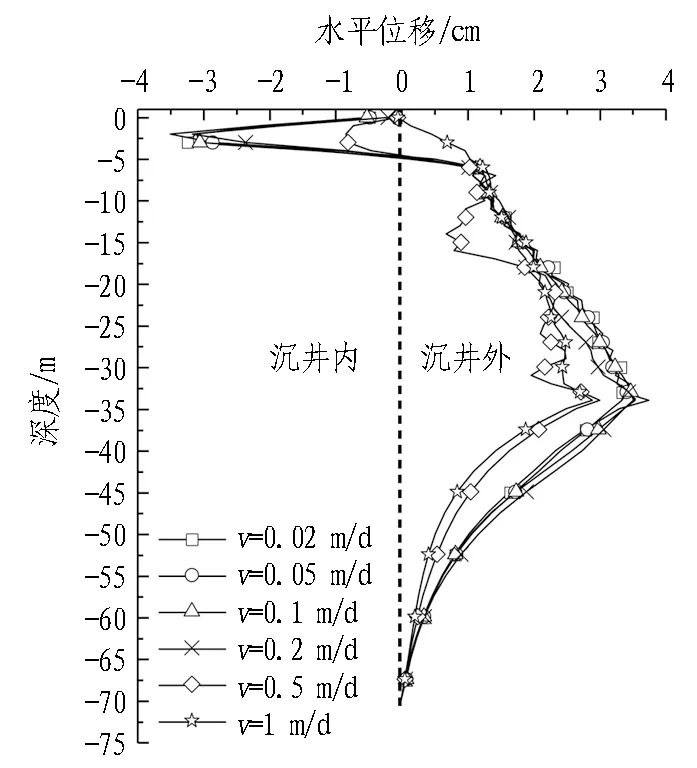
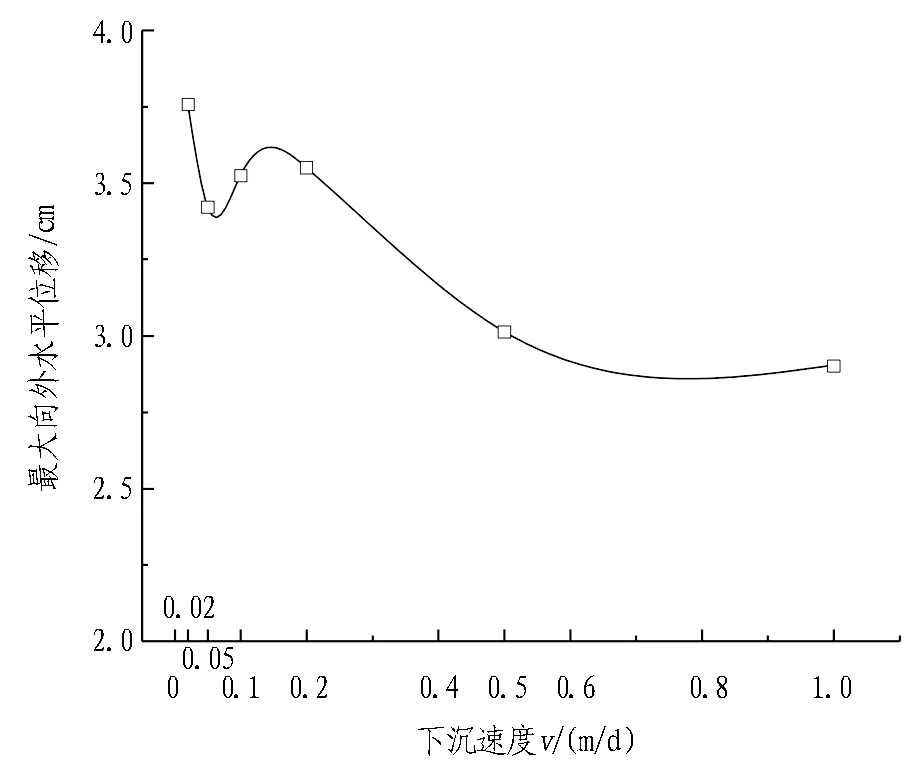
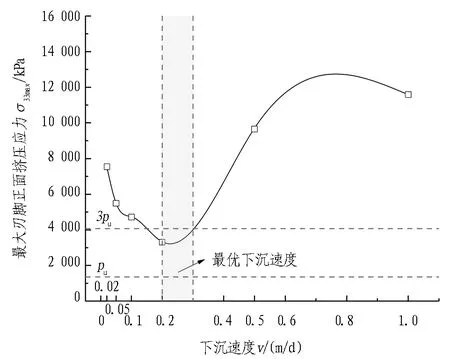
仅改变下沉速度,其他条件仍同标准情况一致,分别取下沉速度v=0.02、0.05、0.1、0.2、0.5、1 m/d进行计算分析,得到的地表变形、深层土体水平位移及刃脚挤压应力变化情况如图10—12所示。
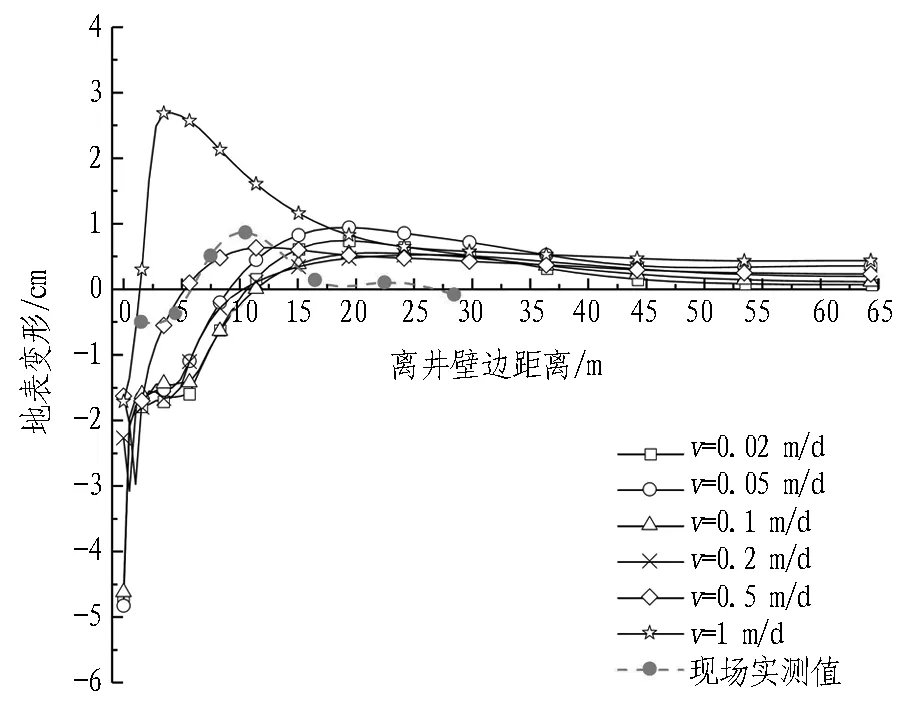
(a) 不同下沉速度的地表变形
(b) 不同下沉速度的地表最大隆起及对应位置
图10下沉速度对地表变形的影响
Fig. 10 Effect of sinking velocity on ground deformation
(a) 不同下沉速度的累计深层水平位移
(b) 不同下沉速度的最大向外水平位移
图11下沉速度对累计深层水平位移的影响
Fig. 11 Effect of sinking velocity on horizontal displacement along depth of soil
(b) 不同下沉速度的最大刃脚正面挤压应力
图12下沉速度对刃脚正面挤压应力的影响
Fig. 12 Effect of sinking velocity on vertical press stress of blade feet
1)由图10可知,随着下沉速度的增大,沉井下沉挤土引起的地表变形逐渐增大。地表最大隆起普遍为0.5~1.0 cm,且大多位于距离井壁边15~26 m(为0.4~0.8倍的下沉深度)处。而与实测相比,由于未考虑隔离桩影响,数值模拟所得的地表隆起偏小且离井壁偏远,即地表变形更为平缓。随着下沉速度的加快,地表的最大隆起逐渐增大,而最大隆起点离井壁的距离则逐渐减小。其中,当下沉速度为0.2~0.3 m/d时,地表的最大隆起最小且离井壁最远,即挤土引起的地表变形最平缓。因此,可以认为0.2~0.3 m/d是最优的压入下沉速度。
2)由图11可知,井壁边土体的深层水平位移随深度的增加而增大,在沉井设计下沉深度34.05 m附近达到最大值后逐渐减小,可见刃脚处水平挤土效应最大。然而下沉速度越大,最大水平位移反而越小。结合地表变形规律后可以发现,大于0.3 m/d后,下沉速度越大,竖向挤土效应越大,水平挤土效应越小。
3)由图12可知,刃脚正面挤压应力随下沉深度的增加呈抛物线增长,且在下沉速度为0.2~0.3 m/d时达到最小值。此时,刃脚挤压应力在1~3倍的地基承载力范围内,沉井可较为稳定地下沉。而当下沉速度为0.5 m/d以上时,刃脚挤压应力急剧增大,土体被严重破坏,此时沉井极易发生突沉。由于无法考虑土体破坏后的强度降低,数值模拟所得刃脚正面挤压应力仍在增长,实际工程中土体破坏后应力不可能继续增大。
3.4 土体压缩模量对挤土效应的影响
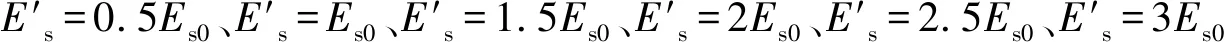

(a) 不同压缩模量的地表变形

(b) 不同压缩模量的地表最大隆起及对应位置
图13土体压缩模量对地表变形的影响
Fig. 13 Effect of compression modulus of soil on ground deformation

(a) 不同压缩模量的累计深层水平位移
(b) 不同压缩模量的最大向外水平位移
图14土体压缩模量对累计深层水平位移的影响
Fig. 14 Effect of compression modulus of soil on horizontal displacement along depth of soil

(a) 不同压缩模量的刃脚正面挤压应力
(b) 不同压缩模量的最大刃脚正面挤压应力
图15土体压缩模量对刃脚正面挤压应力的影响
Fig. 15 Effect of compression modulus of soil on vertical press stress of blade feet
1)由图13可知,随着土体压缩模量的增大,下沉挤土引起的地表变形整体上逐渐增大,而最大隆起点离井壁的距离则逐渐减小。其中,当压缩模量小于1.2Es0(约2.03 MPa)时,地表的最大隆起最小且离井壁最远,即挤土引起的地表变形最平缓。大于1.2Es0后,压缩模量越大,挤土效应引起的土体位移越大。
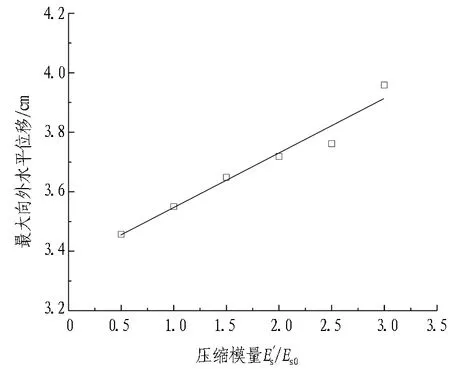
2)由图14可知,从井壁边土体的最大水平位移来看,最大水平位移随着压缩模量的增大近似线性增长,压缩模量增长2倍,水平位移增长约8.5%。结合地表变形规律可以发现,土体压缩模量增大,竖向和水平挤土效应都会增大。
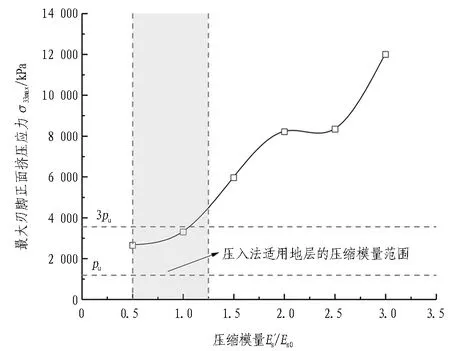
3)由图15可知,刃脚面挤压应力随着土体压缩模量的增大呈抛物线增长,且在下沉深度较大时增大趋势更明显。这是因为深度越大土体可进一步压缩的体积越少,压缩模量的影响越显著。其中,压缩模量小于1.2Es0(约2.03 MPa)时,刃脚挤压应力为1~3倍的地基承载力,地层较为稳定。
3.5 隔离桩对挤土效应的影响
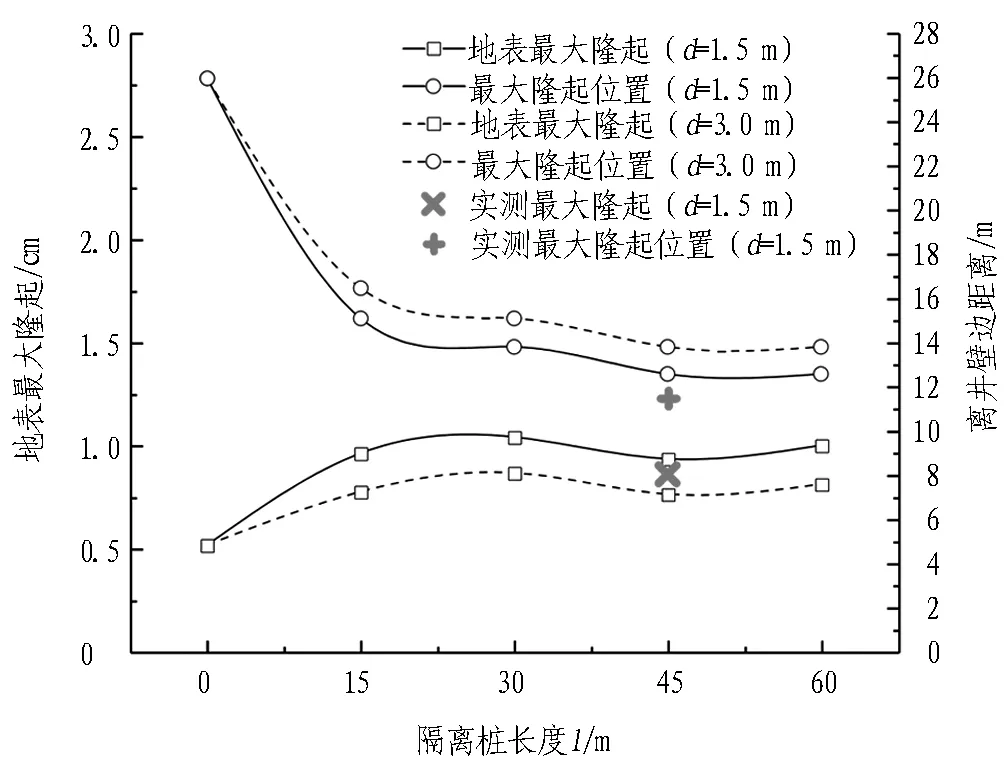
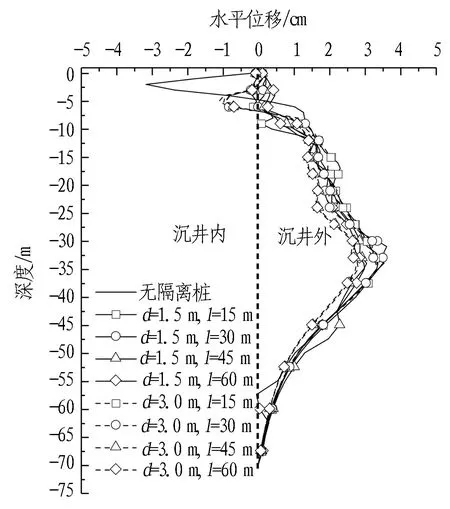
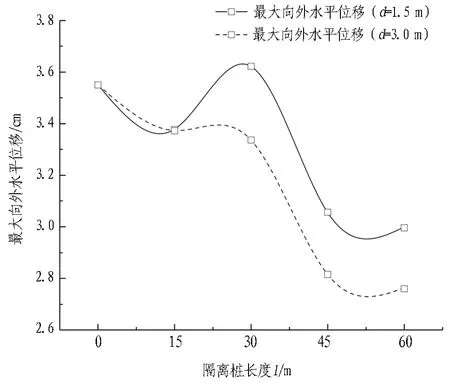
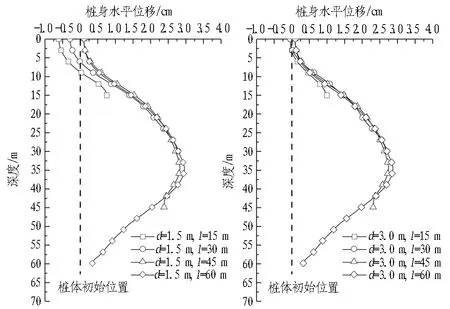
为减小沉井下沉对环境的影响,在沉井四周距井壁1.5 m处布设φ600 mm@900 mm灌注桩作为隔离桩,桩长45 m。为分析隔离桩对挤土效应的影响,分别取隔离桩与沉井外壁距离d=1.5、3.0 m,隔离桩长度l=15、30、45、60 m,共8种组合工况进行计算分析,得到地表变形、深层土体水平位移、隔离桩变形及刃脚挤压应力变化情况,如图16—19所示。
(a) 不同隔离桩工况的地表变形
(b) 不同隔离桩工况的地表最大隆起及对应位置
图16隔离桩对地表变形的影响
Fig. 16 Effect of isolation piles on ground deformation
(a) 不同隔离桩工况的累计深层水平位移
(b) 不同隔离桩工况的最大向外水平位移
图17隔离桩对累计深层水平位移的影响
Fig. 17 Effect of isolation piles on horizontal displacement along depth of soil
(a) 不同隔离桩工况的桩身水平变形

(b) 不同隔离桩工况的桩身最大水平变形
图18隔离桩变形情况
Fig. 18 Deformation of isolation piles
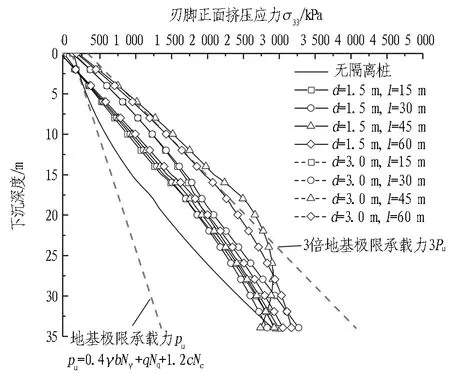
(a) 不同隔离桩工况的刃脚正面挤压应力

(b) 不同隔离桩工况的最大刃脚正面挤压应力
图19隔离桩对刃脚正面挤压应力的影响
Fig. 19 Effect of isolation piles on vertical press stress of blade feet
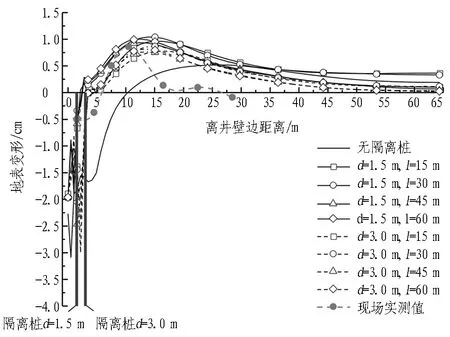
1)由图16可知,从地表变形来看,隔离桩对挤土效应引起的土体位移起到了一定的遮拦作用,使得靠近井壁的沉降和远处的地表隆起都大大减少。其中当距井壁较近时,数值模拟与实测所得的地表变形较为吻合。另外,隔离桩距离井壁越近、长度越大,近处的地表隆起越大而远处的地表变形越小,即挤土引起的地表变形越陡峭。因此,若场地内较为空旷,应将隔离桩布置得较近以减小远处地表变形;若场地内有重要管线及构筑物,则应将隔离桩布置得较远以减小场地内的地表差异变形。
2)由图17可知,从井壁边土体的深层水平位移来看,只有当隔离桩长度大于沉井最终下沉深度时,土体的最大水平位移才会有所减小,比起无隔离桩情况减小约20%。
3)由图18可知,从隔离桩的变形情况来看,上部向内变形而下部则向外变形,最终变形最大的部位则是在对应最终设计下沉深度即34.05 m左右。因此,隔离桩只有在桩长大于沉井下沉深度时才会对挤土效应起到较好的遮拦效果。
4)由图19可知,由于隔离桩的遮拦作用,受到挤压的土体难以发生向外的变形和位移,导致土体中增加的应力无法释放。以刃脚正面挤压应力为例,隔离桩距井壁越近、长度越大,沉井压入下沉对土体的挤压应力就越大。
4 结论与建议
针对压入式沉井下沉特点,分析了沉井下沉挤压对周边土体应力状态的影响,并采用耦合欧拉-拉格朗日(CEL)法对沉井的压入下沉过程进行模拟,研究压入下沉在淤泥地层引起的挤土效应,得到的结论与建议如下。
1)压入式沉井下沉产生的挤土效应使得周边地层发生4种典型变形,分别是井内土塞区的土体两边被井壁带动向下而中间稍有拱起;井外沉降区的土体由于靠近井壁被带动向下运动从而引起地表沉降,范围为0~0.4倍的下沉深度;稍远一点的主要隆起区的土体受到挤压向上隆起,范围为0.4~1.2倍的下沉深度;再远一点的次要隆起区的土体则向上小幅隆起。
2)下沉速度越快,竖向挤土效应越大而水平挤土效应越小,体现为地表隆起越大而深层水平位移越小。由于挤土效应增大,沉井刃脚对土体的挤压应力也会显著增大。从减小地层变形及控制刃脚挤压应力的角度来看,最优的压入下沉速度为0.2~0.3 m/d。
3)土体压缩模量增大,竖向和水平的挤土效应都会增大,体现为地表隆起和深层水平位移的相应增大,且刃脚正面挤压应力也大大增加。为减小压入下沉中挤土效应的不利影响,压入下沉适用地层的压缩模量应小于2.03 MPa。
4)隔离桩对挤土效应引起的土体位移可以起到一定的遮拦效果,距井壁越近、桩长越大,效果越好。从控制地层变形方面来考虑,场地内空旷时应将隔离桩较近布置;而场地内有重要管线时则需将隔离桩较远布置。
5)为控制挤土效应,建议压入式沉井施工在遇到高压缩性的软弱地层(如淤泥层)时以压入为主,而在遇到较坚硬的地层时则应更多进行井内取土辅助压入。
6)本文采用CEL法模拟压入式沉井下沉过程,可以较为准确地得到挤土效应所引起的地层变形情况;但没有考虑周边既有建筑物的影响,且CEL法对于地层应力及接触应力的计算并不准确,还需进一步与现场实测进行对比分析。

