基于CFD的散货船纵倾优化研究

马儒昆，胡 义

(武汉理工大学 能源与动力工程学院，湖北 武汉 430063)

由经济飞速发展带来的负面影响已经渐渐地影响到了地球上所有生物，酸雨、雾霾、水污染、能源匮乏等都变成了亟待解决的问题。在存在污染的全部行业里，如果污染占比高达10%的航运业能够采取真实有效的措施进行节能减排，对于改变环境污染、能源枯竭的现象无疑是一个福音。

一直以来航运业都在采取着各种各样的方法力求能够在节能减排方面有所进步，比如船舶航线的优化、气泡减阻、应用太阳能、风能等新能源、应用船舶电推系统等，但以上措施往往需要投入更大的成本，同时由于船型的限制，成效并不与投入成正比，因此对新旧船舶而言都不具备普遍推广性。我们对船舶航行过程中阻力因素进行思考，提出一个高效且适用性广的措施——纵倾优化。船舶航行水动阻力受航速、排水量、吃水和纵倾角度的影响，通过调整纵倾浮态，改变船舶航行时的水下形状，进而影响兴波、船身湿表面积、船首来流、船尾去流等船舶阻力决定因素，就能够有效减少航行阻力，降低主机功率需求，减少燃油消耗。

如果不考虑水深影响因素，不同类型的船舶在已知航速和排水量工况下，都会有一个最优纵倾值，使船舶能够在更小的阻力下航行。研究纵倾通常使用的方法有模型试验和CFD数值仿真。相对于模型试验，在如今计算机性能较以前大幅提高的情况下,CFD数值仿真不仅能节省大量的工作量以及资金的投入，得到的仿真结果也在可靠的范围之内。

1 控制方程和湍流模型

船舶在海平面航行的问题，涉及阻力、流动分离、复杂的流态变化，必须考虑黏性的影响。黏性流体的基本方程是纳维-斯托克斯(Navier-Stokes)方程，简称N-S方程。考虑微元体不可压缩性并基于质量守恒定律，得到直角坐标系下的连续性方程：

(1)

式中：vi表示在直角坐标系xi下流体速度的分量(i=1,2,3)。

基于广义牛顿内摩擦定律，引入一般形式的流体运动方程，常用黏性不可压缩流体的N-S方程为：

(2)

式中：t为时间;ρ为流体密度;p为流体压力;μ表示流体分子运动黏性系数;fi为流体体积力分量;xj代表空间坐标分量。

(3)

对于湍流瞬时速度有：

(4)

质量守恒方程的时均为:

(5)

湍流平均运动的动量方程，亦即时均化的N-S方程(雷诺方程)为:

(6)

k-ω湍流模型对自由剪切湍流、附着边界层湍流和适度分离湍流都有较高的计算精度，可以较好地反映雷诺应力随空间和时间的变化规律。而k-ω模型主要又分为标准的k-ω模型和SSTk-ω模型。对比标准k-ω模型，SSTk-ω模型使用了不同的模型常量，在湍流黏度上考虑了湍流剪应力的传播，合并了来源于w方程中的交叉扩散，这些改进使得SSTk-ω模型在广泛的流动领域中有更高的精度和可信度。因此，本文选用SSTk-ω湍流模型求解RANS方程[2]。

2 船舶阻力数值计算

试验船模系木质制造，表面喷漆上蜡，缩尺比λ=20.729。按缩尺比进行换算后得到设计吃水状态船舶主尺度，如表1所示。

表1 船舶主尺度

2.1 船体模型的建立

船体模型按1∶1在Creo5.0中建立，主要步骤是导入点数据—连点成线—曲面建模—封闭曲面的实体化。具体方法是通过读取船体型线图得到.pts格式的点文件，然后将这些点数据导入Creo5.0中，通过曲线命令构建出船体外表面轮廓，再通过边界混合命令连线成面，得到封闭的船体外壳整体，最后进行壳模的实体化操作。得到船模如图1所示。然后将模型导入到ANSYS Workbench当中建立仿真模拟的流场区域。流体分为上层的空气域和下层的水域，入口在距船首1倍船长处，出口在距船尾2倍船长处，水域底面在距船底表面0.5倍船长处，空气域顶面在距船上甲板0.25倍船长处，流域两侧面在距船体纵中剖面1倍船长处。在Workbench中绘制好的计算区域如图2所示。

图1 船模

图2 计算流域

2.2 网格划分与边界条件

网格划分的主要思想是有限体积法，网格划分细致可以保证计算域的收敛、节约收敛时间以及使计算精度在可靠的范围之内，但是过分细致的网格对计算机的性能要求极高，并且我们并不需要通过耗费大量的时间和计算资源来得到精度上微小的改善。因此在对计算流域进行网格划分时，对船首和船尾参数变化梯度大的部分，要保证有细密的网格，但是中间的船身部分可以使网格相对平缓、均匀分布；流体区域在船体附近会有冲击，因此靠近船体的流场和自由液面部分的网格需划分更细致，而远离船体的流场网格可以较为平缓稀疏。远离船体的空气域和水流域整体上使用六面体网格，靠近船体部分的流域组合使用六面体网格和四面体网格，并局部加密[3]。网格质量要满足计算要求，避免负体积网格出现。划分好的网格如图3所示，网格总数约为144万。

空气和水的入口设置为速度入流边界条件，顶面及出口设置为压力出口，流域两侧面和底面设置为壁面，定义船体表面为壁面边界条件。

图3 网格划分

2.3 平浮状态数值计算结果与船模试验结果对比

本文船模实验结果来自于上海船研所《10 000DWT散货船快速性模型试验研究报告》。其中阻力试验采用电测阻力仪和天平混合计测系统测试，由计算机实时采样记录船模速度、船模阻力。模型缩尺比为λ=20.729，数值计算模型与船模尺寸保持一致。CFD数值计算采用的湍流模型为SSTk-ω模型。

设计吃水6 m、纵倾角为0°状态阻力试验，将船模试验结果与Fluent数值计算结果进行对比，如表2所示。为更直观显示，将结果绘制成如图4所示折线图，其中横坐标为傅汝德数(Fn)，纵坐标为船舶所受阻力值(简称Rtm)。经对比可以发现，CFD数值计算阻力值随航速变化趋势与船模试验阻力变化趋势一致，而平浮状态时Fn越小(对应船速越小)，两者的结果差异越大，当Fn为0.145时，数值计算结果较之模型试验结果相差7.51%。当Fn为0.190时，船模试验结果与CFD数值计算结果基本保持一致。对比误差与变化趋势，可认定数值计算是一种切实可行的船舶阻力计算方法，可在实际进行船模阻力试验之前大量采用以估算船舶阻力。

图4 船模阻力与数值计算结果对比

3 不同纵倾下船舶阻力数值分析

下面通过改变船舶纵倾，即船舶存在艏艉吃水差的工况，以同样的方法进行船舶阻力的数值模拟。设计实验的倾角分别为艏倾1.0°、0.8°、0.6°、0.4°、0.2°，艉倾1.0°、0.8°、0.6°、0.4°、0.2°。在相同湍流模型、相同航速下模拟计算不同纵倾的船舶阻力，将纵倾船舶阻力与平浮状态下的阻力值对比，阻力值小于平浮状态结果为正，反之为负，得到图5所示的对比结果。其中，角度值为正代表艏倾、为负代表艉倾，0°表示平浮状态。

表2 数值计算与船模阻力结果对比

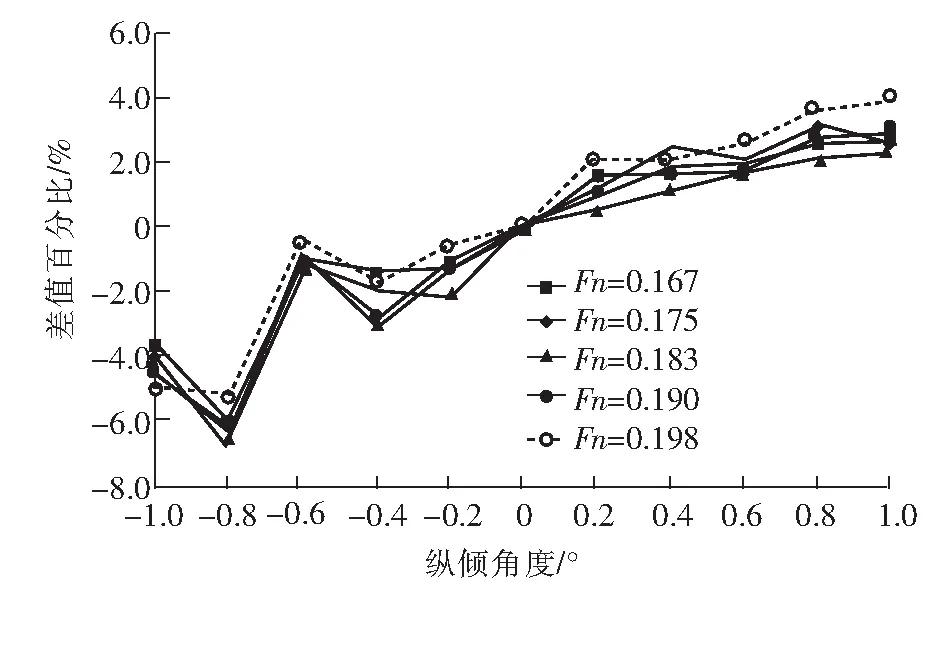
图5 不同纵倾阻力值对比

对比计算结果我们发现，艏倾和艉倾对于船舶阻力的影响明显不同。艏倾状态时，船舶所受阻力较平浮的要小，艉倾使船舶所受阻力变大。根据CFD数值计算结果，Fn=0.167时，艏倾角0.8°,阻力减小最多，达2.6%；Fn=0.175时，艏倾角0.8°,阻力减小最多，达3.1%；Fn=0.183时，艏倾角1.0°,阻力减小最多，达2.8%；Fn=0.190时，艏倾角1.0°,阻力减小最多，达3.0%；Fn=0.198时，艏倾角1.0°,阻力减小最多，达4.0%。对比不同航速时船舶所受阻力值，可为船舶提供如下航行建议：艉倾不利于减阻，出于经济性考虑的航行状态应避免艉倾；在各设计航速下应采取阻力减小最多的艏倾角航行。由此可见，在船舶营运过程中通过在稳性允许的范围内对船舶纵倾进行调节以减小阻力，可明显减少油耗成本，实现经济、环保作业。

已有航运企业根据CFD仿真模拟和水池实验、实船试航的论证结果，于实际作业中采用纵倾优化技术，取得了可喜的节能效果。中海集装箱运输股份有限公司(简称中海集运)根据实船报告，对14 100 TEU型船舶采用将原先艉倾改为艏倾的航行方案，考虑实际营运中海况及恶劣气象的影响，全年平均节能率高达5%以上。以中海集运2条航线(AEX7和AMA)运营的8艘14 100 TEU为例，并以5%的节能率计算，每年可节省燃油费用1 044万美元[4]。

4 船舶阻力数值计算二次开发

对Fluent进行二次开发，使用VB.NET搭建界面友好的框架，调用并传输数据，实现数值计算自动化运行，只需要输入少量的船舶运行工况数据，即可完成船舶阻力计算，使工程计算更加简单智能，可为船舶行业工作者节约大量时间精力。图6为船舶阻力数值计算二次开发的设计流程图。

图6 船舶阻力数值计算二次开发设计流程图

如图6知，第一部分工作是在Creo中进行模型的建立。首先建立船体模型，通过读取船体型线图建立.pts格式的点文件，然后将这些点数据导入Creo5.0中，通过曲线命令构建出船体外表面轮廓，再通过边界混合命令连线成面，得到封闭的船体外壳整体，最后进行壳模的实体化操作。Creo5.0提供很多二次开发的接口，如VB API、ProToolkit、J-Link等，通过二次开发可根据船舶轮廓点数据快速生成几何模型，极大的提高设计人员的工作效率。

第二部分工作的目的是为了得到计算流域的.msh文件。这部分工作主要使用Workbench来完成，但Workbench的二次开发不易完成，由于Workbench本身是一个集成平台，相关研究做的很少，因此这部分内容需要依靠人工去完成。

第三部分是Fluent二次开发。首先在输入界面打开第二部分工作得到的.msh文件，而后运行批处理文件(.bat)以唤醒Fluent软件，识别并读取日志文件(.jou)，按照命令完成处理和计算。可在输入界面上更改湍流模型、缩尺比、航速、时间、迭代步数，改变参数之后的临时文件对Fluent日志文件进行覆盖，加载求解完成后，调取结果文件返回到结果显示界面[5]。

5 结束语

本文以1万t散货船为研究对象，以CFD数值仿真工具Fluent为手段，采用VOF方法计算自由面[6]，求解RANS方程，对船体黏性流场进行阻力预报，将仿真得到的船舶阻力结果与船模试验结果进行对比，验证CFD数值仿真方法的正确性[7]。然后在稳性允许范围内，对比不同纵倾下的船舶阻力值，为散货船的纵倾优化提供指导，具体结论有以下3点。

1)将CFD数值模拟的计算结果与平浮状态的船模试验结果进行对比，验证了数值计算方法的可靠性。进行船模试验前预先用数值模拟方法进行方案的比较优化，再开始船模试验，可大量减少试验费用。

2)对散货船设计吃水、设计航速进行不同纵倾下的CFD数值计算。结果表明，使船舶艏倾可以减少该散货船航行阻力，而艉倾使船舶阻力增加。由此可见，平浮并非最经济环保的航行状态，艏倾可提高船舶阻力性能。

3)提出一种可实现的船舶阻力数值计算二次开发设计，使整个过程更加智能、高效。通过更改相关船模尺寸、航行工况参数将此二次开发应用到不同的船舶上，可计算出不同船舶的阻力结果，并得到纵倾优化的建议。