基于亚波长矩形孔阵列的偏振实验设计

张 勇，李先科，杨 澜

基于亚波长矩形孔阵列的偏振实验设计

张 勇，李先科，杨 澜

（南京工业大学，数理科学学院，江苏 南京 211816）

基于表面等离激元理论的科研成果，设计亚波长金属矩形孔阵列结构的偏振片，在微波段实现了偏振过滤和偏振旋转效应。利用单层金属矩形孔阵列的偏振片验证偏振过滤效应和马吕斯定律；利用双层金属矩形孔阵列的偏振片实现15°、30°、45°、60°、75°和90°的偏振旋转。该实验既可以弥补理工科相关课程中偏振实验的缺乏，又有利于学生了解学科前沿，有助于培养和提高学生的综合科学能力和素质。

偏振过滤；马吕斯定律；偏振旋转；表面等离激元；微波段

偏振是指波的振动方向相对于传播方向的不对称性，是横波区别于纵波的最重要的特征。电磁波是典型的横波，电磁波的偏振在许多课程中都是重要的内容，但是，长期以来电磁波偏振相关的实验课内容却偏少。

本文基于表面等离激元的最新研究成果，利用亚波长金属矩形孔阵列，设计了微波段的2个偏振相关的实验，分别实现了偏振过滤和偏振旋转效应。相较于传统的光波段的偏振实验，本文的微波段偏振实验具有如下优点：首先，可以直观看到偏振片和偏振旋转器件的微结构（即：单层和双层的金属矩形孔阵列）；其次，入射和透射偏振波的偏振方向可以通过发射端和接收端的喇叭天线直观地观察到；最后，可以对偏振过滤和偏振旋转的效应进行定量分析。

1 实验原理

金属是导体，其导电性能源于其拥有大量的自由电子。当电磁波辐射到金属表面时，由于电磁场与金属表面自由电子振荡的强烈耦合，电磁波能够沿着金属表面传播，这一电磁表面模被称为表面等离激元。基于表面等离激元理论，利用亚波长的金属微结构可以引导和控制电磁波的方向，从而使电磁波在金属微结构中传播时产生了许多独特的现象，例如：增强透射效应、增强分子荧光、负折射现象、逆多普勒效应、光学隐身等[1-3]。

1998年，Ebbesen等[4]的实验研究发现，光波段的电磁波照射到具有亚波长圆孔阵列的金属薄膜时，其最大透射系数比经典物理学的预测值高出2~3个数量级，这一现象被称为增强透射效应。实验的透射谱中通常具有多个透射峰和透射谷。理论研究认为，透射谷源于Wood异常，其波长dip由下式确定：

透射峰的波长peak则取决于表面等离极化激元模（SPP模），即peak由下式确定：

这里：m和n分别为金属和介质的电容率。

Molen[5]和Koerkamp[6]等研究了小孔的形状对增强透射的影响，研究发现，对于金属矩形孔阵列，只有偏振方向沿矩形孔短边的电磁波可以透射，而偏

振方向沿矩形孔长边的电磁波则不能通过。显然，这一现象类似于偏振片的性能。故可以利用具有矩形孔阵列的金属片来模拟偏振片的偏振过滤效应。此外，我们的研究发现[7]，利用两块具有矩形孔阵列的金属片，可以实现90°的偏振旋转。当然，利用单层或多层的矩形孔阵列也可以实现偏振旋转[8-9]。本文把科研成果转化为实验教学内容，设计单层和双层的金属矩形孔阵列，分别实现微波段的偏振过滤和偏振旋转效应。

2 实验设计

2.1 偏振过滤实验设计

基于亚波长金属矩形孔阵列的偏振片的结构示意图见图1(a)，亚波长的矩形孔周期性地排列于金属片之中。单个矩形孔的结构见图1(b)。单胞（或周期）的长和宽均为，矩形孔的长为，宽为，金属片的厚度为。实验制作的基于矩形金属孔阵列的偏振片如图1(c)所示。实验中，=60 mm，=40 mm，=10 mm，=1 mm。

图1 亚波长金属矩形孔阵列构成的偏振片

实验装置的示意图如图2所示，实物图见图3。该装置包括：用于测量透射电磁波的振幅透射率的矢量网络分析仪（型号：AV3629A）1台，2根用于传输电磁波的电缆线，2个用于发射和接收电磁波的宽带双脊喇叭天线（型号：GJ-WDRHA-01/12-N）。发射和接收的电磁波的偏振方向（或电场方向）都沿图3(b)所示的箭头方向，即喇叭天线截面的短边方向。实验中，可以通过在竖直平面内旋转喇叭天线来发射和接收不同偏振方向的电磁波。

实验时，按照图2的装置示意图连接好实验装置。样品置于两个喇叭天线之间。入射电磁波的频率的范围为2~5 GHz，对应的波长的范围为：60~150 mm。显然，实验中制作的矩形孔的周期的尺寸是亚波长的，即：<。对于亚波长的结构，其远场透射谱中，通常只有0级衍射，且0级衍射波的传播方向垂直于样品的表面，其他高阶衍射（如：±1，±2，±3…级衍射）都是近场的消逝波。

图2 偏振过滤及偏振旋转实验装置示意图

2.1.1 观察偏振过滤效应

为了观测偏振过滤效应，要测量图1中和两种偏振下的透射系数。为此调整接收天线的偏振方向，使其分别沿图1(a)中轴和轴方向，从矢量网络分析仪（图3(a)）中读出透射波的电场强度的透射系数ii=i/i0（偏振为t=E/x0；偏振为t=E/E0）。其中，E0(=,)为入射电磁波的电场强度；E(=,)为透射电磁波的电场强度。相应的功率透射系数定义为

矢量网络分析仪测量得到的偏振和偏振的透射系数随频率的变化关系见图4(a)。可以看出，偏振完全被抑制，其透射系数几乎为零；偏振则存在一个透射峰，这一透射峰源于SPP模（见式（2））。透射峰的波长为3.49 GHz，透射效率高达0.972，即97.2%的入射偏振光都可以通过。在透射峰位置处，金属矩形孔阵列呈现出明显的偏振过滤的现象，故这一结构可以用来制作偏振片。对于这一由矩形孔阵列构成的偏振片，其透振方向沿轴方向。

偏振片的性能可以用消光比[extinction ratio（ER），单位为dB]描述，即：

图4(b)为消光比ER随频率变化曲线。可以看出，在整个频率范围内，消光比都大于100 dB，最大消光比甚至超过180 dB。而通常的偏振的其消光比都低于100 dB[10-12]。显然，这一基于金属矩形孔阵列的偏振片具有良好的偏振过滤性能。

图4 x偏振和y偏振电磁波的透射系数和消光比随频率f变化曲线

2.1.2 验证马吕斯定律

马吕斯定律是指：当线性偏振波通过偏振片时，其透射波的强度满足下式：

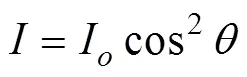
其中0为入射线偏振波的强度，为透射线偏振波的强度，为入射波偏振方向和偏振片透振方向的夹角。如果用透射系数表示，马吕斯定律可以表示为=/0=cos2。

实验中，样品和接收端的喇叭天线（图（2）中右边的喇叭天线）不动，接收端喇叭天线偏振方向始终沿轴方向。通过转动发射端的喇叭天线（图（2）中左边的喇叭天线）来产生不同偏振方向的入射波，使入射波偏振和偏振片的透振方向（即矩形孔的短边方向）的夹角分别为10°、20°、30°、40°、50°、60°、70°、80°和90°。对于每一个夹角，利用矢量网络分析仪来获得透射波的透射系数，结果如图5所示。

从图5可以看出，测量结果与马吕斯定律符合得很好。例如：当=0°时，峰值透射系数为0.983，接近于马吕斯定律（公式（5））理论值1，考虑到实验中不可避免的样品制作误差和测量误差，实验与理论值符合得很好；当=30°时，根据马吕斯定律，透射效率为0.75，而实验测得的峰值透射效率为0.742；当=60°时，理论透射效率为0.25，实验测得的峰值透射效率为0.241，同样符合得很好。也就是说，对于微波段的、基于单层矩形孔阵列的偏振片，其透射规律满足马吕斯定律。

2.2 偏振旋转实验设计

利用具有矩形金属孔阵列的双层金属片可以实现

图5 入射波偏振方向与透振方向不同夹角下透射效率随频率变化曲线

偏振旋转效应。能实现偏振旋转效应的结构称为偏振旋转器。实验中用到的偏振片与图1中用到的偏振片具有相同的尺寸。为了实现偏振旋转实验，制作3种矩形孔取向不同的矩形孔阵列结构的偏振片，如图6所示。图6(a)的偏振片的矩形孔长边与偏振片底边的夹角为45°，图6(b)中的夹角为60°，图6(c)中矩形孔的长边沿竖直方向。

图6 不同取向的矩形孔阵列的偏振片

实验时，利用图6中的2块偏振片构造偏振旋转器，两块偏振片中对应的矩形孔的夹角为，如图7(a)所示，该角度即为入射线偏振波透过双层偏振旋转器后的偏振旋转的角度。例如：两块图6(c)的偏振片可以构成0°和90°的角；利用图6(a)和(b)的偏振片可以构成15°和75°的角；利用图6(b)和(c)的偏振片可以分别构成30°和60°的角；利用图6(a)和(c)的偏振片可以构成45°的角。

需要强调的是，如果把两层金属片的矩形孔投影到同一个平面内，则对应的矩形孔是在底边处重叠，而不是在矩形孔的中部重叠，如图7(a)所示。作为例子，图7(b)和(c)展示了=90°时的双偏振旋转器的俯视图和侧视图。

图7 偏振旋转器的两层金属片中对应的矩形孔夹角和φ=90°的偏振旋转器

利用图2的实验装置测量不同偏振旋转角度下的透射系数。发射端的喇叭天线发射的电磁波的偏振始终如图7(a)中上层金属片中矩形孔的短边（即上层偏振片透振方向）平行，接收端的喇叭天线的偏振方向与下层金属片的矩形孔的短边（即下层偏振片透振方向）平行。两层金属片的矩形孔之间成角。这样，通过偏振旋转器的电磁波的偏振发生了角的旋转。测量结果见图8。

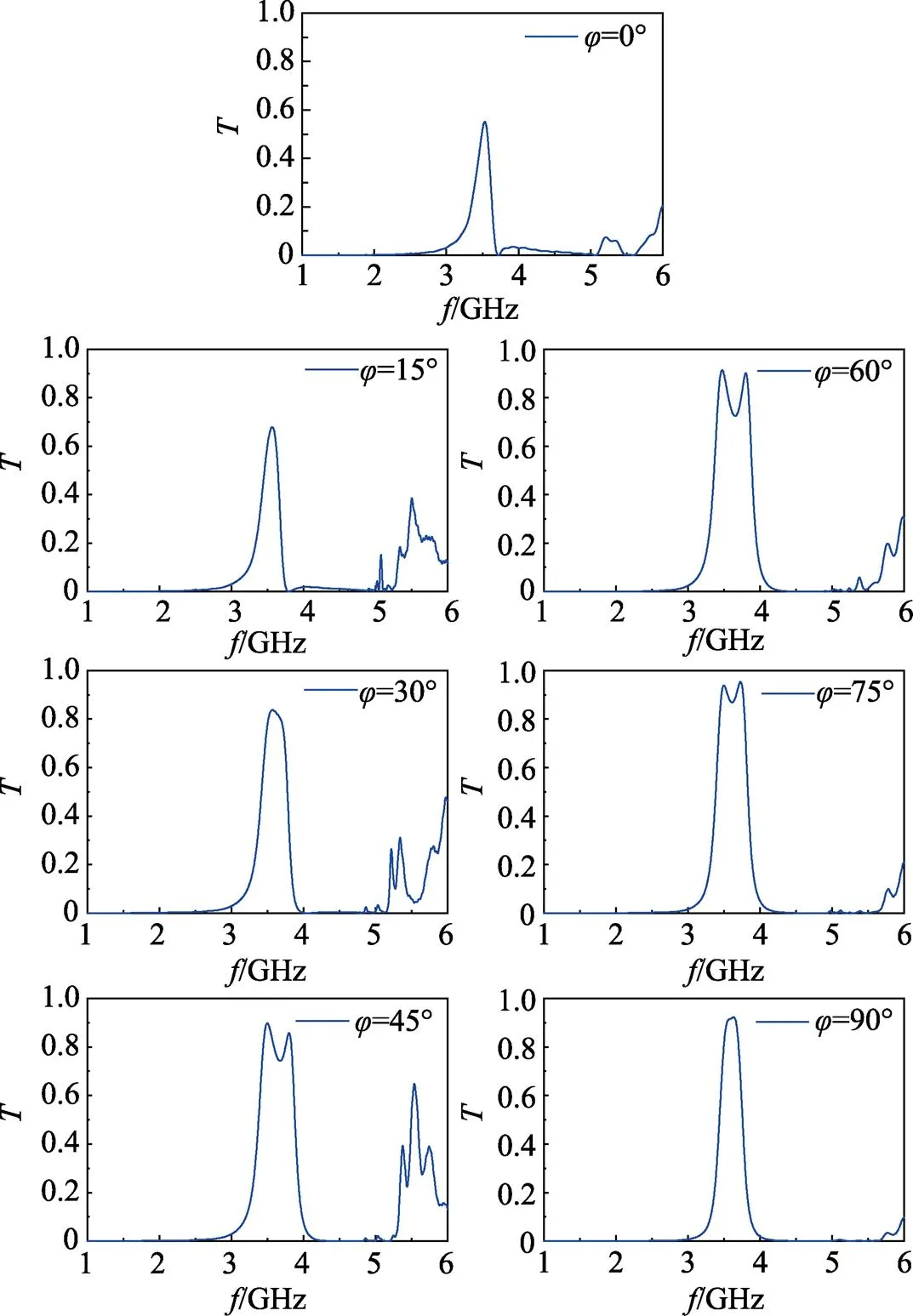
图8 不同偏振旋转的角度下透射系数随频率变化的关系曲线

对于由两个介质偏振片（如：聚乙烯醇片）组成的偏振旋转器，其透射波强度依然满足马吕斯定 律=0cos2，即：透射系数随角的增加而减小。当=0°时，透射效率最高，为1，而当=90°时，透射系数为0。

从图8可以看出，金属偏振旋转器的透射系数不再满足马吕斯定律。这主要是因为在电磁波作用下的两块金属板中的自由电子间的近场耦合作用及电磁波在两层金属板间反复振荡形成的Fabry-Perot干涉效应，这两种效应都有利于电磁波的偏振旋转[8-9]。当=0°时，峰值透射系数较小，只有0.56。随着偏振旋转角度的增大，其峰值透射系数不但不减小反而增大；当=15°时，峰值透射系数为0.69；当=45°时，峰值透射系数为0.89；而当=90°时，其峰值透射系数高达为0.93。显然，双层金属矩形孔阵列的偏振旋转器具有很好的偏振旋转性能。

从图8中还可以看出，随着的增加，透射峰值波长大致不变，在3.49 GHz附近；不过，当为45°、60°和75°时，其透射峰发生了劈裂，从1个透射峰变成了2个峰。

3 结语

本文把科研成果引入到本科教学中，设计的亚波长穿孔金属膜阵列的偏振过滤和偏振旋转实验具有如下优点：偏振片的微结构可见，入射及透射波的偏振方向直观，以及偏振过滤和偏振旋转效应可以定量分析等，弥补了相关专业中偏振相关实验内容的不足。通过本实验的训练，还可以帮助学生了解学科的前沿，对于培养学生的科研兴趣也有一定的帮助。

[1] OZBAY E. Plasmonics: Merging photonics and electronics at nanoscale dimensions[J]. Science, 2006, 311(5758): 189–193.

[2] GENET C, EBBESEN T W. Light in tiny holes[J]. Nature, 2007, 445(2): 39–46.

[3] AMELING R, GIESSEN H. Microcavity plasmonics: Strong coupling of photonic cavities and plasmons[J]. Laser & Photonics Reviews, 2013, 7 (2): 141–162.

[4] EBBESEN T W, LEZEC H J, GHAEMI H F, et al. Extraordinary optical transmission through sub-wavelength hole arrays[J]. Nature, 1998, 391(2): 667–669.

[5] MOLEN K L, KOERKAMP K J K, ENOCH S, et al. Role of shape and localized resonances in extraordinary transmission through periodic arrays of subwavelength holes: Experiment and theory[J]. Physical Review B, 2005, 72 (2): 045421-1-045421-8.

[6] KOERKAMP K J K, ENOCH S, SEGERINK F B, et al. Strong influence of hole shape on extraordinary transmission through periodic arrays of subwavelength holes[J]. Physical Review Letters, 2004, 92(18): 183901-1 -183901-4.

[7] ZHANG Y, LI X K, HUANG C P. High-efficiency wide-band cross-polarization conversion using bi-layered metal hole pairs[J]. Chinese Physics Letters, 2018, 35(10): 104204-1- 104204-5.

[8] ZHANG Y, ZHU J Z, HUANG C P, et al. Wide-band and high-efficiency 90° polarization rotator based on tri-layered perforated metal films[J]. Journal of Lightwave Technology, 2017, 35 (21): 4817–4823.

[9] FAN R H, ZHOU Y, REN X P, et al. Freely tunable broadband polarization rotator for terahertz waves[J]. Advanced Materials, 2015, 27(15), 1201–1206.

[10] DAI M, WAN W W, ZHU X Y, et al. Broadband and wide angle infrared wire-grid polarizer[J]. Optics Express, 2015, 23(12): 15390–1–15390–6.

[11] SUZUKI T, NAGAI M, KISHI Y. Extreme-sensitivity terahertz polarizer inspired by an anisotropic cut-through metamaterial [J]. Optics Letters, 2016, 41(2): 325–327.

[12] HUANG Z, PARROTT E P J, PARK H, et al. High extinction ratio and low transmission loss thin-film terahertz polarizer with a tunable bilayer metal wire-grid structure[J]. Optics Letters 2014, 39(4): 793–796.

Design of polarization experiment based on sub-wavelength rectangular aperture array

ZHANG Yong, LI Xianke, YANG Lan

(School of Physical and Mathematical Sciences, Nanjing Tech University, Nanjing 211816, China)

Based on the research achievements of the surface plasmon theory, a polarizer with sub-wavelength metal rectangular hole array structure is designed. Polarization filtering and polarization rotation effect are realized in microwave band. Polarization filtering effect and Marius law are verified by using polarizers of single-layer metal rectangular hole array, and the polarization rotations of 15°, 30°, 45°, 60°, 75° and 90° are realized by using polarizers of double-layer metal rectangular hole array. This experiment can not only make up for the lack of polarization experiment in science and engineering related courses, but also help students to understand the frontier of the discipline and help them to train and improve their comprehensive scientific ability and quality.

polarization filtering; Marius law; polarization rotation; surface plasmon; microwave band

10.16791/j.cnki.sjg.2019.12.011

O436.3-45

A

1002-4956(2019)12-0044-05

2019-04-08

教育部产学合作协同育人项目（201802355036）；江苏省“大学生创新创业与实践开放基金”项目（201910291089Z）；南京工业大学教育教学改革研究课题（2017113）；南京工业大学“大学生创新创业与实践开放基金”项目（2019DC0809）

张勇（1972—），男，河南信阳，博士，副教授，主要研究方向为表面等离激元光子学。E-mail: yzhang@njtech.edu.cn