高速铁路夕发朝至列车 开行模式组合研究

于 婕，韩宝明，曹金铭

YU Jie, HAN Baoming, CAO Jinming

（北京交通大学 交通运输学院，北京 100044)

(School of Traffic and Transportation， Beijing Jiaotong University， Beijing 100044， China)

自1997年我国铁路第一次大提速提出高速铁路夕发朝至列车以来，全国有大约5 200个高速铁路夕发朝至列车班次。相较于既有线，高速铁路夕发朝至列车由于其快速、舒适、安全等优点受到旅客的青睐。但是，为保障列车开行安全，对线路、信号等设备进行维修的天窗开设，限制了高速铁路夕发朝至列车的运行。铁路相关部门为解决这一问题，对天窗的维修周期进行调整。以北京—广州高速铁路为例，每周二至周四晚0 : 00—6 : 00开设4 h天窗进行维修，每周五至周一安排高速铁路夕发朝至列车开行，不开设天窗，如遇紧急情况，则临时增设小天窗进行维修。铁路部门采取的方法是针对当前的少量客流，大部分现有研究也多针对单一的开行模式，比较不同距离下不同开行模式的优劣。随着经济发展和旅客对于高速铁路夕发朝至列车的认可，客流需求将会不断增加，少列单一开行模式列车将难以满足客流需求。如何在满足客流需求的前提上，以更为合适的开行模式组合确定列车的开行对数，达到更好的开行效果，使铁路综合效益达到最优，实现旅客与运营企业的共赢。

1 高速铁路夕发朝至列车开行模式分析

高速铁路夕发朝至列车的开行模式组合需要从既有研究的天窗开设方式和单一开行模式2个方面进行研究。在天窗的开设方式方面，方华[1]采用分段矩形天窗分析兰新高速铁路开设分段矩形天窗对跨线旅客列车终到时间、通过能力、运行调整等方面的影响；孙玉明等[2]在研究动卧列车时，选择夜间垂直矩形天窗，并从维修作业层面提出强化维修作业的措施和建议；方天滨等[3]认为在上下行列车较为均衡时选择垂直矩形天窗，在不均衡时选择分段垂直矩形天窗。天窗的开设方式多数从矩形天窗入手，分析不同种类的矩形天窗对于开行高速铁路夕发朝至列车的影响以及适应程度。在单线行车模式下，列车风速会对维修工作人员造成很大影响，列车速度被限制在160 km/h以内，电磁设备等的运用也会对人造成危害。因此，研究假设全线开设垂直矩形天窗，在0 : 00—6 : 00间选择4 h作为综合天窗时间。

在列车的开行模式上，赵鹏等[4]以京沪高速铁路(北京南—上海虹桥)为例，提出输送跨线客流的3种开行模式，并就适应旅客需求的适应度进行定义；张天伟等[5]在基于全线矩形天窗的开设方式下分别对列车的等线、下线、下线-上线3种开行模式进行比较分析，并通过建立模型得出不同距离下开行模式的选择；关禹等[6]以沈阳—上海高速铁路为例，从本线的角度研究对高速铁路夕发朝至列车的运行方案展开研究；孙捷萍等[7]基于京广高速铁路，提出4种开行模式，并以旅行时间最佳为目标函数，建模得出优化的高速铁路夕发朝至列车开行方案。

综上分析可以看出，大多数研究主要从单列高速铁路夕发朝至列车入手，优化天窗的开设形式和列车的开行模式。但是，从多列列车的角度出发，需要额外考虑，多列车之间、多列车下线与既有线能力之间的相互影响关系，从而得出贴合实际运营工作的指导建议。因此，在日常化开行高速铁路夕发朝至列车的条件下，研究高速铁路夕发朝至列车在等线、下线、下线-上线3种开行模式下列车的开行对数，考虑旅客的始发终到满意度、时间惩罚成本和调度指挥组织难度3方面因素，建立列车开行模式组合优化模型。

（1）等线模式如图1所示，图中的阴影部分表示垂直矩形天窗，列车在车站m进行等待后继续运行。

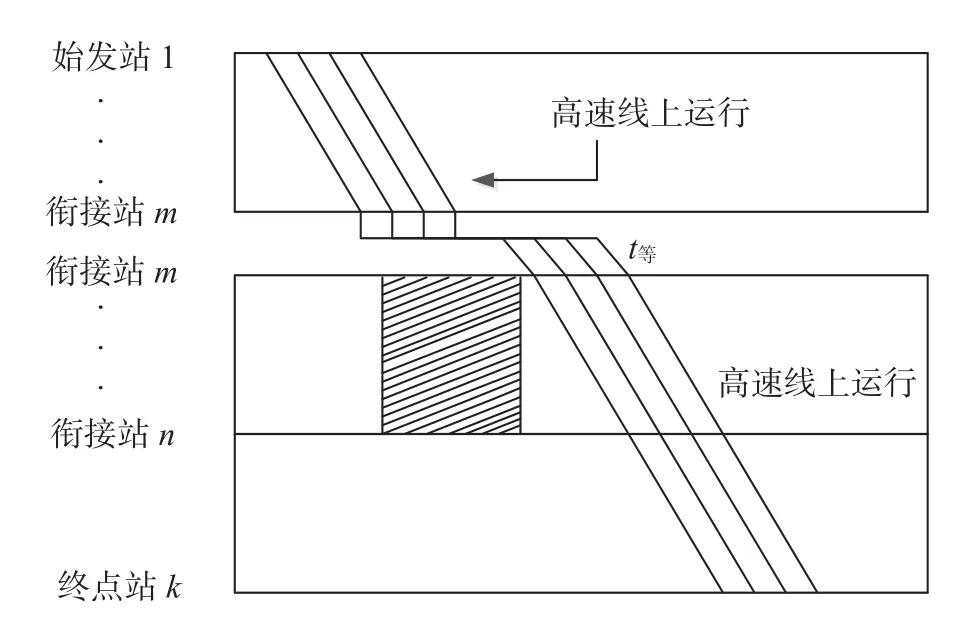
图1 等线模式Fig.1 Parallel track mode

（2）下线模式如图2所示，高速铁路夕发朝至列车在衔接站进行转线，消耗t下线无效，虚线表示列车从车站m到既有线运行至终点站k。对于衔接站和区间m至k，假设都满足行车条件及安全运行的线路条件。

图2 下线模式Fig.2 Mode of running on the existing railway line

（3）下线-上线模式如图3所示，虚线表示列车在既有线运行，跨过天窗时间，实线表示在高速线上运行，前3列车符合下线-上线的开行模式。

图3 下线-上线模式Fig.3 Mode of conventional line-high speed line oepration

2 高速铁路夕发朝至列车开行模式组合优化模型

2.1 模型假设

假设高速铁路夕发朝至列车始发时间为18 : 00—24 : 00，终到时间为6 : 00—11 : 00，全程运行7 ～ 15 h。但实际运行中由于列车晚点，故障等突发情况的发生，使得问题研究过于复杂。为简化研究，在建立模型时做出以下假设。

（1）铁路线路一切完好，没有设备故障等突发事件发生，列车均正点运行，不存在晚点现象。

（2）列车在转线过程中不考虑车站没有联络线等情况，均假设每个车站有充足的联络线且既有线路的设备均适合高速铁路夕发朝至列车开行。

（3）列车上下线途中，在联络线、到发线等线路运行时所产生的时间假设均等。

（4）假设停站时间均包含在列车的运行时分中。

（5）求解时，认为下线和下线-上线高速铁路夕发朝至列车为理想状态下的连发方式，常见的3种列车运行图的铺画方式如图4所示。可以看出3种铺画方式中，集中铺画方式下的车流密度最小，其通过能力最大。

图4 常见的3种列车运行图的铺画方式Fig.4 Three common ways in which the train diagram is laid out

2.2 0-1 变量

列车在运行过程中，途径区段e1，e2，…，em，…，ek，k= 1，2，…，K，K＞ 2，各区段距离为d1，d2，…，dm，…，dk，分别表示区段e1，e2，…，em，…，ek之间的距离。设i= 1，2，3分别表示等线，下线，下线-上线开行模式，j= 1，2，3，4，5，6表示在高速铁路上的速度类型为vk,1= 350 km/h，vk,2= 300 km/h，vk,3= 250 km/h，以及在既有线上的速度类型为vk,4= 160 km/h，vk,5= 140 km/h，vk,6=120 km/h。根据铁路实际情况，目前高速铁路夕发朝至列车车型均为D字头，最高速度不超过250 km/h，在既有线上运行时为最高级别的运行速度，因而选取j= 3，4。

4个0-1变量含义如表1所示，其中关键地点指列车选择下既有线或上高速线运行的车站。

表1 0-1变量含义Tab.1 0-1 variable meaning

2.3 约束条件

（1）0-1变量的约束条件。由实际可知，一列列车在开行时有且只能选择一种开行模式，即

公式 ⑵ 至公式 ⑷ 用来判断列车在哪种线路上运行。

公式 ⑸ 至公式 ⑹ 表示速度为 250 km/h 的列车在高速线上运行，速度为160 km/h的列车在既有线上运行。

对于等线模式和下线模式，只需选择1个关键地点，而对于下线-上线，则需要2个关键地点，由此得出以下逻辑关系。

（2）列车运行约束条件。

①到发线数量约束。列车在采用等线模式运行时，列车等待必须占用客运站的到发线，因而客运站必须预留出相应数量的线供列车等待，约束条件为式中：Dk表示k站的到发线数量。

②关键地点选择约束。对于第2种和第3种开行模式关键地点的选择，当列车下既有线运行时，选择离天窗时间最接近的车站下线，出行时间最短，因而满足以下约束条件

式中：tm表示列车行驶至关键车站时刻；表示天窗开始时刻；dm,m+1表示2个车站之间的距离；vk,3表示第3种运行速度。

当列车由既有线上线至高速铁路时，需要考虑以下约束。

公式 ⑾ 表示列车在选择关键地点上高速线运行时，如果大于在下一站点上线在既有线的运行时间，列车选择第n+ 1个车站作为关键车站；公式⑿ 则表示如果在该站点的等待天窗的上线时间小于在下一站点上线在既有线的运行时间，列车选择在第n个车站选择等待上线。

2.4 目标函数

研究认为，旅客的始发终到出行满意度影响着旅客的出行行为，对客流需求造成一定的影响；将时间惩罚成本简化为高速铁路夕发朝至列车对既有线通过能力影响，与调度指挥难度2种因素影响着运输产品供给、铁路公司的运营成本等。这3种因素是是高速铁路夕发朝至列车对铁路综合效益贡献值的重要组成因素。

（1）旅客的始发终到出行满意度是一种主观心理状态，难以量化，仅能通过发放调查问卷了解。通过李洁等[8]对不同运行时长的列车始发时刻和终到时刻对于旅客出行的影响研究，借用问卷调查得出的不同始发终到时间段的偏好程度图表，选取部分数据进行拟合，得出[19 : 00—24 : 00]和[6 : 00—10 : 00]的曲线和公式。旅客不同出发时段偏好程度如图5所示，旅客不同到达时段偏好程度如图6所示。

在图5和图6中，红点表示调查数据，实线为软件拟合曲线，可以发现，2条曲线更符合高斯分布，因而得出以下公式。

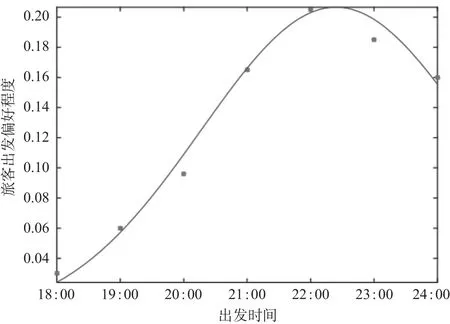
图5 旅客不同出发时段偏好程度Fig.5 Preference degree of passengers at different departure time

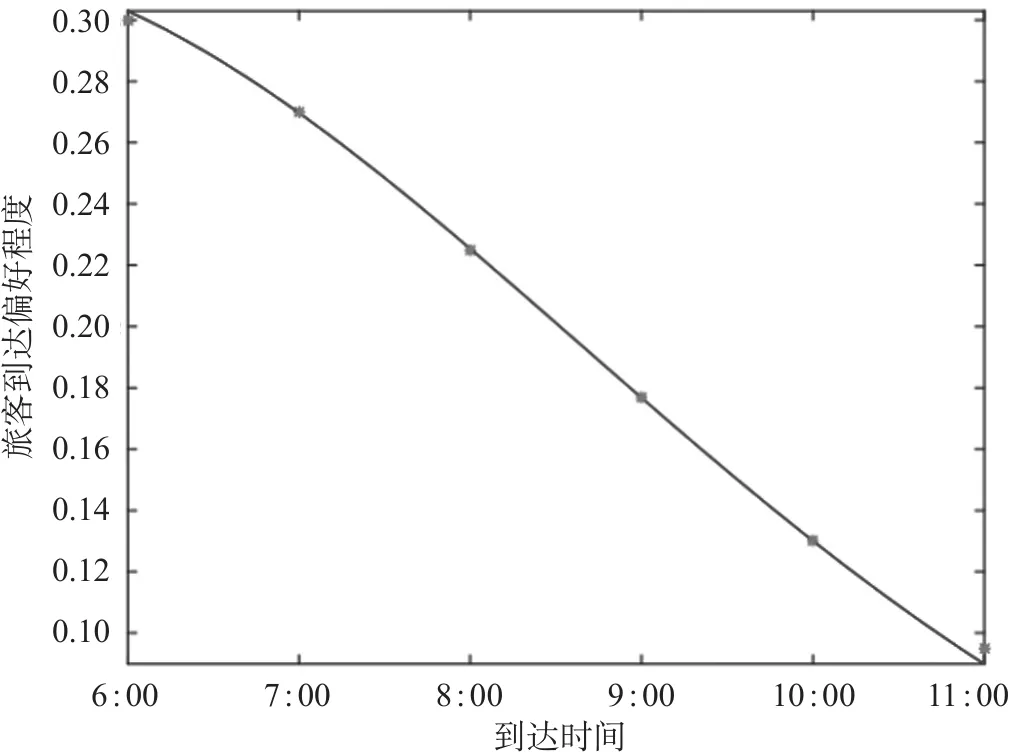
图6 旅客不同到达时段偏好程度Fig.6 Preference degree of passengers at different arrival time

始发时刻偏好程度计算公式为

式中：ω表示时间；f1(ω)表示对始发时间段的偏好程度值。

终到时刻偏好程度计算公式为

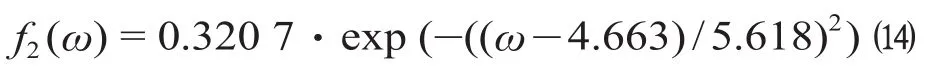
式中：f2(ω)表示对终到时刻的偏好程度值。

公式 ⒀ 和 ⒁ 的置信度均为 95% 。

（2）时间惩罚成本。随着高速铁路通过能力的饱和，越来越多的高速列车选择下既有线运行，以满足旅客的出行需求。但是，越行既有线的客货列车，不仅影响列车的速度指标，也造成既有线通过能力的损失，因而应探讨不同的列车开行模式对既有线通过能力的影响。通过引入惩罚系数λ，对越行既有线客货列车所造成的时间消耗成本进行计算，简化对既有线通过能力影响的计算。计算过程中，等线列车在等待天窗时在车站某一存车线上等待，其对高速铁路区段通过能力的影响可以忽略，主要考虑下线和下线-上线列车。时间惩罚演示图如图7所示。

图7 时间惩罚演示图Fig.7 Illustration of time penalty

式中：λ表示惩罚系数，为连发的所有下线和下线-上线高速铁路夕发朝至列车对一列既有线列车的总影响时间与该车平均运行时间t既平均的比值；t1为一列下线高速铁路夕发朝至列车使既有线列车待避所花费的总等待时间；t2为一列下线-上线列车使既有线列车待避所花费的总等待时间；x为下线列车数量；y为下线-上线列车数量。

式中：M表示下线和下线-上线高速铁路夕发朝至列车对既有线造成的时间惩罚成本；α为既有线列车为完成运输任务所产生的单位时间消耗成本；t既平均发车间隔表示既有线列车的平均运行间隔；为受影响列车列数。

（3）调度指挥组织难度。在开行跨线列车时，由于线路与设备条件的差异，使运输组织和调度指挥难度增加，而第2个因素时间惩罚成本已包含运输组织所产生的影响。因此，仅对不同开行模式的调度指挥难度系数设置权重[9]如下，等线、下线、下线-上线3种开行模式的调度指挥难度依次增加。

求解过程中，对3个因素进行量纲归一化处理，具体处理公式为

式中：min (x)为归一化数组x中的最小值；max (x)为归一化数组x中的最大值。

在归一化处理过程中，t既平均发车间隔，t既平均，α都被消掉，因而不作具体数值的查找，3种函数分别由Z1，Z2，Z3表示。则目标函数可变为

式中：Z表示归一化之后铁路的综合效益；“+”表示对铁路的正面收益；“-”表示对铁路的负面收益；Z1表示旅客始发终到满意度函数值；Z2表示对既有线通过能力的影响函数值；Z3表示运输组织难度函数值。对公式进一步拆解，Z1中，始发时间偏好值f arrive和终到时间偏好值f departure应各占1/2；Z2，Z3的自变量值分别为时间惩罚成本M和调度指挥难度函数f；i表示3种开行模式，l表示列车的开行数量，xi,l为0-1变量，表示第l列车的第i种模式，则表示不同开行模式列车的开行数量之和；L表示计划最大开行列车数量。时间惩罚成本是所有跨线列车对既有线列车的影响，而旅客的平均始发终到满意度调度指挥平均组织难度Z3(f)为一列跨线列车的数值，乘以开行数量，表示所有跨线列车的满意度和调度组织难度。

2.5 模型求解

研究选用遗传算法进行求解。通过对基本遗传算法进行调整，选择便于大空间搜索且精度高的实数编码方式对问题进行编码操作。由于列车开行方式需要求解，但首列列车出发时间与天窗开始时间不确定，这2个因素会对结果产生影响，故需要设计特定的染色体结构进行求解，染色体编码如图8所示。其中，第一位基因td1表示第一列车的发车时间；最后一位基因tstc为天窗开始时间，中间i为列车的开行状态，取值为1，2，3，分别表示等线、下线、下线-上线，i的数量即为列车的数量。

图8 染色体编码图Fig.8 Coding diagram of chromosomes

本算法中适应度函数为目标函数，为避免适应度函数为负影响选择算子运算，对适应度函数进行处理，增加常数c，在这里c取1。

遗传算法流程如图9所示。

3 实例应用

以京广高速铁路(北京西—广州南)及其平行既有线为例，京广高速铁路北起北京西站，南至广州南站，全长2 298 km，共设37个车站，设计最高速度350 km/h，运营速度为300 km/h，满足下既有线条件的车站有石家庄站、郑州东站、武汉站和长沙站。京广高速铁路车站布置情况如图10所示，京广既有线车站布置情况如图11所示。

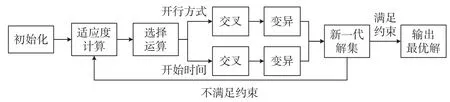
图9 遗传算法流程Fig.9 Fow of genetic algorithms

图10 京广高速铁路车站布置情况Fig.10 Station layout of Beijing-Guangzhou high-speed railway

图11 京广既有线车站布置情况Fig.11 Station layout of Beijing-Guangzhou existing railway line

其遗传算法参数设置如表2所示。算法中参数取值如下：初始种群大小为100，交叉概率为0.6，变异概率为0.01，最大迭代次数为500。计算中t下线无效= 20；t上线无效= 20；t1= 5；t2= 10。

表2 遗传算法参数设置Tab.2 Parameter setting of genetic algorithm

为求解和验证列车开行模式组合优化模型，分别从开行1列车至开行10列车进行模型求解，每次实验使用遗传算法求解10次，每次保留最优结果，既有等线开行模式与列车开行模式组合比较如表3所示，同时计算出当前高速铁路夕发朝至列车全部等线开行模式下的函数值，将二者进行比较。

结果图如图12所示。图12可以看出，最大适应度在260代达到1.552 3后，趋于稳定，因而认为最大迭代数500可以满足优化目标的要求，且算法收敛性较好。

既有等线开行模式与列车开行模式组合比较，选择开行1 ～ 5列车时，列车均选择等线开行，根据既有研究求解结果[6]，北京至广州的超长距离列车选择等线运行，从侧面验证其模型的可靠性；开行6 ～ 10列车时均出现下线列车，说明随着开行列车数量的增加，单一等线模式已经不是模型的最优结果。由表3可以看出，列车开行模式组合优化模型的目标函数要比全部采用等线开行模式更高，特别在开行10列列车时，有8列选择下线运行，这是由于等线列车在线路上等线导致旅客到达时间满意程度明显下降所导致。因此，随着客流量的增加，仅靠现有的等线模式，不仅不能满足客流需求，也不符合铁路的综合效益。随着既有线和高速铁路线路调度指挥体系的不断完善和协同发展，组织难度将逐渐降低，选择优势增加。因此，在未来夕发朝至客流量增加时，列车开行模式组合的选择要比全部等线开行更符合铁路的综合效益。

表3 既有等线开行模式与列车开行模式组合比较Tab.3 Comparison of the existing parallel track running mode and train operation mode combination

4 结束语

通过对多列高速铁路夕发朝至列车开行模式组合问题进行研究，少量高速铁路夕发朝至列车开行等线模式最优，而随着列车数目的增加，在最优模式组合中，下线模式的列车比例逐渐增加，突破了以往的研究。由于高速铁路夕发朝至列车的开行列数直接影响到列车选择的开行模式，在未来高速铁路夕发朝至列车开行数量增加的情况下，还应考虑列车运行距离开行模式组合的影响程度，加强不同运行距离下开行不同数量列车最优开行模式组合方案的研究。

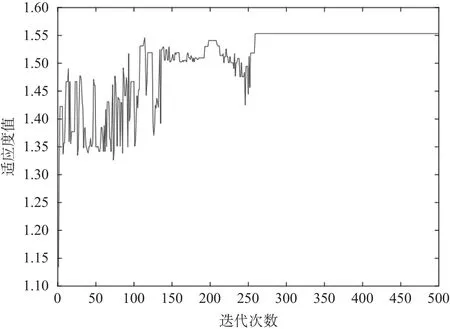
图12 结果图Fig.12 Graphical results