基于单目视觉与里程计的组合室内定位研究*

方章云，袁 亮，侯爱萍，吴金强

(新疆大学 a.机械工程学院；b.纺织与服装学院,乌鲁木齐 830047)

0 引言

伴随着移动机器人定位技术的快速发展，基于传感器的同时定位与地图构建[1](Simultaneous Localization and Mapping, SLAM)技术成为研究的热点。用于SLAM技术的常见传感器有相机、激光雷达、IMU(惯性测量单元)、里程计等。而VSLAM[2](Visual SALM)技术主要优点是采用相机作为单一的外部感知传感器。J Engle等[3]于2015年提出的LSD-SLAM是利用基于像素的直接法进行SLAM工作，但是光照变化对其影响大，且计算成本高。而2017年Mur-Artal等基于原有的ORB-SLAM[4]提出了ORB-SLAM2[5]，该方法以单目视觉为主，整个过程均采用ORB特征点，极大的缩短了计算时间，然而单目ORB-SLAM2无法提供尺度信息，只能提供带有比例缩放的轨迹，因此许多学者将目光转向多传感器融合，其中Mur-Artal等使用单目ORB-SLAM与IMU的结合十分突出[6]，将IMU提供的惯性数据用于紧耦合融合，插入预积分作为约束，进而实现对单目ORB-SLAM跟踪的改进，但是IMU的初始化依赖于SLAM。周绍磊等[7]利用INS与ORB-SLAM结合实现了室外的惯性导航，利用精度为5cm的差分GPS估计尺度因子，有效的提高了定位精度，该方法成本较高，且GPS不适合在室内实现移动机器人的定位。王泽华等[8]添加磁力计改进IMU的姿态解算实现与SLAM的松耦合，该方法通过IMU位姿信息估计相机的尺度因子，而IMU的位姿信息是通过加速度的二重积分计算得到，因此加速度的微小测量噪声会被放大，从而影响到移动机器人的定位。

综上所述，单目相机作为SLAM所用的传感器，成本较低，使用方便，缺点是无法提供真实深度信息。本文采用ORB-SLAM2算法，利用全向移动机器人里程计估算尺度因子，并将ORB-SLAM2输出的经尺度变换后的位姿信息和里程计位姿进行卡尔曼滤波，最终根据误差比重加权实现对移动机器人的定位。

1 移动机器人算法模型描述

1.1 全向移动机器人航迹推算算法

本文采用的是三轮全向移动机器人[9],而传统的室内移动机器人采取的是两轮差速的小车底盘，机械结构具有很强的约束性，很难实现在室内拥挤环境下的小半径转弯，因此全向移动机器人在室内狭窄环境下沿任意方向移动更有优势。

对于全向移动机器人，假设机器人坐标系和世界坐标系的初始夹角为θ，x轴方向上的速度为vx，y轴方向上的速度为vy，自转的速度为ω，各轮子中心到机器人中心的距离为L=0.43m且是中心对称分布，由此可以得到全向移动机器人3个轮子的速度为：

(1)

其中，V1、V2、V3分别为3个轮的转速。

为方便计算取θ=0，即求解出vx、vy、ω：

(2)

本文采用的全向移动机器人DR算法是从二轮差速底盘改进而来，根据原有的二轮差速DR算法[10]，选择固定其中一轮方向与机器人坐标系(y-o-x)y轴重合，假设全向移动机器人的偏航角范围为-180°～180°(顺时针为正)，如图1所示移动机器人从tn时刻到tn+1时刻，全向轮底盘的偏航角变化为Δθ=θ2-θ1以及在tn时刻机器人坐标系下y轴方向的速度为vy，x轴方向的速度为vx。

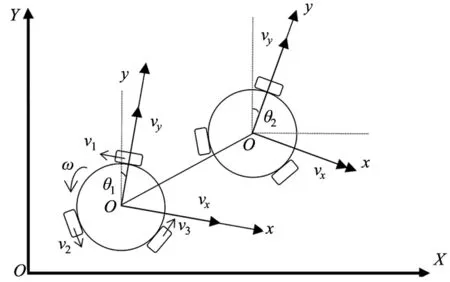
图1 三轮全向移动机器人DR算法模型

当编码器采样时间足够短时，此时x、y轴上的速度变化不明显，因此可以将vx、vy分别正交分解到世界坐标系Y-O-X可得：

将vy、vy分别分解到X，Y轴上：

(3)

其中，vyY、vyX为速度vy分别在世界坐标系Y、X上的投影，vxY、vxX为速度vx分别在世界坐标系Y、X上的投影。

因此可以得到全向轮底盘里程递推公式为：

(4)

其中，Y、X分别为全向移动机器人在世界坐标系X、Y方向上的坐标，θ为航向角，下标n为任意时刻。

1.2 单目视觉ORB-SLAM2算法

单目ORB-SLAM2[5]算法是基于旋转不变性的ORB特征实现，算法创新式地使用了三个线程并行完成SLAM工作：首先利用Tracking线程实时跟踪特征点，并用局部Bundle Adjustment最小化重投影误差，进而进行定位构图，在算法运行过程中利用视觉字典进行回环检测，在检测到回环之后会对相机位姿进行全局BA，从而大大提高定位精度。

在使用ORB-SLAM2之前需要对单目相机进行标定，得到相机内参参数fx、fy、cx、cy以及畸变系数，填写相应的参数文件。然而，单目视觉SLAM算法在通过SVD分解本质矩阵求解旋转矩阵R和平移矩阵t时，会存在尺度等价性问题，而R∈SO(3)自身具有约束，但t和本质矩阵分解的奇异值有关，所以不同的t决定了空间三维点的深度，换言之，单目ORB-SLAM2中，对轨迹和地图同时放缩任意倍数，得到的轨迹形状依然是一样的。因此，本文利用全向移动机器人里程计来实现单目视觉尺度因子的估计。

2 DR/ORB-SLAM2融合算法

2.1 尺度因子估计

融合算法流程如图2所示，本文通过卡尔曼滤波对底盘位姿和ORB-SLAM2经尺度转换后的位姿进行过滤噪声，通过误差比重进行松耦合加权实现对机器人的定位。其中全向移动机器人的里程计算经过码盘的平均采样和PID调速较传统里程计累计误差小，因此能利用全向移动机器人的里程位姿作为估计单目ORB-SLAM2尺度因子的信息。

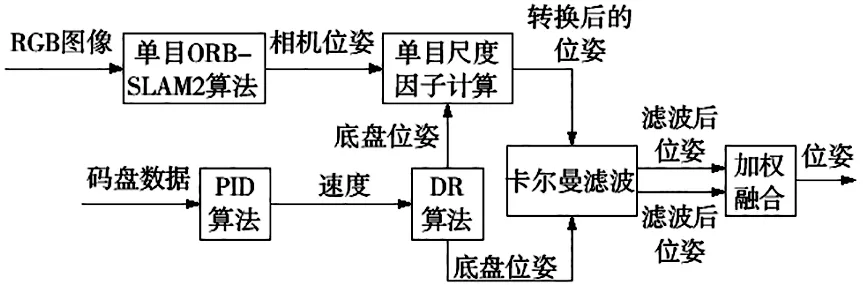
图2 融合算法流程图

ei=bi-sR·ai-b0(i=1,2,…,n)

(5)

其中，ei为第i次的测量误差，R和b0分别为相机坐标系到机器人坐标系的旋转矩阵和平移向量，s为单目ORB-SLAM2的尺度因子。

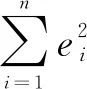
(6)

函数Q对s求偏导并令其为0得：

(7)

在单目初始化后，全向移动机器人移动的短距离内分别取n个时刻相机位置和对应的n个里程计位置。而函数的极值点即是所求的尺度因子s。如图3所示，分别求取X、Y方向的尺度值，随着点数的增加最终同时趋向于s=3.4182。

图3 X、Y方向尺度因子估计

2.2 数据融合

由于DR和单目ORB-SLAM2输出的经尺度变换的位姿轨迹存在噪声，轨迹不光滑，因此利用卡尔曼滤波分别对两组轨迹进行滤波得到位姿Xa、Xb。

构建目标数学模型：

运动模型：Xk=AXk-1+εk

(8)

观测模型：Zk=CXk+δk

(9)

在获得较为平稳的数据后，再通过位置均方根误差权值的比重进行加权融合。见式(10)：

(10)

其中,w1、w2分别为ORB-SLAM2经尺度转换后的位置和DR的位置均方根误差，X为融合后位姿。

3 实验结果及分析

如图4所示，实验的硬件采用的是三轮全向移动机器人底盘，控制层采用的是STM32F103系列开发板，同时采用增量式PID算法实现对底盘三个电机的精准控制；上层采用联想Y410P系列的PC机作为机载计算机，通过ROS机器人操作系统实现对多个传感器的话题信息提取，并利用rosbag包记录话题信息。视觉传感器采用型号为XGY300，像素为300万的单目相机，激光雷达采用测距分辨率为0.5mm的Rplidar A2。具体实验平台如图5所示。

图4 硬件系统图

图5 全向移动机器人实物图

实验在6m×5m的室内范围内进行，地面为普通的光滑平面，全向移动机器人只在平面上移动，相当于只在XY平面上移动，在Z轴上只有转动，故取全向移动机器人的运动轨迹以及航向角作为实验对比数据，同时利用rosbag记录的时间，将里程计、激光雷达、ORB-SLAM2算法输出的数据按照每秒的间隔求和平均对齐，保证数据的一致性。由于实验场景较大，人工量取移动机器人真实轨迹较困难，因此采用Rplidar A2实现的Hector SLAM[11]算法绘制的轨迹作为真实轨迹进行对比，如图6所示。

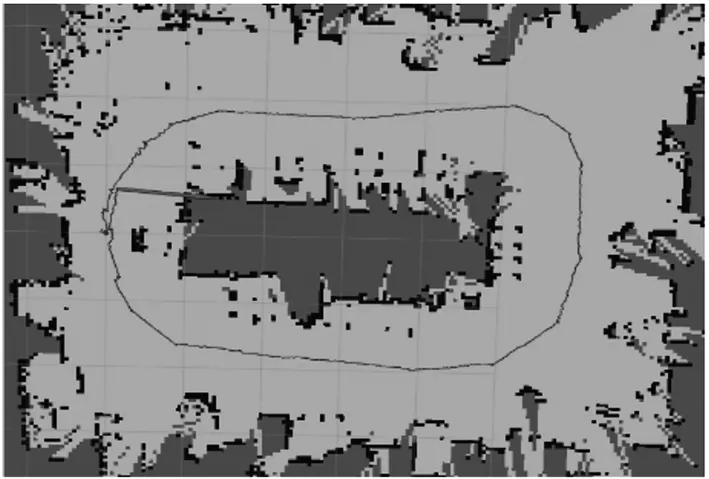
图6 实验场景地图

图7为不同算法对机器人定位的轨迹点,在实验中，移动机器人由于抖动会使轨迹不光滑，以及单目相机、激光雷达、里程计坐标起点没有实现完全对齐等都会使轨迹数据产生偏差，在本文使用的算法中，ORB-SLAM2是带有回环检测的，因此融合ORB-SLAM2后的轨迹图也会带有回环的特性，能大大减小定位误差。

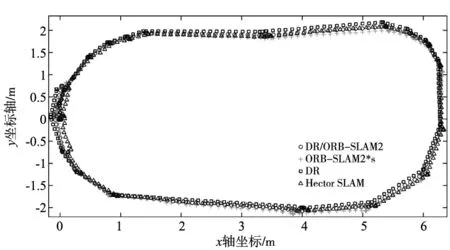
图7 轨迹对比图

机器人的制造误差以及单目相机的标定误差等均会造成不同程度的定位误差，因此在X、Y方向上的定位误差都会略有不同，如图8、图9所示，由于移动机器人在X、Y方向上的运动距离的不同，运动距离较短的Y方向的误差较小，同时可以发现，虽然移动机器人的定位误差处于波动状态，但大多数位置的误差均能保持在0.1m以内。其中本文方法在X、Y方向上的误差均方根为0.0761m、0.0293m，均小于原算法。

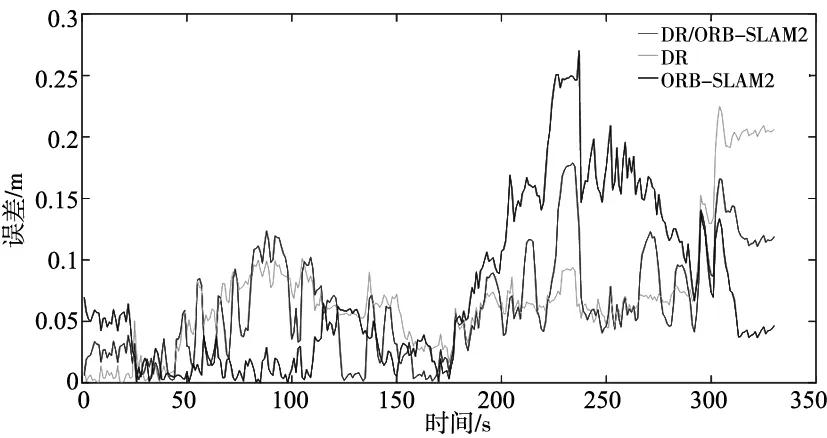
图8 X方向误差

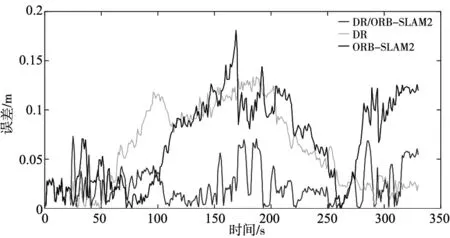
图9 Y方向误差

在移动机器人定位中，往往还需考虑机器人的朝向问题，即航向角，如图10所示，可以观察到航向角的变化是符合运动航向变化的，4条曲线基本保持一致，本文方法的航向角误差大小始终保持在7°以内。

图10 航向角对比图

本文的方法最终数据对比结果如表1所示。

表1 各项数据均方根误差对比

由表中的实验数据可以看出,融合后的轨迹位置相对原来的DR和ORB-SLAM*s的位置结果分别提高了27.85%、36.60%，而航向角上的误差比ORB-SLAM*s大，但相对于DR提高了30.83%。

4 结束语

本文采用DR算法与单目ORB-SLAM2结合，为单目ORB-SLAM2算法提供了尺度因子估计方法，以及通过卡尔曼滤波与比重加权实现对里程计位姿以及经尺度变换后输出的ORB-SLAM2位姿融合。实验结果表明，本文方法使移动机器人在定位结果上相对于原来的里程计和单目视觉定位结果分别提高了27.85%、36.60%。然而，算法仍有不足，在单目尺度因子估计上，由于运动时间过长后，里程计的DR误差会产生累计，不能很好的实现对里程计数据点的选取。下一步可以考虑将里程计与单目视觉进行紧耦合融合，保证尺度因子估计的稳定性。

DOI:10.1109/TRO.2016.2624754.