基于模糊人工势场法的机械臂避障达点研究
韩 峰,赵 京
(北京工业大学 机械工程与应用电子技术学院,北京 100124)
0 引言
机器人的路径规划算法有RRT,A*等,还有一些人工智能算法。但是人工势场法以其简单的特点获得了广泛的应用。人工势场法是由KHABIT[1]提出的。王俊龙等[2]利用虚拟斥力势场法解决了人工势场法中的局部极小问题。唐彪等[3]利用添加虚拟目标点来改进人工势场法。Wei Guan等[4]利用变步长结合重构的势场函数来逃离局部极小点。杨小菊等[5]利用模糊控制算法进行移动机器人的避障研究,将传感器采集到的信息反馈给模糊控制器,进而不断修正位姿进行避障。Amal Karray等[6]利用自适应模糊控制器实现移动机械臂的轨迹追踪和避障。
针对人工势场法常见的局部极小问题的解决方法大多集中在陷入极小问题后如何逃离,本文通过添加模糊控制器控制引力与斥力势场权重系数可以避免陷入局部极小,规避该问题。
1 人工势场法的原理
传统的人工势场法就是在笛卡尔空间中引入了引力势场以及斥力势场,引力势场是由目标点对机械臂的吸引产生的,而斥力势场是由障碍物对机械臂的排斥所产生的。在这两个合势场的共同作用下,机械臂到达目标点并实现了避障。设机械臂的当前位置是P=[x,y,z],目标点的位置是Pg=[xg,yg,zg],那么引力势场的一般式如式(1)所示。
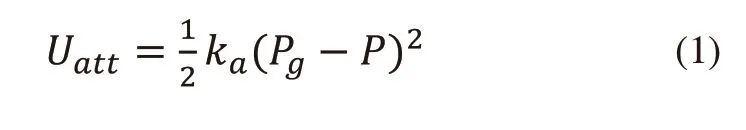
式(1)中ka表示引力势场系数,Uatt就是引力势场。
斥力势场表示为式(2)所示。

式(2)中kr是斥力场系数,ρ(P0,P)是障碍物到机器人的距离,ρ0是斥力势场的影响距离,是一个常数。
2 改进算法
2.1 关节空间搜索
传统的人工势场法通常针对的是平面移动机器人,在二维空间中受引力和斥力的合力作用。但这里是针对机械臂的路径规划,而机械臂是强耦合以及在三维空间运动的。如果在三维空间进行路径规划就需要进行反解,这就大大增加了计算量,同时容易出现奇异点的问题。本文中是在关节空间进行的规划。关节空间搜索方法如下:
1)设当前的关节位置为θ=(θ1,θ2,…,θn),n为机械臂关节数目。
2)设定步长为σ,遍历每个关节角的相邻位置,每个关节角都有3个位置,则总共有3n种组合方式。
在手术室内,由经管护士继续以亲切的语言和热情的态度与其交流,与患者建立良好的护患关系,以减轻其因为环境改变而带来的心理压力。给患者介绍手术环境,手术过程,以及注意情况,多与患者沟通,适时给予安慰和鼓励,及时解决患者的心理问题,提高患者对其自身疾病的认知程度和应对能力。消除患者对手术疼痛的恐惧感及焦躁的情绪,以积极平和的心态应对术后疼痛等问题,提高对治疗的依从性。
3)计算每种组合的合势能,最小的势能所对应的关节角就是下一步的关节角位置。
4)如此循环计算,直至到达目标点。
在关节空间中搜索,将合势场作为目标函数,机械臂就向着合势场最小的方向运动,该方式规避了反解等问题。降低了计算的难度和强度。
2.2 势场函数
针对人工势场法中势场函数中的参数引力与斥力势场系数ka,kr不好确定的问题,这里对势场函数进行了改进,确定了参数的选取。
引力势能:

式(3)中P是机械臂末端的位置,Pg是目标点位置,Pc是机械臂末端初始位置。
斥力势能:

3 模糊控制器设计
这里设计了一个模糊控制器来控制势场函数中的引力势场权重系数Wa和斥力势场权重系数Wr。该模糊控制器将机械臂与障碍物的距离以及该距离的变化率作为输入,权重系数Wa,Wr作为输出。如图1所示。

图1 势场权重模糊控制器
引入权重系数后,合势场就如式(5)所示。根据机械臂与障碍物的距离以及距离变化率,模糊控制器控制两权重系数的大小。

输入为障碍物与机械臂距离,其论域是[100,1000],其模糊语言变量为['VN','N','M','F','VF'],距离变化率的论域为[-1,1],模糊语言变量为['Negative','Zero','Positive']。图2为机械臂与障碍物距离隶属度函数,这里用的是三角形隶属函数。图3为机械臂与障碍物距离变化率隶属度函数。

图2 障碍物距离隶属度函数
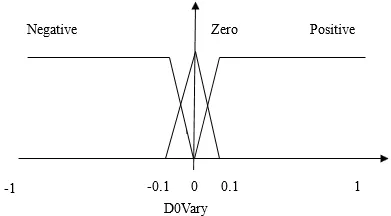
图3 障碍物距离变化率隶属度函数
输出为引力势场权重系数Wa和斥力势场权重系数Wr。Wa其论域为[5,1 0],模糊语言变量为['VS','S','M','B','VB'];Wr论域为[0,5],模糊语言变量为['VS','S','M','B','VB']。图4和图5分别为Wa和Wr的隶属度函数。模糊系统的Wa和Wr输出曲面如图6、图7所示。

图4 引力势场权重系数隶属度函数

图5 斥力势场权重系数隶属度函数
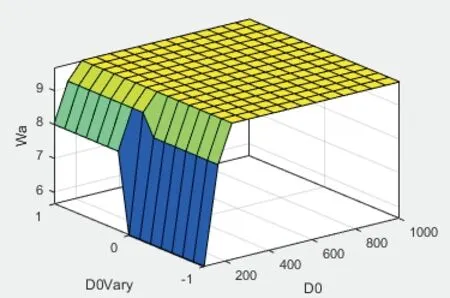
图6 引力势场权重系数输出曲面

图7 斥力势场权重系数输出曲面
该模糊控制器的规则如表1所示。本文的模糊推理采用Mamdani法,反模糊化采用了重心法。采用的是IFTHEN条件语言,共有3×5=15条模糊控制规则。

表1 模糊控制规则
4 仿真实验
4.1 机械臂建模
这里用MATLAB进行了仿真实验。选定的机械臂为kukaiiwa机械臂,如图8所示。其DH参数如表2所示。这里仿真只用到该机械臂的前四个关节。

图8 kukaiiwa机械臂

表2 kukaiiwaDH参数
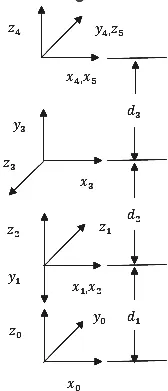
图9 机械臂前四个自由度DH参数模型
该kukaiiwa机械臂是七由度的,有肩部,肘部和腕部。这里只关注前四个自由度,腕部关节作为末端点。

式(6)、式(7),式(8)中P,Pe,Ps分别是机械臂末端,肘部以及肩部的空间位置坐标。
4.2 局部极小问题
假设机械臂初始位置时θ=[0,0,0,0,0,0,0],目标点的坐标为Pg=[400,400,400],障碍物坐标为P0=[200,200,500],d0min=100,d0max=300。首先对传统算法的进行了仿真。图10是传统算法中机械臂的四个关节角位置图。

图10 传统算法机械臂四个关节角位置
由图可以看出机械臂关节角保持不变,机械臂末端并为达到目标点。此时机械臂陷入了局部极小。同样的任务对改进算法进行了仿真。关节角位置如图11所示。

图11 改进算法机械臂四个关节角位置
图12是机械臂末端与目标点距离,由图可以看出机械臂到达了目标点。机械臂与障碍物距离如图13所示,可以看出机械臂与障碍物距离大于最小安全阈值d0min,机械臂实现了避障达点。
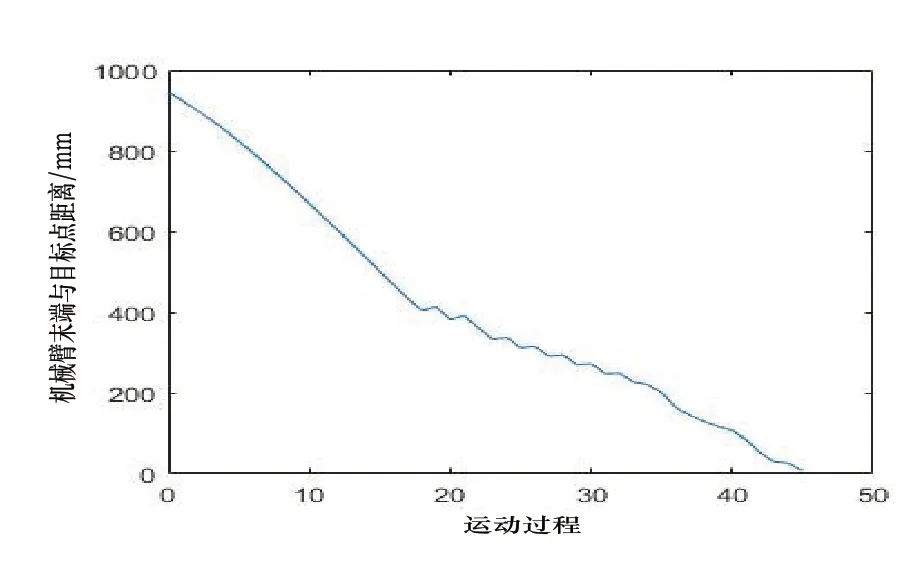
图12 机械臂末端与目标点距离

图13 机械臂与障碍物距离
5 物理样机实验
这里使用了kukaiiwa机械臂进行了实验验证。如图14所示,机械臂实现了避障达点运动。

图14 kukaiiwa机械臂避障实验
6 结语
使用模糊人工势场法在关节空间进行避障路径规划,对原算法的势场函数进行了改进,同时加入了权重系数,利用模糊控制器控制该参数,解决了局部极小问题。通过MATLAB仿真以及kukaiiwa机械臂的实验验证了方法的有效性。

