某O 型密封圈的双参数加速退化规律分析

王莉，顾晓辉，潘守华

（1. 南京理工大学，南京 210094；2. 北方特种能源集团西安庆华公司，西安 710025）

橡胶密封圈是一种常用的密封元件，具有高弹性、压缩变形大和能承受重复载荷等优点[1]，使用范围广，应用价值高。由于橡胶材料自身分子结构的特点，使其在使用和贮存过程中会受到许多因素的影响，从而逐渐老化，最终丧失使用价值。因此，橡胶密封圈是产品的薄弱环节，对其退化规律进行分析可以预测其寿命，从而给产品的维修和替换提供理论依据。

获取橡胶材料寿命数据的方法有自然贮存试验和加速寿命试验。前者能得到最精确的数据，却受限于试验周期太长、试验成本过高等因素，较少使用；后者则是通过提高橡胶所受的应力（如温度应力）来加速其老化过程，试验成本和时间得到控制，目前使用较为广泛。根据加速寿命试验获得的数据进行寿命评估的方法主要是动力学曲线直线化法[2]，该方法通过建立橡胶材料性能与试验时间之间的方程以及加速方程，对实际情况下橡胶材料的寿命进行预测。

目前对橡胶材料老化的研究主要是对单一性能参数进行观测，但退化过程中往往存在多个性能参数。多参数影响下橡胶材料的寿命与依据单参数评估得到的寿命会有一定差距。因此，文中以永久压缩变形率和压缩应力松弛率为参数，对某O 型密封圈进行恒定应力加速退化试验，分析其退化规律并对其寿命进行可靠性评估。

1 加速退化试验原理

恒定应力加速退化试验是利用恒定的高应力来加快产品退化的试验方法，根据试验获得的性能退化数据可以预测和估计产品在实际环境下的可靠性及性能保持时间[3]。试验的前提条件是产品在不同的应力条件下失效机理保持不变，即退化机理存在一致性[4]，同时在加速过程存在加速模型。

橡胶在贮存过程中，会受到环境中热能、光能、机械能和辐射能的作用，同时还会和空气中的成分发生化学反应，破坏自身结构，出现老化变形的现象，失去使用价值。橡胶密封件在贮存条件下老化的机理主要是热氧老化和机械应力下的橡胶蠕变[5]。在热氧老化期间，由于受热，橡胶密封圈分子链发生降解和交联反应。降解反应导致分子链断裂从而材料变软、发黏并丧失机械强度，交联反应则使材料变脆和失去弹性从而失去密封性能[6]。加速退化试验中常依据热氧老化机理选择温度应力作为加速应力。

加速模型描述了加速试验中寿命特征与应力水平之间的关系，它的建立是进行外推的基础，会直接影响外推的精度。当加速应力为温度时，常用的加速模型为阿伦尼斯模型[7]。结合退化数据与试验时间之间的关系、加速模型和使用条件，可以预测橡胶密封圈的寿命。

2 试验

2.1 方案

试验对象为某O 型密封圈，材料是硫化丁腈橡胶，属于轴向安装的静密封元件。该密封圈的尺寸为φ3.5 mm× 25 mm。选择对性能影响最大的温度应力作为加速应力，丁腈橡胶的使用温度范围为-30～130 ℃。选择设置4 个温度应力水平：50、60、70、80 ℃，每个温度应力水平下投入8 个样品，样本总数为32。

丁腈橡胶性能退化的主要表现为变脆、变硬和弹性消失，将性能参数定为压缩永久变形率ε 和压缩应力松弛率δ。考虑到橡胶材料在低温环境中会物理收缩[8]，在设定失效阈值时，要补偿低温收缩量。低温环境下，当ε＞31%或者δ＜80%时，会发生泄漏。将ε =31%、δ =80%定为O 型密封圈的失效阈值。

文献[9]表明，试验中进行6 次检测可以得到较好的橡胶材料性能退化拟合曲线。本试验也进行6 次检测，随着试验温度的升高，相邻检测次数的时间间隔要相应地缩短。检测时间的安排见表1。

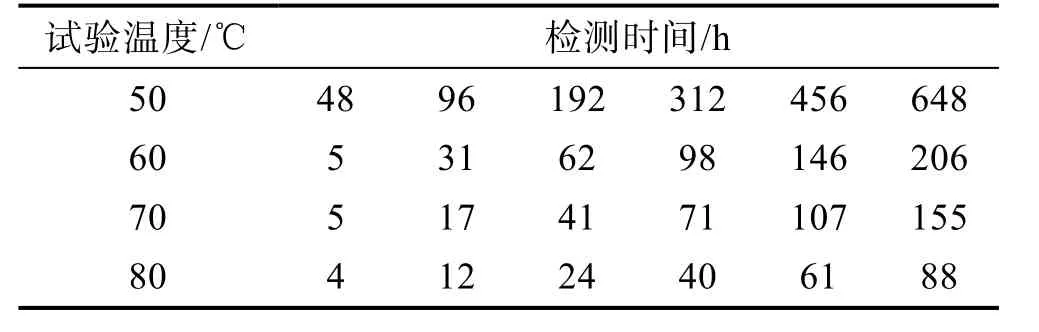
表1 各试验温度的检测时间安排

实际使用中，O 型圈被轴向安装以承受轴向压力。为模拟实际安装状态，设计了模拟夹具。该夹具采用LC4 硬铝材料，由上下2 块夹板、限高环以及4枚螺栓构成，如图1 所示。限高环的高度是样品初始轴向高度的70%，从而使O 型圈在夹具内保持30%的压缩率。

图1 模拟夹具实物

2.2 试验步骤

试验中所需设备有：恒温试验箱（XMTD-9000），温控精度为1 ℃；橡胶测厚仪（CH-12.7-ATSX），测量精度为0.01 mm；数显式推拉力计（HP-100），测量精度为0.1 N。

从同一批O 型圈产品中选出32 个样品，分成4组，将样品安装在模拟夹具内。为获得样品试验前的性能参数初始值，将夹具在室温中放置1 天进行预压，再取出样品静置1 天，等待其恢复。随机在O型圈的两面各取均匀分布的4 个点，用测厚仪测量它们的厚度，取其均值作为样品轴向厚度的初始值。同样，用推拉力计测量O 型圈上8 个分布点的弹性压力，取其均值作为压力的初始值。

给恒温箱设定试验温度，将一组样品置于其中，按照表1 安排的检测时间点取出样品，在室温下冷却1 h，按上述方法测得轴向厚度和弹性压力两组数据。当一组样品检测结束后，给恒温箱重设温度，并投入一组新的样品，继续测量和记录数据，直至4 组试验完成。

3 退化规律分析

3.1 试验数据处理

试验结束后，得到O 型圈的轴向厚度与弹性压力两组数据。压缩永久变形率的计算公式为：

式中：ε 为压缩永久变形率，%；D0为样品试验前测得的轴向厚度初始值，mm；Dx为夹具的限制高度，mm；Dt为样品在检测时刻t 测得的轴向厚度，mm。

压缩应力松弛率按式（2）计算：

式中：δ 为压缩应力松弛率，%；σt为样品在检测时刻t 测得的弹性压力值，N；σ0为试验前样品测得的弹性压力初始值，N。

根据式（1）和式（2）分别计算各样品在检测时间点的压缩永久变形率和压缩应力松弛率，由此得到永久变形率曲线和应力松弛率曲线，如图2 和图3所示。

3.2 退化轨迹方程

橡胶材料的老化过程可以用老化动力学方程表示：

式中：P 为橡胶残余性能；B 为试验常数；K 为老化速度常数，与温度相关；t 为老化时间；α 为时间指数，0＜α＜1。

对于压缩永久变形参数，P=1-ε，表示O 型圈在t 时间后残留的压缩永久变形率，代入到老化动力学方程，得：

对式（4）两端取对数，得：

图2 压缩永久变形曲线

图3 压缩应力松弛率曲线

采用逐次逼近法对参数α1进行估算，即确定使残差平方和I1最小时α1的取值，I1的表达式为：

式中： Y1ijk是根据检测数据计算得到的实际值；是根据α1的取值对式（6）进行拟合得到的估计值。

经计算，α1=0.32 时，Imin=0.1108。确定了参数α1后，对式（6）进行线性回归分析，估算式（4）中各参数的值，得到各样品的退化轨迹方程，共32 个。此处仅列出50 ℃下1 号样品的退化方程：

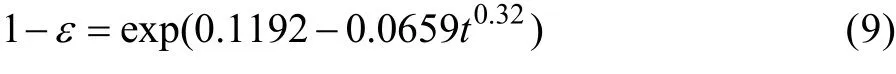
对于压缩应力松弛参数，可用上述方法得到各样品的退化轨迹方程。其中，P=δ，表示O 型圈在t 时间后残留的压缩应力松弛率，代入式（3）得：

令 Y2=ln(1 - ε)， X2=， a2= ln B2， b2=- K2，建立一元线性回归方程：

经计算，α1=0.12。50 ℃下1 号样品的退化方程为：

退化轨迹方程中，拟合参数的具体数值见表2。

3.3 伪失效寿命分布

将失效阈值ε=31%、δ=80%代入到各样品的退化轨迹方程中，得到各样品的伪失效寿命，具体数据见表3。

正态分布可用于分析由于老化而发生失效的产品[10]。采用Wilk-Shapiro 的W 检验法检验各样品的伪失效寿命，检验统计量W 的值见表4。

根据检验统计量W 的分位数表，当显著水平取0.05，样本容量为8 时，W0.05=0.818。与表4 中的计算值进行比较，可以得出结论：各试验温度下样品的伪失效寿命均服从正态分布。利用最小二乘法得到伪失效寿命分布的参数即均值μ 和标准差σ 的估计值，见表5。

表2 退化轨迹方程中的拟合参数值

表3 各样品的伪失效寿命

表4 W 检验的计算值

表5 各样品伪失效寿命分布的参数估计值

对表5 中μ 和σ 的估计值进行最小二乘回归分析，得到相关系数r1=0.9897，r2=0.9416，两者均大于相关系数临界值（2=0.9），即线性回归效果显著。因此可以认为各试验温度下伪失效寿命的均值与标准差的比值相等，即在加速退化试验中，O 型圈的加速失效机理具有一致性[11]。

3.4 加速寿命方程

加速方程描述了产品的寿命特征与应力之间的关系，本试验的试验条件为热应力，因此根据阿伦尼斯模型建立加速方程，见式（13）。

式中：K 为老化速度常数；A 为正常数；E 为激活能，与材料有关；R 为玻尔兹曼常数；T 是绝对温度。

对式（13）两端取对数，得：

相关系数依次为0.9981、0.9506、0.9917、0.9833，根据相关系数临界值表，r0.05=0.95。由于各参数的相关系数均大于0.95，因此加速方程的线性回归效果显著。

3.5 可靠性分析

产品的寿命服从正态分布时，其可靠度函数表示为：

则可靠寿命为：

依据式（15）—（18）列出的加速方程，得到20 ℃对应的均值μ 和标准差σ，代入式（20），得到在温度为20 ℃和可靠度为0.9 时O 型圈的寿命评估结果：根据压缩永久变形数据得到的结果为8.695 年，根据压缩应力松弛数据得到的结果为8.748 年。

假设压缩永久变形和压缩应力松弛两个参数相互独立，则双参数的可靠度函数为单参数可靠度的乘积：

单个参数的可靠度曲线与双参数的可靠度曲线如图4 所示。可以看出，双参数不相关时的可靠度小于单个参数的可靠度。可靠度为0.9 时，双参数不相关情况下的寿命评估结果为8.655 年。

图4 可靠度函数曲线

4 结论

以压缩永久变形和压缩应力松弛为参数，以温度应力作为试验应力，对某O 型密封圈进行了加速退化试验，并对退化数据进行处理，分析其老化规律，得出以下结论。

1）某O 型密封圈的寿命服从正态分布，其性能退化具有可加速性，可以使用加速退化试验的方法分析其老化规律。

2）基于压缩永久变形参数和基于压缩应力松弛参数得到的评估结果较为接近，验证了本次试验及数据处理方法的有效性。

3）假设两个性能参数之间相互独立，考虑双参数综合影响时的寿命评估结果会比单参数情况下小。