火箭末级的天线布局建模与优化

刘宇哲，张 群，杨 勇，张新宇，彭慧莲

(北京宇航系统工程研究所，北京100076)

1 引言

随着我国航天事业的快速发展，在轨航天器数量越来越多，充分利用燃料消耗殆尽的航天器(如上面级或者火箭的末子级等)正成为一种有效节约成本的方案[1-2]。但在航天器燃料耗尽后，航天器起旋并保持绕本体的匀速自转过程中，各电气系统须工作正常，天线信号通联时长得到保障。

航天器上的天线信号覆盖范围一般是空间圆形锥体，最大不超过一个半球[3]。当航天器起旋并保持绕本体的匀速自转且在航天器本体可见范围内存在测控通信站时，天线所形成的圆锥体信号覆盖范围将不断扫略地面测控站，从而建立通信链路。在航天器保持匀速自转的约束条件下，为了增加通信链路建立的时间，有效的处理办法有2种：一种是尽可能多地增加天线数量，使得天线圆锥体信号收发范围能够完全覆盖整个航天器本体的球体包络[4]，这种方式是粗放的，且极大地消耗了航天器上有限的能源；另一种方式是通过优化天线布局，尽可能减少天线布局数量，同时能够达到建立通信链路的有效时长要求[5]。本文采取第二种方式保证建立通信链路的时长。

目前关于航天器上天线的研究主要集中于天线的定位机构的指向精度方面和卫星点波束覆盖区域方面的研究[6-8]，鲜有关于星载天线布局的研究内容发表。而关于天线布局的研究，更多的则是关于固定姿态下的车载、舰载和机载的天线布局优化研究[9-11]。本文利用其他行业的天线布局优化技术，应用于定轴旋转姿态下航天器的天线布局优化。将航天器简化为一个含有姿态信息的位点，天线信号辐射范围简化为一个空间圆形锥体，通过建立天线布局姿态与航天器本体的空间相对位置关系和地面测控站与航天器本体的空间相对位置关系，映射得到天线布局姿态与信号覆盖测控站的时长关系模型；再通过数值仿真得到3种不同布置角度下天线覆盖各测控站时长的图谱，并以覆盖时长最长为目标函数，利用遗传算法对布置3个天线的航天器进行优化，以得到3个天线能够覆盖最广范围的布局形式。

2 天线信号覆盖范围建模

本文的研究对象是一个以定角速度绕本体Z轴旋转的航天器，如图1所示，本体上安装有数个固定于本体的天线。考虑以航天器本体作为基坐标系，测控站是围绕航天器本体的Z轴以定角速度旋转的，因此可以将等Z轴面上的测控站集合到图中X-Z平面上的红色位点。只要在图中X-Z平面上能够被天线信号覆盖到的红色位点，则位于该等轴面上的测控站均能在航天器自转过程中被天线信号覆盖到，区别只是时间的长短。由于航天器本体是匀速自转的，因此信号覆盖时间的长短是由等轴面信号覆盖范围的弧长决定的。

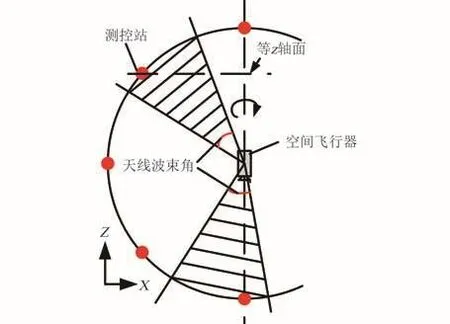
图1 天线信号覆盖范围的模型Fig.1 Model of signal radiation range

通过以上分析可知，3种安装角度的天线对应3种不同的建模形式，因此本节建立3种状态的天线信号覆盖范围模型，分别称为0°俯仰角模型、正向俯仰角模型和负向俯仰角模型。

2.1 0°俯仰角模型

空间中天线以锥形扫略地面测控站的X-Z向视图如图2所示，O代表天线(即航天器本体)所在的位置，天线绕Z轴旋转一周，会扫过地面某一测控站TA，αA表示天线的单向张角，即天线最大张角为2αA。地面测控站位于X轴夹角为θA的位点TA。天线信号在X-Z平面覆盖的范围为SA1SA2围成的弧段，SA为天线信号覆盖范围的中线位置。由TA向Z轴作垂线，与SA1SA2的交点为QA，对应的等Z轴面的圆半径为rA1。由于天线信号覆盖范围只和角度有关，因此可以假定天线所在空间的球形为半径为1的单位球。0°俯仰角模型表示天线信号覆盖范围的中线位置SA位于X轴上，即SAz＝0。

根据式(1)所示球坐标定义：

以及图2中的几何关系，由式(2)～式(5)可以获得基于姿态信息αA的位点数据SA1x、SA1z、SA2x和SA2z：

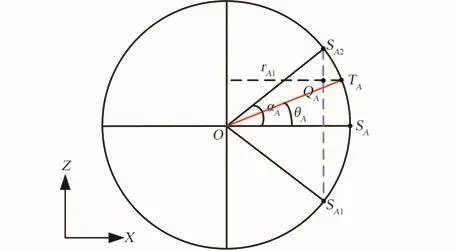
图2 0°俯仰角的天线信号覆盖范围在X-Z向的投影Fig.2 The 0°pitch angle model of signal radiation range in X-Z plane projection

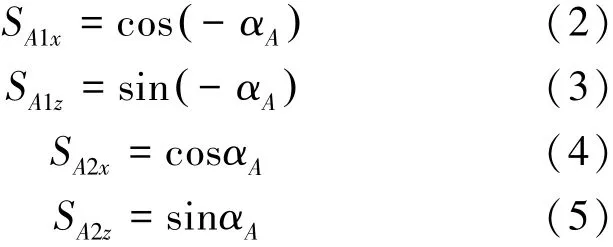
根据图2中的几何关系和SA1x、TAz数据，由式(6)和式(7)可以获得QAx和QAz：

由图3所示，TA与QA的位置是相互关联的，并进一步结合图4可知，在天线旋转扫描过程中，TA将与QA1或者QA2重合，因此可知天线扫描地面测控站的距离或者时间由QA1QA2的弧长决定，其平面示意图可见图5。而QA1QA2的弧长由QA1QA2的距离lA所决定，QA1QA2的距离则是其Y向的距离，式(8)～式(12)构建了由QA1和QA2两个位点的x和z轴数据求解其对应y轴数据以及距离lA：

天线扫描测控站的夹角如式(13)所示：

其中，vA表示OQA1的向量，eA表示X轴的单位方向向量。QA1QA2的弧长所对应的圆的半径为式(14)：

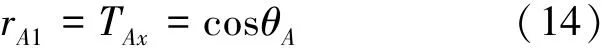
图3 天线信号覆盖范围的二维视图Fig.3 Signal radiation range in 2D view

图4 天线信号覆盖范围的三维视图Fig.4 Signal radiation range in 3D view

图5 0°俯仰角的天线信号覆盖范围在X-Y向的投影Fig.5 The 0°pitch angle model of signal radiation range in X-Y plane projection

则基于QA1QA2的距离lA和所对应的圆半径rA1即可确定天线信号覆盖地面测控站的弧长，也就可以进一步得到天线信号覆盖地面测控站的时长。

2.2 正向俯仰角模型

空间中天线以锥形扫略地面测控站的X-Z向视图如图6所示，O代表天线(即航天器本体)所在的位置，天线绕Z轴旋转一周，会扫过地面测控站TB，αB表示天线的单向张角，即天线最大张角为2αB。地面测控站位于X轴夹角为θB的位点TB。天线信号在X-Z平面覆盖的范围为SB1SB2围成的弧段，SB为天线信号覆盖范围的中线位置，OSB与X轴的夹角为φB。由TB向Z轴作垂线，与SB1SB2的交点为QB，对应的等Z轴面的圆半径为rB1。正向俯仰角模型表示天线信号覆盖范围的中线位置SB位于圆形的上半部，即SBz＞0。

图6 正向俯仰角的天线信号覆盖范围在X-Z向的投影Fig.6 Positive pitch angle model of signal radiation range in X-Z plane projection

根据式(15)所示球坐标定义：

根据图6中的几何关系，由式(16)～式(19)可以获得基于姿态信息αB的位点数据SB1x、SB1z、SB2x和SB2z：

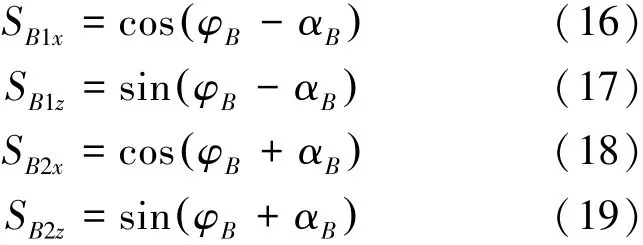
求取基于SB1和SB2的直线方程系数如式(20)～(21)：

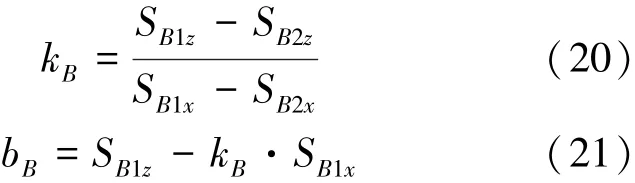
根据图6中的几何关系，由式(22)可以获得坐标值QBz：

根据直线方程则由式(23)可以求得坐标值QBx：

由于TB与QB的位置是相互关联的，在天线旋转扫描过程中，TB将与QB1或者QB2重合，因此可知天线扫描地面设备的距离或者时间由QB1QB2的弧长决定，如其平面示意图 7。而QB1QB2的弧长由QB1QB2的距离lB所决定，QB1QB2的距离则是式(24)～(26)所示QB1QB2的Y向距离：

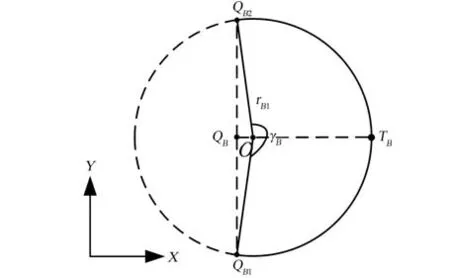
图7 正向俯仰角的天线信号覆盖范围在X-Y向的投影Fig.7 Positive pitch angle model of signal radiation range in X-Y plane projection

天线信号覆盖测控站的夹角为式(27)：

其中，vB表示OQB1的向量，eB表示X轴的单位方向向量。

如图8所示，当天线的接收范围在＋Z向覆盖较广时，位于＋Z向的地面测控站将会全天候接收到天线的信号，此时对应的数理判定条件为QBz＞SB2z；类似地，当天线的接收范围在-Z向覆盖较广时，位于-Z向的地面测控站将不会接收到天线的信号，此时对应的数理判定条件为QBz＜SB1z。

图8 正向俯仰角的特殊情况Fig.8 Special situation of positive pitch angle model

2.3 负向俯仰角模型

空间中天线以锥形扫略地面测控站的X-Z向视图如图9所示，O代表天线(即航天器本体)所在的位置，天线绕Z轴旋转一周，会扫过地面测控站TC，αC表示天线的单向张角，即天线最大张角为2αC。地面测控站位于X轴夹角为θC的位点TC。天线信号在X-Z平面覆盖的范围为SC1SC2围成的弧段，SC为天线信号覆盖范围的中线位置，OSC与X轴的夹角为φC。由TC向Z轴作垂线，与SB1SB2的交点为QC，对应的等Z轴面的圆半径为rC1。负向俯仰角模型表示天线信号覆盖范围的中线位置SC位于圆形的下半部，即SCz＜0。

图9 负向俯仰角的天线信号覆盖范围在X-Z向的投影Fig.9 Negative pitch angle model of signal radiation range in X-Z plane projection

根据式(28)所示球坐标定义：

根据图9中的几何关系，由式(29)～式(32)可以获得基于姿态信息αC的位点数据SC1x、SC1z、SC2x和SC2z：

求取基于SC1和SC2的直线方程系数如式(33)～(34)所示：

根据图9中的几何关系，由式(35)可以获得坐标值QCz：

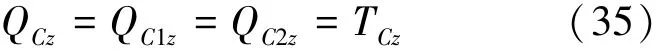
根据直线方程则由式(36)可以求得坐标值QCx：

由于TC与QC的位置是相互关联的，在天线旋转扫描过程中，TC将与QC1或者QC2重合，因此天线扫描地面测控站的距离或者时间由QC1QC2的弧长决定，平面示意见图 10。而QC1QC2的弧长由QC1QC2的距离lC所决定，QC1QC2的距离则是如式(37)～(39)所示的QC1QC2的Y向距离：

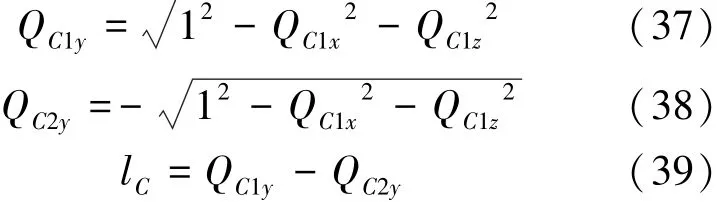
图10 负向俯仰角的天线信号覆盖范围在X-Y向的投影Fig.10 Negative pitch angle model of signal radiation range in X-Y plane projection

天线信号覆盖地面测控站的夹角如式(40)所示：

其中vC表示OQC1向量，eC表示X轴的单位方向向量。

如图11所示，当天线的接收范围在＋Z向覆盖较广时，位于＋Z向的地面接收站将不会接收到天线的信号，此时对应的数理判定条件为QCz＞SC2z；类似地，当天线的接收范围在-Z向覆盖较广时，位于-Z向的地面测控站将全天候接收到天线的信号，此时对应的数理判定条件为QCz＜SC1z。

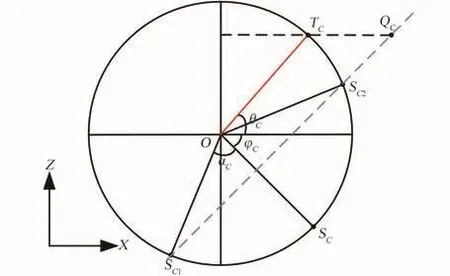
图11 负向俯仰角的特殊情况Fig.11 Special situation of negative pitch angle model

3 模型优化

将遗传算法应用到天线信号覆盖范围的优化问题中，对影响覆盖范围的关键参数进行优化。

3.1 优化目标

由建模分析可知，影响天线覆盖范围的因素为天线的波束角张角α和天线安装的俯仰角φ。同时考虑三维空间中天线信号的重复覆盖问题，还需考察在X-Y平面上天线安装的偏摆角β。偏摆角β表示在X-Y平面上，天线信号覆盖弧长在等Z轴面圆弧上的移动角度。因此，天线信号覆盖范围扫过第i个测控站的弧长角度区间(ψ1，ψ2)i可以表示为式(41)所示波束角张角α、天线安装的俯仰角φ和偏摆角β的函数：

由于航天器以匀速绕Z轴自转，所以可以用天线信号覆盖范围扫过的弧长对应的角度来替代表达天线信号覆盖范围扫过的时长。

在X-Z平面均布n个测控站，则可以观测若干天线信号能够覆盖的总角度ψ如式(42)所示：

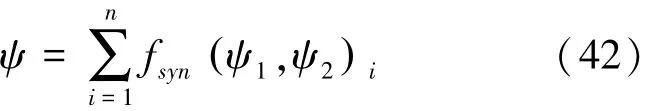
其中，函数fsyn的作用在于将位于同一个测控站下的3个天线的覆盖范围进行综合统计。

天线全天候完全覆盖n个测控站的全部角度集合S可以表达为式(43)：

则评价天线信号覆盖比率的指标η可以表达为式(44)：

3.2 优化参数和边界

影响天线覆盖范围的关键参数为α、φ和β，α表示天线张角，是天线的固有属性，因此一般是固定的。因此真正影响天线信号覆盖范围的参数是天线的布局安装角度：俯仰角φ和偏摆角β，因此本文对3个天线的6个俯仰角和偏摆角参数进行优化。为了减少优化数据计算量，且根据基本的天线布局规律，可以将优化布局的3个天线的关键参数进行优化区域划分，设定天线A的安装角度优化域为φA＝0°，βA∈[-90°，90°]；天线B的安装角度优化域为φB∈[0°，90°]，βB∈[0°，180°]；天线C的安装角度优化域为φC∈[-90°，0°]，βC∈[-180°，0°]，即3种优化域分别对应着0°俯仰角模型，正向俯仰角模型和负向俯仰角模型。由于在0°俯仰角模型中φA＝0°，因此实际优化5个天线布局的关键参数。

3.3 算法参数

遗传算法参见文献[12]，本文中涉及的遗传算法参数如见表1所示，包括种群规模M、个体基因长度L、进化次数(即迭代次数)G，交叉率Pc和变异率Pm。种群规模M代表在每一次进化(迭代)中，有M个优化参数组合参与到进化中；个体基因长度L代表每个被编辑的基因的长度，本文涉及五个优化参数，则每一个优化参数由L/5长度的基因信息表达；进化次数G表达的是进化次数，多次迭代后，最优结果稳定，即可认为进化次数是足够的；交叉率Pc代表的是基因以Pc的概率被选择出来进行交叉操作；变异率Pm代表的是基因以Pm的概率被选择出来进行变异操作。一般来说这个参数会小一些，因为变异不知道会使得个体会变优还是会变差，但是一定的基因变异率可以加快找到最优解。

表1 遗传算法参数Table 1 Parameters of genetic algorithm

4 仿真及结果

4.1 仿真验证

基于以上建立的天线信号覆盖范围模型和优化模型，在MATLAB中建立相应的仿真程序。仿真算例中，天线的张角设定为120°，即单向张角α为60°，设定图谱中横坐标表示地面测控站的分布角度θ为[90°， 80°， 70°， 60°， 50°， 40°， 30°， 20°，10°， 0°， -10°， -20°， -30°， -40°， -50°， -60°， -70°， -80°， -90°]；图谱中纵坐标表示天线信号覆盖范围(即代表信号通联的时长)。仿真中设定基于0°俯仰角模型的天线安装角φA＝0°，βA＝0°；基于正向俯仰角模型的天线安装角φB＝20°，βB＝30°；基于负向俯仰角模型的天线安装角φC＝-20°，βC＝-30°，则可以得到典型安装布局状态下，3种天线的信号覆盖范围谱图，如图12～14所示。

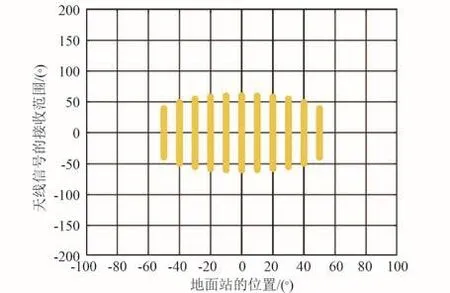
图12 基于0°俯仰角模型的仿真Fig.12 Simulation based on 0°pitch angle model

图14 基于负向俯仰角模型的仿真Fig.14 Simulation based on negative pitch angle model

仿真结果显示，基于0°俯仰角模型的天线覆盖范围更多地集中在图谱的中心位置区域，并大致呈现椭圆形状；基于正向俯仰角模型的天线覆盖范围主要集中在图谱的右侧，并有部分位置测控站的信号通联时长是完全覆盖的，即航天器任意旋转姿态下都能获得通联信号；基于负向俯仰角模型的天线覆盖范围主要集中在图谱的左侧，并有部分位置测控站的信号通联时长是完全覆盖的，即航天器任意旋转姿态下都能获得通联信号。仿真结果表明，该结果与实际状态一致，验证了模型和仿真程序的有效性。

4.2 优化计算

本文设定19个均布的测控站，将天线信号覆盖比率的指标η的最大值作为优化目标，即在本体可见范围内天线的信号覆盖比率。遗传算法的优化过程可见图15，可以看到大概在进化160次后，种群中的个体无论怎么进化，最优结果已经不再变化了，此时可以认为找到了最优解。

图15 遗传算法的优化过程Fig.15 Optimization process of genetic algorithm

最优解对应的天线布局角度的参数为βA＝1.23°，φB＝65.36°，βB＝178.30°，φC＝-65.36°，βC＝-176.04°， 其对应的η＝83.98%，覆盖范围图谱如图16所示。优化结果显示，优化后的天线布局方案除了在图谱的中上和中下部存在类三角形区域接收不到信号外，其他地方均能获得良好的通联时长。相较于经验布局参数βA＝0°，φB＝45°，βB＝135°，φC＝-45°，βC＝-135°，其对应的η＝79.85%，提高了4.13%。

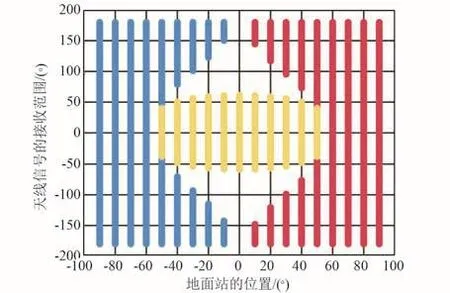
图16 优化后的三个天线信号覆盖范围Fig.16 Signal radiation range of three antennas after optimization

5 结论

1)基于理论模型的数值仿真计算显示，基于0°俯仰角模型的天线覆盖范围更多地集中在图谱的中心位置区域，并大致呈现椭圆形状；基于正向俯仰角模型的天线覆盖范围主要集中在图谱的右侧；基于负向俯仰角模型的天线覆盖范围主要集中在图谱的左侧。

2)以3个天线信号覆盖范围最广为优化目标，利用遗传算法，优化得到了最优解对应的天线布局角度 的 参 数 为βA＝ 1.23°，φB＝ 65.36°，βB＝178.30°，φC＝-65.36°，βC＝-176.04°，其对应的天线信号覆盖比率η＝83.98%，优化后的天线布局方案除了在图谱的中上和中下部存在类三角形区域接收不到信号外，其他区域均能获得良好的通联信号。

3)本文的优化方法可避免传统的根据经验布局天线并计算验证的方法的盲目性和局限性，为天线布局提供了理论基础，提高了论证布局方案的效率，也可对更多或更少数量的天线进行布局仿真和优化。