大功率处理单元阳极电源模块的研究

马季军，屈诚志，吴晨昊，石磊磊，吉裕晖

(上海空间电源研究所，上海200245)

1 引言

相比传统化学推进方式，电推进具有比冲高、寿命长、综合性能好等优点，在航天器的推进系统中具有广泛的应用前景。20世纪50年代以来，美国、苏联、德国、英国、日本和中国相继开展了电推进技术的研究。其中，霍尔电推进系统凭借其推力密度大、可靠性好等优势，在卫星和深空探测器上获得了广泛的应用，在执行位置保持和轨道转移等任务时，可以大幅提高航天器的有效载荷重量、寿命以及深空探测距离[1-3]。国际上已有超过10种GEO平台采用了霍尔电推进技术[4-5]。

随着任务需求的不断扩展，大推力成为霍尔电推进系统的主要发展方向[6]。根据能量守恒原理，霍尔电推进系统推力越大，则其供电系统即功率处理单元的功率也就越大。而由于阳极电源功率占功率处理单元的90%以上，大推力也就意味着需要大功率的阳极电源。Bozak等[7]对15 kW、50 kW甚至100 kW以上的功率处理单元都进行了研究，José[8]也进行了20 kW的功率处理单元的研究。国外对于大功率的阳极电源普遍采用多个阳极电源模块串并联来实现，作为整个大功率阳极电源的基石，阳极电源模块也是研究的重点和难点。目前，我国千瓦级的霍尔电推进系统已经充分验证并应用于某些卫星，但是大功率的阳极电源模块的研究依然处于摸索阶段。

本文从功率拓扑、电路仿真等方面对大功率的阳极电源进行研究，并通过试验表明理论分析的可行性和正确性。

2 阳极电源功率拓扑

霍尔电推进阳极电源的难点在于选择合适的功率拓扑，以满足其大功率、多模式的工作特点。首先从功率角度出发，不同的功率拓扑具有不同的适用功率等级，其一般的适用功率如表1所示。

表1 变换拓扑适用场合Table 1 Application occasions of different topologies

由表1可知，对于大功率(几千瓦到几十千瓦级别)的应用，采用全桥拓扑是适合的。而在传统的全桥拓扑中，移相全桥是比较成熟的技术。移相全桥电路拓扑如图1所示。

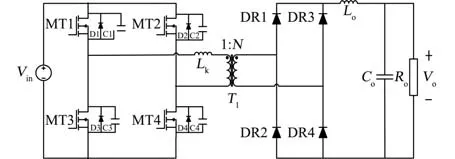
图1 移相全桥电路Fig.1 Phase-shifted full-bridge circuit

通过采用移相控制方式，移相全桥电路可以实现原边开关管的软开关，但是该电路也存在以下缺点：①超前臂实现零电压开关容易，但滞后臂较为困难；②副边占空比丢失严重；③副边整流二极管为硬开关，其两端电压尖峰高、反向恢复问题严重；④整流桥的寄生振荡。为了解决以上问题，赵磊等[9]提出了采用死区时间控制策略来扩展移相全桥零电压开关范围的方法；阮新波等[10-12]提出在原边或副边增加有源或无源电路来实现零电压零电流软开关。以上方法虽然解决移相全桥的部分问题，但是由于本质还是传统的原边移相控制的移相全桥电路，不可避免地会保留一些移相全桥的缺点。而Zhang[13]提出了一种采用副边移相的电路拓扑，这一拓扑相对传统移相全桥拓扑具有以下优点：①原边所有开关管实现零电压开关条件一致，且在全负载范围内都能实现零电压开通；②副边整流二极管自然换流，反向恢复电流小，且其两端电压在关断时被钳位在输出电压上；③由于拓扑特性，相当于在拓扑中嵌入了升压结构，所以具有高的电压增益；④不需要输出滤波电感。即副边移相拓扑具有宽范围的电压增益、软开关能力，并且电路形式简单，因此，采用副边移相电路作为霍尔电推进阳极电源的功率拓扑。

副边移相电路拓扑如图2所示。工作时，MT1、MT4和 MT2、MT3互补导通；MT5相对 MT2移相，MT6相对MT1移相。C1～C6为缓冲电容，D1～D6为功率MOSFET的反并联二极管，DR1、DR2是整流二极管，电感Lk可以是变压器漏感也可以是外加电感。根据电感Lk上电流在开关管(MT1，MT4或 MT2，MT3)关断时的状态，变换器可以工作在连续电流(CCM)模式(关断时Ip≠0)和断续电流(DCM)模式(关断时Ip＝0)。

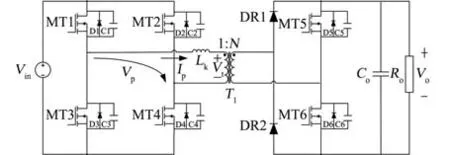
图2 副边移相电路拓扑Fig.2 Topology of secondary phase-shifted circuit

在进行分析之前，为简化分析，先做以下假设：①所有元器件都是理想的；②忽略极间电容；③变压器励磁电感为无穷大；④变换器输出电容足够大，以至于输出电压可以近似认为不变。并定义以下参数：电源电压Vin，电感Lk，电感电流为Ip，变压器变比1∶N，输出电压Vo，定义变换器增益为d＝Vo/N˙Vin。

2.1 CCM模式

CCM模式下的工作波形如图3所示，在一个周期内，共有10种工作状态，由于前后半个周期工作状态类似，所以只需分析前5个状态。

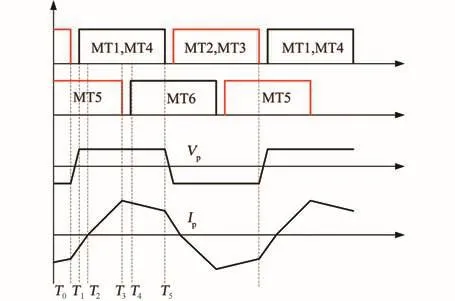
图3 CCM模式工作波形Fig.3 Working waveform of CCM mode

1)模式1：[T0-T1]。在T0时刻之前，电源向负载传输能量，电感电流为负(即与参考方向相反)。在T0时刻，MT2和MT3关断，但关断后电感电流不为0，电感电流将流过MT1、MT4的反并二极管D1、D4。由于反并二极管导通，使得MT1和MT4两端的电压钳位在0，这就为MT1和MT4实现ZVS导通创造了条件。在T1时刻，开关死区时间结束，MT1和MT4导通，模式1结束。时刻t(T0＜t＜T1)，电感电流的值由式(1)所示。

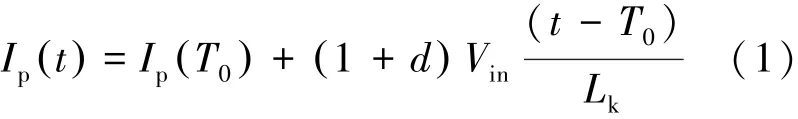
2)模式2：[T1-T2]。T1时刻，MT1和MT4零电压导通，但此时电感电流依然为负，因此，此时电感电流将流过MT1和MT4的沟道。在T2时刻，电感电流增加到0(由负到0)，模式2结束。时刻t(T1＜t＜T2)电感电流依然用公式(1)计算。

3)模式3：[T2-T3]。T2时刻，电感电流Ip到0，流过DR2的电流也为0，因此DR2实现ZCS关断。T2时刻之后，在电源的作用下，电感电流开始正向增加，DR1开始导通，且由于电感电流是从0开始增加的，因此DR1可以ZCS开通。而此时MT5依然导通，所以变压器副边被 MT5和DR1短路，变压器两端电压Vt为0，输入电压直接加在电感Lk上，电感电流Ip线性增加。时刻t(T2＜t＜T3)，电感电流的值由式(2)表示。

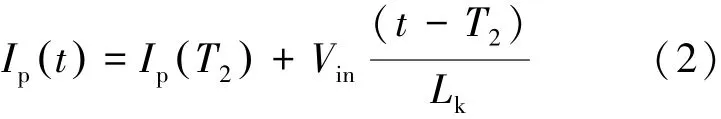
4)模式 4：[T3-T4]。T3时刻，MT5关断，此时电感电流为正，因此，MT6的反并二极管D6导通，将MT6两端电压钳位为 0，从而为 MT6的ZVS开通创造了条件。T4时刻MT6开通，模式4结束。时刻t(T3＜t＜T4)，电感电流的值由公式(3)表示。

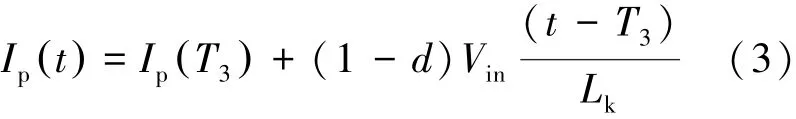
5)模式 5：[T4-T5]。T4时刻，MT6 ZVS开通，此时电感电流依然为正，因此，电流开始流过MT6的沟道。T5时刻，MT1和MT4关断，这一模式结束。时刻t(T4＜t＜T5)，电感电流的值依然可以由式(3)计算。

接下来半个周期的状态与以上5个状态类似。

2.2 DCM模式

由公式(3)可知，当d＞1时，电感电流在T5时刻可以为0，此时电路工作模式将由CCM模式变为DCM模式。在DCM模式下，电路有8个工作状态，如图4所示，且前后半个周期原理一致，分析同CCM模式。

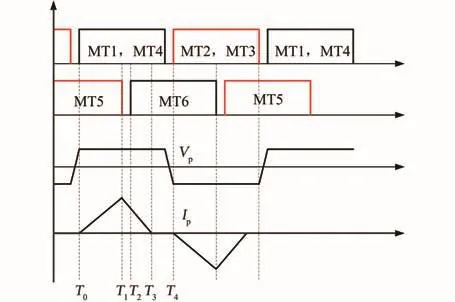
图4 DCM模式工作波形Fig.4 Working waveform of DCM mode

由以上分析可知，在CCM和DCM模式下，开关管的开关特性如表2所示。

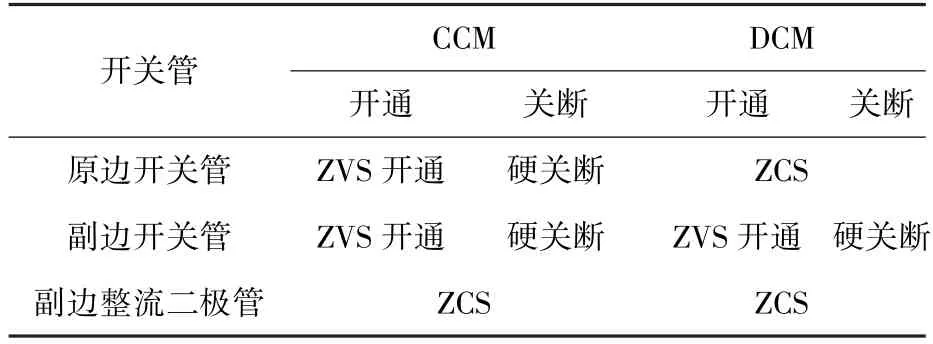
表2 CCM和DCM开关特性Table 2 Switching characteristics of CCM and DCM

即在CCM模式下，原、副边开关管可以实现ZVS开通，副边整流二极管可以实现 ZCS；在DCM模式下，原边开关管和整流二极管可以实现ZCS，副边开关管可以实现ZVS开通。

3 电路仿真

根据第2节的分析与文献[15]可知，拓扑输出功率与原边电感值、驱动移相角存在函数关系，在CCM模式下拓扑传输的能量与原边电感值的关系如式(4)～(6)所示。

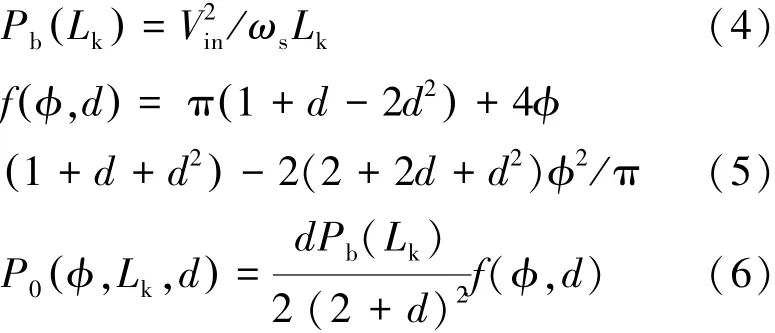
式中：φ为开关管MT6控制信号相对MT1的移相角，Pb(Lk)为归一化功率，f(φ，d)为关于移相角φ和d的函数，ωs为开关角频率。

取d为1，开关频率为25 kHz，可以得到在不同电感值时，输出功率与移相角φ的曲线，如图5所示。由图可知，当输出功率为6500 W，开关频率为25 kHz时，选取原边电感值为5 μH能满足要求。

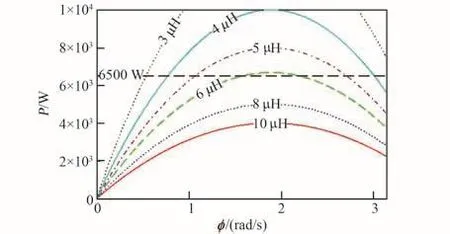
图5 CCM模式输出功率与原边电感、移相角φ的关系曲线Fig.5 Relationship of output power with primary inductance and phase shift angle φ in CCM mode

在DCM模式下，拓扑传输的能量与电感值之间的函数关系如式(7)所示。

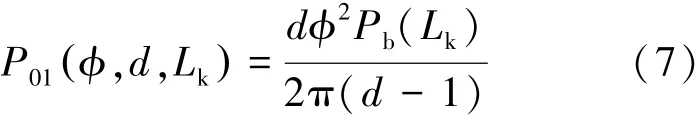
采用Saber仿真软件对副边移相电路进行仿真分析。仿真采用的是理想的MOSFET和变压器模型。仿真参数为输入电压100 V，输出额定功率 6500 W，开关频率 25 kHz，原边电感量5 μH，变压器变比为 1∶3，输出滤波电容 100 μF。

3.1 闭环仿真

闭环仿真的原理图如图6所示，由功率电路(主电路)、反馈控制回路及隔离驱动电路组成。功率电路即副边移相拓扑；反馈控制回路包括电压采样电路、PI调节电路、UC1875移相控制芯片及其外围电路。通过仿真得到输出电压为500 V、输出功率为6500 kW时的电路仿真波形如图7～10所示。图7给出了阳极电源模块的输出电压波形以及原边电感电流波形，由图可知，其输出电压稳定在500 V(out)，原边电感电流I(1，16)的峰值为141.5 A，通过第2节的分析以及图4可知，此时变换器工作在断续模式。图8为原边开关管ZCS开通波形，图中上半部分波形为流过原边某MOS管的电流波形，下半部分为该MOS管DS两端的电压波形(B_ds)以及GS(bg)两端的驱动波形，由图可知，在MOS管驱动上升时，流过MOS管的电流为0，因此此时变换器实现了原边开关管ZCS开通。图9为副边开关管ZVS开通波形，其中F_ds为副边MOS管DS两端电压波形，Fg为其GS两端电压波形，由图可知，在驱动波形上升前(即MOS管开通前)，副边MOS管DS两端的电压已经为0，因此变换器实现了副边开关管ZVS开通。图10为副边整流二极管ZCS波形，由图可知，副边整流二极管每个周期都是从电流为0开始导通，关闭的时候其电流也为0，因此整流二极管ZCS开通以及关断。通过与第2节理论分析对比可知，仿真结果与理论分析一致。

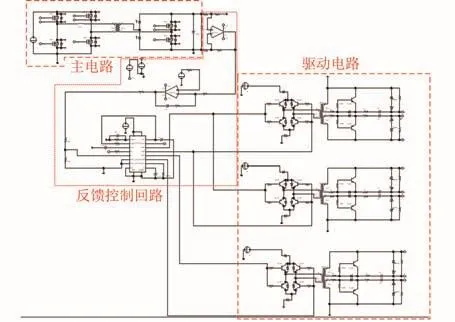
图6 闭环仿真原理图Fig.6 Schematic diagram of closed-loop simulation

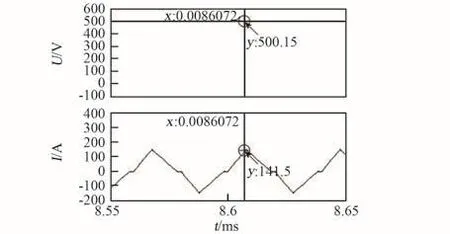
图7 输出电压以及原边电感电流波形Fig.7 Output voltage and primary inductor current waveform

图8 原边开关管ZCS开通波形Fig.8 ZVS turn-on waveform of primary switch

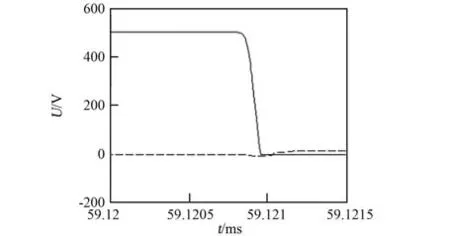
图9 副边开关管ZVS开通波形Fig.9 ZVS turn-on waveform of secondary switch

图10 副边整流二极管ZCS波形Fig.10 ZCS waveform of secondary side rectifier diode

3.2 动态响应

为了分析变换器在切载时的响应，以下对变换器在输出电压为500 V时的负载进行满载—半载—满载切换，负载切换如图 11所示。在30.000 001 ms时切半载，在60.000 001 ms切回满载，输出电压波形如图12所示。由图可知，在切半载时，变换器电压上冲较小，上冲时间也较短；在切满载时，电压下冲较小，下冲时间也较短，说明变换器的动态响应较好。

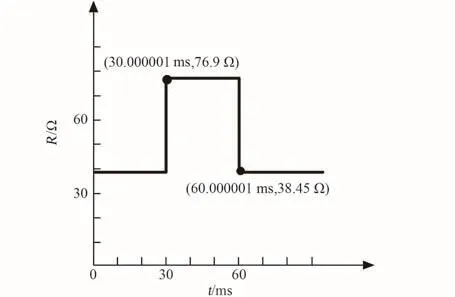
图11 负载切换示意图Fig.11 Diagram of load changing

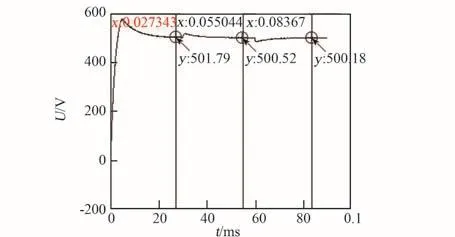
图12 负载切换的输出电压波形Fig.12 Output voltage waveform of load changing

4 试验验证

根据理论计算以及仿真结果绘制原理图及PCB，通过设计调试，研制了一台5 kW的原理样机。原理样机的输入电压为100 V，根据基准设置的不同，其输出电压为300～500 V可调，输出功率为5 kW，试验中以100 V的电源模拟100 V母线，电子负载模拟霍尔推力器特性。当输出电压为350 V时，变换器处于CCM工作模式，其波形如图13～15所示。由图13可知，原边MOS管DS两端电压(绿色波形)在驱动(蓝色波形)开通前就已经下降为 0，因此原边 MOS管为 ZVS开通。由图14可知，副边开关管DS两端电压(蓝色波形)在驱动(绿色波形)开通前也已经下降为0，因此副边MOS管为ZVS开通。由图15可知，通过副边整流二极管的电流在一个周期内从0开始最后下降到0，即副边整流二极管实现了ZCS开通及关断。

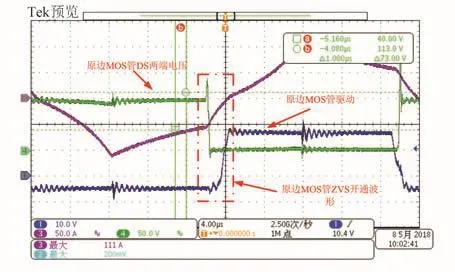
图13 原边开关管ZVS开通波形Fig.13 ZVS turn-on waveform of primary switch

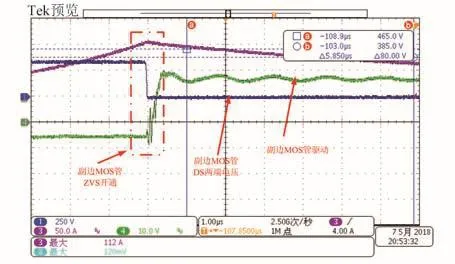
图14 副边开关管ZVS开通波形Fig.14 ZVS turn-on waveform of secondary switch

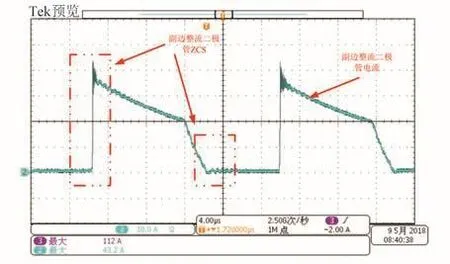
图15 副边整流二极管ZCS波形Fig.15 ZCS waveform of secondary side rectifier diode

由以上分析可知，原理样机实现了原边MOS管的ZVS开通、副边MOS管的ZVS开通以及副边整流二极管的ZCS，与理论、仿真分析一致。但是其电感电流波形并非理论分析中的分段直线，而是分段曲线，这是由于电感是以平均电流值进行设计，但是实际中根据流过电感的电流不同，其感值会略有不同，即电流小时，其电感值较大；电流大时，其电感值较小，从而使得实际的电感电流如图13中紫色波形。

5 结论

1)副边移相电路可以实现原边开关管的ZVS导通、副边开关管的ZVS导通以及副边整流二极管的自然换流，因此电路具有高的变换效率，在大功率的应用中具有明显优势；

2)副边移相电路具有高的电压增益，以及宽范围的软开关能力，能够很好地适应负载范围变化大、具有模式切换要求的霍尔电推进系统；

3)大功率的阳极电源模块的研制成功，意味着可以通过模块串并联组合的方式形成更大功率的阳极电源，进一步提高霍尔电推进供电系统的功率，为未来大推力、高比冲的霍尔电推进系统打好基础。