随机前沿成本模型在医院运行效率的实证分析

屈红雁， 李 芸， 丁 雪， 李纯净

(长春工业大学 数学与统计学院， 吉林 长春 130012)

0 引 言

随机前沿分析法(SFA)是一种新的医院评价方法，是继数据包络分析之后发展起来的,由Aigner[1]在1977年介绍并首次应用在医院评价领域。该方法将随机误差从低效率中分离出来，将误差项(ε)分成两个部分:随机误差(v)和效率残差(u)。随机误差包括观测误差、不可控损耗、时间气候等不可控因素；效率残差包括管理、资源利用和计划制定等方面内容,体现了与最优前沿面的差距,通过效率残差的大小确定机构无效率的程度，可以更加准确地估计出医院的低效率值。SFA包含生产函数和成本函数两种形式，前者研究技术效率，后者主要评价成本效率。对于医院运行效率研究而言，由于随机前沿生产函数要求产出为单一变量,显然不适用于医疗机构的多产出特征[2]。因此，文中对比了带半正态分布的随机前沿成本函数和带截尾正态分布的随机前沿成本函数，给出医院2016—2017年29个科室的运行效率，首次提出某医院评价科室成本效率的方法。

1 随机前沿成本模型在医院临床科室运行效率评价现状

20世纪 70年代末以来,随机前沿方法在生产率分析中得到了广泛应用。为体现前沿技术的随机成分,使测量值更贴近实际的低效率值,国外两个研究小组分别于1977年独自提出了SFA方法。SFA过去在确定性前沿面模型的基础上做了改进,将误差项分成了两个部分,即随机误差和真正反映低效率的残差。中国的生产率分析应用随机前沿生产函数的研究还处于发展阶段，主要集中于对企业行业或地区的经济效率分析，对于该方法在评价临床科室运行效率中的应用尚无文献可查。

医院效益的主体是临床科室。目前国内外已经深入研究了医院整体运行效率的评价体系，对于临床科室的运行效率可追溯到1989年,Eisenberg J M等[3]从经济学角度对临床的投入产出情况做了精辟的论述。国内研究起步于上世纪90年代，文献[4]是关于临床科室运行效率相关的最早研究。近十年来国内临床科室的运行效率评价开始逐渐增多。对医院运行效率的评价有很多种方法，其中数据包络分析法[5]是一种非参数的前沿评价方法，不需要生产和成本函数；还有TOPSIS法，它是一种基于归一化后的原始数据矩阵,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据[6]。

2 随机前沿成本模型原理

2.1 成本函数

成本函数的一般模型

c=c(yi,ωi)eεi。

对成本函数取对数

lnc=ln(yi,ωi)+ui+vi。

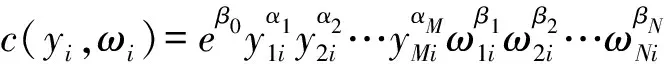
式中：c----全部成本；

y----产出；

ω----投入；

Vi----误差项，独立同分布于正态分布N(0,σ2)，由不可控因素引起，如地震、海啸、疫情等自然灾难或者不可控的天气因素引起；

ui≥0----“无效率”项，相互独立且服从于相同的分布，一般常用的分布有四种：半正态分布、截断正态分布、伽马分布和指数分布。

ui，vi相互独立且分别与yi,ωi独立。令混合扰乱项εi=vi+ui，因为E(εi)=E(vi)+E(ui)=E(ui)≠0，故不能直接使用OLS估计无效率项ui，因此使用极大似然估计对参数进行估计。

ui在不同分布下，参数的极大似然估计：

ui，εi相互独立，其联合密度函数为

则εi的边际密度函数为

对似然函数的各参数求偏导，令其为零，得到各参数的估计值。

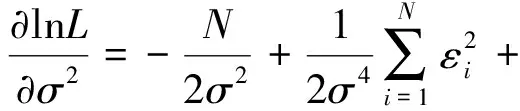
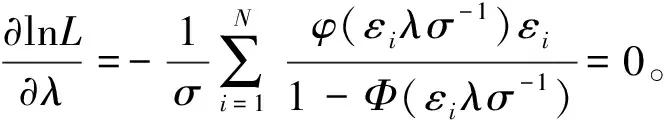
ui，εi相互独立，其联合密度函数为

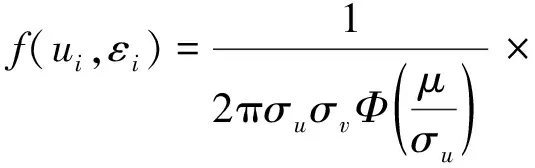
则εi的边际密度函数为

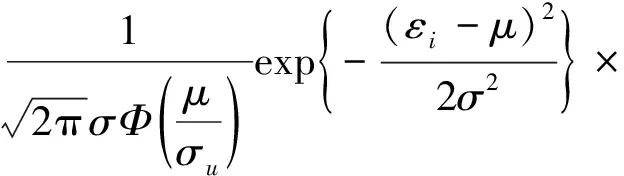
Φ(εiλσ-1+μλ-1σ-1),

其相应的对数似然函数为

对似然函数的各参数求偏导，令其为零，得到各参数的估计值。

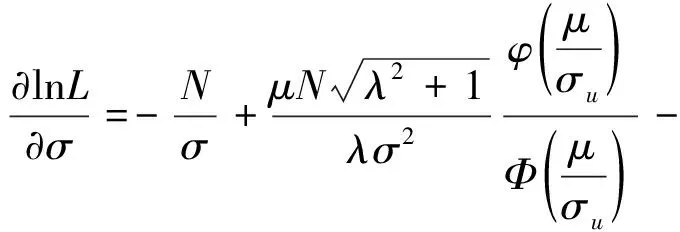
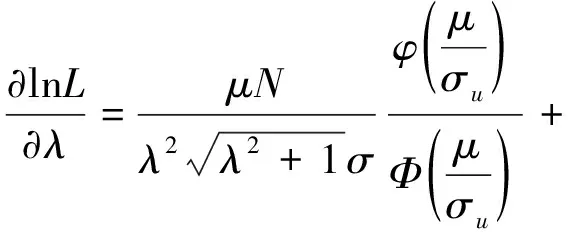
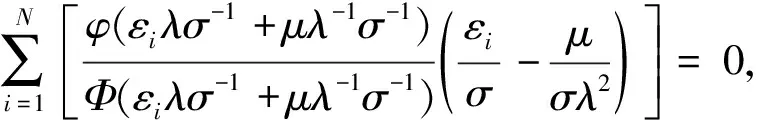
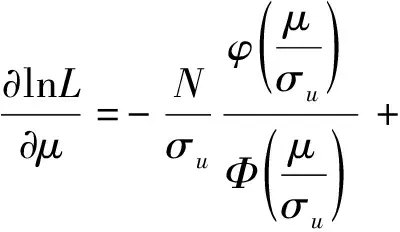
由于直接用方程得到参数的估计值不太容易，所以文中用Frontier 4.1来求解，得到σu和σv的值。ui的分布还可以是指数分布或者伽马分布，因半正态分布计算简单，故使用最多。

2.2 模型的检验

在模型被用于解决实际问题时，要考虑模型是否符合实际，因此需要对模型进行检验。对随机前沿模型的检验主要是似然比检验，检验样本来自何类分布，以下是其检验统计量的构造:

设X=(X1,X2,…,Xn)的密度函数为f(X;θ),其中θ为参数向量,“H0:θ=θ0VSH1:θ=θ1(θ0≠θ1)”。

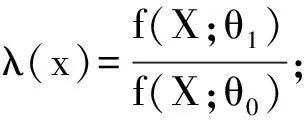
对于随机前沿模型的检验，使用对数似然函数的形式，其检验统计量为

λ(x)=2{ln[f(X;θ1)]-ln[f(X;θ0)]},

λ(x)近似分布为卡方分布，其自由度为约束条件的个数。

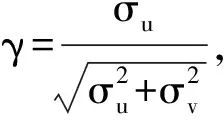
3 实例分析

3.1 数据来源

文中数据来自某医院2014-2017年58个科室的指标数据，包括内科、外科、神经外科等所有科室，指标变量包含每个科室的医务人员、床位数、年出院人次(年诊次)、病床使用率、病床周转次数、平均住院日、手术量、总成本(含医保及管理费用)。其中带有手术量的科室有29个，由于在计算医院科室运行效率时，科室年手术量是一个很重要的指标，它表明了该科室医疗资源利用率的高低，是一个非常重要的产出指标[7]，因此带有手术量的科室在医院具有影响力,且承担繁重医疗服务任务，故文中对带有手术量的29个科室的各项指标数据进行对比分析[8]。

3.2 变量的选择

通过对成本模型的研究，可以得到与医院成本效率相关的四种变量：

总成本变量ci：用医保及管理费用(万元)表示。

产出变量(y)：年门诊人次(y1)，手术量(y2)。

产出特征变量：病床使用率(y3)、病床周转次数(y4)、平均住院日(y5)，它们反映了医院的医疗水平和服务质量。

投入价格要素变量(ω)：床位(ω1)。

3.3 2016年数据结果分析

首先对某医院2016年数据进行处理，对2016年这些指标做统计描述，见表1。

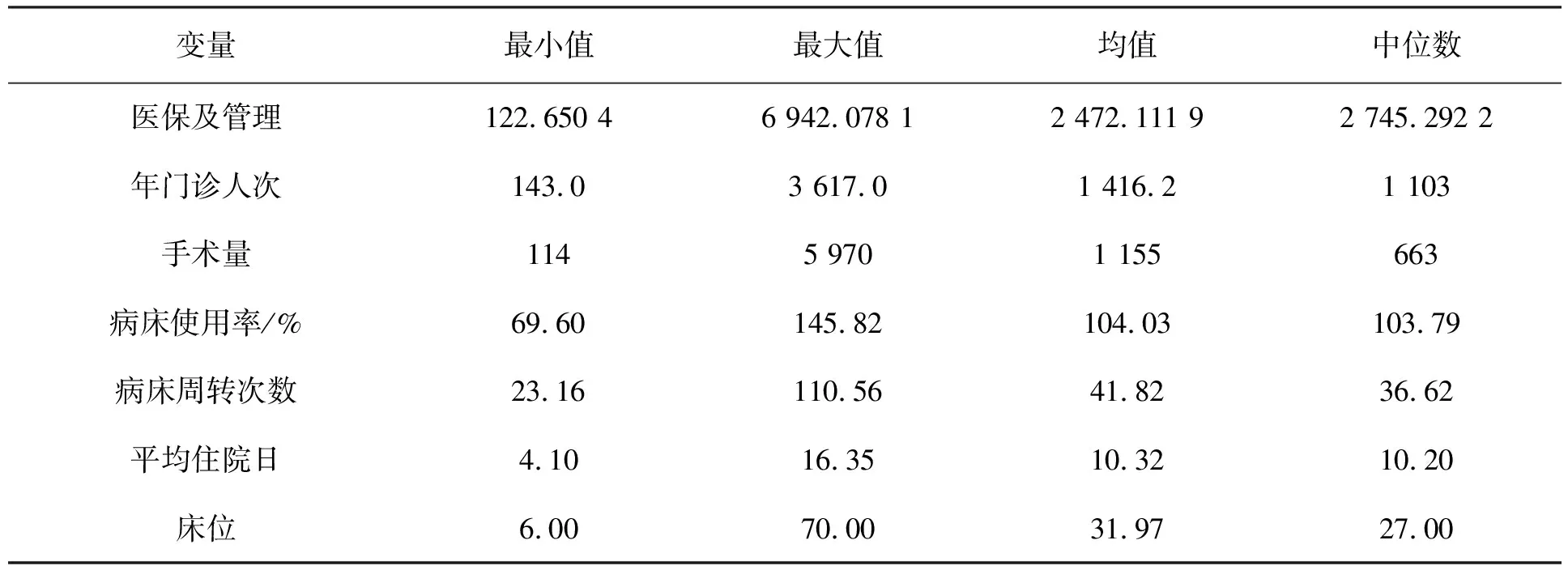
表1 2016年数据统计描述

基于前面对随机前沿成本函数的研究，建立随机前沿成本函数模型为

lnci=β0+β1lny1i+β2lny2i+β3lny3i+

β4lny4i+β5lny5i+β6lnω1i+ui+vi。

运用Frontier 4.1对2016年某医院29个科室的医疗数据做随机前沿成本模型参数估计和假设检验，结果见表2。

表2 参数估计结果

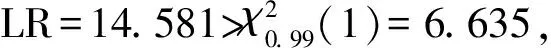
截尾正态分布下每个科室的运行效率有很大差异，其中效率在0.5以上的科室有22个，达到0.9以上的科室有9个，效率在0.5以下的科室有7个，可以看出这29个带有手术量的科室大多都可以合理地利用医疗资源，使最小可达成本与实际成本的比值达到0.5以上，但也存在部分科室的运行效率低下，说明这些科室医疗资源利用不合理，管理方式不恰当，应当给予重视并合理调配医疗资源。效率达到0.9以上的科室见表3。

3.4 2017年数据结果分析

对2017年统计指标数据做统计见表4。

利用frontier 4.1对2017年某医院29个科室的医疗数据做随机前沿成本模型参数估计和假设检验，结果见表5。

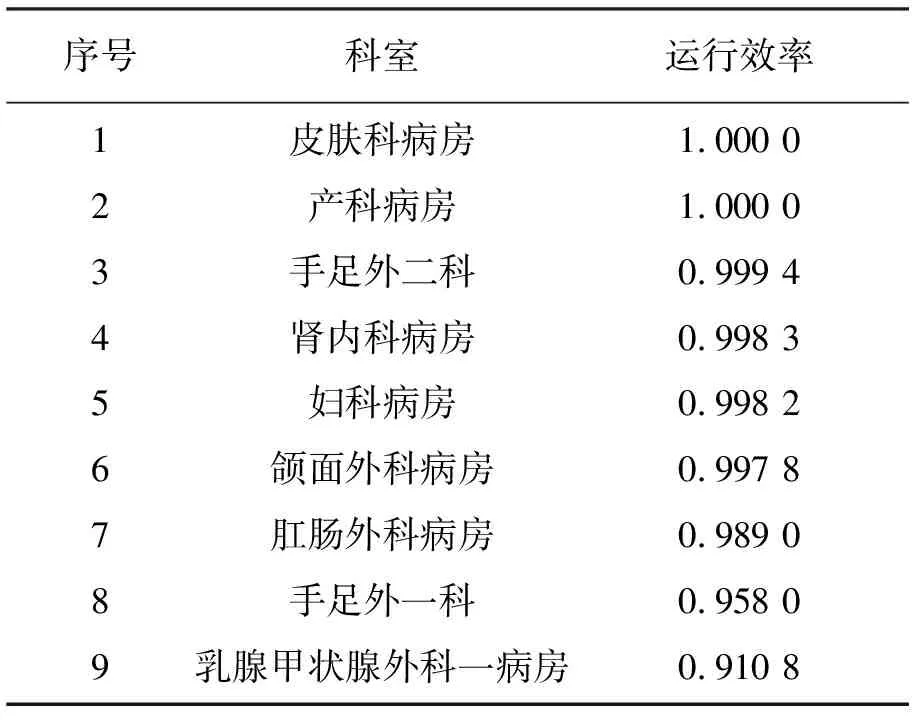
表3 2016年效率0.9以上的科室

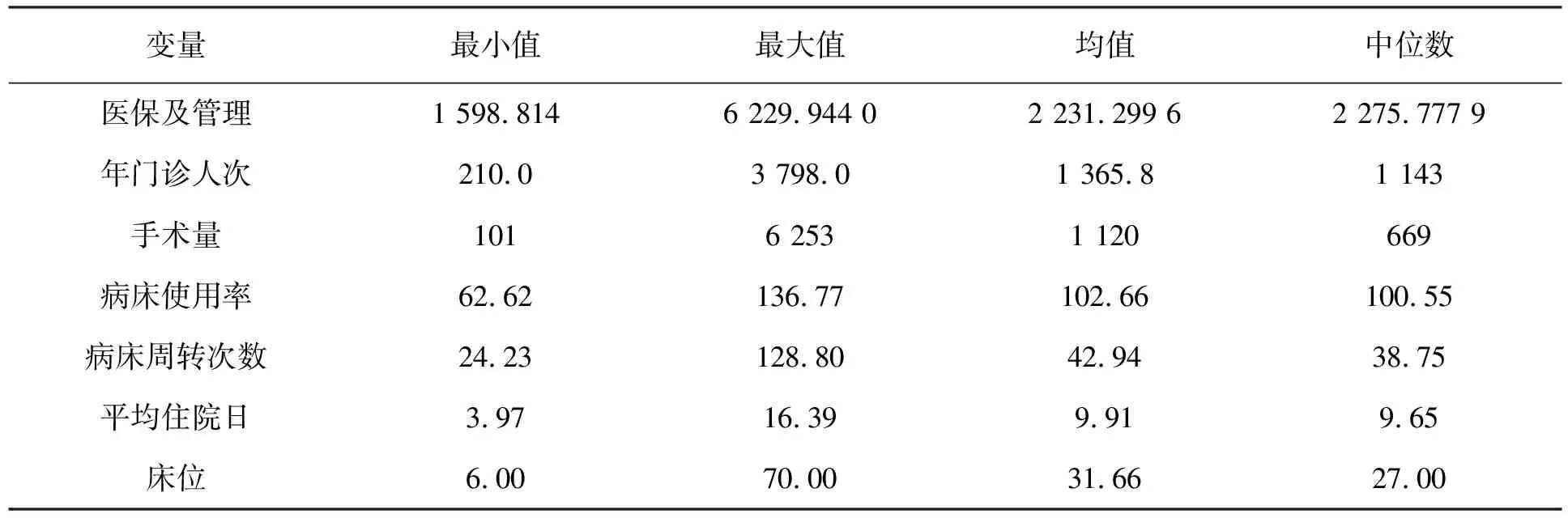
表4 2017年数据统计描述

表5 2017年参数估计结果

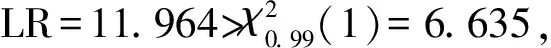
半正态分布下每个科室的运行效率有很大的差异，其中效率在0.5以上的科室有14个，达到0.9以上的科室有6个，效率在0.5以下的科室有15个，可以看出,该医院在2017年整体运行效率都偏低，各科室运行效率也较2016年普遍偏低，其中效率达到0.9以上的科室见表6。

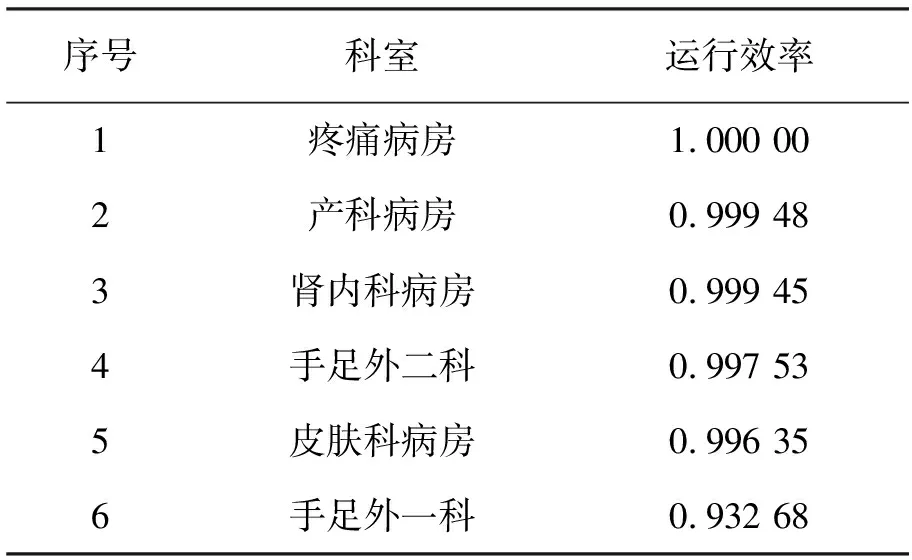
表6 2017年效率0.9以上的科室

4 结 语

对某医院2016年和2017年医疗数据做出分析:

1)当无效率项ui选择半正态分布和截尾正态分布时，所得到的结果大致相同，因此无效率项ui分布的选择对结果不会产生很大影响，所以一般情况下选择半正态分布，因为其计算简单。

2)从运行效率结果来看，2016年医院运行成本效率高于2017年，且2017年都没有达到50%，各科室运行效率较2016年明显降低，即该医院2017年医疗服务和管理水平较2016年偏低，说明医院进行内部改革的第一年可能存在粗放管理和医疗资源利用不足。所以,应当尽快建立完善的管理机制和高效的医疗服务水平，合理分配各科室的医疗资源，以提高医院整体的运行效率。

3)从分析结果看，该省所有综合大型医院都存在科室资源分配不合理的情况，因此对于那些门诊人次过大和需要大量做手术的科室应当给予更大比重的医疗资源配置，那些手术量和门诊人数较少的科室应适当缩减资源配置，使医院总体运行效率达到相对最高，因此该方法对省医疗体系都具有参考价值。